Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
Some asymmetric inequalities
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 359-376
- Print publication:
- July 1950
-
- Article
- Export citation
On fourfolds with canonical curve sections
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 419-428
- Print publication:
- July 1950
-
- Article
- Export citation
The Besicovitch dimension of Cartesian product sets
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 383-386
- Print publication:
- July 1950
-
- Article
- Export citation
The Requirement for Precise Navigation
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 01 July 1950, pp. 219-227
- Print publication:
- July 1950
-
- Article
- Export citation
The distribution of the multiple correlation coefficient
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 521-522
- Print publication:
- July 1950
-
- Article
- Export citation
NAV volume 3 issue 3 Cover and Back matter
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 01 July 1950, p. b1
- Print publication:
- July 1950
-
- Article
-
- You have access
- Export citation
Investigations into the Dip of the Horizon
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 01 July 1950, pp. 270-279
- Print publication:
- July 1950
-
- Article
- Export citation
Zur Verallgemeinerung des Schwarzschen Lemmas auf mehrere Dimensionen
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 396-405
- Print publication:
- July 1950
-
- Article
- Export citation
A New Edition of Myerscough and Hamilton - Rapid Navigation Tables (2nd edition). W. Myerscough and W. Hamilton; Sir Isaac Pitman & Sons, February 1950; 114; cloth; 10·7 × 6·8; 17s 6d.
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 01 July 1950, p. 313
- Print publication:
- July 1950
-
- Article
- Export citation
Some probability distributions connected with recording apparatus. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 429-435
- Print publication:
- July 1950
-
- Article
- Export citation
The lateral diffusion of a cloud of falling droplets
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 500-507
- Print publication:
- July 1950
-
- Article
- Export citation
On Euclid's Algorithm in cubic self-conjugate fields
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 377-382
- Print publication:
- July 1950
-
- Article
- Export citation
The Controller's Viewpoint
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 01 July 1950, pp. 213-218
- Print publication:
- July 1950
-
- Article
- Export citation
Notes on gas flow through a nozzle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 492-499
- Print publication:
- July 1950
-
- Article
- Export citation
The Weather At Sea - Meteorology for Seamen. Commander C. R. Burgess 1950; Brown Son & Ferguson; cloth 8·3 × 5·4 in.; 252 + xi pp., 15s.
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 01 July 1950, pp. 310-313
- Print publication:
- July 1950
-
- Article
- Export citation
Navigation and Strategy in Ocean Racing
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 01 July 1950, pp. 286-302
- Print publication:
- July 1950
-
- Article
- Export citation
The 3-Position Line Problem at Sea
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 01 July 1950, pp. 307-309
- Print publication:
- July 1950
-
- Article
- Export citation
A stable ninety-nine channel pulse amplitude analyser for slow counting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 508-518
- Print publication:
- July 1950
-
- Article
- Export citation
High-speed flow of a gas past an approximately elliptic cylinder
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 479-491
- Print publication:
- July 1950
-
- Article
- Export citation
Microwave Direction Finding for Aircraft Navigation
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 3 / July 1950
- Published online by Cambridge University Press:
- 01 July 1950, pp. 251-269
- Print publication:
- July 1950
-
- Article
- Export citation
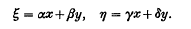
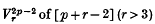 whose generic curve sections are canonical curves of genus
whose generic curve sections are canonical curves of genus 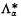 as follows (
as follows (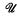 (δ,
(δ, 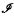 (δ,
(δ, 
