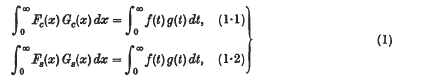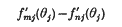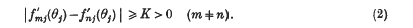Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
NAV volume 3 issue 2 Cover and Front matter
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. f1-f12
- Print publication:
- April 1950
-
- Article
-
- You have access
- Export citation
Biographical Notes on Fellows Elected in 1949
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 194-197
- Print publication:
- April 1950
-
- Article
- Export citation
Institute Notices
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 209
- Print publication:
- April 1950
-
- Article
- Export citation
An improved approximate analytic solution of the Thomas-Fermi equation for atoms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 356-357
- Print publication:
- April 1950
-
- Article
- Export citation
Supersonic flow over an inclined wing of zero aspect ratio
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-315
- Print publication:
- April 1950
-
- Article
- Export citation
The Parseval formulae for monotonic functions. III
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-267
- Print publication:
- April 1950
-
- Article
- Export citation
Note on the motion of liquid near a position of separation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 293-306
- Print publication:
- April 1950
-
- Article
- Export citation
The American Institute
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 198
- Print publication:
- April 1950
-
- Article
- Export citation
Radar and Charts: A discussion following a Report on Admiralty Chart 2649
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 156-165
- Print publication:
- April 1950
-
- Article
- Export citation
Lessons from some Collisions and Groundings at Sea
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 166-182
- Print publication:
- April 1950
-
- Article
- Export citation
The Accuracy Requirements of an En-Route Aid
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 205-206
- Print publication:
- April 1950
-
- Article
-
- You have access
- Export citation
A note on the relativistic invariance of quantized field theories
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 316-318
- Print publication:
- April 1950
-
- Article
- Export citation
PSP volume 46 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1950
-
- Article
-
- You have access
- Export citation
The expected number of aggregates in a random distribution of n points
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 285-292
- Print publication:
- April 1950
-
- Article
- Export citation
The Council
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 197
- Print publication:
- April 1950
-
- Article
- Export citation
Some metrical theorems in Diophantine approximation. III†
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 219-225
- Print publication:
- April 1950
-
- Article
- Export citation
Further results for the counterfeit coin problems
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 226-230
- Print publication:
- April 1950
-
- Article
- Export citation
Star Altitude Curves for High Latitudes
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 199
- Print publication:
- April 1950
-
- Article
- Export citation
A New Gravity Survey
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 198
- Print publication:
- April 1950
-
- Article
- Export citation
A proof of liapounoff's inequality
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, p. 353
- Print publication:
- April 1950
-
- Article
- Export citation