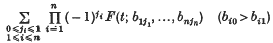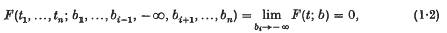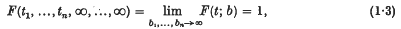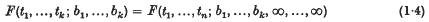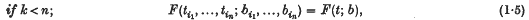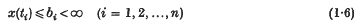Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
Classical statistical mechanics of a rectilinear assembly
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 182-194
- Print publication:
- January 1950
-
- Article
- Export citation
NAV volume 3 issue 1 Back matter
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. b1
- Print publication:
- January 1950
-
- Article
-
- You have access
- Export citation
NAV volume 3 issue 1 Cover and Front matter
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. f1-f10
- Print publication:
- January 1950
-
- Article
-
- You have access
- Export citation
A note on electron theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-201
- Print publication:
- January 1950
-
- Article
- Export citation
PSP volume 46 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1950
-
- Article
-
- You have access
- Export citation
Navigation in High Speed Flight
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 61-78
- Print publication:
- January 1950
-
- Article
- Export citation
The nuclei of non-associative division algebras
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-18
- Print publication:
- January 1950
-
- Article
- Export citation
The use of two Decca chains to obtain accurate fixes at long ranges
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 34-38
- Print publication:
- January 1950
-
- Article
- Export citation
Consol - Radiofaros ‘Consol’. Publicacción Especial Número 2, Instituto Hidrográphico de la Marina, Cadiz, 1949 ; 59 pp.; paper, 9·6 × 6·7 in.; 10 pesetas. - Consol, an Aid to Navigation. M.C.A.P. 59; H. M. Stationery Office, 1948; 16 pp.; paper, 9·8 × 7·2 in.; 1s.
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 99-100
- Print publication:
- January 1950
-
- Article
- Export citation
Committees 1949–1950
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 95
- Print publication:
- January 1950
-
- Article
- Export citation
Grouping corrections and maximum likelihood equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 106-110
- Print publication:
- January 1950
-
- Article
- Export citation
Contributions to the Journal
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 104-105
- Print publication:
- January 1950
-
- Article
- Export citation
The condition of a certain matrix
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 116-118
- Print publication:
- January 1950
-
- Article
- Export citation
On quadrature formulae
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-126
- Print publication:
- January 1950
-
- Article
- Export citation
Institute Notices
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 101-103
- Print publication:
- January 1950
-
- Article
- Export citation
An Elizabethan Compass Maker
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 39-42
- Print publication:
- January 1950
-
- Article
- Export citation
Astronomical Navigation - Astronomy and Navigation. D. H. Sadler; Royal Astronomical Society (Occasional Notes, No. 13); September 1949; 126 pp.; paper 10 × 6·75 in.; 3s. 6d.
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 100
- Print publication:
- January 1950
-
- Article
- Export citation
Radar and the Rule of the Road at Sea
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 10-21
- Print publication:
- January 1950
-
- Article
- Export citation
The definition of measure in function space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-27
- Print publication:
- January 1950
-
- Article
- Export citation
The invariants of a finite collineation group in five dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 73-90
- Print publication:
- January 1950
-
- Article
- Export citation
 .
.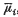 , the grouped population moments, so we require θ as a function of the
, the grouped population moments, so we require θ as a function of the 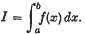 It is, however, often found that even if the analytical expression of
It is, however, often found that even if the analytical expression of