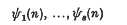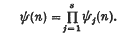Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
PSP volume 46 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1950
-
- Article
-
- You have access
- Export citation
The Altitude-Azimuth Curve - Étude sur une conception nouvelle d'une table de point astronomique. ProfessorP. Hugon; Publication No. 382(d) of the Service Central Hydrographique of the (French) Ministère de la Défense Nationale (Secrétariat d'État chargé de la Marine).
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 203-204
- Print publication:
- April 1950
-
- Article
- Export citation
A National Institute of Oceanography
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 197-198
- Print publication:
- April 1950
-
- Article
- Export citation
Improving the Radar Performance of a Buoy: An analysis of results before and after fitting a reflector
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 183-188
- Print publication:
- April 1950
-
- Article
- Export citation
A Critical Table for Sextant Corrections
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 205
- Print publication:
- April 1950
-
- Article
-
- You have access
- Export citation
A comparison of some absolute methods of measuring fast neutron flux
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 339-352
- Print publication:
- April 1950
-
- Article
- Export citation
On the theory of grand partition functions†
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 319-330
- Print publication:
- April 1950
-
- Article
- Export citation
The Parseval formulae for monotonic functions. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-248
- Print publication:
- April 1950
-
- Article
- Export citation
Some metrical theorems in Diophantine approximation. I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 209-218
- Print publication:
- April 1950
-
- Article
- Export citation
A New Set of Reduction Tables - Kortbestek Tafel by J. C. Lieuwen; being Deel II of Zeevaartkundige Tafels; prepared for the (Dutch) Ministerie van Marine. 's-Gravenhage, 1949; 160, ii; cloth, 11·6 × 8·2 inches; no price stated.
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 200-203
- Print publication:
- April 1950
-
- Article
- Export citation
The oscillatory behaviour of moving averages
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 272-280
- Print publication:
- April 1950
-
- Article
- Export citation
A Survey of Navigation Systems and Instrument Aids
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 141-155
- Print publication:
- April 1950
-
- Article
- Export citation
Aerial Magnetic Survey
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 121-132
- Print publication:
- April 1950
-
- Article
- Export citation
Astro-Fix by Computation
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 107-120
- Print publication:
- April 1950
-
- Article
- Export citation
The Centre Belge de Navigation
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 198
- Print publication:
- April 1950
-
- Article
- Export citation
Probability distributions and orthogonal parameters
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 281-284
- Print publication:
- April 1950
-
- Article
- Export citation
Siting the Radar Scanner
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 2 / April 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 189-193
- Print publication:
- April 1950
-
- Article
- Export citation
Aircraft Radio Altimeters
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 79-89
- Print publication:
- January 1950
-
- Article
- Export citation
Surface waves on deep water in the presence of a submerged circular cylinder. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-158
- Print publication:
- January 1950
-
- Article
- Export citation
PSP volume 46 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1950
-
- Article
-
- You have access
- Export citation