Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
On the existence of metric differential geometries based on the notion of area
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-72
- Print publication:
- January 1950
-
- Article
- Export citation
Annual Dinner 1949
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 95-96
- Print publication:
- January 1950
-
- Article
- Export citation
Numerical integration by systematic sampling
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-115
- Print publication:
- January 1950
-
- Article
- Export citation
Projective mutual invariants of a space cubic and a linear complex
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 195-198
- Print publication:
- January 1950
-
- Article
- Export citation
Rayleigh's problem for a semi-infinite plate
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-140
- Print publication:
- January 1950
-
- Article
- Export citation
The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 159-163
- Print publication:
- January 1950
-
- Article
- Export citation
A note on boundary perturbations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 206-207
- Print publication:
- January 1950
-
- Article
- Export citation
Liverpool Port Radar Station
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 96-97
- Print publication:
- January 1950
-
- Article
- Export citation
Elastic deformations of infinite strips
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 164-181
- Print publication:
- January 1950
-
- Article
- Export citation
A sextic primal in five dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 91-105
- Print publication:
- January 1950
-
- Article
- Export citation
Notes on the secular determinant in molecular orbital theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 202-205
- Print publication:
- January 1950
-
- Article
- Export citation
On the iteration of a continuous mapping of a compact space into itself
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 46-56
- Print publication:
- January 1950
-
- Article
- Export citation
On differentiation and Denjoy-behaviour of functions of two real variables
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 28-45
- Print publication:
- January 1950
-
- Article
- Export citation
The Earth's Magnetic Field
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 1-9
- Print publication:
- January 1950
-
- Article
- Export citation
Admiralty Chart 2649: A Chart Adapted for use with Radar
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 22-33
- Print publication:
- January 1950
-
- Article
- Export citation
Surface waves on deep water in the presence of a submerged circular cylinder. I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 141-152
- Print publication:
- January 1950
-
- Article
- Export citation
Annual General Meeting
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 90-95
- Print publication:
- January 1950
-
- Article
- Export citation
Pressure Pattern Flying - Theoretical Aspects of Pressure-Pattern Flying. J. S. Sawyer; H.M. Stationery Office Meteorological Report No. 3, M.O.496C, October 1949; 64 pages, 24 illustrations; paper 9·6 × 6·0 inches; 1s. 3d.
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 98
- Print publication:
- January 1950
-
- Article
- Export citation
On two theorems of S. Verblunsky
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-66
- Print publication:
- January 1950
-
- Article
- Export citation
An Aircraft Approach Procedure: Some tests with aircraft using Distance Measuring Equipment and the Multiple Track Radar Range
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 1 / January 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 43-60
- Print publication:
- January 1950
-
- Article
- Export citation
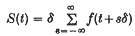
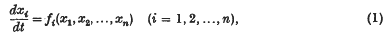
 . As
. As 
