Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
The tabulation of Bessel functions for large argument
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 554-557
- Print publication:
- October 1949
-
- Article
- Export citation
An approximate relation between the energy levels of a particle in a field of given potential energy, calculated on the relativistic and non-relativistic theories
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 631-637
- Print publication:
- October 1949
-
- Article
- Export citation
Elastic stability of infinite strips
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 587-594
- Print publication:
- October 1949
-
- Article
- Export citation
The Kummer quartic and the tetrahedroids based on the Maschke forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 519-535
- Print publication:
- October 1949
-
- Article
- Export citation
Remarks on the Dirac δ-operator
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 489-494
- Print publication:
- October 1949
-
- Article
- Export citation
Discussion
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 308-314
- Print publication:
- October 1949
-
- Article
- Export citation
NAV Volume 2 issue 4 Cover and Front matter
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. f1-f4
- Print publication:
- October 1949
-
- Article
-
- You have access
- Export citation
Axial symmetric stress distributions in aeolotropic hexagonal crystals. The problem of the plane and related problems
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 621-630
- Print publication:
- October 1949
-
- Article
- Export citation
Methods of Plotting and Reduction
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 290-292
- Print publication:
- October 1949
-
- Article
- Export citation
Air Navigation by Zenith-Photography
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 297-304
- Print publication:
- October 1949
-
- Article
- Export citation
The Possibility of an Altitude-Azimuth Almanac for Air Navigation
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 285-289
- Print publication:
- October 1949
-
- Article
- Export citation
On non-linear differential equations of the second order: III. The equation ẍ − k(1 − x2)ẋ + x = p.kλ cos (λt + α), k small and λ near 1.
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 495-501
- Print publication:
- October 1949
-
- Article
- Export citation
Little Ship Navigation - Little Ship Navigation. Lt. Cdr. M. J. Rantzen, R.N.V.R.; Herbert Jenkins, 1949; 164 + xviii; cloth, 8 × 5·2 in.; 12s. 6d. - Pilotage and Navigation for Little Ships. Rev. B. R. Keir Moilliet; Edward Stanford, July 1949; 79 + v; cloth, 7·5 × 5 in.; 7s. 6d. - Navigation without Logarithms. S. de Neufville; Edward Stanford, July 1949; 117 + 95 pp. appendices; cloth, 9.7 × 6·2 in.; 21s. - Offshore. Captain (E.) J. H. Illingworth, R.N.; Robert Ross, July 1949; 236 + xxv, 22 plates, 12 Appendices; cloth, 11 × 8½ in.; 45s.
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 347-349
- Print publication:
- October 1949
-
- Article
- Export citation
Rectilinear flow of non-Bingham plastic solids and non-Newtonian viscous liquids. I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 595-611
- Print publication:
- October 1949
-
- Article
- Export citation
A further inequality in the theory of arithmetic on algebraic varieties
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 510-518
- Print publication:
- October 1949
-
- Article
- Export citation
Proceedings at the meetings held during the session 1948–1949: Annual general meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 684-686
- Print publication:
- October 1949
-
- Article
- Export citation
The cambridge philosophical society statement of accounts for the year ending 31 july 1948
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 687-688
- Print publication:
- October 1949
-
- Article
- Export citation
PSP volume 45 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- October 1949
-
- Article
-
- You have access
- Export citation
An inequality in the theory of arithmetic on algebraic varieties
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 502-509
- Print publication:
- October 1949
-
- Article
- Export citation
A short proof of a theorem on reflexive spaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 4 / October 1949
- Published online by Cambridge University Press:
- 24 October 2008, p. 674
- Print publication:
- October 1949
-
- Article
- Export citation


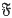
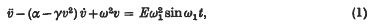

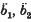 can be neglected, and ḃ
can be neglected, and ḃ