Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
Hyperbolic Projections
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 227-229
- Print publication:
- July 1949
-
- Article
- Export citation
Ionic hydration
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 477-481
- Print publication:
- July 1949
-
- Article
- Export citation
The cardinal series in Hilbert space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 335-341
- Print publication:
- July 1949
-
- Article
- Export citation
Equivalent Head Winds on Air Routes
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 195-209
- Print publication:
- July 1949
-
- Article
- Export citation
Collisions through liquid layers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, p. 488
- Print publication:
- July 1949
-
- Article
-
- You have access
- Export citation
NAV Volume 2 issue 3 Back Matter
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, p. b1
- Print publication:
- July 1949
-
- Article
-
- You have access
- Export citation
The Argentine Nautical Almanac - Almanaque Nautico for the year 1949, prepared by the Observatorio Naval and published by the Ministerio de Marina of the Republica Argentina. 9½ × 8 ins.; 372 pp. + star chart + book-mark + printed end papers; price 8 dollars.
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 269-271
- Print publication:
- July 1949
-
- Article
- Export citation
The Birth of the Compass
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 259-263
- Print publication:
- July 1949
-
- Article
- Export citation
Radar Leading Patterns
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, p. 258
- Print publication:
- July 1949
-
- Article
- Export citation
Note on the geometrical optics of diffracted wave fronts
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 395-404
- Print publication:
- July 1949
-
- Article
- Export citation
Precomputed Altitudes
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 264-265
- Print publication:
- July 1949
-
- Article
- Export citation
I.C.A.O. African-Indian Ocean Region
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, p. 268
- Print publication:
- July 1949
-
- Article
- Export citation
The Compton scattering by particles possessing charge and dipole moment
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 411-428
- Print publication:
- July 1949
-
- Article
- Export citation
On the theory of statistical procedures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 354-359
- Print publication:
- July 1949
-
- Article
- Export citation
The interaction of point particles with charged fields
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 429-440
- Print publication:
- July 1949
-
- Article
- Export citation
On the quantum-mechanical treatment of the optics of crystal lattices
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 452-462
- Print publication:
- July 1949
-
- Article
- Export citation
Magnetic Compass Problems— A Fresh Approach
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. 230-242
- Print publication:
- July 1949
-
- Article
- Export citation
A note on the algebra of S-functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 328-334
- Print publication:
- July 1949
-
- Article
- Export citation
Point-curve correspondences: III. Correspondences on a single surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 45 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 24 October 2008, pp. 342-353
- Print publication:
- July 1949
-
- Article
- Export citation
NAV Volume 2 issue 3 Front matter
-
- Journal:
- The Journal of Navigation / Volume 2 / Issue 3 / July 1949
- Published online by Cambridge University Press:
- 18 January 2010, pp. f1-f4
- Print publication:
- July 1949
-
- Article
-
- You have access
- Export citation
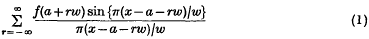
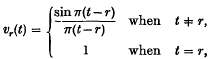
 . Assuming that extraneous energy losses, including any energy imparted to the anvil, are negligible, we may equate this to the energy loss of the hammer
. Assuming that extraneous energy losses, including any energy imparted to the anvil, are negligible, we may equate this to the energy loss of the hammer  . Hence
. Hence