P. 323, line 3 from bottom:

for [8mn−7m−7n+n] read [8mn−7m−7n+4].

P. 328, lines 16 and 18:

for (6mn−6m−6n+l) read (6mn−6m−6n+4).

line 17,

in formula ending … +13m+13n−9) read …+13m+13n−8).

Vol. 43 (1947), pp. 321–8.

Three formalisms have been considered for the ‘extraordinary’ field introduced by Podolsky in his generalized electrodynamics.

The c-representation (tildons) for negative energy particles (§ 3), leads to an unstable vacuum in electron hole theory and must be discarded (§ 7).

The d-representation suggested by Podolsky is a hole theory for bosons. This leads at once to inconsistencies and it is impossible to introduce a Fock representation (§ 6).

The least unsatisfactory is the b-representation (tilde photons) used by PKMG. Tilde photons can be created at high energies but decay immediately by pair creation. The introduction of tilde photons does not interfere with any agreement already established between experiment and ordinary quantum electrodynamics. Evidence might be obtained for the value of the constant a from consideration of the 2S level shift of the hydrogen atom and from the theory of showers where the deviation from the usual theory is greatest (§ 7).

However, the formalism involves the introduction of an indefinite metric for the tilde photon field and consequently ‘negative probabilities’ for states in which an odd number of tilde photons are present. Approximate results can be obtained by assuming that ‘negative probabilities’ in the theory are positive probabilities in the real world. This leads to a small but fundamental error and it does not seem possible that a theory in this form can have any deep seated validity (§ 5).

The same analysis applies to the extension of the Podolsky theory to the Proca field by Green (5). In order that the energy should be positive definite it is necessary to introduce an indefinite metric for one of the two superposed meson fields. Fundamentally the difficulties of interpretation are the same but in practice they will be more obvious because the coupling constants are greater.

1. In a steady two-dimensional motion of viscous liquid in the sharp corner formed by the rigid straight boundaries θ = 0, α, where r, θ are plane polar coordinates, it is found that, near enough to the corner, the most important term in the stream-function is of the form rmf(θ). The index m is evaluated in §§ 2–4 for values of α between 360 and 90°, and is found to be complex if α is less than about 146°; the limiting form of the stream-function when α is small is considered in § 5.

Jet streams are fast moving air streams which appear at times in the levels between 15,000 and 40,000 feet; they are located in the tropical air above the polar front. In this paper examples are given and certain occasions are noted on which they have seriously influenced air navigation.

Early in 1948 when a few charts of the 225 mb. level were drawn to show temperature variations over an air route it was noticed that a very strong stream of air was seen along the line where the tropopause appeared to cut that level. This stream seemed of very considerable length and little width.

A paper under the above title (1) by G. H. Livens was published recently in this journal. The main object of this paper appears to be to show that the treatment of the same subject (2) by myself is unsound. I shall not attempt to refute Professor Livens's opinions. His views concerning magnetic energy have already been criticized by others (3) more expert than myself. I merely wish to draw attention to two completely untrue statements of fact in Professor Livens's paper, namely the following:

(a) On p. 538 “Guggenheim writes therefore

It is trivial that a group all of whose elements except the identity have order two is Abelian; and F. Levi and B. L. van der Waerden(1) have shown that a group all of whose elements except the identity have order three has class less than or equal to three. On the other hand, R. Baer(3) has shown that if the fact that all the elements of a group have orders dividing n implies a limitation on the class of the group, then n is a prime. The object of the present note is to extend this result by showing that if M is a fixed integer there are at most a finite number of prime powers n other than primes, such that the fact that all the elements of a group have orders dividing n implies a limitation on the class of its Mth derived group.

In this paper an investigation is made of the properties of material which is under isotropic stress p when in a strained state, and is such that the relation between the stress and the dilatation Δ is

where α is the density, assumed constant in the unstrained state, and c is the velocity of light. It is shown that in this material the waves of dilatation travel with the velocity of light and that a disk or cylinder composed of this kind of matter suffers no change in radius when it is made to rotate.

It is suggested that it is not unreasonable to attach the label incompressible to matter having these properties.

The three principal tasks of the navigator on an aerial survey expedition are to get to the survey base, to recognize and define the area to be surveyed, and to fly across this area in parallel flight lines so as to photograph it adequately and economically. During the survey, the courses flown, height, speed and the time of day chosen are all influenced by the demands of the camera and of the photogrammetric machines which will produce the map from the air photographs. For this reason it is essential that the navigator, on whose competence during the survey the results will largely depend, should have a proper understanding of photogrammetry, photography and of the basic principles of ground survey. It is true that the crew will include a photographer and that the photogrammetric aspects of the operation will have been considered beforehand by those responsible for briefing the crew; nevertheless there are always unexpected problems which arise in the field and every aspect of the undertaking must be at the fingertips of the navigator who, in the final count, is responsible for the photographic coverage of the area.

The choice of a numerical method for the solution of ordinary differential equations depends on the associated boundary conditions. When all the boundary conditions are specified at one end of the range of integration, one of the well-known step-by-step methods will generally be used, while the method of relaxation is reserved for the case in which boundary conditions are specified at more than one point (1). In the latter, simple but inaccurate finite-difference formulae are used to provide a first approximation to the required solution; this approximation is then used to give an estimate of the errors involved in the use of the inaccurate formulae, and successive corrections are obtained until the full, accurate finite-difference equations are satisfied (1). The same principle is followed in this paper with regard to step-by-step methods, the main difference being the way in which approximate solutions are obtained. In relaxation methods simultaneous equations are solved, while in the use of the step-by-step methods suggested here successive pivotal values are built up by the use of recurrence relations. All the methods of this paper follow this principle, differing only in the method of obtaining a recurrence relation, and consequently in the form of the correction terms.

A quantitative study of the law of force between bubbles floating on a fluid has been made and the results exhibited in the form of a potential energy-distance curve. The main approximations made are that the inclination of the surface of the fluid is small (so that the equations for the surface become linear), and that the submerged portion of the bubble remains spherical. The latter assumption restricts the validity of the results to small bubbles of about 3·0 mm. diameter and less.

One object of the work was to determine the size of bubble which simulated most nearly a typical atomic interaction curve. This application arises in connexion with Prof. Bragg's ‘bubble’ model of crystal lattices. Exact simulation cannot be expected, for the bubble model is two-dimensional, and also does not exert forces analogous either to Coulomb repulsion or to the metallic bond. It can be shown, however, that the law of force between bubbles of a particular size is a remarkably close fit to the law of force between inert gas atoms, that is, to an interaction consisting of a van der Waals attraction and a short-range or ‘overlap’ repulsion. Fig. 4 illustrates this point. The two full curves are the energy-distance curves for krypton and argon atoms (plotted from Fowler, Statistical Mechanics, 2nd ed., Chapter x, Table 29). The circles mark the corresponding curve for bubbles with α = 1·0 (i.e. of diameter 3 mm. in soap solution). The units of energy and distance are chosen so as to bring the minimum of each curve to the point (1, − 50). It will be seen that the curves are remarkably similar over the range shown.

In this paper, it has been shown that the usual demonstrations of the phenomenon of Bose-Einstein condensation are invalid. Exact formal solutions have been derived for the partition functions and the mean occupation numbers in classical and Bose statistics, and the theory of fluctuations in the case of Bose statistics has been given.

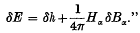
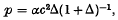
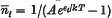In a second paper, convenient approximations will be derived for the mean occupation numbers in Bose statistics, and it will be shown that for temperatures well above the critical temperature of the supposed Bose-Einstein condensation the well-known result for the mean occupation numbers is valid, whilst for temperatures rather lower than this critical value it will be shown that particles will condense into the lowest available state. The critical temperature 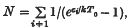T0 is given by where the summation is over all energy levels except the lowest.

Relations are derived between the dose in r./min. delivered by the γ-ray beam from a betasynchrotron and the mean electron current which is incident on the internal target. Comparison with experiment shows that multiple passage of electrons through the target probably plays an important part in production of the γ-ray beam. Some possible effects connected with the multiple passage of electrons are discussed.