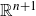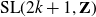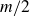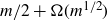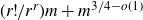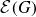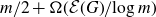Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
On the Aldous-Caputo Spectral Gap Conjecture for Hypergraphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 259-298
- Print publication:
- September 2025
-
- Article
- Export citation
A geometric description of the Reidemeister–Turaev torsion for abelian representations on 3-manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 233-258
- Print publication:
- September 2025
-
- Article
- Export citation
On Thompson groups for Ważewski dendrites
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 189-231
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Chowla conjecture and Landau–Siegel zeroes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 167-187
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Annihilating class groups in p-elementary abelian extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 145-166
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Restricted projections to lines in
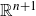 $\mathbb{R}^{n+1}$
$\mathbb{R}^{n+1}$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 105-143
- Print publication:
- July 2025
-
- Article
- Export citation
Uniform sets with few progressions via colourings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 79-103
- Print publication:
- July 2025
-
- Article
- Export citation
Integral Zariski dense surface groups in
 $\textrm{SL}(n,\mathbf{R})$
$\textrm{SL}(n,\mathbf{R})$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 63-78
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost sure upper bound for a model problem for multiplicative chaos in number theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 29-44
- Print publication:
- July 2025
-
- Article
- Export citation
On inhomogeneous Poissonian pair correlations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 17-27
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orbifold Euler characteristics for compactified universal Jacobians over
 $\overline{\mathcal{M}}_{g,\,n}$
$\overline{\mathcal{M}}_{g,\,n}$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-16
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large cuts in hypergraphs via energy
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 45-61
- Print publication:
- July 2025
-
- Article
- Export citation
26 - Dimensional reduction solutions: the domain wall, the cosmic string, and the three-dimensional BTZ black hole solutions
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 286-298
-
- Chapter
- Export citation
33 - Nontrivial topologies: gravitational instantons, Taub–NUT, KK monopole, and Gödel spacetimes
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 362-374
-
- Chapter
- Export citation
27 - Time-dependent gravity solutions: the Friedmann–Lemaître–Robertson– Walker (FLRW) cosmological solution, de Sitter and Anti-de Sitter cosmologies
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 299-310
-
- Chapter
- Export citation
6 - Deflection of light by the Sun and comparison with special relativity
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 64-74
-
- Chapter
- Export citation
References
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 375-380
-
- Chapter
- Export citation
15 - Kerr and Kerr–Newman black hole spacetimes and the Penrose process
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 158-167
-
- Chapter
- Export citation
23 - General relativity solutions and the gauge theory double copy
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 248-260
-
- Chapter
- Export citation
1 - General relativity, kinematics: metric, parallel transport, and general coordinate invariance
-
- Book:
- General Relativity
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 3-17
-
- Chapter
- Export citation