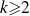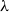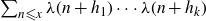1. Introduction
The Liouville function
![]() $\lambda$
is the completely multiplicative function that is defined as
$\lambda$
is the completely multiplicative function that is defined as
![]() $\lambda(n)=(\!-1)^{\Omega(n)}$
for all
$\lambda(n)=(\!-1)^{\Omega(n)}$
for all
![]() $n\in{\mathbb{N}}$
, where
$n\in{\mathbb{N}}$
, where
![]() $\Omega(n)=\sum_{p^{\alpha}\|n}\alpha$
. The prime number theorem implies that
$\Omega(n)=\sum_{p^{\alpha}\|n}\alpha$
. The prime number theorem implies that
which means that the sign of
![]() $\lambda(n)$
has to change frequently as n grows. Chowla expected a more general version of this asymptotic to hold, and in 1965 [
Reference Chowla2
], he stated a conjecture which can be extended to the case of the Liouville function in the following way.
$\lambda(n)$
has to change frequently as n grows. Chowla expected a more general version of this asymptotic to hold, and in 1965 [
Reference Chowla2
], he stated a conjecture which can be extended to the case of the Liouville function in the following way.
Conjecture 1·1. For distinct fixed integers
![]() $h_1, h_2,\ldots, h_k{\geqslant} 0$
, we have that
$h_1, h_2,\ldots, h_k{\geqslant} 0$
, we have that
Chowla’s conjecture remains open till this day. So far, there has only been partial progress on it. Let us now take a look at the the main results that this progress evolved through. In 1985, Harman, Pintz and Wolke [
Reference Harman, Pintz and Wolke4
] studied the binary case with
![]() $h_1=0$
and
$h_1=0$
and
![]() $h_2=1$
and proved that
$h_2=1$
and proved that
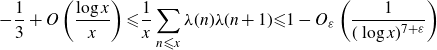 \begin{eqnarray*}-\frac{1}{3} + O\left(\frac{\log{x}}{x}\right) {\leqslant} \frac{1}{x}\sum_{n{\leqslant} x} \lambda(n)\lambda(n+1) {\leqslant} 1 - O_{{\varepsilon}}\left(\frac{1}{(\log x)^{7+{\varepsilon}}}\right)\end{eqnarray*}
\begin{eqnarray*}-\frac{1}{3} + O\left(\frac{\log{x}}{x}\right) {\leqslant} \frac{1}{x}\sum_{n{\leqslant} x} \lambda(n)\lambda(n+1) {\leqslant} 1 - O_{{\varepsilon}}\left(\frac{1}{(\log x)^{7+{\varepsilon}}}\right)\end{eqnarray*}
for
![]() ${\varepsilon} \gt 0$
. About 30 years later, in 2016, Matomäki and Radziwiłł [
Reference Matomäki and Radziwiłł11
, Corollary 2] improved this by showing that for any integer
${\varepsilon} \gt 0$
. About 30 years later, in 2016, Matomäki and Radziwiłł [
Reference Matomäki and Radziwiłł11
, Corollary 2] improved this by showing that for any integer
![]() $h {\geqslant} 1$
, there exists
$h {\geqslant} 1$
, there exists
![]() $\delta(h) \gt 0$
such that
$\delta(h) \gt 0$
such that
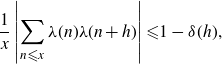 \begin{eqnarray*}\frac{1}{x}\left|\sum_{n {\leqslant} x}\lambda(n)\lambda(n+h)\right| {\leqslant} 1 - \delta(h),\end{eqnarray*}
\begin{eqnarray*}\frac{1}{x}\left|\sum_{n {\leqslant} x}\lambda(n)\lambda(n+h)\right| {\leqslant} 1 - \delta(h),\end{eqnarray*}
for all sufficiently large x. An averaged version of the conjecture was established by Matomäki, Radziwiłł and Tao [
Reference Matomäki, Radziwiłł and Tao12
] in 2015. The three of them proved [
Reference Matomäki, Radziwiłł and Tao12
, (1·3)] that for every integer
![]() $k {\geqslant} 2$
and
$k {\geqslant} 2$
and
![]() $H\in[10,x]$
, we have
$H\in[10,x]$
, we have
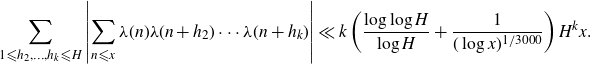 \begin{eqnarray*}\sum_{1{\leqslant} h_2,\ldots,h_k{\leqslant} H}\left| \sum_{n {\leqslant} x} \lambda(n)\lambda(n+h_2)\cdots\lambda(n+h_k) \right| \ll k\left(\frac{\log\log{H}}{\log{H}}+\frac{1}{(\log x)^{1/3000}}\right)H^kx.\end{eqnarray*}
\begin{eqnarray*}\sum_{1{\leqslant} h_2,\ldots,h_k{\leqslant} H}\left| \sum_{n {\leqslant} x} \lambda(n)\lambda(n+h_2)\cdots\lambda(n+h_k) \right| \ll k\left(\frac{\log\log{H}}{\log{H}}+\frac{1}{(\log x)^{1/3000}}\right)H^kx.\end{eqnarray*}
Finally, a weaker version of Chowla’s conjecture, the so-called logarithmically averaged Chowla conjecture which claims that
 \begin{eqnarray*}\sum_{n {\leqslant} x} \frac{\lambda(n+h_1)\cdots\lambda(n+h_k)}{n} = o(\log{x}),\quad \textrm{ as } x \to \infty,\end{eqnarray*}
\begin{eqnarray*}\sum_{n {\leqslant} x} \frac{\lambda(n+h_1)\cdots\lambda(n+h_k)}{n} = o(\log{x}),\quad \textrm{ as } x \to \infty,\end{eqnarray*}
has been accomplished in stages for odd k and
![]() $k=2$
in the works of Tao [
Reference Tao16
], Tao and Teräväinen [
Reference Tao and Teräväinen17
,
Reference Tao and Teräväinen18
], Helfgott and Radziwiłł [
Reference Helfgott and Radziwiłł6
], and Pilatte [
Reference Pilatte13
].
$k=2$
in the works of Tao [
Reference Tao16
], Tao and Teräväinen [
Reference Tao and Teräväinen17
,
Reference Tao and Teräväinen18
], Helfgott and Radziwiłł [
Reference Helfgott and Radziwiłł6
], and Pilatte [
Reference Pilatte13
].
Despite the aforementioned partial advances towards Chowla’s conjecture, the full conjecture still seems to be out of reach. So, one may wish to approach it conditionally, and in this paper, we are doing this by assuming the existence of Landau–Siegel zeroes.
A Landau–Siegel zero, often just called a Siegel zero, is a real number
![]() $\beta$
associated to a real primitive Dirichlet character
$\beta$
associated to a real primitive Dirichlet character
![]() $\chi$
modulo q such that
$\chi$
modulo q such that
![]() $L(\beta,\chi)=0$
and
$L(\beta,\chi)=0$
and
for some
![]() $\eta\gt0$
. The number
$\eta\gt0$
. The number
![]() $\eta$
is called the quality of the Landau–Siegel zero
$\eta$
is called the quality of the Landau–Siegel zero
![]() $\beta$
and from Siegel’s theorem we have the ineffective bound
$\beta$
and from Siegel’s theorem we have the ineffective bound
for any
![]() ${\varepsilon}\gt0$
. It is widely believed that Siegel zeroes do not exist, as their existence would come in contrast to the Generalised Riemann Hypothesis. However, the unlikely presence of Siegel zeroes has proven to have some interesting consequences. For example, in 1983, Heath-Brown [
Reference Heath-Brown5
] proved that if there exist infinitely many Siegel zeroes
${\varepsilon}\gt0$
. It is widely believed that Siegel zeroes do not exist, as their existence would come in contrast to the Generalised Riemann Hypothesis. However, the unlikely presence of Siegel zeroes has proven to have some interesting consequences. For example, in 1983, Heath-Brown [
Reference Heath-Brown5
] proved that if there exist infinitely many Siegel zeroes
![]() $\beta_j=1-1/(\eta_j\log q_j)$
such that
$\beta_j=1-1/(\eta_j\log q_j)$
such that
![]() $\eta_j\to +\infty$
, then the Twin Prime Conjecture must be true.
$\eta_j\to +\infty$
, then the Twin Prime Conjecture must be true.
The first result of the literature on Chowla’s conjecture under Landau–Siegel zeroes comes from a work of Germán and Kátai from 2010. More precisely, in [
Reference Germán and Kátai3
, Theorem 2], they proved that there exists an absolute constant
![]() $c\gt0$
such that if
$c\gt0$
such that if
![]() $\chi$
is a primitive quadratic character modulo q for which
$\chi$
is a primitive quadratic character modulo q for which
![]() $L(\cdot,\chi)$
has a Landau–Siegel zero
$L(\cdot,\chi)$
has a Landau–Siegel zero
![]() $\beta = 1 - 1/(\eta\log{q})$
with
$\beta = 1 - 1/(\eta\log{q})$
with
![]() $\eta \gt \exp(\exp(30))$
, then
$\eta \gt \exp(\exp(30))$
, then
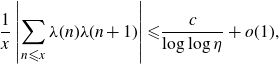 \begin{eqnarray*}\frac{1}{x}\left|\sum_{n {\leqslant} x} \lambda(n)\lambda(n+1)\right| {\leqslant} \frac{c}{\log\log{\eta}}+o(1),\end{eqnarray*}
\begin{eqnarray*}\frac{1}{x}\left|\sum_{n {\leqslant} x} \lambda(n)\lambda(n+1)\right| {\leqslant} \frac{c}{\log\log{\eta}}+o(1),\end{eqnarray*}
for all
![]() $x\in[q^{10},q^{(\log\log{\eta})/3}]$
. Under the same assumptions, Chinis [
Reference Chinis1
, Theorem 1·2] in 2021 extended the work of Germán and Kátai to
$x\in[q^{10},q^{(\log\log{\eta})/3}]$
. Under the same assumptions, Chinis [
Reference Chinis1
, Theorem 1·2] in 2021 extended the work of Germán and Kátai to
![]() $k{\geqslant} 2$
distinct shifts and showed that
$k{\geqslant} 2$
distinct shifts and showed that
for all
![]() $x\in[q^{10},q^{(\log\log{\eta})/3}]$
. A year later, in 2022, Tao and Teräväinen [
Reference Tao and Teräväinen19
, Corollary 1·8 (ii)] improved the bound of Chinis as well as the q-range of x that his bound holds for. In particular, under the existence of a Siegel zero
$x\in[q^{10},q^{(\log\log{\eta})/3}]$
. A year later, in 2022, Tao and Teräväinen [
Reference Tao and Teräväinen19
, Corollary 1·8 (ii)] improved the bound of Chinis as well as the q-range of x that his bound holds for. In particular, under the existence of a Siegel zero
![]() $\beta=1-1/(\eta\log q)$
with
$\beta=1-1/(\eta\log q)$
with
![]() $\eta{\geqslant} 10$
, they showed that for a fixed
$\eta{\geqslant} 10$
, they showed that for a fixed
![]() ${\varepsilon}\in(0,1)$
, one has
${\varepsilon}\in(0,1)$
, one has
for all x in
![]() $[q^{1/2+{\varepsilon}},q^{\eta^{1/2}}]$
. Until the publication of the present paper, the result of Tao and Teräväinen has provided the best bound on the sums
$[q^{1/2+{\varepsilon}},q^{\eta^{1/2}}]$
. Until the publication of the present paper, the result of Tao and Teräväinen has provided the best bound on the sums
![]() $\sum_{n{\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k)$
with the best q-range for x.
$\sum_{n{\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k)$
with the best q-range for x.
In this work, we improve their result in both directions. As we can see in Corollary 1·3 below, the following theorem, which is our main result, leads to stronger bounds on the k-point correlations
![]() $\sum_{n{\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k)$
over a slightly wider q-range.
$\sum_{n{\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k)$
over a slightly wider q-range.
Theorem 1·2. Let
![]() $q{\geqslant} 2$
be a positive integer and let
$q{\geqslant} 2$
be a positive integer and let
![]() $\chi$
be a primitive quadratic character modulo q such that
$\chi$
be a primitive quadratic character modulo q such that
![]() $L(\cdot,\chi)$
has a real zero
$L(\cdot,\chi)$
has a real zero
![]() $\beta = 1 - 1/(\eta\log{q})$
with
$\beta = 1 - 1/(\eta\log{q})$
with
![]() $\eta {\geqslant} 10$
. We also fix an integer
$\eta {\geqslant} 10$
. We also fix an integer
![]() $k{\geqslant} 2$
, distinct non-negative integers
$k{\geqslant} 2$
, distinct non-negative integers
![]() $h_1,\ldots,h_k$
, and
$h_1,\ldots,h_k$
, and
![]() ${\varepsilon}\in(0,1/2)$
. There exists a constant
${\varepsilon}\in(0,1/2)$
. There exists a constant
![]() $c=c({\varepsilon},k)\gt0$
such that for
$c=c({\varepsilon},k)\gt0$
such that for
![]() $x=q^V$
with
$x=q^V$
with
![]() $V\in[1/2+{\varepsilon},\eta]$
, we have
$V\in[1/2+{\varepsilon},\eta]$
, we have
Corollary 1·3. Let
![]() $q, \eta, k$
and
$q, \eta, k$
and
![]() ${\varepsilon}$
be as in the statement of Theorem 1·2. Let also c be the constant from the bound of Theorem 1·2 and consider distinct fixed integers
${\varepsilon}$
be as in the statement of Theorem 1·2. Let also c be the constant from the bound of Theorem 1·2 and consider distinct fixed integers
![]() $h_1,\ldots,h_k{\geqslant} 0$
.
$h_1,\ldots,h_k{\geqslant} 0$
.
-
(i) There exists a constant
 $c'=c'({\varepsilon},k)\gt 0$
such that for every
$c'=c'({\varepsilon},k)\gt 0$
such that for every \begin{eqnarray*}\sum_{n{\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k) \ll x\exp(\!-c'\sqrt{\log{\eta}}),\end{eqnarray*}
\begin{eqnarray*}\sum_{n{\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k) \ll x\exp(\!-c'\sqrt{\log{\eta}}),\end{eqnarray*}
 $x \in [q^{1/2+{\varepsilon}},q^{c^{-2}\log{\eta}}]$
.
$x \in [q^{1/2+{\varepsilon}},q^{c^{-2}\log{\eta}}]$
.
-
(ii) For every
 $\delta\in(0,1)$
, we have that for all
$\delta\in(0,1)$
, we have that for all \begin{eqnarray*}\sum_{n{\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k) \ll_{\delta} \frac{x}{\eta^{1-\delta}},\end{eqnarray*}
\begin{eqnarray*}\sum_{n{\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k) \ll_{\delta} \frac{x}{\eta^{1-\delta}},\end{eqnarray*}
 $x \in (q^{c^{-2}\log{\eta}},q^{\eta^{\delta}}]$
.
$x \in (q^{c^{-2}\log{\eta}},q^{\eta^{\delta}}]$
.
The implicit constants in Theorem 1·2 and 1·3 depend on
![]() ${\varepsilon},k$
and the shifts
${\varepsilon},k$
and the shifts
![]() $h_1,\ldots,h_k$
, but we did not include them in the
$h_1,\ldots,h_k$
, but we did not include them in the
![]() $\ll$
notation because the parameters
$\ll$
notation because the parameters
![]() ${\varepsilon},k,h_1,\ldots,h_k$
are all fixed in their statements. The same applies to the bounds in the proof of Theorem 1·2. The reason for this choice is to alleviate the notation for the reader.
${\varepsilon},k,h_1,\ldots,h_k$
are all fixed in their statements. The same applies to the bounds in the proof of Theorem 1·2. The reason for this choice is to alleviate the notation for the reader.
We prove Theorem 1·2 in Section 5. A major input in its proof is Lemma 3·3 which is a technical version of the fundamental lemma of sieve theory. Tao and Teräväinen did not use the beta-sieve which basically gives rise to Lemma 3·3. They used a Selberg sieve and this technically complicated the matters in their paper [ Reference Tao and Teräväinen19 ]. This constitutes the main reason that we could improve their bound. However, it could be possible to somehow alter their arguments and obtain bounds comparable to ours with a Selberg sieve.
The use of Lemma 3·3 as a main component in the improvement of the previous results was inspired by the work of Matomäki and Merikoski in [
Reference Matomäki and Merikoski10
], where they assumed the existence of Siegel zeroes and refined a result of Tao and Teräväinen [
Reference Tao and Teräväinen19
] on the binary “Hardy–Littlewood” type correlations
![]() $\sum_{n{\leqslant} x}\Lambda(n)\Lambda(n+h)$
. As in our paper, Matomäki and Merikoski, who were the ones who proved [
Reference Matomäki and Merikoski10
, Lemma 3·3], strengthened the result of Tao and Teräväinen by applying Lemma 3·3 instead of a Selberg sieve that the latter used for the more general “Hardy–Littlewood–Chowla” type correlations
$\sum_{n{\leqslant} x}\Lambda(n)\Lambda(n+h)$
. As in our paper, Matomäki and Merikoski, who were the ones who proved [
Reference Matomäki and Merikoski10
, Lemma 3·3], strengthened the result of Tao and Teräväinen by applying Lemma 3·3 instead of a Selberg sieve that the latter used for the more general “Hardy–Littlewood–Chowla” type correlations
Notation
Let r be a positive integer. For
![]() $a_1,\ldots,a_r\in{\mathbb{N}}$
, we use the notation
$a_1,\ldots,a_r\in{\mathbb{N}}$
, we use the notation
![]() $(a_1,\ldots,a_r)$
for their greatest common divisor, and the notation
$(a_1,\ldots,a_r)$
for their greatest common divisor, and the notation
![]() $[a_1,\ldots,a_r]$
for their least common multiple.
$[a_1,\ldots,a_r]$
for their least common multiple.
Throughout the text, we denote the largest and smallest prime factor of an integer
![]() $n\gt 1$
by
$n\gt 1$
by
![]() $P^+(n)$
and
$P^+(n)$
and
![]() $P^-(n)$
, respectively. For
$P^-(n)$
, respectively. For
![]() $n=1$
, we conventionally have
$n=1$
, we conventionally have
![]() $P^+(1)=0$
and
$P^+(1)=0$
and
![]() $P^-(1)=+\infty$
.
$P^-(1)=+\infty$
.
The capital Greek letters
![]() $\Phi$
and
$\Phi$
and
![]() $\Psi$
also appear in the paper and they correspond to the classical counting functions of the rough and smooth integers, respectively. More precisely, for
$\Psi$
also appear in the paper and they correspond to the classical counting functions of the rough and smooth integers, respectively. More precisely, for
![]() $x{\geqslant} y{\geqslant} 2$
, we have
$x{\geqslant} y{\geqslant} 2$
, we have
![]() $\Phi(x,y)=\#\{n{\leqslant} x\,:\, P^-(n)\gt y\}$
and
$\Phi(x,y)=\#\{n{\leqslant} x\,:\, P^-(n)\gt y\}$
and
![]() $\Psi(x,y)=\#\{n{\leqslant} x\,:\, P^+(n){\leqslant} y\}$
.
$\Psi(x,y)=\#\{n{\leqslant} x\,:\, P^+(n){\leqslant} y\}$
.
Given two arithmetic functions f and g, their Dirichlet convolution, denoted by
![]() $f\ast g$
, is the arithmetic function which is defined as
$f\ast g$
, is the arithmetic function which is defined as
![]() $(f\ast g)(n)=\sum_{ab=n}f(a)g(b)$
for all
$(f\ast g)(n)=\sum_{ab=n}f(a)g(b)$
for all
![]() $n\in{\mathbb{N}}$
.
$n\in{\mathbb{N}}$
.
For
![]() $m\in{\mathbb{N}}$
, the symbol
$m\in{\mathbb{N}}$
, the symbol
![]() $\tau_m$
denotes the m-fold divisor function given as
$\tau_m$
denotes the m-fold divisor function given as
![]() $\tau_m(n)=\sum_{d_1\ldots d_m=n}1$
for all
$\tau_m(n)=\sum_{d_1\ldots d_m=n}1$
for all
![]() $n\in{\mathbb{N}}$
. Finally, the lowercase Greek letters
$n\in{\mathbb{N}}$
. Finally, the lowercase Greek letters
![]() $\mu,\tau$
and
$\mu,\tau$
and
![]() $\varphi$
denote the Möbius, the divisor and the Euler functions, respectively.
$\varphi$
denote the Möbius, the divisor and the Euler functions, respectively.
2. The Core Ideas
The purpose of this section is to explain why the existence of Siegel zeroes is a useful hypothesis when approaching Chowla’s conjecture. Our explanation below also highlights the main steps in the proof of Theorem 1·2.
If
![]() $L(\cdot,\chi)$
has a zero close to 1 for some Dirichlet character
$L(\cdot,\chi)$
has a zero close to 1 for some Dirichlet character
![]() $\chi$
of modulus q, then
$\chi$
of modulus q, then
![]() $L(1,\chi)$
will be small by continuity. Consequently, assuming that Landau–Siegel zeroes exist, we find a primitive quadratic character
$L(1,\chi)$
will be small by continuity. Consequently, assuming that Landau–Siegel zeroes exist, we find a primitive quadratic character
![]() $\chi$
such that
$\chi$
such that
![]() $L(\beta,\chi)=0$
for some real number
$L(\beta,\chi)=0$
for some real number
![]() $\beta$
close to 1. Then
$\beta$
close to 1. Then
![]() $L(1,\chi)^{-1}$
should be large. But,
$L(1,\chi)^{-1}$
should be large. But,
so the Euler product of the right-hand side has to be large, too. In conjunction with Mertens’ theorems, this suggests that
![]() $\chi(p)=-1=\lambda(p)$
for many large primes. This intuitive conclusion is the basis of arguments that utilise the presence of Landau–Siegel zeroes.
$\chi(p)=-1=\lambda(p)$
for many large primes. This intuitive conclusion is the basis of arguments that utilise the presence of Landau–Siegel zeroes.
Now, let
![]() $z\gt 1$
be some parameter. Following the work of Germán and Kátai [
Reference Germán and Kátai3
], we define the completely multiplicative function
$z\gt 1$
be some parameter. Following the work of Germán and Kátai [
Reference Germán and Kátai3
], we define the completely multiplicative function
![]() $\lambda_z$
which is fully determined by its prime values
$\lambda_z$
which is fully determined by its prime values
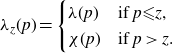 \begin{eqnarray}\lambda_z(p)=\begin{cases}\lambda(p) &\text{if}\ p{\leqslant} z,\\\chi(p) &\text{if}\ p\gt z.\end{cases}\end{eqnarray}
\begin{eqnarray}\lambda_z(p)=\begin{cases}\lambda(p) &\text{if}\ p{\leqslant} z,\\\chi(p) &\text{if}\ p\gt z.\end{cases}\end{eqnarray}
According to the above discussion, in the presence of Siegel zeroes, the function
![]() $\lambda_z$
seems to be a good approximation to the Liouville function
$\lambda_z$
seems to be a good approximation to the Liouville function
![]() $\lambda$
for large z. Therefore, for a suitably chosen z, e.g. some small power of x, we expect
$\lambda$
for large z. Therefore, for a suitably chosen z, e.g. some small power of x, we expect
In fact, such an approximation is provided by Lemma 4·1 which constitutes the first step in the proof of Theorem 1·2.
Once the transition from the sums of
![]() $\lambda$
to the sums of
$\lambda$
to the sums of
![]() $\lambda_z$
has been achieved with the introduction of an acceptable error, the study of the sums
$\lambda_z$
has been achieved with the introduction of an acceptable error, the study of the sums
![]() $\sum_{n{\leqslant} x}\lambda_z(n+h_1)\ldots\lambda_z(n+h_k)$
is tractable. Let us elaborate on why is that. Without loss of generality, we assume that
$\sum_{n{\leqslant} x}\lambda_z(n+h_1)\ldots\lambda_z(n+h_k)$
is tractable. Let us elaborate on why is that. Without loss of generality, we assume that
![]() $h_1$
is the smallest shift. Then the right-hand side of (2·3) can be written as
$h_1$
is the smallest shift. Then the right-hand side of (2·3) can be written as
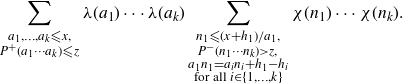 \begin{eqnarray}\sum_{\substack{a_1,\ldots,a_k{\leqslant} x,\\P^+(a_1\cdots a_k){\leqslant} z}}\lambda(a_1)\cdots\lambda(a_k)\sum_{\substack{n_1{\leqslant} (x+h_1)/a_1,\\P^-(n_1\cdots n_k)\gt z,\\a_1n_1=a_in_i+h_1-h_i\\ \text{for all}\ i\in\{1,\ldots,k\}}}\chi(n_1)\cdots\chi(n_k).\end{eqnarray}
\begin{eqnarray}\sum_{\substack{a_1,\ldots,a_k{\leqslant} x,\\P^+(a_1\cdots a_k){\leqslant} z}}\lambda(a_1)\cdots\lambda(a_k)\sum_{\substack{n_1{\leqslant} (x+h_1)/a_1,\\P^-(n_1\cdots n_k)\gt z,\\a_1n_1=a_in_i+h_1-h_i\\ \text{for all}\ i\in\{1,\ldots,k\}}}\chi(n_1)\cdots\chi(n_k).\end{eqnarray}
The reason that makes the sums
![]() $\sum_{n{\leqslant} x}\lambda_z(n+h_1)\ldots\lambda_z(n+h_k)$
easier to deal with lies on the innermost sum of (2·4), where we now have a primitive quadratic character
$\sum_{n{\leqslant} x}\lambda_z(n+h_1)\ldots\lambda_z(n+h_k)$
easier to deal with lies on the innermost sum of (2·4), where we now have a primitive quadratic character
![]() $\chi$
instead of the Liouville function
$\chi$
instead of the Liouville function
![]() $\lambda$
. This character
$\lambda$
. This character
![]() $\chi$
possesses two crucial features that the Liouville function does not. The first one is its periodicity and the second one is the Weil bound that it satisfies (see Lemma 3·5 below).
$\chi$
possesses two crucial features that the Liouville function does not. The first one is its periodicity and the second one is the Weil bound that it satisfies (see Lemma 3·5 below).
Let us now explain how the Weil bound is useful for the estimation of the expression in (2·4). First, we can approximate the indicator function
![]() ${\unicode{x1D7D9}}_{P^-(\cdot)\gt z}$
by
${\unicode{x1D7D9}}_{P^-(\cdot)\gt z}$
by
![]() $1\ast w$
for some suitable sieve weight. This removes the condition
$1\ast w$
for some suitable sieve weight. This removes the condition
![]() $P^-(n_1\cdots n_k)\gt z$
from the innermost sum of (2·4) at the cost of inserting the terms
$P^-(n_1\cdots n_k)\gt z$
from the innermost sum of (2·4) at the cost of inserting the terms
![]() $(1\ast w)(n_1\cdots n_k)$
. After opening these convolutions, we can change the order of summation so that the innermost sums are character sums over polynomial values. So, provided that the contribution of the errors in the approximation
$(1\ast w)(n_1\cdots n_k)$
. After opening these convolutions, we can change the order of summation so that the innermost sums are character sums over polynomial values. So, provided that the contribution of the errors in the approximation
![]() ${\unicode{x1D7D9}}_{P^-(\cdot)\gt z}\approx1\ast w$
can be handled, the estimation of (2·4) ends up being a simple application of the Weil bound to the new innermost character sums. The arguments of this explanation are rigorously executed in Section 5.
${\unicode{x1D7D9}}_{P^-(\cdot)\gt z}\approx1\ast w$
can be handled, the estimation of (2·4) ends up being a simple application of the Weil bound to the new innermost character sums. The arguments of this explanation are rigorously executed in Section 5.
To summarise, the existence of Siegel zeroes is helpful because it puts our focus on the sums
![]() $\sum_{n{\leqslant} x} \lambda_z(n+h_1)\ldots\lambda_z(n+h_k)$
, which one can estimate by combining a sifting argument with the Weil bounds of
$\sum_{n{\leqslant} x} \lambda_z(n+h_1)\ldots\lambda_z(n+h_k)$
, which one can estimate by combining a sifting argument with the Weil bounds of
![]() $\chi$
.
$\chi$
.
3. Auxiliary results
In this section, we state and prove some preparatory results that are needed later for the proof of Theorem 1·2. We start with a lemma which will be used to bound the difference between the sums of the Liouville function
![]() $\lambda$
and those of the functions
$\lambda$
and those of the functions
![]() $\lambda_z$
.
$\lambda_z$
.
Lemma 3·1. Let
![]() $\chi$
be a primitive quadratic character modulo
$\chi$
be a primitive quadratic character modulo
![]() $q{\geqslant} 2$
. Assume that
$q{\geqslant} 2$
. Assume that
![]() $L(\cdot,\chi)$
has a real zero
$L(\cdot,\chi)$
has a real zero
![]() $\beta$
such that
$\beta$
such that
![]() $\beta=1-1/(\eta\log q)$
for some
$\beta=1-1/(\eta\log q)$
for some
![]() $\eta{\geqslant} 10$
. Let
$\eta{\geqslant} 10$
. Let
![]() $z=q^v$
for some
$z=q^v$
for some
![]() $v\gt 0$
. Then for any
$v\gt 0$
. Then for any
![]() $x\gt z$
, we have
$x\gt z$
, we have
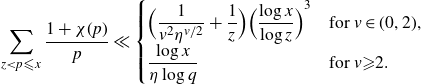 \begin{eqnarray*}\sum_{z \lt p{\leqslant} x}\frac{1+\chi(p)}{p}\ll\begin{cases}\displaystyle{{{\Big( \frac{1}{v^2\eta^{v/2}}+\frac{1}{z}\Big)}}{{\Big(\frac{\log x}{\log z}}\Big)}^3}& \text{for}\ v\in(0,2),\\\displaystyle{\frac{\log x}{\eta\log q}}& \text{for}\ v{\geqslant} 2.\end{cases}\end{eqnarray*}
\begin{eqnarray*}\sum_{z \lt p{\leqslant} x}\frac{1+\chi(p)}{p}\ll\begin{cases}\displaystyle{{{\Big( \frac{1}{v^2\eta^{v/2}}+\frac{1}{z}\Big)}}{{\Big(\frac{\log x}{\log z}}\Big)}^3}& \text{for}\ v\in(0,2),\\\displaystyle{\frac{\log x}{\eta\log q}}& \text{for}\ v{\geqslant} 2.\end{cases}\end{eqnarray*}
Proof. The first branch of the estimate follows from [
Reference Matomäki and Merikoski10
, Lemma 2·2]. Indeed, since
![]() $(1\ast\chi)(n){\geqslant} 0$
for all
$(1\ast\chi)(n){\geqslant} 0$
for all
![]() $n\in{\mathbb{N}}$
, for
$n\in{\mathbb{N}}$
, for
![]() $v\in(0,2)$
, [
Reference Matomäki and Merikoski10
, Lemma 2·2] yields the following (note that in [
Reference Matomäki and Merikoski10
], the authors adopted the notation
$v\in(0,2)$
, [
Reference Matomäki and Merikoski10
, Lemma 2·2] yields the following (note that in [
Reference Matomäki and Merikoski10
], the authors adopted the notation
![]() $\lambda=1\ast\chi$
, whereas they denote the Liouville function by
$\lambda=1\ast\chi$
, whereas they denote the Liouville function by
![]() $\lambda_{\text{Liouville}}$
):
$\lambda_{\text{Liouville}}$
):
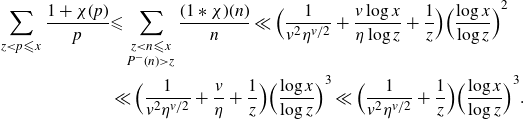 \begin{align*}\sum_{z \lt p{\leqslant} x}\frac{1+\chi(p)}{p}&{\leqslant} \sum_{\substack{z \lt n{\leqslant} x\\P^-(n)\gt z}}\frac{(1\ast\chi)(n)}{n}\ll{\Big(\frac{1}{v^2\eta^{v/2}}+\frac{v\log x}{\eta\log z}+\frac{1}{z}\Big)}{\Big( \frac{\log x}{\log z}\Big)}^2\\&\ll{\Big(\frac{1}{v^2\eta^{v/2}}+\frac{v}{\eta}+\frac{1}{z}\Big)}{\Big( \frac{\log x}{\log z}\Big)}^3\ll {\Big(\frac{1}{v^2\eta^{v/2}}+\frac{1}{z}\Big)}{\Big(\frac{\log x}{\log z}\Big)}^3.\end{align*}
\begin{align*}\sum_{z \lt p{\leqslant} x}\frac{1+\chi(p)}{p}&{\leqslant} \sum_{\substack{z \lt n{\leqslant} x\\P^-(n)\gt z}}\frac{(1\ast\chi)(n)}{n}\ll{\Big(\frac{1}{v^2\eta^{v/2}}+\frac{v\log x}{\eta\log z}+\frac{1}{z}\Big)}{\Big( \frac{\log x}{\log z}\Big)}^2\\&\ll{\Big(\frac{1}{v^2\eta^{v/2}}+\frac{v}{\eta}+\frac{1}{z}\Big)}{\Big( \frac{\log x}{\log z}\Big)}^3\ll {\Big(\frac{1}{v^2\eta^{v/2}}+\frac{1}{z}\Big)}{\Big(\frac{\log x}{\log z}\Big)}^3.\end{align*}
The second branch comes from [ Reference Tao and Teräväinen19 , Proposition 3·5].
The next lemma, which is found as exercise 6(b) in [
Reference Tenenbaum20
, end of Section III·5], allows us to restrict our attention to the summands of
![]() $\sum_{n{\leqslant} x}\lambda_z(n+h_1)\cdots \lambda_z(n+h_k)$
for which the z-smooth parts
$\sum_{n{\leqslant} x}\lambda_z(n+h_1)\cdots \lambda_z(n+h_k)$
for which the z-smooth parts
![]() $\prod_{p{\leqslant} z,\, p^{\alpha}\| n+h_i}p^{\alpha}$
of
$\prod_{p{\leqslant} z,\, p^{\alpha}\| n+h_i}p^{\alpha}$
of
![]() $n+h_i$
are relatively small for all
$n+h_i$
are relatively small for all
![]() $i\in\{1,\ldots,k\}$
.
$i\in\{1,\ldots,k\}$
.
Lemma 3·2. Consider the real numbers
![]() $u{\geqslant} 1$
and
$u{\geqslant} 1$
and
![]() $x, z\gt 1$
. If
$x, z\gt 1$
. If
![]() $x{\geqslant} z^u$
, then
$x{\geqslant} z^u$
, then
Proof. We observe that
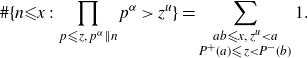 \begin{eqnarray}\#\{n{\leqslant} x\,:\, \prod_{p{\leqslant} z,\, p^{\alpha}\| n}p^{\alpha}\gt z^u\}=\sum_{\substack{ab{\leqslant} x,\,z^u\lt a\\P^+(a){\leqslant} z\lt P^-(b)}}1.\end{eqnarray}
\begin{eqnarray}\#\{n{\leqslant} x\,:\, \prod_{p{\leqslant} z,\, p^{\alpha}\| n}p^{\alpha}\gt z^u\}=\sum_{\substack{ab{\leqslant} x,\,z^u\lt a\\P^+(a){\leqslant} z\lt P^-(b)}}1.\end{eqnarray}
When
![]() $b=1$
, the remaining sum over a is bounded by
$b=1$
, the remaining sum over a is bounded by
![]() $\Psi(x,z)$
. When
$\Psi(x,z)$
. When
![]() $b\gt 1$
, the condition
$b\gt 1$
, the condition
![]() $P^-(b)\gt z$
implies that
$P^-(b)\gt z$
implies that
![]() $b\gt z$
, and so
$b\gt z$
, and so
![]() $a{\leqslant} x/b \lt x/z$
, in this case. For each such a in (3·5), there are at most
$a{\leqslant} x/b \lt x/z$
, in this case. For each such a in (3·5), there are at most
![]() $\Phi(x/a,z)$
integers b. Consequently, the relation (3·5) gives
$\Phi(x/a,z)$
integers b. Consequently, the relation (3·5) gives
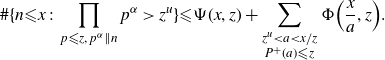 $$ \#\{n{\leqslant} x\,:\, \prod_{p{\leqslant} z,\, p^{\alpha}\| n}p^{\alpha}\gt z^u\}{\leqslant} \Psi(x,z)+\sum_{\substack{z^u \lt a \lt x/z\\P^+(a){\leqslant} z}}\Phi{\Big(\frac{x}{a},z\Big)}.$$
$$ \#\{n{\leqslant} x\,:\, \prod_{p{\leqslant} z,\, p^{\alpha}\| n}p^{\alpha}\gt z^u\}{\leqslant} \Psi(x,z)+\sum_{\substack{z^u \lt a \lt x/z\\P^+(a){\leqslant} z}}\Phi{\Big(\frac{x}{a},z\Big)}.$$
For
![]() $t{\geqslant} z$
, we have the bound
$t{\geqslant} z$
, we have the bound
![]() $\Psi(t,z)\ll xe^{-\log t/(2\log z)}$
[
Reference Tenenbaum20
, Theorem 1 in Section III·5·1]. Since
$\Psi(t,z)\ll xe^{-\log t/(2\log z)}$
[
Reference Tenenbaum20
, Theorem 1 in Section III·5·1]. Since
![]() $x/a\gt z$
, we also have the standard estimate
$x/a\gt z$
, we also have the standard estimate
![]() $\Phi(x/a,z)\ll x/(a\log z)$
, which readily follows e.g. from [
Reference Koukoulopoulos9
, Theorem 14·2] with
$\Phi(x/a,z)\ll x/(a\log z)$
, which readily follows e.g. from [
Reference Koukoulopoulos9
, Theorem 14·2] with
![]() $f={\unicode{x1D7D9}}_{P^-(\cdot)\gt z}$
. Therefore,
$f={\unicode{x1D7D9}}_{P^-(\cdot)\gt z}$
. Therefore,
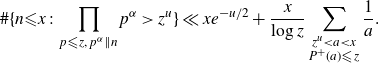 \begin{equation}\#\{n{\leqslant} x\,:\, \prod_{p{\leqslant} z,\, p^{\alpha}\| n}p^{\alpha}\gt z^u\}\ll xe^{-u/2}+\frac{x}{\log z}\sum_{\substack{z^u \lt a \lt x\\P^+(a){\leqslant} z}}\frac{1}{a}.\end{equation}
\begin{equation}\#\{n{\leqslant} x\,:\, \prod_{p{\leqslant} z,\, p^{\alpha}\| n}p^{\alpha}\gt z^u\}\ll xe^{-u/2}+\frac{x}{\log z}\sum_{\substack{z^u \lt a \lt x\\P^+(a){\leqslant} z}}\frac{1}{a}.\end{equation}
Using partial summation and the aforementioned bound on
![]() $\Psi(t,z)$
for
$\Psi(t,z)$
for
![]() $t{\geqslant} z$
, it follows that the sum of the right-hand side of (3·6) is
$t{\geqslant} z$
, it follows that the sum of the right-hand side of (3·6) is
![]() $\ll \log z\cdot e^{-u/2}$
. This concludes the proof of the lemma.
$\ll \log z\cdot e^{-u/2}$
. This concludes the proof of the lemma.
The version of the fundamental lemma of sieve theory that follows provides an approximation of the indicator function
![]() ${\unicode{x1D7D9}}_{P^-(\cdot)\gt z}$
in terms of appropriate sieve weights. It is useful when we deal with sums of the form
${\unicode{x1D7D9}}_{P^-(\cdot)\gt z}$
in terms of appropriate sieve weights. It is useful when we deal with sums of the form
![]() $\sum_{P^-(n)\gt z}\alpha_n$
where
$\sum_{P^-(n)\gt z}\alpha_n$
where
![]() $\alpha_n$
alternate signs.
$\alpha_n$
alternate signs.
Lemma 3·3. There exists a constant
![]() $\beta{\geqslant} 2$
such that the following holds for any
$\beta{\geqslant} 2$
such that the following holds for any
![]() $u{\geqslant} \beta$
.
$u{\geqslant} \beta$
.
Let
![]() $z{\geqslant} 1$
, and define
$z{\geqslant} 1$
, and define
for
![]() $r\in{\mathbb{N}}$
. There exists an arithmetic function
$r\in{\mathbb{N}}$
. There exists an arithmetic function
![]() $w$
such that:
$w$
such that:
-
(i)
 ${\lvert w(n)\rvert}{\leqslant} 1\quad \textit{for all}\quad n\in{\mathbb{N}}$
;
${\lvert w(n)\rvert}{\leqslant} 1\quad \textit{for all}\quad n\in{\mathbb{N}}$
; -
(ii)
 $\mathrm{supp}(w)\subseteq \{d\in{\mathbb{N}}\,:\,d\mid \prod_{p{\leqslant} z}p\textit{ and } d{\leqslant} z^u\};\quad \textit{and}$
$\mathrm{supp}(w)\subseteq \{d\in{\mathbb{N}}\,:\,d\mid \prod_{p{\leqslant} z}p\textit{ and } d{\leqslant} z^u\};\quad \textit{and}$
-
(iii)
 $\displaystyle{{\unicode{x1D7D9}}_{P^-(n)\gt z}=(1\ast w)(n)+O\Big(\tau(n)^2\sum_{r{\geqslant} u-\beta}{\unicode{x1D7D9}}_{P^-(n)\gt z_r}2^{-r}\Big)}\quad \textit{for all}\quad n\in{\mathbb{N}}$
.
$\displaystyle{{\unicode{x1D7D9}}_{P^-(n)\gt z}=(1\ast w)(n)+O\Big(\tau(n)^2\sum_{r{\geqslant} u-\beta}{\unicode{x1D7D9}}_{P^-(n)\gt z_r}2^{-r}\Big)}\quad \textit{for all}\quad n\in{\mathbb{N}}$
.
Proof. See [
Reference Matomäki and Merikoski10
, proof of Lemma 3·2(i)] with
![]() $A=1, \beta=\beta_0$
and a u which here plays the role of the product
$A=1, \beta=\beta_0$
and a u which here plays the role of the product
![]() $u\theta$
for some fixed
$u\theta$
for some fixed
![]() $\theta\in(0,1/3)$
.
$\theta\in(0,1/3)$
.
In the proof of Theorem 1·2, we also make use of the following extention of Shiu’s theorem [ Reference Shiu15 , Theorem 1] which is due to Henriot [Reference Henriot7, Reference Henriot8].
Lemma 3·4. Let k be a positive integer and let
![]() $Q_1,\ldots,Q_k\in{\mathbb{Z}}[X]$
be k pairwise coprime irreducible polynomials. Set
$Q_1,\ldots,Q_k\in{\mathbb{Z}}[X]$
be k pairwise coprime irreducible polynomials. Set
![]() $Q=Q_1\cdots Q_k$
, and denote the degree and determinant of Q by g and D, respectively. For
$Q=Q_1\cdots Q_k$
, and denote the degree and determinant of Q by g and D, respectively. For
![]() $n\in{\mathbb{N}}$
and
$n\in{\mathbb{N}}$
and
![]() $j\in\{1,\ldots,k\}$
, we let
$j\in\{1,\ldots,k\}$
, we let
![]() $\rho_j(n)$
(respectively
$\rho_j(n)$
(respectively
![]() $\rho(n)$
) denote the number of zeroes of
$\rho(n)$
) denote the number of zeroes of
![]() $Q_j$
(respectively Q) modulo n. Assume that Q has no fixed prime divisor, and consider real numbers
$Q_j$
(respectively Q) modulo n. Assume that Q has no fixed prime divisor, and consider real numbers
![]() $A{\geqslant} 1$
,
$A{\geqslant} 1$
,
![]() $B{\geqslant} 1$
,
$B{\geqslant} 1$
,
![]() $\delta\in(0,1)$
, and
$\delta\in(0,1)$
, and
![]() ${\varepsilon}\in(0,1/(100g(g+1/\delta)))$
. Suppose that
${\varepsilon}\in(0,1/(100g(g+1/\delta)))$
. Suppose that
![]() $F:{\mathbb{N}}^k\to{\mathbb{R}}$
is a non-negative function such that
$F:{\mathbb{N}}^k\to{\mathbb{R}}$
is a non-negative function such that
-
(i)
 $F(m_1n_1,\ldots,m_kn_k)=F(m_1,\ldots,m_k)F(n_1,\ldots,n_k)$
$F(m_1n_1,\ldots,m_kn_k)=F(m_1,\ldots,m_k)F(n_1,\ldots,n_k)$
whenever
 $(m_1\cdots m_k,n_1\cdots n_k)=1$
, and
$(m_1\cdots m_k,n_1\cdots n_k)=1$
, and -
(ii)
 $F(n_1,\ldots,n_k){\leqslant} \min\{A^{\Omega(n_1\cdots n_k)},B(n_1\cdots n_k)^{{\varepsilon}}\}\quad \text{for all}\quad (n_1,\ldots,n_k)\in{\mathbb{N}}^k.$
$F(n_1,\ldots,n_k){\leqslant} \min\{A^{\Omega(n_1\cdots n_k)},B(n_1\cdots n_k)^{{\varepsilon}}\}\quad \text{for all}\quad (n_1,\ldots,n_k)\in{\mathbb{N}}^k.$
There exists a constant
![]() $c_0\gt 0$
, depending at most on
$c_0\gt 0$
, depending at most on
![]() $g, A, B$
and
$g, A, B$
and
![]() $\delta$
, su
ch that
$\delta$
, su
ch that
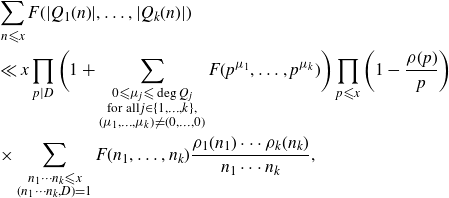 \begin{align*}&\sum_{n{\leqslant} x}F(\lvert{Q_1(n)}\rvert,\ldots,\lvert{Q_k(n)}\rvert)\\&\ll x\prod_{p\mid D}\bigg(1+\sum_{\substack{0{\leqslant} \mu_j{\leqslant} \deg Q_j\\ \text{for all}\,j\in\{1,\ldots,k\},\\(\mu_1,\ldots,\mu_k)\neq (0,\ldots,0)}}F(p^{\mu_1},\ldots,p^{\mu_k})\bigg)\prod_{p{\leqslant} x}\bigg(1-\frac{\rho(p)}{p}\bigg)\\&\times\sum_{\substack{n_1\cdots n_k{\leqslant} x\\(n_1\cdots n_k,D)=1}}F(n_1,\ldots,n_k)\frac{\rho_1(n_1)\cdots \rho_k(n_k)}{n_1\cdots n_k},\end{align*}
\begin{align*}&\sum_{n{\leqslant} x}F(\lvert{Q_1(n)}\rvert,\ldots,\lvert{Q_k(n)}\rvert)\\&\ll x\prod_{p\mid D}\bigg(1+\sum_{\substack{0{\leqslant} \mu_j{\leqslant} \deg Q_j\\ \text{for all}\,j\in\{1,\ldots,k\},\\(\mu_1,\ldots,\mu_k)\neq (0,\ldots,0)}}F(p^{\mu_1},\ldots,p^{\mu_k})\bigg)\prod_{p{\leqslant} x}\bigg(1-\frac{\rho(p)}{p}\bigg)\\&\times\sum_{\substack{n_1\cdots n_k{\leqslant} x\\(n_1\cdots n_k,D)=1}}F(n_1,\ldots,n_k)\frac{\rho_1(n_1)\cdots \rho_k(n_k)}{n_1\cdots n_k},\end{align*}
for all
![]() $x{\geqslant} c_0\Vert Q \Vert^{\delta}$
, where
$x{\geqslant} c_0\Vert Q \Vert^{\delta}$
, where
![]() $\Vert Q \Vert$
denotes the sum of the absolute values of the coefficients of Q. The implicit constant in the bound depends at most on
$\Vert Q \Vert$
denotes the sum of the absolute values of the coefficients of Q. The implicit constant in the bound depends at most on
![]() $g, A, B$
and
$g, A, B$
and
![]() $\delta$
.
$\delta$
.
Proof. It follows from [
Reference Henriot7
, Theorem 3] upon noticing that we can trivially bound the Euler product
![]() $\Delta_D$
in its statement by the simpler product
$\Delta_D$
in its statement by the simpler product
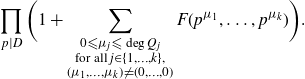 $$ \prod_{p\mid D}\bigg(1+\sum_{\substack{0{\leqslant} \mu_j{\leqslant} \deg Q_j\\ \text{for all}\,j\in\{1,\ldots,k\},\\(\mu_1,\ldots,\mu_k)\neq (0,\ldots,0)}}F(p^{\mu_1},\ldots,p^{\mu_k})\bigg).$$
$$ \prod_{p\mid D}\bigg(1+\sum_{\substack{0{\leqslant} \mu_j{\leqslant} \deg Q_j\\ \text{for all}\,j\in\{1,\ldots,k\},\\(\mu_1,\ldots,\mu_k)\neq (0,\ldots,0)}}F(p^{\mu_1},\ldots,p^{\mu_k})\bigg).$$
We will not need Lemma 3·4 in its full generality. In fact, we can only think of F as a product of divisor functions with a coprimality condition, whereas
![]() $Q_1,\ldots,Q_k$
are simply going to be linear polynomials.
$Q_1,\ldots,Q_k$
are simply going to be linear polynomials.
Another useful result for the proof of Theorem 1·2 is the following generalisation of the classical Weil bound for character sums [ Reference Schmidt14 , Theorem 2C′].
Lemma 3·5. Let
![]() $\chi$
be a primitive quadratic character modulo
$\chi$
be a primitive quadratic character modulo
![]() $q{\geqslant} 2$
, and consider a polynomial
$q{\geqslant} 2$
, and consider a polynomial
![]() $f\in{\mathbb{Z}}[X]$
. Let also M and
$f\in{\mathbb{Z}}[X]$
. Let also M and
![]() $N{\geqslant} 0$
be two integers. If
$N{\geqslant} 0$
be two integers. If
![]() $q^*$
is the product of the odd prime factors p of q for which f is a constant multiple of a square polynomial modulo p, then
$q^*$
is the product of the odd prime factors p of q for which f is a constant multiple of a square polynomial modulo p, then
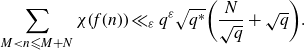 $$ \sum_{M \lt n{\leqslant} M+N}\chi(f(n))\ll_{{\varepsilon}}q^{{\varepsilon}}\sqrt{q^*}\bigg(\frac{N}{\sqrt{q}}+\sqrt{q}\bigg).$$
$$ \sum_{M \lt n{\leqslant} M+N}\chi(f(n))\ll_{{\varepsilon}}q^{{\varepsilon}}\sqrt{q^*}\bigg(\frac{N}{\sqrt{q}}+\sqrt{q}\bigg).$$
Proof. See the discussion preceding the statement of Lemma 3·7 in [ Reference Tao and Teräväinen19 , Subsection 3·4]
We close the section with an inequality which was stated without proof in [ Reference Chinis1 , Subsection 4·2].
Lemma 3·6. Let k be a positive integer. For given
![]() $m_1,\ldots,m_k\in{\mathbb{N}}$
, we have
$m_1,\ldots,m_k\in{\mathbb{N}}$
, we have
Proof. For
![]() $k=1$
the lemma is trivial and we may assume that
$k=1$
the lemma is trivial and we may assume that
![]() $k{\geqslant} 2$
. We start by making use of the following elementary observation; For positive integers a,b and c for which
$k{\geqslant} 2$
. We start by making use of the following elementary observation; For positive integers a,b and c for which
![]() $b\mid c$
, it is true that
$b\mid c$
, it is true that
![]() $(a,b){\leqslant} (a,c)$
. We apply this property and obtain
$(a,b){\leqslant} (a,c)$
. We apply this property and obtain
It is also easy to note that
![]() $(ab,c){\leqslant} (a,c)(b,c)$
for
$(ab,c){\leqslant} (a,c)(b,c)$
for
![]() $a,b,c\in{\mathbb{N}}$
. Hence,
$a,b,c\in{\mathbb{N}}$
. Hence,
Now, we put (3·7) and (3·8) together and deduce that
Based on this inequality, the proof is completed by induction on k.
4. Preparations for the Proof of Theorem 1·2
Throughout this and the following section, we assume that
![]() ${\varepsilon}, k$
and
${\varepsilon}, k$
and
![]() $h_1, \ldots, h_k$
are fixed. Hence, any dependence of the implicit constants on any of these integers is ignored. Moreover, recall that for
$h_1, \ldots, h_k$
are fixed. Hence, any dependence of the implicit constants on any of these integers is ignored. Moreover, recall that for
![]() $z\gt 1$
, the completely multiplicative function
$z\gt 1$
, the completely multiplicative function
![]() $\lambda_{z}$
is defined by (2·2), where the Dirichlet character
$\lambda_{z}$
is defined by (2·2), where the Dirichlet character
![]() $\chi$
in (2·2) is now the primitive quadratic character modulo q from the statement of Theorem 1·2.
$\chi$
in (2·2) is now the primitive quadratic character modulo q from the statement of Theorem 1·2.
4·1. Going from
 $\lambda$
to
$\lambda$
to
 $\lambda_z$
$\lambda_z$
As was explained in Section 2, our first objective is to make a transition from the sums
![]() $\sum_{n {\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k)$
to the sums
$\sum_{n {\leqslant} x} \lambda(n+h_1)\cdots\lambda(n+h_k)$
to the sums
![]() $\sum_{n {\leqslant} x} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)$
. To this end, we prove the following.
$\sum_{n {\leqslant} x} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)$
. To this end, we prove the following.
Lemma 4·1 Let
![]() $k,q{\geqslant} 2$
be natural numbers, and let
$k,q{\geqslant} 2$
be natural numbers, and let
![]() $h_1,\ldots,h_k$
be distinct non-negative integers. Let also
$h_1,\ldots,h_k$
be distinct non-negative integers. Let also
![]() $\chi$
be as in the statement of Theorem 1·2 and write
$\chi$
be as in the statement of Theorem 1·2 and write
![]() $z=q^v$
for some
$z=q^v$
for some
![]() $v\gt 0$
. For
$v\gt 0$
. For
![]() $x\gt z$
, we have that
$x\gt z$
, we have that
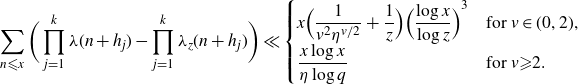 \begin{eqnarray*}\sum_{n {\leqslant} x}\bigg(\prod_{j=1}^k\lambda(n+h_j)-\prod_{j=1}^k\lambda_{z}(n+h_j)\bigg)\ll\begin{cases}\displaystyle{x{\Big(\frac{1}{v^2\eta^{v/2}}+\frac{1}{z}\Big)}{\Big(\frac{\log x}{\log z}\Big)}^3}& \text{for}\ v\in(0,2),\\\displaystyle{\frac{x\log x}{\eta\log q}}&\text{for}\ v{\geqslant} 2.\end{cases}\end{eqnarray*}
\begin{eqnarray*}\sum_{n {\leqslant} x}\bigg(\prod_{j=1}^k\lambda(n+h_j)-\prod_{j=1}^k\lambda_{z}(n+h_j)\bigg)\ll\begin{cases}\displaystyle{x{\Big(\frac{1}{v^2\eta^{v/2}}+\frac{1}{z}\Big)}{\Big(\frac{\log x}{\log z}\Big)}^3}& \text{for}\ v\in(0,2),\\\displaystyle{\frac{x\log x}{\eta\log q}}&\text{for}\ v{\geqslant} 2.\end{cases}\end{eqnarray*}
Proof. The beginning of the proof is similar to those of [ Reference Chinis1 , Lemma 3·1] and [ Reference Germán and Kátai3 , Section 3, relation (3·3)], but for the sake of completeness we write it down here.
We will need the following inequality that one can prove by induction; If
![]() $m\in{\mathbb{N}}$
and
$m\in{\mathbb{N}}$
and
![]() $w_1,\ldots,w_m,$
$w_1,\ldots,w_m,$
![]() $u_1,\ldots,u_m$
are complex numbers of modulus at most 1, then
$u_1,\ldots,u_m$
are complex numbers of modulus at most 1, then
Using this inequality, we infer that
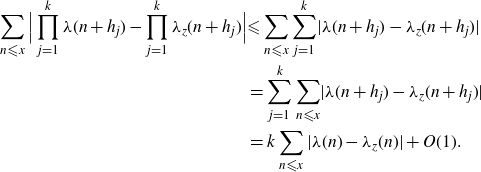 \begin{align}\begin{split}\sum_{n {\leqslant} x}{\Big\lvert\prod_{j=1}^k\lambda(n+h_j) - \prod_{j=1}^k\lambda_{z}(n+h_j)\Big\rvert}&{\leqslant} \sum_{n{\leqslant} x}\sum_{j=1}^k\lvert{\lambda(n+h_j)-\lambda_z(n+h_j)}\rvert\\&=\sum_{j=1}^k\sum_{n{\leqslant} x}\lvert{\lambda(n+h_j)-\lambda_z(n+h_j)}\rvert\\&=k\sum_{n {\leqslant} x} |\lambda(n)-\lambda_{z}(n)| + O(1).\end{split}\end{align}
\begin{align}\begin{split}\sum_{n {\leqslant} x}{\Big\lvert\prod_{j=1}^k\lambda(n+h_j) - \prod_{j=1}^k\lambda_{z}(n+h_j)\Big\rvert}&{\leqslant} \sum_{n{\leqslant} x}\sum_{j=1}^k\lvert{\lambda(n+h_j)-\lambda_z(n+h_j)}\rvert\\&=\sum_{j=1}^k\sum_{n{\leqslant} x}\lvert{\lambda(n+h_j)-\lambda_z(n+h_j)}\rvert\\&=k\sum_{n {\leqslant} x} |\lambda(n)-\lambda_{z}(n)| + O(1).\end{split}\end{align}
In order to bound
![]() $\sum_{n {\leqslant} x} |\lambda(n)-\lambda_{z}(n)|$
, we are exploiting the inequality (4·9) again. We combine it with the definition of
$\sum_{n {\leqslant} x} |\lambda(n)-\lambda_{z}(n)|$
, we are exploiting the inequality (4·9) again. We combine it with the definition of
![]() $\lambda_z$
and get
$\lambda_z$
and get
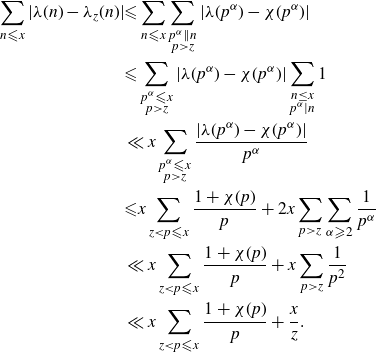 \begin{align}\begin{aligned}\sum_{n {\leqslant} x} |\lambda(n)-\lambda_{z}(n)| &{\leqslant} \sum_{n {\leqslant} x}\sum_{\substack{p^{\alpha}\|n \\ p\gt z}} |\lambda(p^{\alpha})-\chi(p^{\alpha})|\\&{\leqslant} \sum_{\substack{p^{\alpha}{\leqslant} x \\ p\gt z}} |\lambda(p^{\alpha})-\chi(p^{\alpha})|\sum_{\substack{n \le x \\ p^{\alpha}|n}} 1 \\&\ll x\sum_{\substack{p^{\alpha}{\leqslant} x \\ p\gt z}} \frac{|\lambda(p^{\alpha})-\chi(p^{\alpha})|}{p^{\alpha}}\\&{\leqslant} x\sum_{z\lt p{\leqslant} x}\frac{1+\chi(p)}{p}+2x\sum_{p\gt z}\sum_{\alpha {\geqslant} 2}\frac{1}{p^{\alpha}} \\&\ll x\sum_{z \lt p {\leqslant} x}\frac{1+\chi(p)}{p}+x\sum_{p\gt z}\frac{1}{p^2}\\&\ll x\sum_{z \lt p {\leqslant} x}\frac{1+\chi(p)}{p}+\frac{x}{z}.\end{aligned}\end{align}
\begin{align}\begin{aligned}\sum_{n {\leqslant} x} |\lambda(n)-\lambda_{z}(n)| &{\leqslant} \sum_{n {\leqslant} x}\sum_{\substack{p^{\alpha}\|n \\ p\gt z}} |\lambda(p^{\alpha})-\chi(p^{\alpha})|\\&{\leqslant} \sum_{\substack{p^{\alpha}{\leqslant} x \\ p\gt z}} |\lambda(p^{\alpha})-\chi(p^{\alpha})|\sum_{\substack{n \le x \\ p^{\alpha}|n}} 1 \\&\ll x\sum_{\substack{p^{\alpha}{\leqslant} x \\ p\gt z}} \frac{|\lambda(p^{\alpha})-\chi(p^{\alpha})|}{p^{\alpha}}\\&{\leqslant} x\sum_{z\lt p{\leqslant} x}\frac{1+\chi(p)}{p}+2x\sum_{p\gt z}\sum_{\alpha {\geqslant} 2}\frac{1}{p^{\alpha}} \\&\ll x\sum_{z \lt p {\leqslant} x}\frac{1+\chi(p)}{p}+x\sum_{p\gt z}\frac{1}{p^2}\\&\ll x\sum_{z \lt p {\leqslant} x}\frac{1+\chi(p)}{p}+\frac{x}{z}.\end{aligned}\end{align}
From (4·10) and (4·11), we deduce that
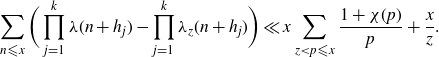 \begin{equation*}\sum_{n {\leqslant} x}\bigg(\prod_{j=1}^k\lambda(n+h_j)-\prod_{j=1}^k\lambda_{z}(n+h_j)\bigg)\ll x\sum_{z \lt p {\leqslant} x}\frac{1+\chi(p)}{p}+\frac{x}{z}.\end{equation*}
\begin{equation*}\sum_{n {\leqslant} x}\bigg(\prod_{j=1}^k\lambda(n+h_j)-\prod_{j=1}^k\lambda_{z}(n+h_j)\bigg)\ll x\sum_{z \lt p {\leqslant} x}\frac{1+\chi(p)}{p}+\frac{x}{z}.\end{equation*}
The proof is now completed by an application of Lemma 3·1. In the case
![]() $v\lt 2$
, Lemma 3·1 completes the proof immediately because
$v\lt 2$
, Lemma 3·1 completes the proof immediately because
![]() $x/z$
is smaller than
$x/z$
is smaller than
![]() $x(\log x)^3/(z(\log z)^3)$
for
$x(\log x)^3/(z(\log z)^3)$
for
![]() $x\gt z$
. When
$x\gt z$
. When
![]() $v{\geqslant} 2$
, the extra term
$v{\geqslant} 2$
, the extra term
![]() $x/z$
is absorbed by the bound
$x/z$
is absorbed by the bound
![]() $x\log x/(\eta\log q)$
, because in this case
$x\log x/(\eta\log q)$
, because in this case
![]() $\log x{\geqslant} \log q$
and (1·1) implies that
$\log x{\geqslant} \log q$
and (1·1) implies that
![]() $\eta\ll q{\leqslant} z$
.
$\eta\ll q{\leqslant} z$
.
4·2. Restricting the z-smooth parts
Once Lemma 4·1 is used and the transition from the sums of
![]() $\lambda$
to the sums of
$\lambda$
to the sums of
![]() $\lambda_z$
is completed, one’s interest turns to the study of
$\lambda_z$
is completed, one’s interest turns to the study of
![]() $\sum_{n {\leqslant} x} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)$
. For technical reasons, we seek to exclude the terms of
$\sum_{n {\leqslant} x} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)$
. For technical reasons, we seek to exclude the terms of
![]() $\sum_{n {\leqslant} x} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)$
for which
$\sum_{n {\leqslant} x} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)$
for which
![]() $\prod_{p{\leqslant} z,\, p^{\alpha}\| n+h_i}p^{\alpha}$
is relatively large for some
$\prod_{p{\leqslant} z,\, p^{\alpha}\| n+h_i}p^{\alpha}$
is relatively large for some
![]() $i\in\{1,\ldots,k\}$
. To this end, in the current subsection, we assess the contribution stemming from these “undesirable” summands.
$i\in\{1,\ldots,k\}$
. To this end, in the current subsection, we assess the contribution stemming from these “undesirable” summands.
Before doing so, we introduce the following notation for convenience; For
![]() $m\in{\mathbb{N}}$
and
$m\in{\mathbb{N}}$
and
![]() $z\gt 1$
, we write
$z\gt 1$
, we write
Lemma 4·2. Let
![]() $x{\geqslant} z\gt 1$
and
$x{\geqslant} z\gt 1$
and
![]() $u{\geqslant} 1$
. If
$u{\geqslant} 1$
. If
![]() $x{\geqslant} z^u$
, then
$x{\geqslant} z^u$
, then
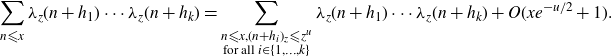 \begin{align*}\sum_{n {\leqslant} x}\lambda_{z}(n+h_1)\cdots\lambda_z(n+h_k)=\sum_{\substack{n {\leqslant} x, (n+h_i)_{z} {\leqslant} z^{u}\\ \text{for all } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)+O(xe^{-u/2}+1).\end{align*}
\begin{align*}\sum_{n {\leqslant} x}\lambda_{z}(n+h_1)\cdots\lambda_z(n+h_k)=\sum_{\substack{n {\leqslant} x, (n+h_i)_{z} {\leqslant} z^{u}\\ \text{for all } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)+O(xe^{-u/2}+1).\end{align*}
Proof. We readily see that
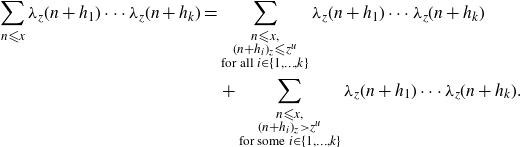 \begin{align}\sum_{n {\leqslant} x}\lambda_{z}(n+h_1)\cdots\lambda_z(n+h_k)&=\sum_{\substack{n {\leqslant} x, \nonumber\\ (n+h_i)_{z} {\leqslant} z^{u}\\ \text{for all } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)\\&\quad+\sum_{\substack{n {\leqslant} x, \\ (n+h_i)_{z} \gt z^{u} \\ \text{for some } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k).\end{align}
\begin{align}\sum_{n {\leqslant} x}\lambda_{z}(n+h_1)\cdots\lambda_z(n+h_k)&=\sum_{\substack{n {\leqslant} x, \nonumber\\ (n+h_i)_{z} {\leqslant} z^{u}\\ \text{for all } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)\\&\quad+\sum_{\substack{n {\leqslant} x, \\ (n+h_i)_{z} \gt z^{u} \\ \text{for some } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k).\end{align}
Note that
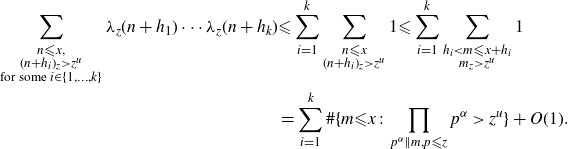 \begin{align*}\sum_{\substack{n {\leqslant} x, \\ (n+h_i)_{z} \gt z^{u} \\ \text{for some } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k) &{\leqslant} \sum_{i=1}^{k} \sum_{\substack{n {\leqslant} x \\ (n+h_i)_{z} \gt z^{u}}} 1 {\leqslant} \sum_{i=1}^{k} \sum_{\substack{h_i \lt m {\leqslant} x+h_i \\ m_{z} \gt z^{u}}} 1\\&= \sum_{i=1}^{k} \#\{ m {\leqslant} x\,:\, \prod_{p^{\alpha}\| m, p{\leqslant} z} p^{\alpha} \gt z^u \} + O(1).\end{align*}
\begin{align*}\sum_{\substack{n {\leqslant} x, \\ (n+h_i)_{z} \gt z^{u} \\ \text{for some } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k) &{\leqslant} \sum_{i=1}^{k} \sum_{\substack{n {\leqslant} x \\ (n+h_i)_{z} \gt z^{u}}} 1 {\leqslant} \sum_{i=1}^{k} \sum_{\substack{h_i \lt m {\leqslant} x+h_i \\ m_{z} \gt z^{u}}} 1\\&= \sum_{i=1}^{k} \#\{ m {\leqslant} x\,:\, \prod_{p^{\alpha}\| m, p{\leqslant} z} p^{\alpha} \gt z^u \} + O(1).\end{align*}
Therefore, by using Lemma 3·2, we deduce that
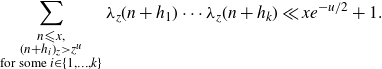 \begin{equation}\sum_{\substack{n {\leqslant} x, \\ (n+h_i)_{z} \gt z^{u} \\ \text{for some } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k) \ll xe^{-u/2} + 1.\end{equation}
\begin{equation}\sum_{\substack{n {\leqslant} x, \\ (n+h_i)_{z} \gt z^{u} \\ \text{for some } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k) \ll xe^{-u/2} + 1.\end{equation}
4·3. Rewriting the “main term” in Lemma 4·2
Let x, z and u be as in the statement of Lemma 4·2. We are going to rewrite the sum
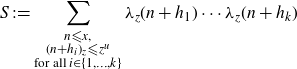 \begin{equation}S\,:\!=\sum_{\substack{n {\leqslant} x, \\ (n+h_i)_{z} {\leqslant} z^{u}\\ \text{for all } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)\end{equation}
\begin{equation}S\,:\!=\sum_{\substack{n {\leqslant} x, \\ (n+h_i)_{z} {\leqslant} z^{u}\\ \text{for all } i \in \{1,\ldots,k\}}} \lambda_{z}(n+h_1)\cdots\lambda_{z}(n+h_k)\end{equation}
in a form that we use in the upcoming section. For the sequel, we assume without loss of generality that
![]() $h_1 = \min_{1 {\leqslant} i {\leqslant} k} h_i$
. We write
$h_1 = \min_{1 {\leqslant} i {\leqslant} k} h_i$
. We write
![]() $n+h_i=a_in_i$
with
$n+h_i=a_in_i$
with
![]() $P^+(a_i){\leqslant} z$
and
$P^+(a_i){\leqslant} z$
and
![]() $P^-(n_i)\gt z$
, and so
$P^-(n_i)\gt z$
, and so
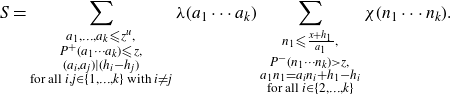 \begin{align}S = \sum_{\substack{a_1, \ldots, a_k {\leqslant} z^{u}, \\ P^{+}(a_1\cdots a_k) {\leqslant} z, \\ (a_i,a_j) |(h_i-h_j) \\ \text{for all } i,j \in \{1,\ldots,k\} \textrm{ with } i\not=j}}\lambda(a_1\cdots a_k)\sum_{\substack{n_1 {\leqslant} \frac{x+h_1}{a_1}, \\ P^{-}(n_1\cdots n_k) \gt z, \\ a_{1}n_{1} = a_{i}n_{i}+h_1-h_i \\ \text{for all } i \in \{2,\ldots,k\}}} \chi(n_1\cdots n_k).\end{align}
\begin{align}S = \sum_{\substack{a_1, \ldots, a_k {\leqslant} z^{u}, \\ P^{+}(a_1\cdots a_k) {\leqslant} z, \\ (a_i,a_j) |(h_i-h_j) \\ \text{for all } i,j \in \{1,\ldots,k\} \textrm{ with } i\not=j}}\lambda(a_1\cdots a_k)\sum_{\substack{n_1 {\leqslant} \frac{x+h_1}{a_1}, \\ P^{-}(n_1\cdots n_k) \gt z, \\ a_{1}n_{1} = a_{i}n_{i}+h_1-h_i \\ \text{for all } i \in \{2,\ldots,k\}}} \chi(n_1\cdots n_k).\end{align}
We denote the inner sum in (4·15) by
![]() $\Sigma$
, that is,
$\Sigma$
, that is,
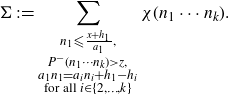 \begin{align*}\Sigma \,:\!= \sum_{\substack{n_1 {\leqslant} \frac{x+h_1}{a_1}, \\ P^{-}(n_1\cdots n_k) \gt z, \\ a_{1}n_{1} = a_{i}n_{i}+h_1-h_i \\ \text{for all } i \in \{2,\ldots,k\}}} \chi(n_1\cdots n_k).\end{align*}
\begin{align*}\Sigma \,:\!= \sum_{\substack{n_1 {\leqslant} \frac{x+h_1}{a_1}, \\ P^{-}(n_1\cdots n_k) \gt z, \\ a_{1}n_{1} = a_{i}n_{i}+h_1-h_i \\ \text{for all } i \in \{2,\ldots,k\}}} \chi(n_1\cdots n_k).\end{align*}
Upon writing
![]() $h_i^* = h_i - h_1$
for
$h_i^* = h_i - h_1$
for
![]() $i \in \{1,\ldots,k\}$
, we see that
$i \in \{1,\ldots,k\}$
, we see that
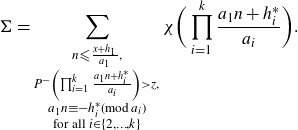 \begin{align}\Sigma = \sum_{\substack{n {\leqslant} \frac{x+h_1}{a_1}, \\ P^{-}\left( \prod_{i=1}^{k}\frac{a_{1}n+h_{i}^*}{a_i} \right)\gt z, \\ a_{1}n\equiv -h_i^* (\mathrm{mod}\,{a_i}) \\ \text{for all } i \in \{2,\ldots,k\}}} \chi\bigg( \prod_{i=1}^{k}\frac{a_{1}n+h_{i}^*}{a_i} \bigg).\end{align}
\begin{align}\Sigma = \sum_{\substack{n {\leqslant} \frac{x+h_1}{a_1}, \\ P^{-}\left( \prod_{i=1}^{k}\frac{a_{1}n+h_{i}^*}{a_i} \right)\gt z, \\ a_{1}n\equiv -h_i^* (\mathrm{mod}\,{a_i}) \\ \text{for all } i \in \{2,\ldots,k\}}} \chi\bigg( \prod_{i=1}^{k}\frac{a_{1}n+h_{i}^*}{a_i} \bigg).\end{align}
Since we have the condition
![]() $(a_i,a_j)|(h_i-h_j)$
in the outermost sum of (4·15), for every
$(a_i,a_j)|(h_i-h_j)$
in the outermost sum of (4·15), for every
![]() $i \in \{1,\ldots,k\}$
, one has that
$i \in \{1,\ldots,k\}$
, one has that
 \begin{align}\begin{split}a_{1}n \equiv -h_i^* \;(\mathrm{mod}\,{a_i}) &\Longleftrightarrow \frac{a_1}{(a_1,a_i)}n \equiv -\frac{h_i^*}{(a_1,a_i)}\; \left(\mathrm{mod}\,\frac{a_i}{(a_1,a_i)}\right) \\&\Longleftrightarrow n \equiv -\overline{a_{1,i}}\frac{h_i^*}{(a_1,a_i)}\;(\mathrm{mod}\, a_i^*),\end{split}\end{align}
\begin{align}\begin{split}a_{1}n \equiv -h_i^* \;(\mathrm{mod}\,{a_i}) &\Longleftrightarrow \frac{a_1}{(a_1,a_i)}n \equiv -\frac{h_i^*}{(a_1,a_i)}\; \left(\mathrm{mod}\,\frac{a_i}{(a_1,a_i)}\right) \\&\Longleftrightarrow n \equiv -\overline{a_{1,i}}\frac{h_i^*}{(a_1,a_i)}\;(\mathrm{mod}\, a_i^*),\end{split}\end{align}
where
![]() $a_i^* \,:\!= a_{i}(a_1,a_i)^{-1}$
,
$a_i^* \,:\!= a_{i}(a_1,a_i)^{-1}$
,
![]() $a_{1,i}\,:\!=a_{1}(a_1,a_i)^{-1},$
and
$a_{1,i}\,:\!=a_{1}(a_1,a_i)^{-1},$
and
![]() $\overline{a_{1,i}}$
is its inverse
$\overline{a_{1,i}}$
is its inverse
![]() $(\mathrm{mod}\, a_i^*)$
. Now, if the system of linear congruences (4·17) is not soluble, then
$(\mathrm{mod}\, a_i^*)$
. Now, if the system of linear congruences (4·17) is not soluble, then
![]() $\Sigma=0$
and there is no contribution from such systems. Consequently, we may limit the outermost sum of (4·15) to those
$\Sigma=0$
and there is no contribution from such systems. Consequently, we may limit the outermost sum of (4·15) to those
![]() $a_1,\ldots,a_k$
for which the system of linear congruences (4·17) is soluble. In this case, by the Chinese Remainder Theorem, there exists an integer
$a_1,\ldots,a_k$
for which the system of linear congruences (4·17) is soluble. In this case, by the Chinese Remainder Theorem, there exists an integer
![]() $r^*$
such that:
$r^*$
such that:
-
(i)
 $0 \lt r^* {\leqslant} [a_{2}^*, \ldots, a_{k}^*]$
;
$0 \lt r^* {\leqslant} [a_{2}^*, \ldots, a_{k}^*]$
; -
(ii)
 $n = \ell[a_{2}^*, \ldots, a_{k}^*]+r^*-[a_{2}^*, \ldots, a_{k}^*]$
for
$n = \ell[a_{2}^*, \ldots, a_{k}^*]+r^*-[a_{2}^*, \ldots, a_{k}^*]$
for
 $\ell \in {\mathbb{N}};$
and
$\ell \in {\mathbb{N}};$
and -
(iii)
 $a_{1}r^* \equiv -h_i^* \; (\mathrm{mod}\,{a_i})$
for all
$a_{1}r^* \equiv -h_i^* \; (\mathrm{mod}\,{a_i})$
for all
 $i \in \{1,\ldots,k\}$
.
$i \in \{1,\ldots,k\}$
.
Applying these to (4·16), we derive that
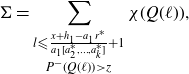 \begin{align}\Sigma = \sum_{\substack{l {\leqslant} \frac{x+h_1-a_{1}r^*}{a_{1}[a_{2}^*, \ldots, a_{k}^*]}+1 \\ P^{-}(Q(\ell))\gt z}}\chi(Q(\ell)),\end{align}
\begin{align}\Sigma = \sum_{\substack{l {\leqslant} \frac{x+h_1-a_{1}r^*}{a_{1}[a_{2}^*, \ldots, a_{k}^*]}+1 \\ P^{-}(Q(\ell))\gt z}}\chi(Q(\ell)),\end{align}
where
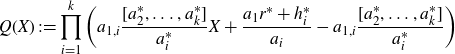 \begin{align*}Q(X) \,:\!= \prod_{i=1}^{k}\left( a_{1,i}\frac{[a_{2}^*, \ldots, a_{k}^*]}{a_i^*}X+\frac{a_{1}r^*+h_{i}^*}{a_i}-a_{1,i}\frac{[a_{2}^*, \ldots, a_{k}^*]}{a_{i}^*} \right)\end{align*}
\begin{align*}Q(X) \,:\!= \prod_{i=1}^{k}\left( a_{1,i}\frac{[a_{2}^*, \ldots, a_{k}^*]}{a_i^*}X+\frac{a_{1}r^*+h_{i}^*}{a_i}-a_{1,i}\frac{[a_{2}^*, \ldots, a_{k}^*]}{a_{i}^*} \right)\end{align*}
defines a polynomial of
![]() ${\mathbb{Z}}[X]$
. Since
${\mathbb{Z}}[X]$
. Since
![]() $\Sigma$
denotes the inner sum of (4·15), by inserting (4·18) into (4·15), we obtain that
$\Sigma$
denotes the inner sum of (4·15), by inserting (4·18) into (4·15), we obtain that
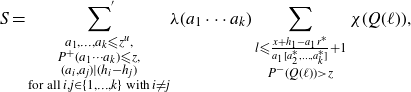 \begin{align}S = {\sideset{}{^{'}}\sum_{\substack{a_1, \ldots, a_k {\leqslant} z^{u}, \\ P^{+}(a_1\cdots a_k) {\leqslant} z, \\ (a_i,a_j) |(h_i-h_j) \\ \text{for all } i,j \in \{1,\ldots,k\} \text{ with } i\not=j}}}\lambda(a_1\cdots a_k)\sum_{\substack{l {\leqslant} \frac{x+h_1-a_{1}r^*}{a_{1}[a_{2}^*, \ldots, a_{k}^*]}+1 \\ P^{-}(Q(\ell))\gt z}}\chi(Q(\ell)),\end{align}
\begin{align}S = {\sideset{}{^{'}}\sum_{\substack{a_1, \ldots, a_k {\leqslant} z^{u}, \\ P^{+}(a_1\cdots a_k) {\leqslant} z, \\ (a_i,a_j) |(h_i-h_j) \\ \text{for all } i,j \in \{1,\ldots,k\} \text{ with } i\not=j}}}\lambda(a_1\cdots a_k)\sum_{\substack{l {\leqslant} \frac{x+h_1-a_{1}r^*}{a_{1}[a_{2}^*, \ldots, a_{k}^*]}+1 \\ P^{-}(Q(\ell))\gt z}}\chi(Q(\ell)),\end{align}
where the prime
![]() $^{'}$
indicates that the sum is taken over the integers
$^{'}$
indicates that the sum is taken over the integers
![]() $a_1,\ldots,a_k$
for which the system of congruences (4·17) is soluble.
$a_1,\ldots,a_k$
for which the system of congruences (4·17) is soluble.
Relation (4·19) provides the form of S that we will exploit.
5. Proof of Theorem 1·2
In this section, we establish Theorem 1·2. To achieve this, we bound S by starting from (4·19), and then, once the estimation of S is complete, we combine the definition (4·14) of S with Lemmas 4·1 and 4·2.
Let
![]() $z=q^v$
with
$z=q^v$
with
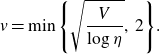 $$ v=\min\Bigg\{\sqrt{\frac{V}{\log\eta}},\,2\Bigg\}.$$
$$ v=\min\Bigg\{\sqrt{\frac{V}{\log\eta}},\,2\Bigg\}.$$
We now assume that
![]() $\eta$
is sufficiently large, otherwise
$\eta$
is sufficiently large, otherwise
![]() $xV/\eta\gg x$
, in which case, Theorem 1·2 would immediately follow from the trivial bound x. Since
$xV/\eta\gg x$
, in which case, Theorem 1·2 would immediately follow from the trivial bound x. Since
![]() $\eta$
is assumed to be large enough, Siegel’s theorem, that is (1·1), implies that q is also sufficiently large and that
$\eta$
is assumed to be large enough, Siegel’s theorem, that is (1·1), implies that q is also sufficiently large and that
![]() $v\gg1/\sqrt{(\log q)}$
. Therefore,
$v\gg1/\sqrt{(\log q)}$
. Therefore,
![]() $v {\geqslant} \log{k}/\log{q}$
, and so
$v {\geqslant} \log{k}/\log{q}$
, and so
![]() $z = q^v {\geqslant} k$
.
$z = q^v {\geqslant} k$
.
In (4·19), we have that
![]() $P^+(a_1\cdots a_k){\leqslant} z\lt P^-(Q(\ell))$
, and so the inner sum
$P^+(a_1\cdots a_k){\leqslant} z\lt P^-(Q(\ell))$
, and so the inner sum
![]() $\Sigma$
of S is taken over integers
$\Sigma$
of S is taken over integers
![]() $\ell$
for which
$\ell$
for which
![]() $(Q(\ell),a_1\cdots a_k)=1$
. Moreover, since
$(Q(\ell),a_1\cdots a_k)=1$
. Moreover, since
![]() $z{\geqslant} k$
, we also have that
$z{\geqslant} k$
, we also have that
![]() $P^-(Q(\ell))\gt z{\geqslant} k$
, and this imposes the condition
$P^-(Q(\ell))\gt z{\geqslant} k$
, and this imposes the condition
![]() $(Q(\ell),\prod_{p{\leqslant} k}p)=1$
on
$(Q(\ell),\prod_{p{\leqslant} k}p)=1$
on
![]() $\Sigma$
. According to the above, we can add the supplementary condition
$\Sigma$
. According to the above, we can add the supplementary condition
![]() $(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1$
to the inner sum
$(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1$
to the inner sum
![]() $\Sigma$
of (4·19). Therefore,
$\Sigma$
of (4·19). Therefore,
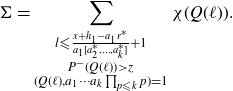 \begin{align}\Sigma = \sum_{\substack{l {\leqslant} \frac{x+h_1-a_{1}r^*}{a_{1}[a_{2}^*, \ldots, a_{k}^*]}+1 \\ P^{-}(Q(\ell))\gt z\\(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\chi(Q(\ell)).\end{align}
\begin{align}\Sigma = \sum_{\substack{l {\leqslant} \frac{x+h_1-a_{1}r^*}{a_{1}[a_{2}^*, \ldots, a_{k}^*]}+1 \\ P^{-}(Q(\ell))\gt z\\(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\chi(Q(\ell)).\end{align}
We now detect the sifting condition
![]() $P^-(Q(\ell))\gt z$
of (5·20) by applying Lemma 3·3 with
$P^-(Q(\ell))\gt z$
of (5·20) by applying Lemma 3·3 with
![]() $\beta=25k$
and
$\beta=25k$
and
![]() $u={\varepsilon} V/(30kv)$
. Since
$u={\varepsilon} V/(30kv)$
. Since
![]() $V {\geqslant} \frac{1}{2}+\varepsilon$
and
$V {\geqslant} \frac{1}{2}+\varepsilon$
and
![]() $\eta$
is large, we observe that
$\eta$
is large, we observe that
![]() $u={\varepsilon} V/(30vk){\geqslant} 50k$
. Hence,
$u={\varepsilon} V/(30vk){\geqslant} 50k$
. Hence,
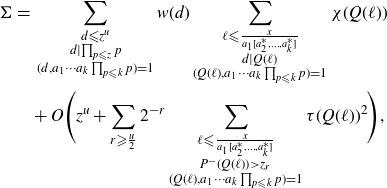 \begin{align}\begin{split}\Sigma =&\, \sum_{\substack{d {\leqslant} z^{u}\\ d\mid\prod_{p{\leqslant} z}p \\ (d,a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}w(d)\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ d|Q(\ell) \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\chi(Q(\ell)) \\&+O\Bigg(z^u+ \sum_{r {\geqslant} \frac{u}{2}}2^{-r}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2} \Bigg),\end{split}\end{align}
\begin{align}\begin{split}\Sigma =&\, \sum_{\substack{d {\leqslant} z^{u}\\ d\mid\prod_{p{\leqslant} z}p \\ (d,a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}w(d)\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ d|Q(\ell) \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\chi(Q(\ell)) \\&+O\Bigg(z^u+ \sum_{r {\geqslant} \frac{u}{2}}2^{-r}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2} \Bigg),\end{split}\end{align}
where
![]() $z_r = z^{((25k-1)/(25k))^r},$
and w is the arithmetic function from the statement of Lemma 3·3.
$z_r = z^{((25k-1)/(25k))^r},$
and w is the arithmetic function from the statement of Lemma 3·3.
5·1. Evaluation of the main term of
 $\Sigma$
in (5·21)
$\Sigma$
in (5·21)
We seek a bound for
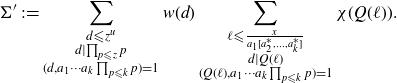 \begin{align*}\Sigma' \,:\!= \sum_{\substack{d {\leqslant} z^{u}\\ d\mid\prod_{p{\leqslant} z}p \\ (d,a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}w(d)\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ d|Q(\ell) \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\chi(Q(\ell)).\end{align*}
\begin{align*}\Sigma' \,:\!= \sum_{\substack{d {\leqslant} z^{u}\\ d\mid\prod_{p{\leqslant} z}p \\ (d,a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}w(d)\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ d|Q(\ell) \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\chi(Q(\ell)).\end{align*}
We spot the condition
![]() $(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1$
using Möbius inversion, so we obtain
$(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1$
using Möbius inversion, so we obtain
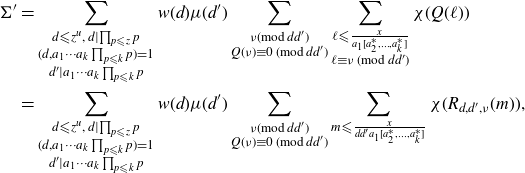 \begin{align}\begin{split}\Sigma' &= \sum_{\substack{d {\leqslant} z^{u},\, d\mid\prod_{p{\leqslant} z}p \\ (d,a_1\cdots a_k\prod_{p {\leqslant} k} p)=1 \\ d'|a_1\cdots a_k\prod_{p {\leqslant} k} p}}w(d)\mu(d')\sum_{\substack{\nu (\mathrm{mod}\,{dd'}) \\ Q(\nu) \equiv 0\, (\mathrm{mod}\,{dd'})}}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ \ell \equiv \nu\,( \mathrm{mod}\,{dd'} )}} \chi(Q(\ell)) \\&= \sum_{\substack{d {\leqslant} z^{u},\, d\mid\prod_{p{\leqslant} z}p \\ (d,a_1\cdots a_k\prod_{p {\leqslant} k} p)=1 \\ d'|a_1\cdots a_k\prod_{p {\leqslant} k} p}}w(d)\mu(d')\sum_{\substack{\nu( \mathrm{mod}\,{dd'}) \\ Q(\nu) \equiv 0\,( \mathrm{mod}\,{dd'})}}\sum_{m {\leqslant} \frac{x}{dd'a_1[a_2^*,\ldots,a_k^*]}} \chi(R_{d,d',\nu}(m)),\end{split}\end{align}
\begin{align}\begin{split}\Sigma' &= \sum_{\substack{d {\leqslant} z^{u},\, d\mid\prod_{p{\leqslant} z}p \\ (d,a_1\cdots a_k\prod_{p {\leqslant} k} p)=1 \\ d'|a_1\cdots a_k\prod_{p {\leqslant} k} p}}w(d)\mu(d')\sum_{\substack{\nu (\mathrm{mod}\,{dd'}) \\ Q(\nu) \equiv 0\, (\mathrm{mod}\,{dd'})}}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ \ell \equiv \nu\,( \mathrm{mod}\,{dd'} )}} \chi(Q(\ell)) \\&= \sum_{\substack{d {\leqslant} z^{u},\, d\mid\prod_{p{\leqslant} z}p \\ (d,a_1\cdots a_k\prod_{p {\leqslant} k} p)=1 \\ d'|a_1\cdots a_k\prod_{p {\leqslant} k} p}}w(d)\mu(d')\sum_{\substack{\nu( \mathrm{mod}\,{dd'}) \\ Q(\nu) \equiv 0\,( \mathrm{mod}\,{dd'})}}\sum_{m {\leqslant} \frac{x}{dd'a_1[a_2^*,\ldots,a_k^*]}} \chi(R_{d,d',\nu}(m)),\end{split}\end{align}
where
![]() $R_{d,d',\nu}\in{\mathbb{Z}}[X]$
with
$R_{d,d',\nu}\in{\mathbb{Z}}[X]$
with
![]() $R_{d,d',\nu}(X)\,:\!=Q(dd'X+\nu)$
.
$R_{d,d',\nu}(X)\,:\!=Q(dd'X+\nu)$
.
We want to apply Lemma 3·5 to bound the innermost character sum in (5·22). In order to do this with
![]() $q^*\ll (dd',q)$
, we have to verify that
$q^*\ll (dd',q)$
, we have to verify that
![]() $R_{d,d',\nu}$
is not a constant multiple of a square polynomial modulo p for primes
$R_{d,d',\nu}$
is not a constant multiple of a square polynomial modulo p for primes
![]() $p\nmid dd'$
with
$p\nmid dd'$
with
![]() $p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
and
$p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
and
![]() $p|q$
. We do this by considering the following complementary cases;
$p|q$
. We do this by considering the following complementary cases;
![]() $p \nmid a_i$
for all
$p \nmid a_i$
for all
![]() $i \in \{1,\ldots,k\}$
and
$i \in \{1,\ldots,k\}$
and
![]() $p | a_i$
for some
$p | a_i$
for some
![]() $i \in \{1,\ldots,k\}$
.
$i \in \{1,\ldots,k\}$
.
We first assume that
![]() $p \nmid a_i$
for all
$p \nmid a_i$
for all
![]() $i \in \{1,\ldots,k\}$
. In this case, if
$i \in \{1,\ldots,k\}$
. In this case, if
![]() $R_{d,d',\nu}$
is a square, then its roots have even multiplicity, which implies that there exist distinct indices
$R_{d,d',\nu}$
is a square, then its roots have even multiplicity, which implies that there exist distinct indices
![]() $i,j \in \{1,\ldots,k\}$
such that
$i,j \in \{1,\ldots,k\}$
such that
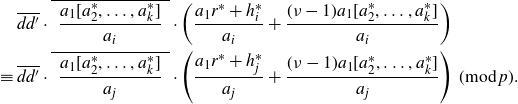 \begin{align*}&\,\overline{dd'}\cdot\overline{\,\,\frac{a_1[a_2^*,\ldots,a_k^*]}{a_i}\,\,}\cdot\left( \frac{a_1r^*+h_i^*}{a_i} + \frac{(\nu-1)a_1[a_2^*,\ldots,a_k^*]}{a_i} \right) \nonumber \\\equiv&\,\overline{dd'}\cdot\overline{\,\,\frac{a_1[a_2^*,\ldots,a_k^*]}{a_j}\,\,}\cdot\left( \frac{a_1r^*+h_j^*}{a_j} + \frac{(\nu-1)a_1[a_2^*,\ldots,a_k^*]}{a_j} \right) \; (\mathrm{mod}\,{p}).\end{align*}
\begin{align*}&\,\overline{dd'}\cdot\overline{\,\,\frac{a_1[a_2^*,\ldots,a_k^*]}{a_i}\,\,}\cdot\left( \frac{a_1r^*+h_i^*}{a_i} + \frac{(\nu-1)a_1[a_2^*,\ldots,a_k^*]}{a_i} \right) \nonumber \\\equiv&\,\overline{dd'}\cdot\overline{\,\,\frac{a_1[a_2^*,\ldots,a_k^*]}{a_j}\,\,}\cdot\left( \frac{a_1r^*+h_j^*}{a_j} + \frac{(\nu-1)a_1[a_2^*,\ldots,a_k^*]}{a_j} \right) \; (\mathrm{mod}\,{p}).\end{align*}
We multiply both sides of this congruence by
![]() $dd'(a_1[a_2^*,\ldots,a_k^*])^{2}a_i^{-1}a_j^{-1}$
and infer that
$dd'(a_1[a_2^*,\ldots,a_k^*])^{2}a_i^{-1}a_j^{-1}$
and infer that
Since
![]() $p \nmid a_i$
for all
$p \nmid a_i$
for all
![]() $i\in\{1,\ldots,k\}$
, we get
$i\in\{1,\ldots,k\}$
, we get
![]() $h_i^* \equiv h_j^*\;(\mathrm{mod}\,{p})$
, which is equivalent to
$h_i^* \equiv h_j^*\;(\mathrm{mod}\,{p})$
, which is equivalent to
![]() $h_i \equiv h_j \; (\mathrm{mod}\,{p})$
. But, since
$h_i \equiv h_j \; (\mathrm{mod}\,{p})$
. But, since
![]() $h_i,h_j {\leqslant} \max_{1 {\leqslant} \kappa {\leqslant} k} h_\kappa \lt p$
, we conclude that
$h_i,h_j {\leqslant} \max_{1 {\leqslant} \kappa {\leqslant} k} h_\kappa \lt p$
, we conclude that
![]() $h_i = h_j$
, which is a contradiction for
$h_i = h_j$
, which is a contradiction for
![]() $i \not= j$
as the shifts
$i \not= j$
as the shifts
![]() $h_1,\ldots,h_k$
are distinct. Consequently,
$h_1,\ldots,h_k$
are distinct. Consequently,
![]() $R_{d,d',\nu}$
is not a constant multiple of a square polynomial modulo p in this case.
$R_{d,d',\nu}$
is not a constant multiple of a square polynomial modulo p in this case.
We now assume that
![]() $p | a_i$
for some
$p | a_i$
for some
![]() $i \in \{1,\ldots,k\}$
. This implies that
$i \in \{1,\ldots,k\}$
. This implies that
![]() $p \nmid a_j$
for all
$p \nmid a_j$
for all
![]() $j \not= i$
, otherwise
$j \not= i$
, otherwise
![]() $p|(a_i,a_j)$
for some
$p|(a_i,a_j)$
for some
![]() $j\not=i$
, which, combined with the condition
$j\not=i$
, which, combined with the condition
![]() $(a_i,a_j)|(h_i-h_j)$
of (4·19), would imply the divisibility relation
$(a_i,a_j)|(h_i-h_j)$
of (4·19), would imply the divisibility relation
![]() $p|(h_i-h_j)$
which contradicts the condition
$p|(h_i-h_j)$
which contradicts the condition
![]() $p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
that we are working under. By the same argument, if
$p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
that we are working under. By the same argument, if
![]() $i\neq 1$
, then we can deduce that
$i\neq 1$
, then we can deduce that
![]() $p\mid a_i^*$
. Combining both our conclusions, we observe that p divides
$p\mid a_i^*$
. Combining both our conclusions, we observe that p divides
![]() $a_{1,j}[a_2^*,\ldots,a_k^*]{a_{j}^*}^{-1}=a_1[a_2^*,\ldots,a_k^*]{a_j}^{-1}$
for
$a_{1,j}[a_2^*,\ldots,a_k^*]{a_{j}^*}^{-1}=a_1[a_2^*,\ldots,a_k^*]{a_j}^{-1}$
for
![]() $j\neq i$
. Note also that
$j\neq i$
. Note also that
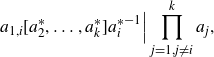 $$ a_{1,i}[a_2^*,\ldots,a_k^*]{a_{i}^*}^{-1}\Big| \prod_{\substack{j=1, j \not= i}}^{k} a_j,$$
$$ a_{1,i}[a_2^*,\ldots,a_k^*]{a_{i}^*}^{-1}\Big| \prod_{\substack{j=1, j \not= i}}^{k} a_j,$$
because
![]() $[a_2^*,\ldots,a_k^*]$
divides
$[a_2^*,\ldots,a_k^*]$
divides
![]() $a_2^*\cdots a_k^*$
, which in turn divides
$a_2^*\cdots a_k^*$
, which in turn divides
![]() $a_2\cdots a_k$
. So,
$a_2\cdots a_k$
. So,
![]() $p\nmid a_{1,i}[a_2^*,\ldots,a_k^*]{a_{i}^*}^{-1}$
, whereas
$p\nmid a_{1,i}[a_2^*,\ldots,a_k^*]{a_{i}^*}^{-1}$
, whereas
![]() $p\mid a_{1,j}[a_2^*,\ldots,a_k^*]{a_{j}^*}^{-1}$
for
$p\mid a_{1,j}[a_2^*,\ldots,a_k^*]{a_{j}^*}^{-1}$
for
![]() $j\neq i$
. We thus see that
$j\neq i$
. We thus see that
![]() $R_{d,d',\nu}(X)\equiv c_1X+c_0 \mathrm{mod}\,{p}$
for some
$R_{d,d',\nu}(X)\equiv c_1X+c_0 \mathrm{mod}\,{p}$
for some
![]() $c_0,c_1 \in {\mathbb{N}}$
, which shows that
$c_0,c_1 \in {\mathbb{N}}$
, which shows that
![]() $R_{d,d',\nu}$
is not a constant multiple of a square polynomial modulo p in this case either.
$R_{d,d',\nu}$
is not a constant multiple of a square polynomial modulo p in this case either.
Now that we have concluded that
![]() $R_{d,d',\nu}$
is not a constant multiple of a square polynomial modulo p when p is a prime such that
$R_{d,d',\nu}$
is not a constant multiple of a square polynomial modulo p when p is a prime such that
![]() $p|q$
,
$p|q$
,
![]() $p\nmid dd'$
and
$p\nmid dd'$
and
![]() $p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
, Lemma 3·5 yields
$p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
, Lemma 3·5 yields
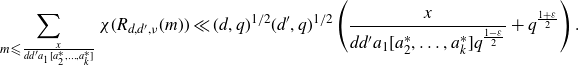 \begin{align}\sum_{m {\leqslant} \frac{x}{dd'a_1[a_2^*,\ldots,a_k^*]}} \chi(R_{d,d',\nu}(m)) \ll(d,q)^{1/2}(d',q)^{1/2}\left(\frac{x}{dd'a_1[a_2^*,\ldots,a_k^*]q^{\frac{1-{\varepsilon}}{2}}} +q^{\frac{1+{\varepsilon}}{2}} \right).\end{align}
\begin{align}\sum_{m {\leqslant} \frac{x}{dd'a_1[a_2^*,\ldots,a_k^*]}} \chi(R_{d,d',\nu}(m)) \ll(d,q)^{1/2}(d',q)^{1/2}\left(\frac{x}{dd'a_1[a_2^*,\ldots,a_k^*]q^{\frac{1-{\varepsilon}}{2}}} +q^{\frac{1+{\varepsilon}}{2}} \right).\end{align}
Using Lemma 3·6 and the condition
![]() $(a_i,a_j)|(h_i-h_j)$
from the outermost sum of (4·19), we find that
$(a_i,a_j)|(h_i-h_j)$
from the outermost sum of (4·19), we find that
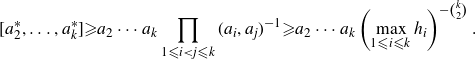 \begin{align}[a_2^*,\ldots,a_k^*] {\geqslant} a_2\cdots a_k \prod_{1{\leqslant} i \lt j {\leqslant} k}(a_i,a_j)^{-1} {\geqslant} a_2\cdots a_k\left( \max_{1 {\leqslant} i {\leqslant} k} h_i \right)^{-\binom{k}{2}}.\end{align}
\begin{align}[a_2^*,\ldots,a_k^*] {\geqslant} a_2\cdots a_k \prod_{1{\leqslant} i \lt j {\leqslant} k}(a_i,a_j)^{-1} {\geqslant} a_2\cdots a_k\left( \max_{1 {\leqslant} i {\leqslant} k} h_i \right)^{-\binom{k}{2}}.\end{align}
We combine (5·23) and (5·24). Hence, since d and d’ are coprime and the arithmetic function
![]() $\rho$
defined as
$\rho$
defined as
![]() $\rho(m)\,:\!=\{\nu\;(\mathrm{mod}\,{m})\,:\,Q(\nu)\equiv0\;(\mathrm{mod}\,{m})\}$
for all
$\rho(m)\,:\!=\{\nu\;(\mathrm{mod}\,{m})\,:\,Q(\nu)\equiv0\;(\mathrm{mod}\,{m})\}$
for all
![]() $m\in{\mathbb{N}}$
is multiplicative (by the Chinese Remainder Theorem), (5·22) gives
$m\in{\mathbb{N}}$
is multiplicative (by the Chinese Remainder Theorem), (5·22) gives
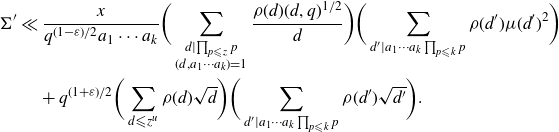 \begin{align}\begin{split}\Sigma'\ll&\,\frac{x}{q^{(1-{\varepsilon})/2}a_1\cdots a_k}\bigg(\sum_{\substack{d\mid\prod_{p{\leqslant} z}p\\(d,a_1\cdots a_k)=1}}\frac{\rho(d)(d,q)^{1/2}}{d}\bigg)\bigg(\sum_{d'\mid a_1\cdots a_k\prod_{p{\leqslant} k}p}\rho(d')\mu(d')^2\bigg)\\&+q^{(1+{\varepsilon})/2}\bigg(\sum_{d{\leqslant} z^u}\rho(d)\sqrt{d}\bigg)\bigg(\sum_{d'\mid a_1\cdots a_k\prod_{p{\leqslant} k}p}\rho(d')\sqrt{d'}\bigg).\end{split}\end{align}
\begin{align}\begin{split}\Sigma'\ll&\,\frac{x}{q^{(1-{\varepsilon})/2}a_1\cdots a_k}\bigg(\sum_{\substack{d\mid\prod_{p{\leqslant} z}p\\(d,a_1\cdots a_k)=1}}\frac{\rho(d)(d,q)^{1/2}}{d}\bigg)\bigg(\sum_{d'\mid a_1\cdots a_k\prod_{p{\leqslant} k}p}\rho(d')\mu(d')^2\bigg)\\&+q^{(1+{\varepsilon})/2}\bigg(\sum_{d{\leqslant} z^u}\rho(d)\sqrt{d}\bigg)\bigg(\sum_{d'\mid a_1\cdots a_k\prod_{p{\leqslant} k}p}\rho(d')\sqrt{d'}\bigg).\end{split}\end{align}
Using the trivial inequalities
![]() $\tau(m),\rho(m){\leqslant} m$
for all
$\tau(m),\rho(m){\leqslant} m$
for all
![]() $m\in{\mathbb{N}}$
, we immediately derive the bound
$m\in{\mathbb{N}}$
, we immediately derive the bound
as well as the estimate
Consequently, after recalling that
![]() $a_1,\ldots,a_k{\leqslant} z^u$
in the expression (4·19) of S, (5·25) implies
$a_1,\ldots,a_k{\leqslant} z^u$
in the expression (4·19) of S, (5·25) implies
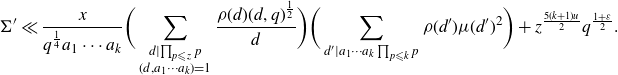 \begin{align}\Sigma'\ll&\,\frac{x}{q^{\frac{1}{4}}a_1\cdots a_k}\bigg(\sum_{\substack{d\mid\prod_{p{\leqslant} z}p\\(d,a_1\cdots a_k)=1}}\frac{\rho(d)(d,q)^{\frac{1}{2}}}{d}\bigg)\bigg(\sum_{d'\mid a_1\cdots a_k\prod_{p{\leqslant} k}p}\rho(d')\mu(d')^2\bigg)+z^{\frac{5(k+1)u}{2}}q^{\frac{1+{\varepsilon}}{2}}.\end{align}
\begin{align}\Sigma'\ll&\,\frac{x}{q^{\frac{1}{4}}a_1\cdots a_k}\bigg(\sum_{\substack{d\mid\prod_{p{\leqslant} z}p\\(d,a_1\cdots a_k)=1}}\frac{\rho(d)(d,q)^{\frac{1}{2}}}{d}\bigg)\bigg(\sum_{d'\mid a_1\cdots a_k\prod_{p{\leqslant} k}p}\rho(d')\mu(d')^2\bigg)+z^{\frac{5(k+1)u}{2}}q^{\frac{1+{\varepsilon}}{2}}.\end{align}
We previously noted that any two roots of the polynomial
![]() $R_{d,d',\nu}$
cannot be congruent modulo p. By an almost identical approach, for the primes
$R_{d,d',\nu}$
cannot be congruent modulo p. By an almost identical approach, for the primes
![]() $p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
that do not divide the product
$p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
that do not divide the product
![]() $a_1\cdots a_k$
, one can show that the k roots
$a_1\cdots a_k$
, one can show that the k roots
of Q modulo p are distinct. Thus,
![]() $\rho(p)=k$
for every prime
$\rho(p)=k$
for every prime
![]() $p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
which does not divide
$p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
which does not divide
![]() $a_1\cdots a_k$
. Furthermore, if
$a_1\cdots a_k$
. Furthermore, if
![]() $p\mid a_1\cdots a_k$
, then Q reduces to a constant or first degree polynomial modulo p. Therefore, for the primes
$p\mid a_1\cdots a_k$
, then Q reduces to a constant or first degree polynomial modulo p. Therefore, for the primes
![]() $p\mid a_1\cdots a_k$
, we have that
$p\mid a_1\cdots a_k$
, we have that
![]() $\rho(p){\leqslant} 1$
. We are going to use these two observations to bound the sums at (5·26). Firstly, we have that
$\rho(p){\leqslant} 1$
. We are going to use these two observations to bound the sums at (5·26). Firstly, we have that
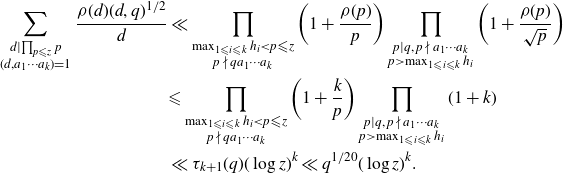 \begin{align}\begin{split}\sum_{\substack{d\mid\prod_{p{\leqslant} z}p\\(d,a_1\cdots a_k)=1}}\frac{\rho(d)(d,q)^{1/2}}{d}&\ll \prod_{\substack{\max_{1 {\leqslant} i {\leqslant} k} h_i\lt p{\leqslant} z\\p\,\nmid\, qa_1\cdots a_k}}\bigg(1+\frac{\rho(p)}{p}\bigg)\prod_{\substack{p\mid q,\,p\,\nmid\,a_1\cdots a_k\\p\gt \max_{1 {\leqslant} i {\leqslant} k} h_i}}\bigg(1+\frac{\rho(p)}{\sqrt{p}}\bigg) \\&{\leqslant}\prod_{\substack{\max_{1 {\leqslant} i {\leqslant} k} h_i\lt p{\leqslant} z\\p\,\nmid\, qa_1\cdots a_k}}\bigg(1+\frac{k}{p}\bigg)\prod_{\substack{p\mid q,\,p\,\nmid\,a_1\cdots a_k\\p\gt \max_{1 {\leqslant} i {\leqslant} k} h_i}}(1+k) \\&\ll \tau_{k+1}(q)(\log z)^k \ll q^{1/20}(\log z)^k.\end{split}\end{align}
\begin{align}\begin{split}\sum_{\substack{d\mid\prod_{p{\leqslant} z}p\\(d,a_1\cdots a_k)=1}}\frac{\rho(d)(d,q)^{1/2}}{d}&\ll \prod_{\substack{\max_{1 {\leqslant} i {\leqslant} k} h_i\lt p{\leqslant} z\\p\,\nmid\, qa_1\cdots a_k}}\bigg(1+\frac{\rho(p)}{p}\bigg)\prod_{\substack{p\mid q,\,p\,\nmid\,a_1\cdots a_k\\p\gt \max_{1 {\leqslant} i {\leqslant} k} h_i}}\bigg(1+\frac{\rho(p)}{\sqrt{p}}\bigg) \\&{\leqslant}\prod_{\substack{\max_{1 {\leqslant} i {\leqslant} k} h_i\lt p{\leqslant} z\\p\,\nmid\, qa_1\cdots a_k}}\bigg(1+\frac{k}{p}\bigg)\prod_{\substack{p\mid q,\,p\,\nmid\,a_1\cdots a_k\\p\gt \max_{1 {\leqslant} i {\leqslant} k} h_i}}(1+k) \\&\ll \tau_{k+1}(q)(\log z)^k \ll q^{1/20}(\log z)^k.\end{split}\end{align}
We also have
We now insert (5·27) and (5·28) into (5·26) to complete the estimation of
![]() $\Sigma'$
. This way we obtain
$\Sigma'$
. This way we obtain
5·2. Evaluation of the error term of
 $\Sigma$
in (5·21)
$\Sigma$
in (5·21)
Upon denoting the Big-Oh term of (5·21) by
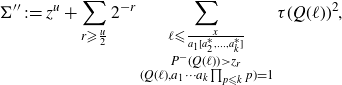 \begin{equation}\Sigma'' \,:\!= z^u+\sum_{r {\geqslant} \frac{u}{2}}2^{-r}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2},\end{equation}
\begin{equation}\Sigma'' \,:\!= z^u+\sum_{r {\geqslant} \frac{u}{2}}2^{-r}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2},\end{equation}
the next step of the proof is to bound
![]() $\Sigma''$
. We basically achieve this with an application of Lemma 3·4 to the divisor sum of
$\Sigma''$
. We basically achieve this with an application of Lemma 3·4 to the divisor sum of
![]() $\Sigma''$
.
$\Sigma''$
.
The inequality
![]() $\tau(ab) {\leqslant} \tau(a)\tau(b)$
which holds for any
$\tau(ab) {\leqslant} \tau(a)\tau(b)$
which holds for any
![]() $a,b \in {\mathbb{N}}$
implies that
$a,b \in {\mathbb{N}}$
implies that
 \begin{equation}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]}\\ P^{-}(Q(\ell))\gt z_r\\(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2}{\leqslant} \sum_{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]}}F(Q_1(\ell),\ldots,Q_k(\ell)),\end{equation}
\begin{equation}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]}\\ P^{-}(Q(\ell))\gt z_r\\(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2}{\leqslant} \sum_{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]}}F(Q_1(\ell),\ldots,Q_k(\ell)),\end{equation}
where
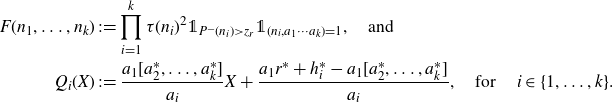 \begin{align*}F(n_1,\ldots,n_k) &\,:\!= \prod_{i=1}^{k}\tau(n_i)^2{\unicode{x1D7D9}}_{P^{-}(n_i)\gt z_r}{\unicode{x1D7D9}}_{(n_i,a_1\cdots a_k)=1},\quad \text{and}\\Q_{i}(X) &\,:\!= \frac{a_1[a_2^*,\ldots,a_k^*]}{a_i}X+\frac{a_1r^*+h_i^*-a_1[a_2^*,\ldots,a_k^*]}{a_i},\quad \text{for }\quad i \in \{1,\ldots,k\}.\end{align*}
\begin{align*}F(n_1,\ldots,n_k) &\,:\!= \prod_{i=1}^{k}\tau(n_i)^2{\unicode{x1D7D9}}_{P^{-}(n_i)\gt z_r}{\unicode{x1D7D9}}_{(n_i,a_1\cdots a_k)=1},\quad \text{and}\\Q_{i}(X) &\,:\!= \frac{a_1[a_2^*,\ldots,a_k^*]}{a_i}X+\frac{a_1r^*+h_i^*-a_1[a_2^*,\ldots,a_k^*]}{a_i},\quad \text{for }\quad i \in \{1,\ldots,k\}.\end{align*}
We now aim to apply Lemma 3·4 to the right-hand side of (5·31) as this will lead to a bound for
![]() $\Sigma''$
. In order to use Lemma 3·4, we verify that all of its conditions are met. First of all, the polynomials
$\Sigma''$
. In order to use Lemma 3·4, we verify that all of its conditions are met. First of all, the polynomials
![]() $Q_1,\ldots,Q_k$
are irreducible and pairwise coprime because they are linear and have distinct roots. Now, suppose that
$Q_1,\ldots,Q_k$
are irreducible and pairwise coprime because they are linear and have distinct roots. Now, suppose that
![]() $Q=Q_1\cdots Q_k$
has a fixed prime divisor p, or that we equivalently have that
$Q=Q_1\cdots Q_k$
has a fixed prime divisor p, or that we equivalently have that
![]() $\rho(p)=p$
. If
$\rho(p)=p$
. If
![]() $p|a_1\cdots a_k$
, then the fixed prime divisor p of Q divides
$p|a_1\cdots a_k$
, then the fixed prime divisor p of Q divides
![]() $a_1, \ldots, a_k$
. However, in this case, the condition
$a_1, \ldots, a_k$
. However, in this case, the condition
![]() $(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1$
in (5·30) is not satisfied for any
$(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1$
in (5·30) is not satisfied for any
![]() $\ell \in {\mathbb{N}}$
, and
$\ell \in {\mathbb{N}}$
, and
![]() $\Sigma''=0$
. If
$\Sigma''=0$
. If
![]() $p\nmid a_1\cdots a_k$
, then Q is a polynomial of degree k. This implies that
$p\nmid a_1\cdots a_k$
, then Q is a polynomial of degree k. This implies that
![]() $p = \rho(p) {\leqslant} k$
, and so, in this case, Q has a fixed prime divisor
$p = \rho(p) {\leqslant} k$
, and so, in this case, Q has a fixed prime divisor
![]() $p {\leqslant} k$
. Then the condition
$p {\leqslant} k$
. Then the condition
![]() $(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1$
in (5·30) is not met for any
$(Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1$
in (5·30) is not met for any
![]() $\ell \in {\mathbb{N}}$
and
$\ell \in {\mathbb{N}}$
and
![]() $\Sigma''$
vanishes again. Hence, if Q has a fixed prime divisor, then
$\Sigma''$
vanishes again. Hence, if Q has a fixed prime divisor, then
![]() $\Sigma''=0$
and there is nothing to bound. Therefore, we may assume that Q has no fixed prime factors. Finally, by combining
$\Sigma''=0$
and there is nothing to bound. Therefore, we may assume that Q has no fixed prime factors. Finally, by combining
![]() $z^{30ku} = x^{{\varepsilon}}$
, which is an immediate consequence of the definition of u, with the inequalities
$z^{30ku} = x^{{\varepsilon}}$
, which is an immediate consequence of the definition of u, with the inequalities
![]() $r^*{\leqslant} [a_2^*,\ldots,a_k^*]{\leqslant} a_2\cdots a_k$
and
$r^*{\leqslant} [a_2^*,\ldots,a_k^*]{\leqslant} a_2\cdots a_k$
and
![]() $a_1,\ldots,a_k{\leqslant} z^u$
, we observe that
$a_1,\ldots,a_k{\leqslant} z^u$
, we observe that
where
![]() $\Vert Q \Vert$
denotes the sum of the absolute values of the coefficients of the polynomial Q.
$\Vert Q \Vert$
denotes the sum of the absolute values of the coefficients of the polynomial Q.
Now that we finished verifying that Henriot’s bound, namely Lemma 3·4, is applicable, we apply it to the right-hand side of (5·31) and obtain that
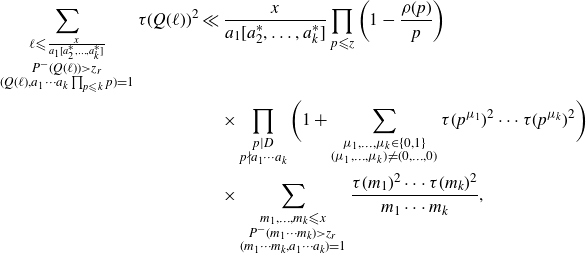 \begin{align}\begin{split}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2} \ll&\, \frac{x}{a_1[a_2^*,\ldots,a_k^*]}\prod_{p{\leqslant} z}\left( 1-\frac{\rho(p)}{p} \right) \\&\times \prod_{\substack{p|D \\ p \nmid a_1\cdots a_k}}\bigg( 1 + \sum_{\substack{\mu_1, \ldots, \mu_k \in \{0,1\} \\ (\mu_1,\ldots,\mu_k) \not= (0,\ldots,0)}} \tau(p^{\mu_1})^2\cdots\tau(p^{\mu_k})^2 \bigg) \\&\times \sum_{\substack{m_1,\ldots,m_k {\leqslant} x \\ P^{-}(m_1\cdots m_k)\gt z_r \\ (m_1\cdots m_k,a_1\cdots a_k)=1}}\frac{\tau(m_1)^2\cdots\tau(m_k)^2}{m_1\cdots m_k},\end{split}\end{align}
\begin{align}\begin{split}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2} \ll&\, \frac{x}{a_1[a_2^*,\ldots,a_k^*]}\prod_{p{\leqslant} z}\left( 1-\frac{\rho(p)}{p} \right) \\&\times \prod_{\substack{p|D \\ p \nmid a_1\cdots a_k}}\bigg( 1 + \sum_{\substack{\mu_1, \ldots, \mu_k \in \{0,1\} \\ (\mu_1,\ldots,\mu_k) \not= (0,\ldots,0)}} \tau(p^{\mu_1})^2\cdots\tau(p^{\mu_k})^2 \bigg) \\&\times \sum_{\substack{m_1,\ldots,m_k {\leqslant} x \\ P^{-}(m_1\cdots m_k)\gt z_r \\ (m_1\cdots m_k,a_1\cdots a_k)=1}}\frac{\tau(m_1)^2\cdots\tau(m_k)^2}{m_1\cdots m_k},\end{split}\end{align}
where D is the discriminant of Q.
The value of D can be easily evaluated by the roots of Q and a simple calculation shows that
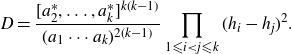 \begin{align*}D = \frac{[a_2^*,\ldots,a_k^*]^{k(k-1)}}{(a_1\cdots a_k)^{2(k-1)}}\prod_{1 {\leqslant} i \lt j {\leqslant} k}(h_i-h_j)^{2}.\end{align*}
\begin{align*}D = \frac{[a_2^*,\ldots,a_k^*]^{k(k-1)}}{(a_1\cdots a_k)^{2(k-1)}}\prod_{1 {\leqslant} i \lt j {\leqslant} k}(h_i-h_j)^{2}.\end{align*}
Since we are working with a fixed set of non-negative integers
![]() $h_1,\ldots,h_k$
, we see from this that
$h_1,\ldots,h_k$
, we see from this that
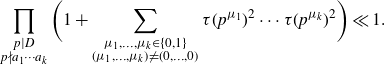 \begin{align}\prod_{\substack{p|D \\ p \nmid a_1\cdots a_k}}\bigg( 1 + \sum_{\substack{\mu_1, \ldots, \mu_k \in \{0,1\}\\ (\mu_1,\ldots,\mu_k) \not= (0,\ldots,0)}} \tau(p^{\mu_1})^2\cdots\tau(p^{\mu_k})^2 \bigg) \ll 1.\end{align}
\begin{align}\prod_{\substack{p|D \\ p \nmid a_1\cdots a_k}}\bigg( 1 + \sum_{\substack{\mu_1, \ldots, \mu_k \in \{0,1\}\\ (\mu_1,\ldots,\mu_k) \not= (0,\ldots,0)}} \tau(p^{\mu_1})^2\cdots\tau(p^{\mu_k})^2 \bigg) \ll 1.\end{align}
We saw that
![]() $\rho(p)=k$
for the primes
$\rho(p)=k$
for the primes
![]() $p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
which do not divide
$p \gt \max_{1 {\leqslant} i {\leqslant} k} h_i$
which do not divide
![]() $a_1\cdots a_k$
. Therefore, by Bernoulli’s inequality,
$a_1\cdots a_k$
. Therefore, by Bernoulli’s inequality,
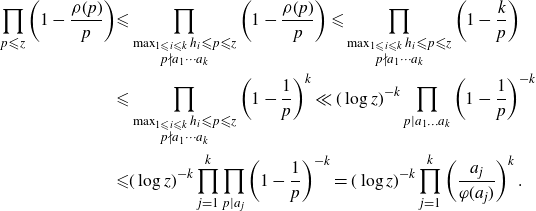 \begin{align}\begin{split}\prod_{p{\leqslant} z}\left( 1-\frac{\rho(p)}{p} \right) &{\leqslant} \prod_{\substack{\max_{1{\leqslant} i {\leqslant} k} h_i {\leqslant} p{\leqslant} z \\ p \nmid a_1\cdots a_k } }\left( 1-\frac{\rho(p)}{p} \right) {\leqslant} \prod_{\substack{\max_{1{\leqslant} i {\leqslant} k} h_i {\leqslant} p{\leqslant} z \\ p \nmid a_1\cdots a_k } }\left( 1-\frac{k}{p} \right) \\&{\leqslant} \prod_{\substack{\max_{1{\leqslant} i {\leqslant} k} h_i {\leqslant} p{\leqslant} z \\ p \nmid a_1\cdots a_k } }\left( 1-\frac{1}{p} \right)^{k} \ll (\log{z})^{-k}\prod_{p | a_1\ldots a_k}\left(1-\frac{1}{p}\right)^{-k} \\&{\leqslant} (\log{z})^{-k}\prod_{j=1}^{k}\prod_{p | a_j}\left(1-\frac{1}{p}\right)^{-k}= (\log{z})^{-k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}. \end{split}\end{align}
\begin{align}\begin{split}\prod_{p{\leqslant} z}\left( 1-\frac{\rho(p)}{p} \right) &{\leqslant} \prod_{\substack{\max_{1{\leqslant} i {\leqslant} k} h_i {\leqslant} p{\leqslant} z \\ p \nmid a_1\cdots a_k } }\left( 1-\frac{\rho(p)}{p} \right) {\leqslant} \prod_{\substack{\max_{1{\leqslant} i {\leqslant} k} h_i {\leqslant} p{\leqslant} z \\ p \nmid a_1\cdots a_k } }\left( 1-\frac{k}{p} \right) \\&{\leqslant} \prod_{\substack{\max_{1{\leqslant} i {\leqslant} k} h_i {\leqslant} p{\leqslant} z \\ p \nmid a_1\cdots a_k } }\left( 1-\frac{1}{p} \right)^{k} \ll (\log{z})^{-k}\prod_{p | a_1\ldots a_k}\left(1-\frac{1}{p}\right)^{-k} \\&{\leqslant} (\log{z})^{-k}\prod_{j=1}^{k}\prod_{p | a_j}\left(1-\frac{1}{p}\right)^{-k}= (\log{z})^{-k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}. \end{split}\end{align}
Furthermore,
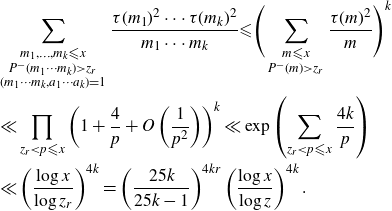 \begin{align}\begin{split}&\sum_{\substack{m_1,\ldots,m_k {\leqslant} x \\ P^{-}(m_1\cdots m_k)\gt z_r \\ (m_1\cdots m_k,a_1\cdots a_k)=1}}\frac{\tau(m_1)^2\cdots\tau(m_k)^2}{m_1\cdots m_k} {\leqslant} \Bigg( \sum_{\substack{m {\leqslant} x \\ P^{-}(m) \gt z_r}} \frac{\tau(m)^2}{m} \Bigg)^k \\&\ll \prod_{z_r \lt p {\leqslant} x}\left( 1+\frac{4}{p}+O\left( \frac{1}{p^2} \right) \right)^k \ll \exp\left( \sum_{z_r \lt p {\leqslant} x} \frac{4k}{p} \right) \\&\ll \left( \frac{\log{x}}{\log{z_r}} \right)^{4k}= \left( \frac{25k}{25k-1} \right)^{4kr}\left( \frac{\log{x}}{\log{z}} \right)^{4k}.\end{split}\end{align}
\begin{align}\begin{split}&\sum_{\substack{m_1,\ldots,m_k {\leqslant} x \\ P^{-}(m_1\cdots m_k)\gt z_r \\ (m_1\cdots m_k,a_1\cdots a_k)=1}}\frac{\tau(m_1)^2\cdots\tau(m_k)^2}{m_1\cdots m_k} {\leqslant} \Bigg( \sum_{\substack{m {\leqslant} x \\ P^{-}(m) \gt z_r}} \frac{\tau(m)^2}{m} \Bigg)^k \\&\ll \prod_{z_r \lt p {\leqslant} x}\left( 1+\frac{4}{p}+O\left( \frac{1}{p^2} \right) \right)^k \ll \exp\left( \sum_{z_r \lt p {\leqslant} x} \frac{4k}{p} \right) \\&\ll \left( \frac{\log{x}}{\log{z_r}} \right)^{4k}= \left( \frac{25k}{25k-1} \right)^{4kr}\left( \frac{\log{x}}{\log{z}} \right)^{4k}.\end{split}\end{align}
We insert the bounds (5·24), (5·33), (5·34) and (5·35) into (5·32) and obtain
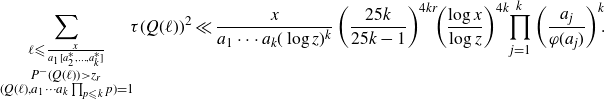 \begin{align*}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\!\!\tau(Q(\ell))^{2} \ll \frac{x}{a_1\cdots a_k (\log{z})^k}\left( \frac{25k}{25k-1} \right)^{4kr}\!\!\left( \frac{\log{x}}{\log{z}} \right)^{4k}\!\prod_{j=1}^{\!k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}\!\!.\end{align*}
\begin{align*}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\!\!\tau(Q(\ell))^{2} \ll \frac{x}{a_1\cdots a_k (\log{z})^k}\left( \frac{25k}{25k-1} \right)^{4kr}\!\!\left( \frac{\log{x}}{\log{z}} \right)^{4k}\!\prod_{j=1}^{\!k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}\!\!.\end{align*}
But, we note that
![]() $25k-1\gt 24k\gt 8k/(\log 4-1)$
, and so
$25k-1\gt 24k\gt 8k/(\log 4-1)$
, and so
Hence,
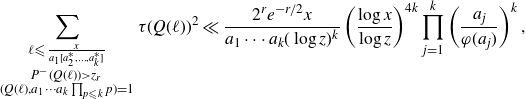 \begin{align*}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2} \ll \frac{2^re^{-r/2}x}{a_1\cdots a_k (\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k},\end{align*}
\begin{align*}\sum_{\substack{\ell {\leqslant} \frac{x}{a_1[a_2^*,\ldots,a_k^*]} \\ P^{-}(Q(\ell))\gt z_r \\ (Q(\ell),a_1\cdots a_k\prod_{p {\leqslant} k} p)=1}}\tau(Q(\ell))^{2} \ll \frac{2^re^{-r/2}x}{a_1\cdots a_k (\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k},\end{align*}
and then in virtue of (5·30), we obtain
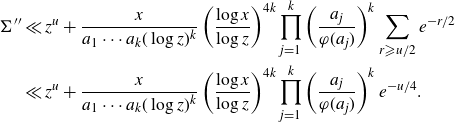 \begin{align}\begin{split}\Sigma'' &\ll z^u+\frac{x}{a_1\cdots a_k (\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}\sum_{r {\geqslant} u/2}e^{-r/2} \\&\ll z^u+\frac{x}{a_1\cdots a_k (\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}e^{-u/4}. \end{split}\end{align}
\begin{align}\begin{split}\Sigma'' &\ll z^u+\frac{x}{a_1\cdots a_k (\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}\sum_{r {\geqslant} u/2}e^{-r/2} \\&\ll z^u+\frac{x}{a_1\cdots a_k (\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}e^{-u/4}. \end{split}\end{align}
5·3 Completing the estimation of S in (4·14)
We now combine (5·29) with (5·36), and so (5·21) gives
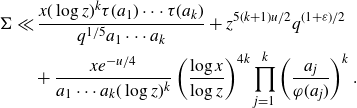 \begin{align*}\Sigma \ll&\, \frac{x(\log z)^k\tau(a_1)\cdots \tau(a_k)}{q^{1/5}a_1\cdots a_k} +z^{5(k+1)u/2}q^{(1+{\varepsilon})/2} \\&+ \frac{xe^{-u/4}}{a_1\cdots a_k (\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}.\end{align*}
\begin{align*}\Sigma \ll&\, \frac{x(\log z)^k\tau(a_1)\cdots \tau(a_k)}{q^{1/5}a_1\cdots a_k} +z^{5(k+1)u/2}q^{(1+{\varepsilon})/2} \\&+ \frac{xe^{-u/4}}{a_1\cdots a_k (\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}.\end{align*}
We finally insert this bound into (4·19) and obtain
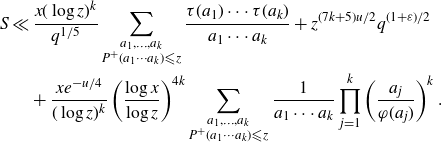 \begin{align}\begin{split}S \ll&\, \frac{x(\log z)^k}{q^{1/5}}\sum_{\substack{a_1,\ldots,a_k\\P^+(a_1\cdots a_k){\leqslant} z}}\frac{\tau(a_1)\cdots\tau(a_k)}{a_1\cdots a_k} +z^{(7k+5)u/2}q^{(1+{\varepsilon})/2}\\&+\frac{xe^{-u/4}}{(\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\sum_{\substack{a_1,\ldots,a_k \\P^{+}(a_1\cdots a_k){\leqslant} z} } \frac{1}{a_1\cdots a_k }\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}.\end{split}\end{align}
\begin{align}\begin{split}S \ll&\, \frac{x(\log z)^k}{q^{1/5}}\sum_{\substack{a_1,\ldots,a_k\\P^+(a_1\cdots a_k){\leqslant} z}}\frac{\tau(a_1)\cdots\tau(a_k)}{a_1\cdots a_k} +z^{(7k+5)u/2}q^{(1+{\varepsilon})/2}\\&+\frac{xe^{-u/4}}{(\log{z})^k}\left( \frac{\log{x}}{\log{z}} \right)^{4k}\sum_{\substack{a_1,\ldots,a_k \\P^{+}(a_1\cdots a_k){\leqslant} z} } \frac{1}{a_1\cdots a_k }\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k}.\end{split}\end{align}
But,
 \begin{align}\begin{split}&\sum_{\substack{a_1,\ldots,a_k \\P^{+}(a_1\cdots a_k){\leqslant} z} } \frac{1}{a_1\cdots a_k }\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k} {\leqslant} \Bigg( \sum_{\substack{ a \\P^{+}(a){\leqslant} z} } \frac{1}{a}\left( \frac{a}{\varphi(a)} \right)^k \Bigg)^k \\&{\leqslant} \prod_{p {\leqslant} z}\left( 1+\left( \frac{p}{p-1} \right)^k\frac{1}{p}+O\left( \frac{1}{p^2} \right) \right)^k \ll \exp\left( \sum_{p {\leqslant} z} \left( \frac{p}{p-1} \right)^k\frac{k}{p} \right) \\&=\exp\left\{ \sum_{p {\leqslant} z} \left( \frac{k}{p}+O\left( \frac{1}{p^2} \right) \right) \right\} \ll (\log{z})^k.\end{split}\end{align}
\begin{align}\begin{split}&\sum_{\substack{a_1,\ldots,a_k \\P^{+}(a_1\cdots a_k){\leqslant} z} } \frac{1}{a_1\cdots a_k }\prod_{j=1}^{k}\left( \frac{a_j}{\varphi(a_j)} \right)^{k} {\leqslant} \Bigg( \sum_{\substack{ a \\P^{+}(a){\leqslant} z} } \frac{1}{a}\left( \frac{a}{\varphi(a)} \right)^k \Bigg)^k \\&{\leqslant} \prod_{p {\leqslant} z}\left( 1+\left( \frac{p}{p-1} \right)^k\frac{1}{p}+O\left( \frac{1}{p^2} \right) \right)^k \ll \exp\left( \sum_{p {\leqslant} z} \left( \frac{p}{p-1} \right)^k\frac{k}{p} \right) \\&=\exp\left\{ \sum_{p {\leqslant} z} \left( \frac{k}{p}+O\left( \frac{1}{p^2} \right) \right) \right\} \ll (\log{z})^k.\end{split}\end{align}
In a similar fashion one can show that
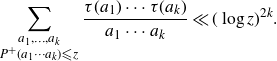 $$ \sum_{\substack{a_1,\ldots,a_k\\P^+(a_1\cdots a_k){\leqslant} z}}\frac{\tau(a_1)\cdots\tau(a_k)}{a_1\cdots a_k}\ll (\log z)^{2k}.$$
$$ \sum_{\substack{a_1,\ldots,a_k\\P^+(a_1\cdots a_k){\leqslant} z}}\frac{\tau(a_1)\cdots\tau(a_k)}{a_1\cdots a_k}\ll (\log z)^{2k}.$$
Upon recalling that
![]() $z=q^v$
for some
$z=q^v$
for some
![]() $v\gt 0$
and that
$v\gt 0$
and that
![]() $z^{30ku} = x^{{\varepsilon}}$
, the last bound, (5·37), and (5·38) imply that
$z^{30ku} = x^{{\varepsilon}}$
, the last bound, (5·37), and (5·38) imply that
5·4. The completion of the proof
Since
![]() $u={\varepsilon} V/(30kv)$
, when we put the bound (5·39) together with the definition (4·14) of S and Lemma 4·2, we infer that
$u={\varepsilon} V/(30kv)$
, when we put the bound (5·39) together with the definition (4·14) of S and Lemma 4·2, we infer that
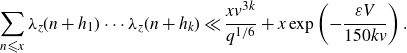 \begin{align}\sum_{n {\leqslant} x}\lambda_z(n+h_1)\cdots\lambda_z(n+h_k) \ll \frac{xv^{3k}}{q^{1/6}} + x\exp\left(-\frac{{\varepsilon} V}{150kv}\right).\end{align}
\begin{align}\sum_{n {\leqslant} x}\lambda_z(n+h_1)\cdots\lambda_z(n+h_k) \ll \frac{xv^{3k}}{q^{1/6}} + x\exp\left(-\frac{{\varepsilon} V}{150kv}\right).\end{align}
Now, if
![]() $V{\geqslant} 4\log\eta$
, then
$V{\geqslant} 4\log\eta$
, then
![]() $v=2$
, and so a combination of (5·40) with (1·1) and Lemma 4·1 yields
$v=2$
, and so a combination of (5·40) with (1·1) and Lemma 4·1 yields
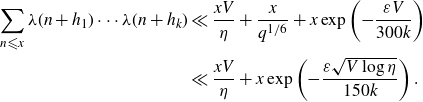 \begin{align}\begin{split}\sum_{n {\leqslant} x}\lambda(n+h_1)\cdots\lambda(n+h_k) &\ll\frac{xV}{\eta}+\frac{x}{q^{1/6}}+x\exp\left(-\frac{{\varepsilon} V}{300k}\right) \\&\ll\frac{xV}{\eta}+x\exp\left(-\frac{{\varepsilon}\sqrt{V\log\eta}}{150k}\right).\end{split}\end{align}
\begin{align}\begin{split}\sum_{n {\leqslant} x}\lambda(n+h_1)\cdots\lambda(n+h_k) &\ll\frac{xV}{\eta}+\frac{x}{q^{1/6}}+x\exp\left(-\frac{{\varepsilon} V}{300k}\right) \\&\ll\frac{xV}{\eta}+x\exp\left(-\frac{{\varepsilon}\sqrt{V\log\eta}}{150k}\right).\end{split}\end{align}
On the other hand, if
![]() $V\lt 4\log\eta$
, then
$V\lt 4\log\eta$
, then
![]() $v=\sqrt{V/(\log\eta)}\lt 2$
, so by putting the estimate (5·40) together with Lemma 4·1, it follows that
$v=\sqrt{V/(\log\eta)}\lt 2$
, so by putting the estimate (5·40) together with Lemma 4·1, it follows that
 \begin{align*}\sum_{n {\leqslant} x}\lambda(n+h_1)\cdots\lambda(n+h_k) \ll&\, \frac{x}{q^{1/6}}+x\exp\left(-\frac{{\varepsilon}\sqrt{V\log\eta}}{150k}\right)\\&+x\bigg(\frac{\log{\eta}}{V}\eta^{-\sqrt{\frac{V}{4\log{\eta}}}} +q^{-\sqrt{\frac{V}{\log\eta}}}\bigg)\bigg(V\sqrt{\frac{\log{\eta}}{V}}\bigg)^3 \\\ll&\, \frac{x}{q^{1/6}}+x\exp\left(\!-c_0\sqrt{V\log\eta}\right)\\&+x(V\log \eta)^{3/2}\exp\bigg(\!-\log{q}\sqrt{\frac{V}{\log{\eta}}} \bigg),\end{align*}
\begin{align*}\sum_{n {\leqslant} x}\lambda(n+h_1)\cdots\lambda(n+h_k) \ll&\, \frac{x}{q^{1/6}}+x\exp\left(-\frac{{\varepsilon}\sqrt{V\log\eta}}{150k}\right)\\&+x\bigg(\frac{\log{\eta}}{V}\eta^{-\sqrt{\frac{V}{4\log{\eta}}}} +q^{-\sqrt{\frac{V}{\log\eta}}}\bigg)\bigg(V\sqrt{\frac{\log{\eta}}{V}}\bigg)^3 \\\ll&\, \frac{x}{q^{1/6}}+x\exp\left(\!-c_0\sqrt{V\log\eta}\right)\\&+x(V\log \eta)^{3/2}\exp\bigg(\!-\log{q}\sqrt{\frac{V}{\log{\eta}}} \bigg),\end{align*}
where
![]() $c_0\in(0,{\varepsilon}/(150k))$
is some constant.
$c_0\in(0,{\varepsilon}/(150k))$
is some constant.
According to (1·1), we have that
![]() $xq^{-1/6}\ll x/\eta\ll xV/\eta$
and that
$xq^{-1/6}\ll x/\eta\ll xV/\eta$
and that
![]() $\log\eta\ll\log q$
. Consequently, the last bound gives
$\log\eta\ll\log q$
. Consequently, the last bound gives
where
![]() $c_1\lt c_0$
is a positive constant.
$c_1\lt c_0$
is a positive constant.
We now finish the proof of Theorem 1·2 by merging the bounds (5·41) and (5·42) from above.
Acknowledgements
We would like to thank Kaisa Matomäki for all her helpful comments and for drawing our attention to the problem addressed in this work. We also thank Cihan Sabuncu for the careful reading of an earlier version of the paper. During the making of this work, M. Jaskari was being supported by the Academy of Finland grant no. 346307 and the University of Turku Graduate School UTUGS. S. Sachpazis acknowledges support from the Academy of Finland grant no. 333707.