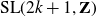1. Introduction
Thin groups are a class of groups which have a rich number of arithmetic properties that have been of interest in recent years. Given a finitely generated subgroup
![]() $\Gamma\lt\textrm{GL}(n,\mathbf{Z})$
, we let G denote its Zariski closure:
$\Gamma\lt\textrm{GL}(n,\mathbf{Z})$
, we let G denote its Zariski closure:
![]() $G\,:\!=\,\text{Zcl}(\Gamma)$
. We say that the group
$G\,:\!=\,\text{Zcl}(\Gamma)$
. We say that the group
![]() $\Gamma$
is thin if it is of infinite index in
$\Gamma$
is thin if it is of infinite index in
![]() $G(\mathbf{Z})$
(see [Reference Sarnak24]). Tools used to study these groups, such as Super Approximation, expander families and the affine sieve, have been rich areas of research that have seen a lot of progress in the last 10–15 years (see [Reference Bourgain and Gamburd4] and [Reference Bourgain, Gamburd and Sarnak5]).
$G(\mathbf{Z})$
(see [Reference Sarnak24]). Tools used to study these groups, such as Super Approximation, expander families and the affine sieve, have been rich areas of research that have seen a lot of progress in the last 10–15 years (see [Reference Bourgain and Gamburd4] and [Reference Bourgain, Gamburd and Sarnak5]).
Despite the tools available, in general it is not well understood which groups can arise as a thin subgroup of even
![]() $\textrm{SL}(n,\mathbf{R})$
. One large class of examples come from thin subgroups of
$\textrm{SL}(n,\mathbf{R})$
. One large class of examples come from thin subgroups of
![]() $\textrm{SL}(n,\mathbf{Z})$
which are isomorphic to free groups. Such subgroups are even suitably generic, providing many examples (see, for example, [Reference Fuchs and Rivin9]). Much less well understood is subgroups which are thin in
$\textrm{SL}(n,\mathbf{Z})$
which are isomorphic to free groups. Such subgroups are even suitably generic, providing many examples (see, for example, [Reference Fuchs and Rivin9]). Much less well understood is subgroups which are thin in
![]() $\textrm{SL}(n,\mathbf{R})$
but do not decompose as a free product of two proper subgroups. In this paper, we seek to further understand ways in which one might construct freely indecomposable thin subgroups of
$\textrm{SL}(n,\mathbf{R})$
but do not decompose as a free product of two proper subgroups. In this paper, we seek to further understand ways in which one might construct freely indecomposable thin subgroups of
![]() $\textrm{SL}(n,\mathbf{R})$
through methods of low-dimensional topology.
$\textrm{SL}(n,\mathbf{R})$
through methods of low-dimensional topology.
We let
![]() $S=S_g$
denote a connected, closed, orientable surface of genus
$S=S_g$
denote a connected, closed, orientable surface of genus
![]() $g\geq 2$
. Our goal will be to use techniques available to us from higher Teichmüller theory to construct discrete and faithful representations of
$g\geq 2$
. Our goal will be to use techniques available to us from higher Teichmüller theory to construct discrete and faithful representations of
![]() $\pi_1(S)$
which are Zariski dense in
$\pi_1(S)$
which are Zariski dense in
![]() $\textrm{SL}(n,\mathbf{R})$
, and contained in an arithmetic group.
$\textrm{SL}(n,\mathbf{R})$
, and contained in an arithmetic group.
The starting point of this construction is to look at points on the Hitchin component of S, which we denote by
![]() $\textrm{Hit}_n(S)$
. These are components of the
$\textrm{Hit}_n(S)$
. These are components of the
![]() $\textrm{PSL}(n,\mathbf{R})$
-character variety of S,
$\textrm{PSL}(n,\mathbf{R})$
-character variety of S,
![]() $\mathcal{R}_n(S)$
, which contain the image of Teichmüller space under the map
$\mathcal{R}_n(S)$
, which contain the image of Teichmüller space under the map
![]() $\mathcal{T}(S)\to\mathcal{R}_n(S)$
given by composing a Fuchsian representation
$\mathcal{T}(S)\to\mathcal{R}_n(S)$
given by composing a Fuchsian representation
![]() $\rho_0\,:\,\pi_1(S)\to\textrm{PSL}(2,\mathbf{R})$
with the irreducible representation
$\rho_0\,:\,\pi_1(S)\to\textrm{PSL}(2,\mathbf{R})$
with the irreducible representation
![]() $\tau_n\,:\,\textrm{PSL}(2,\mathbf{R})\to\textrm{PSL}(n,\mathbf{R})$
. These components were studied by Hitchin in [Reference Hitchin12] and later by Labourie in [Reference Labourie16] where the authors showed that the representations on these components had many of the same properties which were classical facts about representations in Teichmüller space (which we briefly summarise in Section 2). In particular, these properties of the Hitchin component ensure that the representations we construct will be discrete, faithful and can be lifted to
$\tau_n\,:\,\textrm{PSL}(2,\mathbf{R})\to\textrm{PSL}(n,\mathbf{R})$
. These components were studied by Hitchin in [Reference Hitchin12] and later by Labourie in [Reference Labourie16] where the authors showed that the representations on these components had many of the same properties which were classical facts about representations in Teichmüller space (which we briefly summarise in Section 2). In particular, these properties of the Hitchin component ensure that the representations we construct will be discrete, faithful and can be lifted to
![]() $\textrm{SL}(n,\mathbf{R})$
, thus providing a method for constructing subgroups of the form we seek.
$\textrm{SL}(n,\mathbf{R})$
, thus providing a method for constructing subgroups of the form we seek.
This method of producing Zariski dense surface subgroups of
![]() $\textrm{SL}(n,\mathbf{R})$
originates in [Reference Long and Thistlethwaite19] where the authors proved the existence of surface subgroups of
$\textrm{SL}(n,\mathbf{R})$
originates in [Reference Long and Thistlethwaite19] where the authors proved the existence of surface subgroups of
![]() $\textrm{SL}(2k+1,\mathbf{Z})$
for arbitrary
$\textrm{SL}(2k+1,\mathbf{Z})$
for arbitrary
![]() $k\geq 1$
whose image was Zariski dense in
$k\geq 1$
whose image was Zariski dense in
![]() $\textrm{SL}(2k+1,\mathbf{R})$
. The starting point for their construction is the representation coming from the hyperbolic structure on the orbifold with signature
$\textrm{SL}(2k+1,\mathbf{R})$
. The starting point for their construction is the representation coming from the hyperbolic structure on the orbifold with signature
![]() $S^2(3,4,4)$
(which is unique up to conjugacy due to these orbifolds being rigid). Direct calculation shows that the image of the representation coming from the holonomy of this hyperbolic structure can be conjugated into
$S^2(3,4,4)$
(which is unique up to conjugacy due to these orbifolds being rigid). Direct calculation shows that the image of the representation coming from the holonomy of this hyperbolic structure can be conjugated into
![]() $\textrm{SL}(n,\mathbf{Z})$
after composing with
$\textrm{SL}(n,\mathbf{Z})$
after composing with
![]() $\tau_n$
for n odd. The authors took this representation and utilised a bending construction of Thurston to deform it so that, after passing to a surface subgroup of finite index, they were left with a representation of a surface group into
$\tau_n$
for n odd. The authors took this representation and utilised a bending construction of Thurston to deform it so that, after passing to a surface subgroup of finite index, they were left with a representation of a surface group into
![]() $\textrm{SL}(2k+1,\mathbf{Z})$
with Zariski dense image. Various tools in the theory of Hitchin representations and the theory of algebraic groups were needed in their proof to ensure this bending construction could be done while preserving certain properties of the original representation, but this result provided the first examples of freely indecomposable isomorphism classes of thin subgroups of
$\textrm{SL}(2k+1,\mathbf{Z})$
with Zariski dense image. Various tools in the theory of Hitchin representations and the theory of algebraic groups were needed in their proof to ensure this bending construction could be done while preserving certain properties of the original representation, but this result provided the first examples of freely indecomposable isomorphism classes of thin subgroups of
![]() $\textrm{SL}(n,\mathbf{Z})$
for infinitely many n.
$\textrm{SL}(n,\mathbf{Z})$
for infinitely many n.
In this paper, we seek to generalise the methods used in [Reference Long and Thistlethwaite19] to show this process of bending an integral representation to being Zariski dense can also be done in a much more general context to produce more examples of Zariski dense subgroups of
![]() $\textrm{SL}(n,\mathbf{R})$
. For any subring
$\textrm{SL}(n,\mathbf{R})$
. For any subring
![]() $R\subseteq\mathbf{R}$
, we will call a representation
$R\subseteq\mathbf{R}$
, we will call a representation
![]() $\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
an R-point of the character variety if it can be conjugated in
$\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
an R-point of the character variety if it can be conjugated in
![]() $\textrm{SL}(n,\mathbf{R})$
to have image in
$\textrm{SL}(n,\mathbf{R})$
to have image in
![]() $\textrm{SL}(n,R)$
. Throughout the rest of this paper, we will let
$\textrm{SL}(n,R)$
. Throughout the rest of this paper, we will let
![]() $K/\mathbf{Q}$
be a number field with ring of integers
$K/\mathbf{Q}$
be a number field with ring of integers
![]() $\mathcal{O}_K$
. We assume that
$\mathcal{O}_K$
. We assume that
![]() $K\subset\mathbf{R}$
(so in particular, K is not totally imaginary) and that K has class number one. The class number one hypothesis is mainly for technical reasons and can perhaps be removed in future work, but our main result is the following.
$K\subset\mathbf{R}$
(so in particular, K is not totally imaginary) and that K has class number one. The class number one hypothesis is mainly for technical reasons and can perhaps be removed in future work, but our main result is the following.
Theorem 1·1. For any
![]() $n\geq 2$
, if
$n\geq 2$
, if
![]() $\textrm{Hit}_n(S)$
contains an
$\textrm{Hit}_n(S)$
contains an
![]() $\mathcal{O}_K$
point, then there is a finite sheeted cover
$\mathcal{O}_K$
point, then there is a finite sheeted cover
![]() $\widetilde{S}\to S$
so that
$\widetilde{S}\to S$
so that
![]() $\textrm{Hit}_n(\widetilde{S})$
contains an
$\textrm{Hit}_n(\widetilde{S})$
contains an
![]() $\mathcal{O}_K$
-point whose image is Zariski dense in
$\mathcal{O}_K$
-point whose image is Zariski dense in
![]() $\textrm{SL}(n,\mathbf{R})$
.
$\textrm{SL}(n,\mathbf{R})$
.
Remark 1·2. When
![]() $K\neq \mathbf{Q}$
, we prove an even stronger result (Theorem 4·4) that circumvents the need to pass to a finite sheeted cover.
$K\neq \mathbf{Q}$
, we prove an even stronger result (Theorem 4·4) that circumvents the need to pass to a finite sheeted cover.
As a consequence of Theorem 1·1, we produce many examples of groups of the form
![]() $\textrm{SL}(n,\mathcal{O}_K)$
which contain Zariski dense surface subgroups. When
$\textrm{SL}(n,\mathcal{O}_K)$
which contain Zariski dense surface subgroups. When
![]() $K\neq\mathbf{Q}$
, these groups are no longer lattices in
$K\neq\mathbf{Q}$
, these groups are no longer lattices in
![]() $\textrm{SL}(n,\mathbf{R})$
but are lattices in groups of the form
$\textrm{SL}(n,\mathbf{R})$
but are lattices in groups of the form
![]() $\textrm{SL}(n,\mathbf{R})^d$
. Therefore, Theorem 1·1 also fits into the broader framework of understanding how surface groups embed into lattices of semisimple Lie groups that has comprised much of low-dimensional topology in the last 20 years. One of the first major results in this manner is the work of [Reference Kahn and Markovic14] producing Zariski dense surface subgroups in every cocompact lattice of
$\textrm{SL}(n,\mathbf{R})^d$
. Therefore, Theorem 1·1 also fits into the broader framework of understanding how surface groups embed into lattices of semisimple Lie groups that has comprised much of low-dimensional topology in the last 20 years. One of the first major results in this manner is the work of [Reference Kahn and Markovic14] producing Zariski dense surface subgroups in every cocompact lattice of
![]() $\textrm{SL}(2,\mathbf{C})$
. Since then, similar results for the non-cocompact lattices of
$\textrm{SL}(2,\mathbf{C})$
. Since then, similar results for the non-cocompact lattices of
![]() $\textrm{SL}(2,\mathbf{C})$
(see [Reference Cooper and Futer7, Reference Kahn and Wright15]), other rank one groups (see [Reference Hamenstädt11]) and complex Lie groups (see [Reference Kahn13]) have been established. For
$\textrm{SL}(2,\mathbf{C})$
(see [Reference Cooper and Futer7, Reference Kahn and Wright15]), other rank one groups (see [Reference Hamenstädt11]) and complex Lie groups (see [Reference Kahn13]) have been established. For
![]() $\textrm{SL}(n,\mathbf{R})$
, in addition to the work of Long and Thistlethwaite for
$\textrm{SL}(n,\mathbf{R})$
, in addition to the work of Long and Thistlethwaite for
![]() $\textrm{SL}(2k+1,\mathbf{Z})$
, Audibert also used similar methods to produce Zariski dense surface subgroups of many lattices of
$\textrm{SL}(2k+1,\mathbf{Z})$
, Audibert also used similar methods to produce Zariski dense surface subgroups of many lattices of
![]() $\textrm{SL}(n,\mathbf{R})$
(see [Reference Audibert2, Reference Audibert3]). These last works, in tandem with the work of this paper, further highlight the utility of using higher Teichmüller theory to address these surface subgroup questions.
$\textrm{SL}(n,\mathbf{R})$
(see [Reference Audibert2, Reference Audibert3]). These last works, in tandem with the work of this paper, further highlight the utility of using higher Teichmüller theory to address these surface subgroup questions.
At its core, the proof of Theorem 1·1 is a construction of a similar nature to the one presented in [Reference Long and Thistlethwaite19] with some key modifications made at various steps to handle the slightly more general setup. In addition to handling the even n case, this theorem utilises a slightly different version of the bending construction more suited to the topology of S. These modifications also lend themselves to some other simplifications in the proof which we will discuss later.
When we restrict Theorem 1·1 to the case where
![]() $K=\mathbf{Q}$
, we will be left with a representation of
$K=\mathbf{Q}$
, we will be left with a representation of
![]() $\pi_1(S)$
into
$\pi_1(S)$
into
![]() $\textrm{SL}(n,\mathbf{Z})$
with Zariski dense image in
$\textrm{SL}(n,\mathbf{Z})$
with Zariski dense image in
![]() $\textrm{SL}(n,\mathbf{R})$
. The image also is of infinite index in
$\textrm{SL}(n,\mathbf{R})$
. The image also is of infinite index in
![]() $\textrm{SL}(n,\mathbf{Z})$
due to results of Margulis. Namely, since surface groups certainly surject onto
$\textrm{SL}(n,\mathbf{Z})$
due to results of Margulis. Namely, since surface groups certainly surject onto
![]() $\mathbf{Z}$
, the image will automatically be of infinite index in
$\mathbf{Z}$
, the image will automatically be of infinite index in
![]() $\textrm{SL}(n,\mathbf{Z})$
hence thin (see [Reference Margulis20]). This representation will be on the Hitchin component, hence faithful, and so the image will define a freely indecomposable thin sugroup of the form we wanted. Therefore, Theorem 1·1 leads to the following useful corollary on the existence of freely indecomposable thin subgroups of
$\textrm{SL}(n,\mathbf{Z})$
hence thin (see [Reference Margulis20]). This representation will be on the Hitchin component, hence faithful, and so the image will define a freely indecomposable thin sugroup of the form we wanted. Therefore, Theorem 1·1 leads to the following useful corollary on the existence of freely indecomposable thin subgroups of
![]() $\textrm{SL}(n,\mathbf{R})$
.
$\textrm{SL}(n,\mathbf{R})$
.
Corollary 1·3. If
![]() $\textrm{Hit}_n(S)$
contains a
$\textrm{Hit}_n(S)$
contains a
![]() $\mathbf{Z}$
point, then
$\mathbf{Z}$
point, then
![]() $\textrm{SL}(n,\mathbf{Z})$
contains a thin surface subgroup.
$\textrm{SL}(n,\mathbf{Z})$
contains a thin surface subgroup.
Thus the problem of finding non-free thin subgroups of
![]() $\textrm{SL}(n,\mathbf{R})$
can be reduced to finding integral representations of surface groups on Hitchin components. Of course, finding such representations still remains a difficult problem and at the time of writing, examples of these are only known in the case where
$\textrm{SL}(n,\mathbf{R})$
can be reduced to finding integral representations of surface groups on Hitchin components. Of course, finding such representations still remains a difficult problem and at the time of writing, examples of these are only known in the case where
![]() $n=2k+1$
is odd or
$n=2k+1$
is odd or
![]() $n=4$
.
$n=4$
.
2. Properties of Hitchin representations
The input to the construction used to prove Theorem 1·1 is a representation
![]() $\rho\,:\,\pi_1(S)\to\textrm{PSL}(n,\mathcal{O}_K)$
lying on the Hitchin component of
$\rho\,:\,\pi_1(S)\to\textrm{PSL}(n,\mathcal{O}_K)$
lying on the Hitchin component of
![]() $\mathcal{R}_n(S)$
. We start with representations on such components because they possess many useful properties akin to the representations in
$\mathcal{R}_n(S)$
. We start with representations on such components because they possess many useful properties akin to the representations in
![]() $\mathcal{T}(S)$
.
$\mathcal{T}(S)$
.
Theorem 2·1 (Labourie, [Reference Labourie16]). If
![]() $\rho\,:\,\pi_1(S)\to\textrm{PSL}(n,\mathbf{R})$
belongs to the Hitchin component, it is discrete, faithful, purely loxodromic and strongly irreducible.
$\rho\,:\,\pi_1(S)\to\textrm{PSL}(n,\mathbf{R})$
belongs to the Hitchin component, it is discrete, faithful, purely loxodromic and strongly irreducible.
In this context,
![]() $\rho$
is purely loxodromic if and only if for every non-identity element
$\rho$
is purely loxodromic if and only if for every non-identity element
![]() $\gamma\in\pi_1(S)$
,
$\gamma\in\pi_1(S)$
,
![]() $\rho(\gamma)$
is diagonalisable with real eigenvalues, all with distinct absolute values. We also say
$\rho(\gamma)$
is diagonalisable with real eigenvalues, all with distinct absolute values. We also say
![]() $\rho$
is strongly irreducible if the restriction of
$\rho$
is strongly irreducible if the restriction of
![]() $\rho$
to any finite index subgroup of
$\rho$
to any finite index subgroup of
![]() $\pi_1(S)$
is irreducible.
$\pi_1(S)$
is irreducible.
Alessandrini, Lee and Schaffhauser have also generalised the conclusions of Theorem 2·1 to also hold in the case where X is a compact, connected, hyperbolic 2-orbifold with nonempty singular locus, and possibly with boundary. Their result ([Reference Alessandrini, Lee and Schaffhauser1, theorem 2·28]) provides many of the same properties for non-closed surfaces which will be necessary for the bending construction of Section 3.
The main utility of this theorem is that the bending process we use to deform
![]() $\rho$
preserves the path component
$\rho$
preserves the path component
![]() $\rho$
lies on in
$\rho$
lies on in
![]() $\mathcal{R}_n(S)$
. Thus as
$\mathcal{R}_n(S)$
. Thus as
![]() $\rho$
originally lied on the Hitchin component, then so will the bent representation, hence it will still be discrete, faithful and purely loxodromic.
$\rho$
originally lied on the Hitchin component, then so will the bent representation, hence it will still be discrete, faithful and purely loxodromic.
We may also circumvent the (mild) annoyance of having to work with projective matrices due to the fact that representations in
![]() $\mathcal{T}(S)$
can be lifted to
$\mathcal{T}(S)$
can be lifted to
![]() $\textrm{SL}(2,\mathbf{R})$
and the fact that the Hitchin component is connected. Namely, we have the following (Reference Culler8, theorem 4·1).
$\textrm{SL}(2,\mathbf{R})$
and the fact that the Hitchin component is connected. Namely, we have the following (Reference Culler8, theorem 4·1).
Lemma 2·2. Let
![]() $\rho\,:\,\pi_1(S)\to\textrm{PSL}(n,\mathbf{R})$
be a representation on the Hitchin component. Then
$\rho\,:\,\pi_1(S)\to\textrm{PSL}(n,\mathbf{R})$
be a representation on the Hitchin component. Then
![]() $\rho$
admits a lift
$\rho$
admits a lift
![]() $\widetilde{\rho}\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
. Moreover, for any nontrivial
$\widetilde{\rho}\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
. Moreover, for any nontrivial
![]() $\gamma\in\pi_1(S)$
, the lift
$\gamma\in\pi_1(S)$
, the lift
![]() $\widetilde{\rho}$
can be chosen so that
$\widetilde{\rho}$
can be chosen so that
![]() $\widetilde{\rho}(\gamma)$
has distinct positive real eigenvalues.
$\widetilde{\rho}(\gamma)$
has distinct positive real eigenvalues.
For the rest of this paper, we will assume our starting representation on the Hitchin component takes the form
![]() $\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathcal{O}_K)$
. For convenience as well, whenever we fix a nontrivial
$\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathcal{O}_K)$
. For convenience as well, whenever we fix a nontrivial
![]() $\gamma\in\pi_1(S)$
, we will assume we have chosen the lift of the representation so that
$\gamma\in\pi_1(S)$
, we will assume we have chosen the lift of the representation so that
![]() $\rho(\gamma)$
then also has distinct, positive real eigenvalues. Aside from just notational convenience, these lifted representations will still be discrete and faithful due to being on the Hitchin component and so their images will define non-free subgroups of
$\rho(\gamma)$
then also has distinct, positive real eigenvalues. Aside from just notational convenience, these lifted representations will still be discrete and faithful due to being on the Hitchin component and so their images will define non-free subgroups of
![]() $\textrm{SL}(n,\mathcal{O}_K)$
of the form we wish to study.
$\textrm{SL}(n,\mathcal{O}_K)$
of the form we wish to study.
From this point, the goal will be to take the representation
![]() $\rho$
and perform a series of deformations so that, after possibly passing to a finite sheeted cover, we are left with a representation of a surface group into
$\rho$
and perform a series of deformations so that, after possibly passing to a finite sheeted cover, we are left with a representation of a surface group into
![]() $\textrm{SL}(n,\mathcal{O}_K)$
which is Zariski dense in
$\textrm{SL}(n,\mathcal{O}_K)$
which is Zariski dense in
![]() $\textrm{SL}(n,\mathbf{R})$
. The following theorem will be crucial to establishing this result.
$\textrm{SL}(n,\mathbf{R})$
. The following theorem will be crucial to establishing this result.
Theorem 2·3 (Guichard, [Reference Guichard10]). Let
![]() $\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
be a lift of a representation on the Hitchin component and let G be the Zariski closure of
$\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
be a lift of a representation on the Hitchin component and let G be the Zariski closure of
![]() $\rho(\pi_1(S))$
. Then G is conjugate to one of the following groups:
$\rho(\pi_1(S))$
. Then G is conjugate to one of the following groups:
-
(i)
 $\tau_n(\textrm{SL}(2,\mathbf{R}))$
;
$\tau_n(\textrm{SL}(2,\mathbf{R}))$
; -
(ii)
 $\textrm{Sp}(2k,\mathbf{R})$
if
$\textrm{Sp}(2k,\mathbf{R})$
if
 $n=2k$
is even;
$n=2k$
is even; -
(iii)
 $\textrm{SO}(k+1,k)$
if
$\textrm{SO}(k+1,k)$
if
 $n=2k+1$
is odd;
$n=2k+1$
is odd; -
(iv) the image of the 7-dimensional fundamental representation of the short root of
 $G_2$
;
$G_2$
; -
(v)
 $\textrm{SL}(n,\mathbf{R})$
.
$\textrm{SL}(n,\mathbf{R})$
.
Remark 2·4. An alternate proof of this same classification is also given in [Reference Sambarino23].
We will assume
![]() $n\neq 7$
for simplicity so that the possible Zariski closures will only be conjugate to options (i)–(iii) or (v) in the above list. From here, we will show that if the Zariski closure of
$n\neq 7$
for simplicity so that the possible Zariski closures will only be conjugate to options (i)–(iii) or (v) in the above list. From here, we will show that if the Zariski closure of
![]() $\rho(\pi_1(S))$
is one of (i)–(iii) in the above list, then there is a deformation of
$\rho(\pi_1(S))$
is one of (i)–(iii) in the above list, then there is a deformation of
![]() $\rho$
with the properties that it is: K-integral, on the Hitchin component and has a strictly larger Zariski closure. By performing this deformation multiple times if necessary, we will be able to guarantee that the Zariski closure at the final stage will be all of
$\rho$
with the properties that it is: K-integral, on the Hitchin component and has a strictly larger Zariski closure. By performing this deformation multiple times if necessary, we will be able to guarantee that the Zariski closure at the final stage will be all of
![]() $\textrm{SL}(n,\mathbf{R})$
hence define a Zariski dense subgroup. Guichard’s classification of possible Zariski closures is also used in this manner in [Reference Long and Thistlethwaite19], but also relies on a generalisation of the result to representations of orbifold fundamental groups on Hitchin components found in [Reference Alessandrini, Lee and Schaffhauser1].
$\textrm{SL}(n,\mathbf{R})$
hence define a Zariski dense subgroup. Guichard’s classification of possible Zariski closures is also used in this manner in [Reference Long and Thistlethwaite19], but also relies on a generalisation of the result to representations of orbifold fundamental groups on Hitchin components found in [Reference Alessandrini, Lee and Schaffhauser1].
3. Bending around nonseparating curves
We now describe the bending construction which will be used to deform the representations in order to successively enlarge the Zariski closures of the image. For our surface
![]() $S=S_g$
, we fix a nonseparating simple closed curve
$S=S_g$
, we fix a nonseparating simple closed curve
![]() $\gamma$
. We let S
′ denote the compact surface one gets by cutting S along
$\gamma$
. We let S
′ denote the compact surface one gets by cutting S along
![]() $\gamma$
and denote by
$\gamma$
and denote by
![]() $\gamma_1$
and
$\gamma_1$
and
![]() $\gamma_2$
the two boundary components of S ′. Up to some homeomorphism of S, we can suppose our setup is of the form in Figure 1.
$\gamma_2$
the two boundary components of S ′. Up to some homeomorphism of S, we can suppose our setup is of the form in Figure 1.

Fig. 1. The setup for the bending construction.
In S, the curves
![]() $\gamma$
,
$\gamma$
,
![]() $\gamma_1$
and
$\gamma_1$
and
![]() $\gamma_2$
will all be freely homotopic, and by an abuse of notation, we will write
$\gamma_2$
will all be freely homotopic, and by an abuse of notation, we will write
![]() $\gamma_1$
and
$\gamma_1$
and
![]() $\gamma_2$
to denote the elements of
$\gamma_2$
to denote the elements of
![]() $\pi_1(S')$
and identify
$\pi_1(S')$
and identify
![]() $\gamma$
with
$\gamma$
with
![]() $\gamma_1$
in
$\gamma_1$
in
![]() $\pi_1(S)$
. In this setup, it is known that
$\pi_1(S)$
. In this setup, it is known that
![]() $\pi_1(S)$
can be written as the following HNN extension:
$\pi_1(S)$
can be written as the following HNN extension:
Given any representation
![]() $\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
and any matrix
$\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
and any matrix
![]() $A\in\textrm{SL}(n,\mathbf{R})$
in the centraliser of
$A\in\textrm{SL}(n,\mathbf{R})$
in the centraliser of
![]() $\rho(\gamma)$
, we can define a new bent representation
$\rho(\gamma)$
, we can define a new bent representation
![]() $\rho^A\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
by setting:
$\rho^A\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
by setting:
With extra care for the choice of centralizing A, this bending procedure will also preserve a number of useful properties of the original representation.
Firstly, if
![]() $\rho$
has image in
$\rho$
has image in
![]() $\textrm{SL}(n,\mathcal{O}_K)$
and we choose A in the
$\textrm{SL}(n,\mathcal{O}_K)$
and we choose A in the
![]() $\mathcal{O}_K$
-centralizer of
$\mathcal{O}_K$
-centralizer of
![]() $\rho(\gamma)$
, then it’s clear from the formula of the bend that
$\rho(\gamma)$
, then it’s clear from the formula of the bend that
![]() $\rho^A$
still has image inside of
$\rho^A$
still has image inside of
![]() $\textrm{SL}(n,\mathcal{O}_K)$
. So with additional care, the bending construction can be done in such a way as to preserve K-integrality of the original representation.
$\textrm{SL}(n,\mathcal{O}_K)$
. So with additional care, the bending construction can be done in such a way as to preserve K-integrality of the original representation.
Secondly, if we take care to choose A so that
![]() $A=\exp(X)$
for some diagonalizable
$A=\exp(X)$
for some diagonalizable
![]() $X\in\mathfrak{sl}(n,\mathbf{R})$
, then there is a one-parameter family of matrices given by
$X\in\mathfrak{sl}(n,\mathbf{R})$
, then there is a one-parameter family of matrices given by
for
![]() $t\in\mathbf{R}$
. For this one-parameter family, we have that
$t\in\mathbf{R}$
. For this one-parameter family, we have that
![]() $A_0=I_n$
,
$A_0=I_n$
,
![]() $A_1=A$
. Moreover, by diagonalisability, for any
$A_1=A$
. Moreover, by diagonalisability, for any
![]() $t\in\mathbf{R}$
$t\in\mathbf{R}$
![]() $A_t$
still centralises
$A_t$
still centralises
![]() $\rho(\gamma)$
. Note that we are using the fact that
$\rho(\gamma)$
. Note that we are using the fact that
![]() $\rho(\gamma)$
is also diagonalisable as
$\rho(\gamma)$
is also diagonalisable as
![]() $\rho$
lies on the Hitchin component to guarantee the matrices
$\rho$
lies on the Hitchin component to guarantee the matrices
![]() $A_t$
all still centralise
$A_t$
all still centralise
![]() $\rho(\gamma)$
. But in particular, this one-parameter family of matrices
$\rho(\gamma)$
. But in particular, this one-parameter family of matrices
![]() $A_t$
defines a path of representations
$A_t$
defines a path of representations
![]() $\rho^{A_t}\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
from
$\rho^{A_t}\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{R})$
from
![]() $\rho^{A_0}=\rho$
to
$\rho^{A_0}=\rho$
to
![]() $\rho^{A_1}=\rho^A$
. Thus,
$\rho^{A_1}=\rho^A$
. Thus,
![]() $\rho^A$
lies on the same path component of
$\rho^A$
lies on the same path component of
![]() $\mathcal{R}_n(S)$
as
$\mathcal{R}_n(S)$
as
![]() $\rho$
. In particular, as
$\rho$
. In particular, as
![]() $\rho$
is a Hitchin representation, so is
$\rho$
is a Hitchin representation, so is
![]() $\rho^A$
.
$\rho^A$
.
So in short, many of the desired properties of the original representation can be preserved by careful choice of the bending matrix A, used to deform
![]() $\rho$
. However, bending construction in this context is useful not just for its ability to preserve “nice” properties of our representations, but to “improve” them in the sense of producing representations with larger Zariski closures. What ultimately enables this is the following.
$\rho$
. However, bending construction in this context is useful not just for its ability to preserve “nice” properties of our representations, but to “improve” them in the sense of producing representations with larger Zariski closures. What ultimately enables this is the following.
Lemma 3·1. Suppose
![]() $\rho(\pi_1(S))$
has Zariski closure contained in
$\rho(\pi_1(S))$
has Zariski closure contained in
![]() $G\neq\textrm{SL}(n,\mathbf{R})$
. If in addition to the above properties, we choose
$G\neq\textrm{SL}(n,\mathbf{R})$
. If in addition to the above properties, we choose
![]() $A\notin G$
, then the Zariski closure of
$A\notin G$
, then the Zariski closure of
![]() $\rho^A(\pi_1(S))$
is strictly larger than G.
$\rho^A(\pi_1(S))$
is strictly larger than G.
Proof. The Zariski closure of
![]() $\rho^A(\pi_1(S))$
must still be among the ones of Theorem 2·3 as
$\rho^A(\pi_1(S))$
must still be among the ones of Theorem 2·3 as
![]() $\rho^A$
is still on the Hitchin component of S. A priori, it may be unclear why the image of
$\rho^A$
is still on the Hitchin component of S. A priori, it may be unclear why the image of
![]() $\rho^A$
might not be some nontrivial conjugate of G or a proper subgroup of it, but we can rule each of these possibilities out as well, thus guaranteeing that the Zariski closure must indeed get larger.
$\rho^A$
might not be some nontrivial conjugate of G or a proper subgroup of it, but we can rule each of these possibilities out as well, thus guaranteeing that the Zariski closure must indeed get larger.
As
![]() $G\neq\textrm{SL}(n,\mathbf{R})$
, consulting the list of Theorem 2·3, we see that either G is conjugate to either
$G\neq\textrm{SL}(n,\mathbf{R})$
, consulting the list of Theorem 2·3, we see that either G is conjugate to either
![]() $\tau_n(\textrm{SL}(2,\mathbf{R}))$
,
$\tau_n(\textrm{SL}(2,\mathbf{R}))$
,
![]() $\textrm{Sp}(2k,\mathbf{R})$
or
$\textrm{Sp}(2k,\mathbf{R})$
or
![]() $\textrm{SO}(k+1,k)$
. In the first case,
$\textrm{SO}(k+1,k)$
. In the first case,
![]() $\rho^A(\pi_1(S))$
can’t have a smaller Zariski closure as no proper subgroup of
$\rho^A(\pi_1(S))$
can’t have a smaller Zariski closure as no proper subgroup of
![]() $\tau_n(\textrm{SL}(2,\mathbf{R}))$
is a possible Zariski closure for a Hitchin representation. In the latter two cases, it follows that there is some alternating or symmetric bilinear form, J, which is preserved by the image of
$\tau_n(\textrm{SL}(2,\mathbf{R}))$
is a possible Zariski closure for a Hitchin representation. In the latter two cases, it follows that there is some alternating or symmetric bilinear form, J, which is preserved by the image of
![]() $\rho$
. Basic calculations verify that the image of
$\rho$
. Basic calculations verify that the image of
![]() $\textrm{SL}(2,\mathbf{R})$
under the irreducible representation
$\textrm{SL}(2,\mathbf{R})$
under the irreducible representation
![]() $\tau_n$
is contained in
$\tau_n$
is contained in
![]() $\textrm{Sp}(2k,\mathbf{R})$
in the n even case and
$\textrm{Sp}(2k,\mathbf{R})$
in the n even case and
![]() $\textrm{SO}(k+1,k)$
in the n odd case. Therefore, if
$\textrm{SO}(k+1,k)$
in the n odd case. Therefore, if
![]() $\rho^A(\pi_1(S))$
had Zariski closure smaller than G, then the it must be
$\rho^A(\pi_1(S))$
had Zariski closure smaller than G, then the it must be
![]() $\tau_n(\textrm{SL}(2,\mathbf{R}))$
in which case, the same form J is still preserved. But this cannot be as A won’t preserve J by virtue of not being in G.
$\tau_n(\textrm{SL}(2,\mathbf{R}))$
in which case, the same form J is still preserved. But this cannot be as A won’t preserve J by virtue of not being in G.
All that remains is to rule out why the Zariski closure of
![]() $\rho^A(\pi_1(S))$
can’t be some nontrivial conjugate of G. If this were the case, then there would be another non-degenerate (symmetric or alternating) bilinear form J ′ which is preserved by the image of
$\rho^A(\pi_1(S))$
can’t be some nontrivial conjugate of G. If this were the case, then there would be another non-degenerate (symmetric or alternating) bilinear form J ′ which is preserved by the image of
![]() $\rho^A(\pi_1(S))$
. But now, observe that the representations
$\rho^A(\pi_1(S))$
. But now, observe that the representations
![]() $\rho$
and
$\rho$
and
![]() $\rho^A$
are identical on the compact subsurface
$\rho^A$
are identical on the compact subsurface
![]() $S'\subset S$
. In particular, the image of the representation
$S'\subset S$
. In particular, the image of the representation
![]() $\rho|_{\pi_1(S')}=\rho^A|_{\pi_1(S')}$
preserves both the forms J and J
′.
$\rho|_{\pi_1(S')}=\rho^A|_{\pi_1(S')}$
preserves both the forms J and J
′.
As both J and J’ are preserved,
![]() $J^{-1}J'\rho(\beta)=\rho(\beta)J^{-1}J'$
for all
$J^{-1}J'\rho(\beta)=\rho(\beta)J^{-1}J'$
for all
![]() $\beta\in\pi_1(S')$
. The subgroup
$\beta\in\pi_1(S')$
. The subgroup
![]() $\pi_1(S')$
has Zariski closure at least containing an (absolutely irreducible) principal
$\pi_1(S')$
has Zariski closure at least containing an (absolutely irreducible) principal
![]() $\textrm{SL}(2,\mathbf{R})$
.
$\textrm{SL}(2,\mathbf{R})$
.
![]() $J^{-1}J'$
centralises all of this principal
$J^{-1}J'$
centralises all of this principal
![]() $\textrm{SL}(2,\mathbf{R})$
, hence by Schur’s lemma, is a homothety. In particular, J and J’ are scalar multiples of one another and define the same orthogonal or symplectic groups.
$\textrm{SL}(2,\mathbf{R})$
, hence by Schur’s lemma, is a homothety. In particular, J and J’ are scalar multiples of one another and define the same orthogonal or symplectic groups.
Thus the Zariski closure of
![]() $\rho^A(\pi_1(S))$
cannot be a subgroup of, or a conjugate of G, and thus must be strictly larger among the possibilities provided by Guichard’s list.
$\rho^A(\pi_1(S))$
cannot be a subgroup of, or a conjugate of G, and thus must be strictly larger among the possibilities provided by Guichard’s list.
This lemma also highlights why we restrict to bends about nonseparating simple closed curves. Given a separating simple closed curve, similar bending deformations can be defined via a splitting of
![]() $\pi_1(S)$
as an amalgamated free product of the fundamental groups of each component of the cut surface. However, in order to produce representations with strictly larger Zariski closure by bending about a separating curve, one would instead need to choose bending matrices A which lie outside the normaliser of the Zariski closure of the original representation. This condition is more restrictive, hence the construction is easier in the nonseparating case.
$\pi_1(S)$
as an amalgamated free product of the fundamental groups of each component of the cut surface. However, in order to produce representations with strictly larger Zariski closure by bending about a separating curve, one would instead need to choose bending matrices A which lie outside the normaliser of the Zariski closure of the original representation. This condition is more restrictive, hence the construction is easier in the nonseparating case.
Theorem 1·1 is then proven by repeated applications of the bending constructions as follows.
Proof of
1·1. We let
![]() $\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathcal{O}_K)$
be a representation on the Hitchin component with Zariski closure
$\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathcal{O}_K)$
be a representation on the Hitchin component with Zariski closure
![]() $G\neq\textrm{SL}(n,\mathbf{R})$
. By the various methods in Section 4 we can construct a matrix
$G\neq\textrm{SL}(n,\mathbf{R})$
. By the various methods in Section 4 we can construct a matrix
![]() $A\in\textrm{SL}(n,\mathcal{O}_K)$
satisfying the following properties:
$A\in\textrm{SL}(n,\mathcal{O}_K)$
satisfying the following properties:
-
(a) A centralises
 $\rho(\gamma)$
for some nonseparating simple closed curve
$\rho(\gamma)$
for some nonseparating simple closed curve
 $\gamma$
(after possibly passing to a finite sheeted cover
$\gamma$
(after possibly passing to a finite sheeted cover
 $\widetilde{S}\to S$
);
$\widetilde{S}\to S$
); -
(b)
 $A\notin G$
;
$A\notin G$
; -
(c)
 $A=\exp(X)$
for some diagonalisable
$A=\exp(X)$
for some diagonalisable
 $X\in\mathfrak{sl}(n,\mathbf{R})$
.
$X\in\mathfrak{sl}(n,\mathbf{R})$
.
From such a matrix, property (a) allows us to form the new bent representation
![]() $\rho^A$
. By property (b), along with Lemma 3·1, this also guarantees that
$\rho^A$
. By property (b), along with Lemma 3·1, this also guarantees that
![]() $\rho^A(\pi_1(\widetilde{S}))$
has a larger Zariski closure than G.
$\rho^A(\pi_1(\widetilde{S}))$
has a larger Zariski closure than G.
![]() $\rho^A$
still remains on the Hitchin component of
$\rho^A$
still remains on the Hitchin component of
![]() $\widetilde{S}$
by property (c) as outlined at the beginning of this section.
$\widetilde{S}$
by property (c) as outlined at the beginning of this section.
We can then repeat this process (at most twice, when
![]() $n\neq 7$
) until all of the finitely many possible Zariski closures of Theorem 2·3 are ruled out except for
$n\neq 7$
) until all of the finitely many possible Zariski closures of Theorem 2·3 are ruled out except for
![]() $\textrm{SL}(n,\mathbf{R})$
itself at which point, the final representation must be Zariski dense, K-integral and on the Hitchin component.
$\textrm{SL}(n,\mathbf{R})$
itself at which point, the final representation must be Zariski dense, K-integral and on the Hitchin component.
4. Constructing the bending matrices
To complete the proof of Theorem 1·1, it remains to be shown how one may construct the matrices A satisfying each of properties (a)–(c) used in the proof. Different techniques for constructing such a matrix are needed depending on the various possibilities of the initial Zariski closure provided by Theorem 2·3 as well as the properties of the number field K. Before we discuss the specific methods used to construct A in each case, we record the following pair of useful lemmas here which will be used throughout.
Lemma 4·1. Given
![]() $M\in\textrm{SL}(n,K)$
whose characteristic polynomial is in
$M\in\textrm{SL}(n,K)$
whose characteristic polynomial is in
![]() $\mathcal{O}_K[t]$
, then there is some
$\mathcal{O}_K[t]$
, then there is some
![]() $j\gt0$
so that
$j\gt0$
so that
![]() $M^j\in\textrm{SL}(n,\mathcal{O}_K)$
.
$M^j\in\textrm{SL}(n,\mathcal{O}_K)$
.
Proof. Using the rational canonical form of M, there is a
![]() $P\in\textrm{GL}(n,K)$
so that
$P\in\textrm{GL}(n,K)$
so that
![]() $M=PRP^{-1}$
where
$M=PRP^{-1}$
where
![]() $R\in\textrm{SL}(n,\mathcal{O}_K)$
. Already here, we are implicitly using the hypothesis that K have class number one to guarantee that
$R\in\textrm{SL}(n,\mathcal{O}_K)$
. Already here, we are implicitly using the hypothesis that K have class number one to guarantee that
![]() $R\in\textrm{SL}(n,\mathcal{O}_K)$
. Namely, if
$R\in\textrm{SL}(n,\mathcal{O}_K)$
. Namely, if
![]() $f\in\mathcal{O}_K[t]$
denotes the characteristic polynomial of M, then a factorization of f into irreducibles over
$f\in\mathcal{O}_K[t]$
denotes the characteristic polynomial of M, then a factorization of f into irreducibles over
![]() $\mathcal{O}_K$
will be a factorisation into irreducibles over K by Gauss’s lemma as
$\mathcal{O}_K$
will be a factorisation into irreducibles over K by Gauss’s lemma as
![]() $\mathcal{O}_K$
is a UFD. Thus the invariant factors of f can be guaranteed to all be in
$\mathcal{O}_K$
is a UFD. Thus the invariant factors of f can be guaranteed to all be in
![]() $\mathcal{O}_K[t]$
as well and so the rational canonical form of f will have entries in
$\mathcal{O}_K[t]$
as well and so the rational canonical form of f will have entries in
![]() $\mathcal{O}_K$
.
$\mathcal{O}_K$
.
For any
![]() $N\in\mathcal{O}_K$
, we consider the reduction map
$N\in\mathcal{O}_K$
, we consider the reduction map
![]() $\textrm{SL}(n,\mathcal{O}_K)\to\textrm{SL}(n,\mathcal{O}_K/(N))$
.
$\textrm{SL}(n,\mathcal{O}_K)\to\textrm{SL}(n,\mathcal{O}_K/(N))$
.
![]() $\textrm{SL}(n,\mathcal{O}_K/(N))$
is finite so there is some j so that
$\textrm{SL}(n,\mathcal{O}_K/(N))$
is finite so there is some j so that
![]() $R^j\equiv I\pmod{(N)}$
. In other words,
$R^j\equiv I\pmod{(N)}$
. In other words,
![]() $R^j=I+NX$
for some
$R^j=I+NX$
for some
![]() $X\in\text{M}_n(\mathcal{O}_K)$
. In this case, we have that
$X\in\text{M}_n(\mathcal{O}_K)$
. In this case, we have that
In the above expression, the only term depending on N (other than N itself) is X, which already has integral entries. Thus, if we pick
![]() $N\in\mathcal{O}_K$
so that it clears all the denominators of all entries in P and
$N\in\mathcal{O}_K$
so that it clears all the denominators of all entries in P and
![]() $P^{-1}$
, we get that
$P^{-1}$
, we get that
![]() $M^j\in\textrm{SL}(n,\mathcal{O}_K)$
.
$M^j\in\textrm{SL}(n,\mathcal{O}_K)$
.
Lemma 4·2. Suppose
![]() $\rho(\gamma)\in\textrm{SL}(n,\mathcal{O}_K)$
has characteristic polynomial f(t) where
$\rho(\gamma)\in\textrm{SL}(n,\mathcal{O}_K)$
has characteristic polynomial f(t) where
![]() $f\in\mathcal{O}_K[t]$
is irreducible over
$f\in\mathcal{O}_K[t]$
is irreducible over
![]() $\mathcal{O}_K$
. Then there is some
$\mathcal{O}_K$
. Then there is some
![]() $A\in\textrm{SL}(n,\mathcal{O}_K)$
centralizing
$A\in\textrm{SL}(n,\mathcal{O}_K)$
centralizing
![]() $\rho(\gamma)$
, not preserving the form J and so that
$\rho(\gamma)$
, not preserving the form J and so that
![]() $A=\exp(X)$
for some diagonalisable
$A=\exp(X)$
for some diagonalisable
![]() $X\in\mathfrak{sl}(n,\mathbf{R})$
.
$X\in\mathfrak{sl}(n,\mathbf{R})$
.
Proof. As f is irreducible over the UFD
![]() $\mathcal{O}_K$
, it is irreducible over K. Let
$\mathcal{O}_K$
, it is irreducible over K. Let
![]() $\alpha\in\overline{K}$
denote some root of f and consider the extension
$\alpha\in\overline{K}$
denote some root of f and consider the extension
![]() $K(\alpha)/K$
. Note that
$K(\alpha)/K$
. Note that
![]() $[K(\alpha)\,:\,K]=n$
as f must be the minimal polynomial of
$[K(\alpha)\,:\,K]=n$
as f must be the minimal polynomial of
![]() $\alpha$
. All the roots of f must be distinct and real as
$\alpha$
. All the roots of f must be distinct and real as
![]() $\rho$
is on the Hitchin component (2.1) and so
$\rho$
is on the Hitchin component (2.1) and so
![]() $K(\alpha)$
has at least n real embeddings as we may extend the (fixed) real embedding of K to one of
$K(\alpha)$
has at least n real embeddings as we may extend the (fixed) real embedding of K to one of
![]() $K(\alpha)$
by sending
$K(\alpha)$
by sending
![]() $\alpha$
to any of the other real roots of f. As a consequence, the unit group
$\alpha$
to any of the other real roots of f. As a consequence, the unit group
![]() $\mathcal{O}_{K(\alpha)}^\times$
has rank
$\mathcal{O}_{K(\alpha)}^\times$
has rank
![]() $\geq n-1$
.
$\geq n-1$
.
By diagonalising
![]() $\rho(\gamma)$
over
$\rho(\gamma)$
over
![]() $\mathbf{R}$
and using the fact that it has distinct real eigenvalues, one sees that the centralizer of
$\mathbf{R}$
and using the fact that it has distinct real eigenvalues, one sees that the centralizer of
![]() $\rho(\gamma)$
in
$\rho(\gamma)$
in
![]() $\textrm{SO}(J;\,\mathbf{R})$
has rank
$\textrm{SO}(J;\,\mathbf{R})$
has rank
![]() $\frac{n}{2}$
. In comparison,
$\frac{n}{2}$
. In comparison,
![]() $\mathcal{O}_{K(\alpha)}^\times$
has rank
$\mathcal{O}_{K(\alpha)}^\times$
has rank
![]() $\geq n-1$
. Then
$\geq n-1$
. Then
![]() $n-1\gt {n}/{2}$
as long as
$n-1\gt {n}/{2}$
as long as
![]() $n\gt2$
.
$n\gt2$
.
Note then that there is a K-algebra isomorphism
sending
![]() $\alpha\mapsto\rho(\gamma)$
because both of the above algebras are isomorphic to
$\alpha\mapsto\rho(\gamma)$
because both of the above algebras are isomorphic to
![]() $K[t]/(f)$
for the monic irreducible
$K[t]/(f)$
for the monic irreducible
![]() $f\in\mathcal{O}_K[t]$
. Consider now, the image of
$f\in\mathcal{O}_K[t]$
. Consider now, the image of
![]() $\mathcal{O}_{K(\alpha)}^\times$
in
$\mathcal{O}_{K(\alpha)}^\times$
in
![]() $K[\rho(\gamma)]$
. By the above rank considerations, there is some infinite order
$K[\rho(\gamma)]$
. By the above rank considerations, there is some infinite order
![]() $u\in\mathcal{O}_{K(\alpha)}^\times$
whose image,
$u\in\mathcal{O}_{K(\alpha)}^\times$
whose image,
![]() $A'\in K[\rho(\gamma)]$
, satisfies the property that no power of A
′ preserves the form J. Further assume that
$A'\in K[\rho(\gamma)]$
, satisfies the property that no power of A
′ preserves the form J. Further assume that
![]() $u\gt0$
by replacing u with
$u\gt0$
by replacing u with
![]() $-u$
if necessary. A
′ is a polynomial in powers of
$-u$
if necessary. A
′ is a polynomial in powers of
![]() $\rho(\gamma)$
and so A’ itself will still centralise
$\rho(\gamma)$
and so A’ itself will still centralise
![]() $\rho(\gamma)$
.
$\rho(\gamma)$
.
At the moment, A’ still has some possibly undesirable properties, but we will modify it to construct the matrix A. First, note A’ has characteristic polynomial in
![]() $\mathcal{O}_K[t]$
: its characteristic polynomial factors as
$\mathcal{O}_K[t]$
: its characteristic polynomial factors as
![]() $\prod_{i=1}^n(t-u^{\sigma_i})$
where the
$\prod_{i=1}^n(t-u^{\sigma_i})$
where the
![]() $\sigma_i\,:\,K(\alpha)\to\mathbf{C}$
are the K-embeddings of
$\sigma_i\,:\,K(\alpha)\to\mathbf{C}$
are the K-embeddings of
![]() $K(\alpha)$
. The determinant of A’ at the moment is
$K(\alpha)$
. The determinant of A’ at the moment is
![]() $v=\text{Norm}_{K(\alpha)/K}(u)\in\mathcal{O}_K^\times$
, but we may pass to a higher power of A’ and rescale by some power of
$v=\text{Norm}_{K(\alpha)/K}(u)\in\mathcal{O}_K^\times$
, but we may pass to a higher power of A’ and rescale by some power of
![]() $v^{-1}$
so that A’ has determinant 1. This power of A’ then has characteristic polynomial in
$v^{-1}$
so that A’ has determinant 1. This power of A’ then has characteristic polynomial in
![]() $\mathcal{O}_K[t]$
and is in
$\mathcal{O}_K[t]$
and is in
![]() $\textrm{SL}(n,K)$
, hence by Lemma 4·1, some further suitable power will have entries in
$\textrm{SL}(n,K)$
, hence by Lemma 4·1, some further suitable power will have entries in
![]() $\mathcal{O}_K$
. Taking
$\mathcal{O}_K$
. Taking
![]() $A=(A')^j$
to be such a large enough power, we get
$A=(A')^j$
to be such a large enough power, we get
![]() $A\in\textrm{SL}(n,\mathcal{O}_K)$
.
$A\in\textrm{SL}(n,\mathcal{O}_K)$
.
This matrix
![]() $A=(A')^j\in\textrm{SL}(n,\mathcal{O}_K)$
still centralises
$A=(A')^j\in\textrm{SL}(n,\mathcal{O}_K)$
still centralises
![]() $\rho(\gamma)$
and does not preserve the form J as no power of A’ preserves J by construction. Furthermore, such an A will be the exponential of some diagonalisable matrix as we arranged for
$\rho(\gamma)$
and does not preserve the form J as no power of A’ preserves J by construction. Furthermore, such an A will be the exponential of some diagonalisable matrix as we arranged for
![]() $u\gt0$
and as A’ is a polynomial in powers of
$u\gt0$
and as A’ is a polynomial in powers of
![]() $\rho(\gamma)$
, all of which are the exponential of some diagonal matrix by Theorem 2·1.
$\rho(\gamma)$
, all of which are the exponential of some diagonal matrix by Theorem 2·1.
Remark 4·3. In the odd-dimensional case, for non-Zariski dense
![]() $\rho$
, the characteristic polynomials of the
$\rho$
, the characteristic polynomials of the
![]() $\rho(\gamma)$
are never irreducible over
$\rho(\gamma)$
are never irreducible over
![]() $\mathcal{O}_K$
as they always have an eigenvalue of 1, due to being on the Hitchin component. Nonetheless, the same conclusion of this lemma can easily be adopted to the odd-dimensional case if we find
$\mathcal{O}_K$
as they always have an eigenvalue of 1, due to being on the Hitchin component. Nonetheless, the same conclusion of this lemma can easily be adopted to the odd-dimensional case if we find
![]() $\rho(\gamma)$
with characteristic polynomial of the form
$\rho(\gamma)$
with characteristic polynomial of the form
![]() $(t-1)f(t)$
for some
$(t-1)f(t)$
for some
![]() $f(t)\in\mathcal{O}_K[t]$
irreducible over
$f(t)\in\mathcal{O}_K[t]$
irreducible over
![]() $\mathcal{O}_K$
since we may conjugate
$\mathcal{O}_K$
since we may conjugate
![]() $\rho(\gamma)$
to be in block diagonal form with an
$\rho(\gamma)$
to be in block diagonal form with an
![]() $(n-1)\times(n-1)$
-block along the diagonal. In this case, applying this result to this block gives the bending matrix A in the odd-dimensional case.
$(n-1)\times(n-1)$
-block along the diagonal. In this case, applying this result to this block gives the bending matrix A in the odd-dimensional case.
This lemma provides sufficient conditions for which the bending matrix A used in the proof of Theorem 1·1 will exist. This implies that to construct a bending matrix, it suffices to find a nonseparating simple closed curve
![]() $\gamma\in\pi_1(S)$
whose characteristic polynomials are of the form f(t) or
$\gamma\in\pi_1(S)$
whose characteristic polynomials are of the form f(t) or
![]() $(t-1)f(t)$
for some irreducible f(t) in
$(t-1)f(t)$
for some irreducible f(t) in
![]() $\mathcal{O}_K[t]$
. When such
$\mathcal{O}_K[t]$
. When such
![]() $\gamma$
cannot be found, we then use the reducibility of the characteristic polynomials to explicitly construct bending matrices we may use as well. The methods used in constructing these matrices vary depending on what the input to the bend is, particularly, what the number field K is, and what the Zariski closure of the initial representation
$\gamma$
cannot be found, we then use the reducibility of the characteristic polynomials to explicitly construct bending matrices we may use as well. The methods used in constructing these matrices vary depending on what the input to the bend is, particularly, what the number field K is, and what the Zariski closure of the initial representation
![]() $\rho(\pi_1(S))$
is.
$\rho(\pi_1(S))$
is.
4·1. Bending when
 $K\neq\mathbf{Q}$
$K\neq\mathbf{Q}$
The simplest case of the bending procedure occurs when K is a proper extension of
![]() $\mathbf{Q}$
with class number one. In this case, we are able to prove the following strengthening of Theorem 1·1.
$\mathbf{Q}$
with class number one. In this case, we are able to prove the following strengthening of Theorem 1·1.
Theorem 4·4. If
![]() $K\neq \mathbf{Q}$
and
$K\neq \mathbf{Q}$
and
![]() $\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathcal{O}_K)$
is a representation on the Hitchin component whose image is not Zariski dense, then for any nonseparating simple closed curve
$\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathcal{O}_K)$
is a representation on the Hitchin component whose image is not Zariski dense, then for any nonseparating simple closed curve
![]() $\gamma\in\pi_1(S)$
, there is an
$\gamma\in\pi_1(S)$
, there is an
![]() $A\in\textrm{SL}(n,\mathcal{O}_K)$
centralizing
$A\in\textrm{SL}(n,\mathcal{O}_K)$
centralizing
![]() $\rho(\gamma)$
so that the bent representation
$\rho(\gamma)$
so that the bent representation
![]() $\rho^A$
is on the Hitchin component and has Zariski dense image.
$\rho^A$
is on the Hitchin component and has Zariski dense image.
In comparison to Theorem 1·1, when
![]() $K\neq \mathbf{Q}$
, we are able to ensure the representation is Zariski dense while circumventing the need to pass to any finite sheeted covers. The class number one hypothesis enables various integrality properties to be preserved, but the proof of this result is ultimately enabled by the presence of infinite order units in
$K\neq \mathbf{Q}$
, we are able to ensure the representation is Zariski dense while circumventing the need to pass to any finite sheeted covers. The class number one hypothesis enables various integrality properties to be preserved, but the proof of this result is ultimately enabled by the presence of infinite order units in
![]() $\mathcal{O}_K$
allowing one to construct the bending matrix A explicitly.
$\mathcal{O}_K$
allowing one to construct the bending matrix A explicitly.
Proof of
4·4. For any nonseparating simple closed
![]() $\gamma\in\pi_1(S)$
, we consider the characteristic polynomial f, of
$\gamma\in\pi_1(S)$
, we consider the characteristic polynomial f, of
![]() $\rho(\gamma)$
. If f is irreducible, then we take the matrix A to be the one guaranteed by Lemma 4·2. As A doesn’t preserve the (unique) form J which
$\rho(\gamma)$
. If f is irreducible, then we take the matrix A to be the one guaranteed by Lemma 4·2. As A doesn’t preserve the (unique) form J which
![]() $\rho(\pi_1(S))$
must preserve (as in Lemma 3·1), then
$\rho(\pi_1(S))$
must preserve (as in Lemma 3·1), then
![]() $\rho^A(\pi_1(S))$
must have Zariski closure larger than
$\rho^A(\pi_1(S))$
must have Zariski closure larger than
![]() $\textrm{SO}(J;\, \mathbf{R})$
or
$\textrm{SO}(J;\, \mathbf{R})$
or
![]() $\textrm{Sp}(J;\, \mathbf{R})$
and so it must be Zariski dense by Theorem 2·3.
$\textrm{Sp}(J;\, \mathbf{R})$
and so it must be Zariski dense by Theorem 2·3.
Thus we may assume that f is reducible over
![]() $\mathcal{O}_K$
. It suffices to assume that
$\mathcal{O}_K$
. It suffices to assume that
![]() $f=f_1 f_2$
for
$f=f_1 f_2$
for
![]() $f_i\in\mathcal{O}_K[t]$
of degree
$f_i\in\mathcal{O}_K[t]$
of degree
![]() $n_1,n_2\geq 1$
respectively. Replacing
$n_1,n_2\geq 1$
respectively. Replacing
![]() $f_1$
and
$f_1$
and
![]() $f_2$
with
$f_2$
with
![]() $uf_1$
and
$uf_1$
and
![]() $u^{-1}f_2$
for some unit
$u^{-1}f_2$
for some unit
![]() $u\in\mathcal{O}_K^\times$
if necessary, we may also assume that
$u\in\mathcal{O}_K^\times$
if necessary, we may also assume that
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are monic and have constant terms
$f_2$
are monic and have constant terms
![]() $({-}1)^{n_1}$
and
$({-}1)^{n_1}$
and
![]() $({-}1)^{n_2}$
respectively. From the factorisation of the characteristic polynomial, there is some matrix
$({-}1)^{n_2}$
respectively. From the factorisation of the characteristic polynomial, there is some matrix
![]() $P\in\textrm{GL}(n,K)$
so that
$P\in\textrm{GL}(n,K)$
so that
where for
![]() $i=1,2$
,
$i=1,2$
,
![]() $C_i\in\textrm{SL}(n_i,\mathcal{O}_K)$
has characteristic polynomial
$C_i\in\textrm{SL}(n_i,\mathcal{O}_K)$
has characteristic polynomial
![]() $f_i$
. Here, we are using the fact that the factorization of f is over
$f_i$
. Here, we are using the fact that the factorization of f is over
![]() $\mathcal{O}_K$
and that K has class number one to guarantee that the entries of the
$\mathcal{O}_K$
and that K has class number one to guarantee that the entries of the
![]() $C_i$
are indeed in
$C_i$
are indeed in
![]() $\mathcal{O}_K$
, as in the proof of Lemma 4·1.
$\mathcal{O}_K$
, as in the proof of Lemma 4·1.
Now, as
![]() $K\neq\mathbf{Q}$
,
$K\neq\mathbf{Q}$
,
![]() $[K\,:\,\mathbf{Q}]\gt1$
. Assuming
$[K\,:\,\mathbf{Q}]\gt1$
. Assuming
![]() $K\subset\mathbf{R}$
also forces K to have
$K\subset\mathbf{R}$
also forces K to have
![]() $\geq 1$
real embeddings, and together, this forces
$\geq 1$
real embeddings, and together, this forces
![]() $\mathcal{O}_K^\times$
to have rank
$\mathcal{O}_K^\times$
to have rank
![]() $\geq 1$
. We may thus fix an infinite order unit
$\geq 1$
. We may thus fix an infinite order unit
![]() $u\in\mathcal{O}_K^\times$
and, replacing u with
$u\in\mathcal{O}_K^\times$
and, replacing u with
![]() $-u$
if necessary, we may also assume that
$-u$
if necessary, we may also assume that
![]() $u\gt0$
.
$u\gt0$
.
In this case, we take the matrix
![]() $A'\in\textrm{SL}(n,K)$
has characteristic polynomial still in
$A'\in\textrm{SL}(n,K)$
has characteristic polynomial still in
![]() $\mathcal{O}_K[t]$
and clearly centralizes
$\mathcal{O}_K[t]$
and clearly centralizes
![]() $\rho(\gamma)$
due to
$\rho(\gamma)$
due to
![]() $PA' P^{-1}$
having the same block-diagonal structure as
$PA' P^{-1}$
having the same block-diagonal structure as
![]() $P\rho(\gamma)P^{-1}$
. As
$P\rho(\gamma)P^{-1}$
. As
![]() $u\gt0$
and
$u\gt0$
and
![]() $C_2$
is diagonalisable,
$C_2$
is diagonalisable,
![]() $A'=\exp(X)$
for some diagonalisable
$A'=\exp(X)$
for some diagonalisable
![]() $X\in\mathfrak{sl}(n,\mathbf{R})$
as well. Note as well that A
′ does not preserve the form J as its eigenvalues are
$X\in\mathfrak{sl}(n,\mathbf{R})$
as well. Note as well that A
′ does not preserve the form J as its eigenvalues are
![]() $u^{n_2}$
(with multiplicity
$u^{n_2}$
(with multiplicity
![]() $n_1$
) and
$n_1$
) and
![]() $u^{-n_1}\lambda$
where
$u^{-n_1}\lambda$
where
![]() $\lambda$
is any of the (distinct, real) eigenvalues of
$\lambda$
is any of the (distinct, real) eigenvalues of
![]() $C_2$
, and these eigenvalues do not pair up as needed for any matrix preserving the form J.
$C_2$
, and these eigenvalues do not pair up as needed for any matrix preserving the form J.
Passing to a higher power of A’ by Lemma 4·1,
![]() $A=(A')^{\kern1pt j}\in\textrm{SL}(n,\mathcal{O}_K)$
for sufficiently large j still centralises
$A=(A')^{\kern1pt j}\in\textrm{SL}(n,\mathcal{O}_K)$
for sufficiently large j still centralises
![]() $\rho(\gamma)$
and remains the exponential of some diagonalisable matrix. As u is an infinite order unit, A will still fail to preserve the form J as A
′ did. Therefore, by Lemma 3·1, the bent representation
$\rho(\gamma)$
and remains the exponential of some diagonalisable matrix. As u is an infinite order unit, A will still fail to preserve the form J as A
′ did. Therefore, by Lemma 3·1, the bent representation
![]() $\rho^A$
has Zariski dense image.
$\rho^A$
has Zariski dense image.
By handling the
![]() $K\neq\mathbf{Q}$
case separately using the presence of infinite order units in
$K\neq\mathbf{Q}$
case separately using the presence of infinite order units in
![]() $\mathcal{O}_K$
, we may then assume that
$\mathcal{O}_K$
, we may then assume that
![]() $K=\mathbf{Q}$
and
$K=\mathbf{Q}$
and
![]() $\mathcal{O}_K=\mathbf{Z}$
for the remainder of this section.
$\mathcal{O}_K=\mathbf{Z}$
for the remainder of this section.
4·2. Bending out of a principal
 $\textrm{SL}(2,\mathbf{R})$
$\textrm{SL}(2,\mathbf{R})$
When
![]() $K=\mathbf{Q}$
, no infinite order units are present and so an alternate method is necessary. The overall construction of the bending matrices here is then a two-fold process: one to bend the representation out of a principal
$K=\mathbf{Q}$
, no infinite order units are present and so an alternate method is necessary. The overall construction of the bending matrices here is then a two-fold process: one to bend the representation out of a principal
![]() $\textrm{SL}(2,\mathbf{R})$
and a second to bend the representation out of either
$\textrm{SL}(2,\mathbf{R})$
and a second to bend the representation out of either
![]() $\textrm{Sp}(2k,\mathbf{R})$
or
$\textrm{Sp}(2k,\mathbf{R})$
or
![]() $\textrm{SO}(k+1,k)$
to finally get a representation with Zariski dense image in
$\textrm{SO}(k+1,k)$
to finally get a representation with Zariski dense image in
![]() $\textrm{SL}(n,\mathbf{R})$
. Different methods are used for each bend, the simpler one when the Zariski closure of
$\textrm{SL}(n,\mathbf{R})$
. Different methods are used for each bend, the simpler one when the Zariski closure of
![]() $\rho(\pi_1(S))$
is “as small as possible.”
$\rho(\pi_1(S))$
is “as small as possible.”
By Theorem 2·3, the smallest possible Zariski closure that our representation might have is that of a principal
![]() $\textrm{SL}(2,\mathbf{R})$
inside of
$\textrm{SL}(2,\mathbf{R})$
inside of
![]() $\textrm{SL}(n,\mathbf{R})$
. So suppose that
$\textrm{SL}(n,\mathbf{R})$
. So suppose that
![]() $\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{Z})$
has Zariski closure conjugate to
$\rho\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{Z})$
has Zariski closure conjugate to
![]() $\tau_n(\textrm{SL}(2,\mathbf{R}))$
. In this case, we start by fixing any nonseparating simple closed curve
$\tau_n(\textrm{SL}(2,\mathbf{R}))$
. In this case, we start by fixing any nonseparating simple closed curve
![]() $\gamma\in\pi_1(S)$
.
$\gamma\in\pi_1(S)$
.
By Theorem 2·1,
![]() $\rho(\gamma)$
is diagonalisable with distinct real eigenvalues. Moreover, as
$\rho(\gamma)$
is diagonalisable with distinct real eigenvalues. Moreover, as
![]() $\rho(\pi_1(S))$
is contained in some principal
$\rho(\pi_1(S))$
is contained in some principal
![]() $\textrm{SL}(2,\mathbf{R})$
, basic properties about the irreducible representations of
$\textrm{SL}(2,\mathbf{R})$
, basic properties about the irreducible representations of
![]() $\textrm{SL}(2,\mathbf{R})$
tell us that the eigenvalues of
$\textrm{SL}(2,\mathbf{R})$
tell us that the eigenvalues of
![]() $\rho(\gamma)$
are of the form
$\rho(\gamma)$
are of the form
![]() $\lambda^{n-2i-1}$
for
$\lambda^{n-2i-1}$
for
![]() $i=0,\ldots,n-1$
. In this case, the characteristic polynomial of
$i=0,\ldots,n-1$
. In this case, the characteristic polynomial of
![]() $\rho(\gamma)$
is of the form
$\rho(\gamma)$
is of the form
![]() $(t-1)f(t)$
or f(t) for some
$(t-1)f(t)$
or f(t) for some
![]() $f\in\mathbf{Z}[t]$
depending on the parity of n. If f(t) is irreducible in either of the above cases, we again apply Lemma 4·2 to construct the matrix A (in the n odd case, we proceed as in the remark after Lemma 4·2). Consequently, the matrix A provided by this theorem does not preserve the form this principal
$f\in\mathbf{Z}[t]$
depending on the parity of n. If f(t) is irreducible in either of the above cases, we again apply Lemma 4·2 to construct the matrix A (in the n odd case, we proceed as in the remark after Lemma 4·2). Consequently, the matrix A provided by this theorem does not preserve the form this principal
![]() $\textrm{SL}(2,\mathbf{R})$
does, and so
$\textrm{SL}(2,\mathbf{R})$
does, and so
![]() $\rho^A$
will then have Zariski dense image. So just as with the
$\rho^A$
will then have Zariski dense image. So just as with the
![]() $K\neq \mathbf{Q}$
construction, we are able to guarantee the representation has Zariski dense image after a single bend, if we can find a
$K\neq \mathbf{Q}$
construction, we are able to guarantee the representation has Zariski dense image after a single bend, if we can find a
![]() $\gamma\in\pi_1(S)$
with this property.
$\gamma\in\pi_1(S)$
with this property.
What remains in this case is when f(t) is reducible over
![]() $\mathbf{Z}$
. That is, we may assume the characteristic polynomial of
$\mathbf{Z}$
. That is, we may assume the characteristic polynomial of
![]() $\rho(\gamma)$
admits a factorisation of the form
$\rho(\gamma)$
admits a factorisation of the form
for polynomials
![]() $f_1,f_2\in\mathbf{Z}[t]$
of degree
$f_1,f_2\in\mathbf{Z}[t]$
of degree
![]() $n_1,n_2\geq 1$
respectively. From the factorization of the characteristic polynomial, it follows then that there is some matrix
$n_1,n_2\geq 1$
respectively. From the factorization of the characteristic polynomial, it follows then that there is some matrix
![]() $P\in\textrm{GL}(n,\mathbf{Q})$
so that
$P\in\textrm{GL}(n,\mathbf{Q})$
so that
 \[P\rho(\gamma)P^{-1}=\begin{cases}\displaystyle\begin{pmatrix}1 \\& C_1\\&&C_2\end{pmatrix} & \textrm{if}\ \textit{n}\ \textrm{is odd}\\\displaystyle\begin{pmatrix} C_1\\&C_2\end{pmatrix} & \textrm{if}\ \textit{n}\ \textrm{is even,}\end{cases}\]
\[P\rho(\gamma)P^{-1}=\begin{cases}\displaystyle\begin{pmatrix}1 \\& C_1\\&&C_2\end{pmatrix} & \textrm{if}\ \textit{n}\ \textrm{is odd}\\\displaystyle\begin{pmatrix} C_1\\&C_2\end{pmatrix} & \textrm{if}\ \textit{n}\ \textrm{is even,}\end{cases}\]
where for
![]() $i=1$
or 2,
$i=1$
or 2,
![]() $C_i\in \textrm{SL}(n_i,\mathbf{Z})$
has characteristic polynomial
$C_i\in \textrm{SL}(n_i,\mathbf{Z})$
has characteristic polynomial
![]() $f_i$
. We now take A
′ to be the matrix
$f_i$
. We now take A
′ to be the matrix
 \[A'=\begin{cases}\displaystyle P^{-1}\begin{pmatrix} 1\\&I_{n_1}\\&&C_2\end{pmatrix}P &\textrm{if}\ \textit{n}\ \textrm{is odd}\\\displaystyle P^{-1}\begin{pmatrix} I_{n_1}\\&C_2\end{pmatrix} P&\textrm{if}\ \textit{n}\ \textrm{is even.}\end{cases}\]
\[A'=\begin{cases}\displaystyle P^{-1}\begin{pmatrix} 1\\&I_{n_1}\\&&C_2\end{pmatrix}P &\textrm{if}\ \textit{n}\ \textrm{is odd}\\\displaystyle P^{-1}\begin{pmatrix} I_{n_1}\\&C_2\end{pmatrix} P&\textrm{if}\ \textit{n}\ \textrm{is even.}\end{cases}\]
Note that in both cases,
![]() $\det(A')=\det(C_2)=1$
and A’ is in the
$\det(A')=\det(C_2)=1$
and A’ is in the
![]() $\mathbf{Q}$
-centraliser of
$\mathbf{Q}$
-centraliser of
![]() $\rho(\gamma)$
.
$\rho(\gamma)$
.
By Lemma 4·1 there is some
![]() $j\gt0$
so that
$j\gt0$
so that
![]() $(A')^j$
has entries in
$(A')^j$
has entries in
![]() $\mathbf{Z}$
. We take
$\mathbf{Z}$
. We take
![]() $A=(A')^j$
. Then by construction,
$A=(A')^j$
. Then by construction,
![]() $A\in\textrm{SL}(n,\mathbf{Z})$
centralises
$A\in\textrm{SL}(n,\mathbf{Z})$
centralises
![]() $\rho(\gamma)$
. Moreover, A is not contained in a principal
$\rho(\gamma)$
. Moreover, A is not contained in a principal
![]() $\textrm{SL}(2,\mathbf{R})$
because the eigenvalues of A are not of the form
$\textrm{SL}(2,\mathbf{R})$
because the eigenvalues of A are not of the form
![]() $\mu^{n-2i-1}$
for some
$\mu^{n-2i-1}$
for some
![]() $\mu\in\mathbf{R}$
since A has an eigenvalue 1 of multiplicity
$\mu\in\mathbf{R}$
since A has an eigenvalue 1 of multiplicity
![]() $\gt1$
. Finally, we show that A is in the image of the exponential map. For this, it suffices to show
$\gt1$
. Finally, we show that A is in the image of the exponential map. For this, it suffices to show
![]() $A'=\exp(X)$
for some
$A'=\exp(X)$
for some
![]() $X\in\mathfrak{sl}(n,\mathbf{R})$
since then,
$X\in\mathfrak{sl}(n,\mathbf{R})$
since then,
![]() $A=(A')^j=\exp(jX)$
. In this case, if we let
$A=(A')^j=\exp(jX)$
. In this case, if we let
![]() $\lambda_1,\ldots,\lambda_{n_2}$
be the distinct positive real eigenvalues of
$\lambda_1,\ldots,\lambda_{n_2}$
be the distinct positive real eigenvalues of
![]() $C_2$
, then
$C_2$
, then
![]() $C_2$
is diagonalisable over
$C_2$
is diagonalisable over
![]() $\mathbf{R}$
and we have that
$\mathbf{R}$
and we have that
 \[A'=Q^{-1}\exp\begin{pmatrix}0\\&\ddots\\&&0\\&&&\log(\lambda_1)\\&&&&\ddots\\&&&&&\log(\lambda_{n_2})\end{pmatrix}Q\]
\[A'=Q^{-1}\exp\begin{pmatrix}0\\&\ddots\\&&0\\&&&\log(\lambda_1)\\&&&&\ddots\\&&&&&\log(\lambda_{n_2})\end{pmatrix}Q\]
for some
![]() $Q\in\textrm{GL}(n,\mathbf{R})$
. Moreover,
$Q\in\textrm{GL}(n,\mathbf{R})$
. Moreover,
![]() $\det(C_2)=1$
so that the trace of the above matrix is 0, hence
$\det(C_2)=1$
so that the trace of the above matrix is 0, hence
![]() $A'=\exp(X)$
for some diagonalisable
$A'=\exp(X)$
for some diagonalisable
![]() $X\in\mathfrak{sl}(n,\mathbf{R})$
.
$X\in\mathfrak{sl}(n,\mathbf{R})$
.
As a result, the matrix A centralising
![]() $\rho(\gamma)$
can be used to bend the representation
$\rho(\gamma)$
can be used to bend the representation
![]() $\rho$
and produce a representation
$\rho$
and produce a representation
![]() $\rho^A\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{Z})$
on the Hitchin component with Zariski closure strictly larger than a principal
$\rho^A\,:\,\pi_1(S)\to\textrm{SL}(n,\mathbf{Z})$
on the Hitchin component with Zariski closure strictly larger than a principal
![]() $\textrm{SL}(2,\mathbf{R})$
. At this point, the resulting bent representation may still have Zariski closure conjugate to
$\textrm{SL}(2,\mathbf{R})$
. At this point, the resulting bent representation may still have Zariski closure conjugate to
![]() $\textrm{SO}(k+1,k)$
or
$\textrm{SO}(k+1,k)$
or
![]() $\textrm{Sp}(2k,\mathbf{R})$
when
$\textrm{Sp}(2k,\mathbf{R})$
when
![]() $n=2k+1$
or
$n=2k+1$
or
![]() $n=2k$
respectively. Thus another bend is still necessary to guarantee that one may produce a final representation with Zariski dense image.
$n=2k$
respectively. Thus another bend is still necessary to guarantee that one may produce a final representation with Zariski dense image.
4·3. Bending out of
 $\textrm{Sp}(2k,\mathbf{R})$
$\textrm{Sp}(2k,\mathbf{R})$
We handle the even case first which follows the same general strategy as the bend out of
![]() $\textrm{SO}(k+1,k)$
, but is practically easier, due to facts about symplectic groups which simplify various steps. Assume that
$\textrm{SO}(k+1,k)$
, but is practically easier, due to facts about symplectic groups which simplify various steps. Assume that
![]() $\rho\,:\,\pi_1(S)\to\textrm{SL}(2k,\mathbf{Z})$
has Zariski closure
$\rho\,:\,\pi_1(S)\to\textrm{SL}(2k,\mathbf{Z})$
has Zariski closure
![]() $\textrm{Sp}(2k,\mathbf{R})$
. The starting point is the following Strong Approximation result from the theory of algebraic groups.
$\textrm{Sp}(2k,\mathbf{R})$
. The starting point is the following Strong Approximation result from the theory of algebraic groups.
Theorem 4·5 (Matthews et al., [Reference Matthews, Vaserstein and Weisfeiler21]). Let G be a connected simply-connected absolutely almost simple algebraic group defined over
![]() $\mathbf{Q}$
and
$\mathbf{Q}$
and
![]() $\Gamma\leqslant G(\mathbf{Q})$
a finitely generated Zariski dense subgroup.
$\Gamma\leqslant G(\mathbf{Q})$
a finitely generated Zariski dense subgroup.
Then for all but finitely many primes p, the reduction map
is onto.
We will also need the following result, attributed to Borel ([Reference Chavdarov6, theorem 3·5 and corollary 3·6]).
Theorem 4·6 (Borel, cf. [Reference Chavdarov6]). Let
![]() $p\gt4$
and let
$p\gt4$
and let
![]() $R_p(2k)$
be the set of
$R_p(2k)$
be the set of
![]() $2k\times 2k$
matrices in
$2k\times 2k$
matrices in
![]() $\textrm{Sp}(2k,\mathbf{F}_p)$
with reducible characteristic polynomial. Then
$\textrm{Sp}(2k,\mathbf{F}_p)$
with reducible characteristic polynomial. Then
By Theorem 4·5 for
![]() $G=\textrm{Sp}(2k)$
and
$G=\textrm{Sp}(2k)$
and
![]() $\Gamma=\rho(\pi_1(S))$
, we obtain a surjection
$\Gamma=\rho(\pi_1(S))$
, we obtain a surjection
for some prime p which, when combined with Theorem 4.6, implies there exists some loop
![]() $\eta\in\pi_1(S)$
so that the characteristic polynomial of
$\eta\in\pi_1(S)$
so that the characteristic polynomial of
![]() $\pi_p(\rho(\eta))$
is irreducible modulo p. Consequently,
$\pi_p(\rho(\eta))$
is irreducible modulo p. Consequently,
![]() $\rho(\eta)$
has characteristic polynomial irreducible over
$\rho(\eta)$
has characteristic polynomial irreducible over
![]() $\mathbf{Z}$
. Now, at the moment, this loop may not be simple, but the following result allows us to remedy this.
$\mathbf{Z}$
. Now, at the moment, this loop may not be simple, but the following result allows us to remedy this.
Theorem 4·7 (Scott, [Reference Scott25]). Every closed curve on S lifts to a simple closed curve in some finite-sheeted cover.
We now pass to a finite sheeted cover
![]() $\widetilde{S}\to S$
where
$\widetilde{S}\to S$
where
![]() $\eta$
lifts simply and restrict our representation
$\eta$
lifts simply and restrict our representation
![]() $\rho$
, to the subgroup
$\rho$
, to the subgroup
![]() $\pi_1(\widetilde{S})\leqslant\pi_1(S)$
. By passing to a further finite sheeted cover if needed, we may also assume that the loop
$\pi_1(\widetilde{S})\leqslant\pi_1(S)$
. By passing to a further finite sheeted cover if needed, we may also assume that the loop
![]() $\eta\in\pi_1(\widetilde{S})$
is nonseparating. The following lemma is needed before then performing the bend out of
$\eta\in\pi_1(\widetilde{S})$
is nonseparating. The following lemma is needed before then performing the bend out of
![]() $\textrm{Sp}(2k,\mathbf{R})$
.
$\textrm{Sp}(2k,\mathbf{R})$
.
Lemma 4·8. The subgroup
![]() $\rho(\pi_1(\widetilde{S}))\leqslant\rho(\pi_1(S))$
has Zariski closure
$\rho(\pi_1(\widetilde{S}))\leqslant\rho(\pi_1(S))$
has Zariski closure
![]() $\textrm{Sp}(2k,\mathbf{R})$
.
$\textrm{Sp}(2k,\mathbf{R})$
.
Proof. Let H denote the Zariski closure of
![]() $\rho(\pi_1(\widetilde{S}))$
. Clearly
$\rho(\pi_1(\widetilde{S}))$
. Clearly
![]() $H\leqslant\textrm{Sp}(2k,\mathbf{R})$
, but as
$H\leqslant\textrm{Sp}(2k,\mathbf{R})$
, but as
![]() $\widetilde{S}$
is still a closed surface and
$\widetilde{S}$
is still a closed surface and
![]() $\rho|_{\pi_1(\widetilde{S})}$
lies on the Hitchin component of
$\rho|_{\pi_1(\widetilde{S})}$
lies on the Hitchin component of
![]() $\widetilde{S}$
, Guichard’s classification (Theorem 2·3) implies that either
$\widetilde{S}$
, Guichard’s classification (Theorem 2·3) implies that either
![]() $H=\textrm{Sp}(2k,\mathbf{R})$
or H is a principal
$H=\textrm{Sp}(2k,\mathbf{R})$
or H is a principal
![]() $\textrm{SL}(2,\mathbf{R})$
.
$\textrm{SL}(2,\mathbf{R})$
.
But H is of finite index in G, so if
![]() $g_1,\ldots,g_k$
are finitely many coset representatives for
$g_1,\ldots,g_k$
are finitely many coset representatives for
![]() $G/H$
, then
$G/H$
, then
![]() $g_1 H\cup\ldots\cup g_kH$
is a Zariski-closed subset containing G. If H was a principal
$g_1 H\cup\ldots\cup g_kH$
is a Zariski-closed subset containing G. If H was a principal
![]() $\textrm{SL}(2,\mathbf{R})$
, this would imply that
$\textrm{SL}(2,\mathbf{R})$
, this would imply that
![]() $\textrm{Sp}(2k,\mathbf{R})$
is a union of finitely many principal
$\textrm{Sp}(2k,\mathbf{R})$
is a union of finitely many principal
![]() $\textrm{SL}(2,\mathbf{R})$
’s and simply for dimension reasons this is even impossible.
$\textrm{SL}(2,\mathbf{R})$
’s and simply for dimension reasons this is even impossible.
By this lemma, we have a representation
![]() $\rho\,:\,\pi_1(\widetilde{S})\to\textrm{SL}(n,\mathbf{Z})$
which is Zariski dense in
$\rho\,:\,\pi_1(\widetilde{S})\to\textrm{SL}(n,\mathbf{Z})$
which is Zariski dense in
![]() $\textrm{Sp}(2k,\mathbf{R})$
and on the Hitchin component of
$\textrm{Sp}(2k,\mathbf{R})$
and on the Hitchin component of
![]() $\widetilde{S}$
. Moreover, the curve
$\widetilde{S}$
. Moreover, the curve
![]() $\eta\in\pi_1(S)$
lifts simply in
$\eta\in\pi_1(S)$
lifts simply in
![]() $\widetilde{S}$
and the characteristic polynomial of
$\widetilde{S}$
and the characteristic polynomial of
![]() $\eta$
is irreducible over
$\eta$
is irreducible over
![]() $\mathbf{Z}$
. In light of Lemma 4·2, there is some bending matrix
$\mathbf{Z}$
. In light of Lemma 4·2, there is some bending matrix
![]() $A\in\textrm{SL}(n,\mathbf{Z})$
so that the bent representation
$A\in\textrm{SL}(n,\mathbf{Z})$
so that the bent representation
![]() $\rho^A$
is Zariski dense in
$\rho^A$
is Zariski dense in
![]() $\textrm{SL}(n,\mathbf{R})$
.
$\textrm{SL}(n,\mathbf{R})$
.
4·4. Bending out of
 $\textrm{SO}(k+1,k)$
$\textrm{SO}(k+1,k)$
In the odd n case, the only possible representations remaining are the
![]() $\mathbf{Q}$
-integral ones with Zariski closure conjugate to
$\mathbf{Q}$
-integral ones with Zariski closure conjugate to
![]() $\textrm{SO}(k+1,k)$
. Suppose that
$\textrm{SO}(k+1,k)$
. Suppose that
![]() $\rho\,:\,\pi_1(S)\to\textrm{SL}(2k+1,\mathbf{Z})$
has Zariski closure
$\rho\,:\,\pi_1(S)\to\textrm{SL}(2k+1,\mathbf{Z})$
has Zariski closure
![]() $\textrm{SO}(J;\, \mathbf{R})$
where J is some symmetric bilinear form of signature
$\textrm{SO}(J;\, \mathbf{R})$
where J is some symmetric bilinear form of signature
![]() $(k+1,k)$
. In this case, we prove the following fact.
$(k+1,k)$
. In this case, we prove the following fact.
Lemma 4·9. There exists a
![]() $\eta\in\pi_1(S)$
so that
$\eta\in\pi_1(S)$
so that
![]() $\rho(\eta)$
has characteristic polynomial
$\rho(\eta)$
has characteristic polynomial
![]() $(t-1)f(t)\in\mathbf{Z}[t]$
with f(t) irreducible over
$(t-1)f(t)\in\mathbf{Z}[t]$
with f(t) irreducible over
![]() $\mathbf{Z}$
.
$\mathbf{Z}$
.
The required loop is constructed in essentially the same manner as done in [Reference Long and Thistlethwaite19, section 3·2], but we recap the construction, and note the minor differences here. Again, the first step will be to look at the reduction map
![]() $\textrm{SO}(J,\mathbf{Z})\to\textrm{SO}(J,\mathbf{F}_p)$
for some prime p. In this case, over odd-dimensional vector spaces over finite fields, there is a unique orthogonal group up to isomorphism, dependent only on the dimension and the prime p [Reference Suzuki26, theorem 5·8]. Thus we will make the identification
$\textrm{SO}(J,\mathbf{Z})\to\textrm{SO}(J,\mathbf{F}_p)$
for some prime p. In this case, over odd-dimensional vector spaces over finite fields, there is a unique orthogonal group up to isomorphism, dependent only on the dimension and the prime p [Reference Suzuki26, theorem 5·8]. Thus we will make the identification
![]() $\text{O}(J,\mathbf{F}_p)=\text{O}(2k+1,p)$
. In this case, we let
$\text{O}(J,\mathbf{F}_p)=\text{O}(2k+1,p)$
. In this case, we let
![]() $\textrm{SO}(2k+1,p)$
denote the (unique up to isomorphism) special orthogonal group over
$\textrm{SO}(2k+1,p)$
denote the (unique up to isomorphism) special orthogonal group over
![]() $\mathbf{F}_p$
and also set
$\mathbf{F}_p$
and also set
![]() $\Omega(2k+1,p)=[\text{O}(2k+1,p),\text{O}(2k+1,p)]\leqslant\textrm{SO}(2k+1,p)$
to be the commutator subgroup.
$\Omega(2k+1,p)=[\text{O}(2k+1,p),\text{O}(2k+1,p)]\leqslant\textrm{SO}(2k+1,p)$
to be the commutator subgroup.
![]() $\Omega(2k+1,p)$
is a simple subgroup of index 4 in
$\Omega(2k+1,p)$
is a simple subgroup of index 4 in
![]() $\text{O}(2k+1,p)$
(cf. [Reference Suzuki26], p. 383–384).
$\text{O}(2k+1,p)$
(cf. [Reference Suzuki26], p. 383–384).
Just as in Section 4.3, the curve in Lemma 4·9 with the required characteristic polynomial will be constructed by looking at the characteristic polynomials modulo some prime p. However, we can’t simply apply Strong Approximation as is stated in Theorem 4·5 simply due to the fact that the algebraic group
![]() $\textrm{SO}(J)$
is not simply connected. Instead, the following corollary of Strong Approximation (cf. [Reference Weisfeiler27]) still provides us with enough in the image of the reduction map to construct the needed
$\textrm{SO}(J)$
is not simply connected. Instead, the following corollary of Strong Approximation (cf. [Reference Weisfeiler27]) still provides us with enough in the image of the reduction map to construct the needed
![]() $\eta$
.
$\eta$
.
Theorem 4·10. For all but finitely many primes p, the image of the composition
contains the subgroup
![]() $\Omega(2k+1,p)$
.
$\Omega(2k+1,p)$
.
Lemma 4·9 then follows immediately from the previous theorem and the following result whose proof is [Reference Long and Thistlethwaite19 theorem 3.8].
Lemma 4·11. For every prime p, there is a matrix in
![]() $\Omega(2k+1,p)$
with a characteristic polynomial of the form
$\Omega(2k+1,p)$
with a characteristic polynomial of the form
![]() $(t-1)\overline{f}(t)$
where
$(t-1)\overline{f}(t)$
where
![]() $\overline{f}$
is irreducible modulo p.
$\overline{f}$
is irreducible modulo p.
By these last two results, we may find some
![]() $\eta\in\pi_1(S)$
so that
$\eta\in\pi_1(S)$
so that
![]() $\pi_p(\rho(\eta))$
has characteristic polynomial of the form
$\pi_p(\rho(\eta))$
has characteristic polynomial of the form
![]() $(t-1)\overline{f}(t)$
for some
$(t-1)\overline{f}(t)$
for some
![]() $\overline{f}$
irreducible modulo p. It follows that
$\overline{f}$
irreducible modulo p. It follows that
![]() $\rho(\eta)$
has characteristic polynomial of the form
$\rho(\eta)$
has characteristic polynomial of the form
![]() $(t-1)f(t)$
for some f irreducible over
$(t-1)f(t)$
for some f irreducible over
![]() $\mathbf{Z}$
. As before,
$\mathbf{Z}$
. As before,
![]() $\eta$
may not be simple, but Theorem 4·7 again lets us pass to a finite sheeted cover
$\eta$
may not be simple, but Theorem 4·7 again lets us pass to a finite sheeted cover
![]() $\widetilde{S}\to S$
where
$\widetilde{S}\to S$
where
![]() $\eta$
lifts simply to a nonseparating curve. Again, as in Lemma 4.8,
$\eta$
lifts simply to a nonseparating curve. Again, as in Lemma 4.8,
![]() $\rho(\pi_1(\widetilde{S}))\leqslant\rho(\pi_1(S))$
also has Zariski closure
$\rho(\pi_1(\widetilde{S}))\leqslant\rho(\pi_1(S))$
also has Zariski closure
![]() $\textrm{SO}(J;\, \mathbf{R})$
and so we may perform the bend on the restriction
$\textrm{SO}(J;\, \mathbf{R})$
and so we may perform the bend on the restriction
![]() $\rho\,:\,\pi_1(\widetilde{S})\to\textrm{SL}(n,\mathbf{Z})$
, along the simple closed curve
$\rho\,:\,\pi_1(\widetilde{S})\to\textrm{SL}(n,\mathbf{Z})$
, along the simple closed curve
![]() $\eta$
, to get a representation
$\eta$
, to get a representation
![]() $\rho^A:\pi_1(\widetilde{S})\to\textrm{SL}(n,\mathbf{Z})$
with Zariski dense image in
$\rho^A:\pi_1(\widetilde{S})\to\textrm{SL}(n,\mathbf{Z})$
with Zariski dense image in
![]() $\textrm{SL}(n,\mathbf{R})$
via Lemma 4·2. This last remaining case then completes the proof of Theorem 1·1.
$\textrm{SL}(n,\mathbf{R})$
via Lemma 4·2. This last remaining case then completes the proof of Theorem 1·1.
5. Applications
The methods of this paper also have a number of useful consequences and applications. We record some of these here.
Corollary 5·1. If
![]() $\textrm{Hit}_n(S)$
contains an
$\textrm{Hit}_n(S)$
contains an
![]() $\mathcal{O}_K$
-point, then there are infinitely many
$\mathcal{O}_K$
-point, then there are infinitely many
![]() $\mathcal{O}_K$
-points in
$\mathcal{O}_K$
-points in
![]() $\textrm{Hit}_n(S)$
which are Zariski dense.
$\textrm{Hit}_n(S)$
which are Zariski dense.
Proof. This mainly is a consequence of the fact that the construction of the bending matrices A rely on a number of arbitrary choices made, and any difference in these choices lead to different Zariski dense representations of
![]() $\pi_1(S)$
. For instance, if A is a bending matrix satisfying properties (a)–(c) used in the proof of Theorem 1·1, then so is
$\pi_1(S)$
. For instance, if A is a bending matrix satisfying properties (a)–(c) used in the proof of Theorem 1·1, then so is
![]() $A^m$
for any integer
$A^m$
for any integer
![]() $m\geq 1$
, and hence
$m\geq 1$
, and hence
![]() $\rho^{A^m}$
are all alternative bends of
$\rho^{A^m}$
are all alternative bends of
![]() $\rho$
with Zariski dense image. Pairwise non-conjugacy of this family of Zariski dense representations also follows by an argument similar to the one given in Lemma 3·1 using Schur’s lemma, leveraging the fact that the family of bends
$\rho$
with Zariski dense image. Pairwise non-conjugacy of this family of Zariski dense representations also follows by an argument similar to the one given in Lemma 3·1 using Schur’s lemma, leveraging the fact that the family of bends
![]() $\{\rho^{A^m}\}_{m=1}^\infty$
all agree on the subgroup of the cut subsurface,
$\{\rho^{A^m}\}_{m=1}^\infty$
all agree on the subgroup of the cut subsurface,
![]() $\pi_1(S')$
, whose Zariski closure contains a principal
$\pi_1(S')$
, whose Zariski closure contains a principal
![]() $\textrm{SL}(2,\mathbf{R})$
.
$\textrm{SL}(2,\mathbf{R})$
.
Additionally, in the setting of Section 4.1, the construction works for any nonseparating simple closed curve on S, and so for each curve, different Zariski dense surface groups may be produced.
Other interesting questions in these directions still remain. For instance, one would aim to more precisely quantify how many “distinct” surface subgroups of
![]() $\textrm{SL}(n,\mathcal{O}_K)$
exist. For instance, whether or not this construction produces infinitely many commensurability classes of such subgroups considered up to conjugation is unknown. This is answered in [Reference Long and Reid17] for representations into cocompact lattices of
$\textrm{SL}(n,\mathcal{O}_K)$
exist. For instance, whether or not this construction produces infinitely many commensurability classes of such subgroups considered up to conjugation is unknown. This is answered in [Reference Long and Reid17] for representations into cocompact lattices of
![]() $\textrm{SL}(3,\mathbf{R})$
where the authors deduce the existence of an infinite family of thin surface subgroups which are pairwise non-commensurable up to conjugacy by showing the subgroups in their family have projectively distinct limit sets. For general n, the associated limit set may be studied in terms of the hyperconvex Frenet curve
$\textrm{SL}(3,\mathbf{R})$
where the authors deduce the existence of an infinite family of thin surface subgroups which are pairwise non-commensurable up to conjugacy by showing the subgroups in their family have projectively distinct limit sets. For general n, the associated limit set may be studied in terms of the hyperconvex Frenet curve
![]() $\xi_\rho\,:\,\partial_\infty\pi_1(S)\to\text{Flag}(\mathbf{R}^n)$
associated to any Hitchin representation
$\xi_\rho\,:\,\partial_\infty\pi_1(S)\to\text{Flag}(\mathbf{R}^n)$
associated to any Hitchin representation
![]() $\rho$
, first introduced in [Reference Labourie16]. It is not difficult to show that generically, the family of bends
$\rho$
, first introduced in [Reference Labourie16]. It is not difficult to show that generically, the family of bends
![]() $\{\rho^{A^m}\}_{m=1}^\infty$
produces representations whose flag curves are distinct, i.e. the functions
$\{\rho^{A^m}\}_{m=1}^\infty$
produces representations whose flag curves are distinct, i.e. the functions
![]() $\xi_{\rho^{A^j}}$
and
$\xi_{\rho^{A^j}}$
and
![]() $\xi_{\rho^{A^k}}$
are distinct whenever
$\xi_{\rho^{A^k}}$
are distinct whenever
![]() $j\neq k$
. Full non-commensurability up to conjugacy would require showing that these flag curves have distinct images, up to the action of
$j\neq k$
. Full non-commensurability up to conjugacy would require showing that these flag curves have distinct images, up to the action of
![]() $\textrm{SL}(n,\mathbf{R})$
, which remains unknown beyond the aforementioned result of [Reference Long and Reid17].
$\textrm{SL}(n,\mathbf{R})$
, which remains unknown beyond the aforementioned result of [Reference Long and Reid17].
We close with some known examples of representations this bending construction can be applied to.
-
(1) The (3,4,4)-triangle group,
 $\Delta(3,4,4)$
, is the fundamental group of the orbifold with signature
$\Delta(3,4,4)$
, is the fundamental group of the orbifold with signature
 $S^2(3,4,4)$
. Using the presentation
$S^2(3,4,4)$
. Using the presentation
 $\Delta(3,4,4)=\langle \alpha,\beta,\gamma\,|\,\alpha^3= \beta^4= \gamma^4=\alpha \beta \gamma=1\rangle$
, the representation realizing the (unique up to conjugacy) hyperbolic structure on this orbifold is given by: In [Reference Long and Thistlethwaite19] (Theorem
$\Delta(3,4,4)=\langle \alpha,\beta,\gamma\,|\,\alpha^3= \beta^4= \gamma^4=\alpha \beta \gamma=1\rangle$
, the representation realizing the (unique up to conjugacy) hyperbolic structure on this orbifold is given by: In [Reference Long and Thistlethwaite19] (Theorem \begin{align*} \rho(\alpha)&=\begin{pmatrix} 0 & -1\\1 & \phantom{-}1\end{pmatrix},\\ \rho(\beta)&=\begin{pmatrix}0 & -1-\sqrt{2}\\-1+\sqrt{2} & \sqrt{2}\end{pmatrix},\\ \rho(\gamma)&=\begin{pmatrix}1-\sqrt{2} & -\sqrt{2}\\-1+\sqrt{2} & -1\end{pmatrix}. \end{align*}
\begin{align*} \rho(\alpha)&=\begin{pmatrix} 0 & -1\\1 & \phantom{-}1\end{pmatrix},\\ \rho(\beta)&=\begin{pmatrix}0 & -1-\sqrt{2}\\-1+\sqrt{2} & \sqrt{2}\end{pmatrix},\\ \rho(\gamma)&=\begin{pmatrix}1-\sqrt{2} & -\sqrt{2}\\-1+\sqrt{2} & -1\end{pmatrix}. \end{align*}
 $2.1$
), the authors show that, when composing with the irreducible representation
$2.1$
), the authors show that, when composing with the irreducible representation
 $\tau_n\,:\,\textrm{SL}(2,\mathbf{R})\to\textrm{SL}(n,\mathbf{R})$
,
$\tau_n\,:\,\textrm{SL}(2,\mathbf{R})\to\textrm{SL}(n,\mathbf{R})$
,
 $\tau_n\rho$
can be conjugated to have image inside
$\tau_n\rho$
can be conjugated to have image inside
 $\textrm{SL}(n,\mathbf{Z})$
when n is odd, or
$\textrm{SL}(n,\mathbf{Z})$
when n is odd, or
 $\textrm{SL}(n,\mathbf{Z}[\sqrt{2}])$
when n is even (note:
$\textrm{SL}(n,\mathbf{Z}[\sqrt{2}])$
when n is even (note:
 $\mathbf{Z}[\sqrt{2}]=\mathcal{O}_{\mathbf{Q}(\sqrt{2})}$
is a PID).
$\mathbf{Z}[\sqrt{2}]=\mathcal{O}_{\mathbf{Q}(\sqrt{2})}$
is a PID).
 $\Delta(3,4,4)$
contains a torsion-free subgroup of finite-index which is the fundamental group of some closed surface:
$\Delta(3,4,4)$
contains a torsion-free subgroup of finite-index which is the fundamental group of some closed surface:
 $\pi_1(S)\leqslant\Delta(3,4,4)$
. Restricting this representation of
$\pi_1(S)\leqslant\Delta(3,4,4)$
. Restricting this representation of
 $\Delta(3,4,4)$
to one of
$\Delta(3,4,4)$
to one of
 $\pi_1(S)$
, we see that Hitchin component of S therefore contains a
$\pi_1(S)$
, we see that Hitchin component of S therefore contains a
 $\mathbf{Z}$
-point or a
$\mathbf{Z}$
-point or a
 $\mathbf{Z}[\sqrt{2}]$
-point depending on the parity of n, and so can be bent to being Zariski dense.
$\mathbf{Z}[\sqrt{2}]$
-point depending on the parity of n, and so can be bent to being Zariski dense. -
(2) More generally, for
 $\Gamma\lt\textrm{SL}(2,\mathbf{R})$
a cocompact arithmetic Fuchsian group,
$\Gamma\lt\textrm{SL}(2,\mathbf{R})$
a cocompact arithmetic Fuchsian group,
 $\Gamma\lt\textrm{SL}(2,\mathcal{O}_K)$
for some number field K. When K is totally real and has class number one, we may run the above construction on a torsion-free subgroup of
$\Gamma\lt\textrm{SL}(2,\mathcal{O}_K)$
for some number field K. When K is totally real and has class number one, we may run the above construction on a torsion-free subgroup of
 $\tau_n(\Gamma) \lt \textrm{SL}(n,\mathcal{O}_K)$
to produce Zariski dense surface subgroups of other groups (note: the irreducible embedding,
$\tau_n(\Gamma) \lt \textrm{SL}(n,\mathcal{O}_K)$
to produce Zariski dense surface subgroups of other groups (note: the irreducible embedding,
 $\tau_n$
, can be defined over
$\tau_n$
, can be defined over
 $\mathbf{Z}$
, hence takes
$\mathbf{Z}$
, hence takes
 $\textrm{SL}(2,\mathcal{O}_K)$
into
$\textrm{SL}(2,\mathcal{O}_K)$
into
 $\textrm{SL}(n,\mathcal{O}_K)$
). See, for instance, [Reference Morris22, example 6·3·2] for constructions of arithmetic Fuchsian subgroups of
$\textrm{SL}(n,\mathcal{O}_K)$
). See, for instance, [Reference Morris22, example 6·3·2] for constructions of arithmetic Fuchsian subgroups of
 $\textrm{SL}(2,\mathcal{O}_K)$
various totally real K aside from
$\textrm{SL}(2,\mathcal{O}_K)$
various totally real K aside from
 $\mathbf{Q}(\sqrt{2})$
.
$\mathbf{Q}(\sqrt{2})$
. -
(3) Examples of
 $\mathbf{Q}$
-integral even-dimensional Hitchin representations are largely unknown. At the moment of writing, such examples are only known when
$\mathbf{Q}$
-integral even-dimensional Hitchin representations are largely unknown. At the moment of writing, such examples are only known when
 $n=4$
. Long and Thistlethwaite provided such examples of Hitchin representations into
$n=4$
. Long and Thistlethwaite provided such examples of Hitchin representations into
 $\textrm{SL}(4,\mathbf{Z})$
in [Reference Long and Thistlethwaite18]: one coming from an infinite family of representations of the triangle group
$\textrm{SL}(4,\mathbf{Z})$
in [Reference Long and Thistlethwaite18]: one coming from an infinite family of representations of the triangle group
 $\Delta(3,3,4)$
, along with one of the triangle group
$\Delta(3,3,4)$
, along with one of the triangle group
 $\Delta(2,4,5)$
. These methods then provide an alternate proof of the results of the aforementioned paper, giving Zariski dense surface subgroups in
$\Delta(2,4,5)$
. These methods then provide an alternate proof of the results of the aforementioned paper, giving Zariski dense surface subgroups in
 $\textrm{SL}(4,\mathbf{Z})$
, but additional examples for
$\textrm{SL}(4,\mathbf{Z})$
, but additional examples for
 $\textrm{SL}(2k,\mathbf{Z})$
when
$\textrm{SL}(2k,\mathbf{Z})$
when
 $k\gt2$
are still unknown.
$k\gt2$
are still unknown.
Acknowledgements
The author would like to thank Darren Long for the guidance provided throughout the writing of this paper. In particular, his numerous helpful discussions held with the author and comments on early drafts were instrumental in the completion of this work. The author also thanks the anonymous referee for many helpful comments.