1. Introduction
1·1. Dirichlet L-series at
 $s = 0$
and annihilation of class groups
$s = 0$
and annihilation of class groups
Stark’s conjecture predicts a description for the leading term of a general Artin L-series at
![]() $s = 0$
up to an unspecified rational factor. Formulating an integral refinement of this conjecture turned out to be a delicate task that Stark himself, in [
Reference Stark54
], only found a solution to in the case that the order of vanishing of the L-series at
$s = 0$
up to an unspecified rational factor. Formulating an integral refinement of this conjecture turned out to be a delicate task that Stark himself, in [
Reference Stark54
], only found a solution to in the case that the order of vanishing of the L-series at
![]() $s = 0$
is one. Initial generalisations to higher orders of vanishing, for example the ‘question’ of Stark in [
Reference Grant29
,
Reference Tangedal55
] or a conjecture of Sands [
Reference Sands50
, Conjecture 2·0], were subsequently shown to not hold in general by Rubin [
Reference Rubin48
, Section 4] and Popescu [
Reference Popescu47
]. Instead, Rubin proposed in loc. cit. what is now commonly referred to as the ‘Rubin–Stark conjecture’.
$s = 0$
is one. Initial generalisations to higher orders of vanishing, for example the ‘question’ of Stark in [
Reference Grant29
,
Reference Tangedal55
] or a conjecture of Sands [
Reference Sands50
, Conjecture 2·0], were subsequently shown to not hold in general by Rubin [
Reference Rubin48
, Section 4] and Popescu [
Reference Popescu47
]. Instead, Rubin proposed in loc. cit. what is now commonly referred to as the ‘Rubin–Stark conjecture’.
Going beyond mere integrality, it is expected that this unspecified factor encodes important arithmetic information and, in particular, is linked to the Galois module structure of class groups. The primordial example of this phenomenon is Stickelberger’s theorem from the 19th century, which asserts that the ideal class group of a cyclotomic field is annihilated by a certain element valued in the group ring over the relevant Galois group and constructed from values of Dirichlet L-series at
![]() $s = 0$
. The analogous annihilation statement for class groups of finite abelian CM extensions of totally real fields is known as the ‘Brumer–Stark conjecture’ and has very recently been settled by Dasgupta and Kakde [
Reference Dasgupta and Kakde21
] with additional arguments by Dasgupta, Kakde, Silliman and Wang [
Reference Dasgupta, Kakde, Silliman and Wang23
]. In certain situations, these results can even be extended to non-abelian CM extensions, see [
Reference Burns and Johnston16
,
Reference Ellerbrock and Nickel26
,
Reference Johnston and Nickel33
].
$s = 0$
. The analogous annihilation statement for class groups of finite abelian CM extensions of totally real fields is known as the ‘Brumer–Stark conjecture’ and has very recently been settled by Dasgupta and Kakde [
Reference Dasgupta and Kakde21
] with additional arguments by Dasgupta, Kakde, Silliman and Wang [
Reference Dasgupta, Kakde, Silliman and Wang23
]. In certain situations, these results can even be extended to non-abelian CM extensions, see [
Reference Burns and Johnston16
,
Reference Ellerbrock and Nickel26
,
Reference Johnston and Nickel33
].
However, outside the setting of totally imaginary extensions of totally real fields the values of the associated Dirichlet L-series at
![]() $s = 0$
usually vanish (the only exception being the case considered by Nomura in [
Reference Nomura45
]) and so naive generalisations of Stickelberger’s theorem become trivial. This led Burns to formulate the question whether in such cases one can instead use higher derivatives of Dirichlet L-series to produce annihilators of class groups (see [
Reference Macías Castillo37
, Question 1·1]) and similar aspects have also been considered by Buckingham [
Reference Buckingham7
,
Reference Buckingham8
].
$s = 0$
usually vanish (the only exception being the case considered by Nomura in [
Reference Nomura45
]) and so naive generalisations of Stickelberger’s theorem become trivial. This led Burns to formulate the question whether in such cases one can instead use higher derivatives of Dirichlet L-series to produce annihilators of class groups (see [
Reference Macías Castillo37
, Question 1·1]) and similar aspects have also been considered by Buckingham [
Reference Buckingham7
,
Reference Buckingham8
].
In this article, we prove new results on the Rubin–Stark conjecture and, moreover, on the annihilation of class groups, in cases of higher orders of vanishing. Indeed, in Theorem 1·1 we extend annihilation results concerning multi-quadratic extensions by Sands [
Reference Sands52
] and the second author [
Reference Macías Castillo37
] to general p-elementary abelian extensions
![]() $K/k$
of number fields, for arbitrary prime numbers p. This result is conditional on the collection of subextensions
$K/k$
of number fields, for arbitrary prime numbers p. This result is conditional on the collection of subextensions
![]() $L/k$
of
$L/k$
of
![]() $K/k$
that have degree p validating a conjecture of Burns, Kurihara and Sano (which we recall as Conjecture 1·10). Since we are then also able, in Theorem 1·3, to prove new cases of the Burns–Kurihara–Sano conjecture, we derive a method of systematically producing examples in which the annihilation claim of Theorem 1·1 is valid unconditionally (see Corollary 1·8).
$K/k$
that have degree p validating a conjecture of Burns, Kurihara and Sano (which we recall as Conjecture 1·10). Since we are then also able, in Theorem 1·3, to prove new cases of the Burns–Kurihara–Sano conjecture, we derive a method of systematically producing examples in which the annihilation claim of Theorem 1·1 is valid unconditionally (see Corollary 1·8).
1·2. Statements of the main results
To describe our results in more detail, we fix a finite abelian extension of number fields
![]() $K / k$
with Galois group
$K / k$
with Galois group
![]() $G \,{:\!=}\, \mathrm{Gal}({K}/{k})$
and, following Rubin [
Reference Rubin48
, Hypothesis 2·1], a triple (S, V, T) of finite sets of places of k with the following properties:
$G \,{:\!=}\, \mathrm{Gal}({K}/{k})$
and, following Rubin [
Reference Rubin48
, Hypothesis 2·1], a triple (S, V, T) of finite sets of places of k with the following properties:
-
(H1) S contains both the set
 $S_\infty$
of infinite places of k and the places that ramify in K;
$S_\infty$
of infinite places of k and the places that ramify in K; -
(H2)
 $V \subsetneq S$
is a proper subset comprising places which split completely in
$V \subsetneq S$
is a proper subset comprising places which split completely in
 $K / k$
;
$K / k$
; -
(H3) T is disjoint from S and such that the group
 $\mathcal{O}^\times_{K, S, T} \,{:\!=}\, \{ a \in K^\times \mid {\mathrm{ord}}_w (a) = 0 \text{ if } w \not \in S_K, {\mathrm{ord}}_w (a - 1) \gt 0 \text{ if } w \in T_K \}$
is
$\mathcal{O}^\times_{K, S, T} \,{:\!=}\, \{ a \in K^\times \mid {\mathrm{ord}}_w (a) = 0 \text{ if } w \not \in S_K, {\mathrm{ord}}_w (a - 1) \gt 0 \text{ if } w \in T_K \}$
is
 ${\mathbb{Z}}$
-torsion free. (Here
${\mathbb{Z}}$
-torsion free. (Here
 $S_K$
and
$S_K$
and
 $T_K$
denote the sets of places of K that lie above those in S and T, respectively, and
$T_K$
denote the sets of places of K that lie above those in S and T, respectively, and
 ${\mathrm{ord}}_w$
is the normalised valuation attached to w.)
${\mathrm{ord}}_w$
is the normalised valuation attached to w.)
We refer to such a triple (S, V, T) as a ‘Rubin datum’ for
![]() $K / k$
. For any Rubin datum and character
$K / k$
. For any Rubin datum and character
![]() $\chi$
in
$\chi$
in
![]() $\widehat{G} \,{:\!=}\, \mathrm{Hom}_{\mathbb{Z}} (G, {\mathbb{C}}^\times)$
, the (S-truncated, T-modified) Dirichlet L-series
$\widehat{G} \,{:\!=}\, \mathrm{Hom}_{\mathbb{Z}} (G, {\mathbb{C}}^\times)$
, the (S-truncated, T-modified) Dirichlet L-series
is known to admit a meromorphic continuation to
![]() ${\mathbb{C}}$
that is holomorphic and of order of vanishing at least
${\mathbb{C}}$
that is holomorphic and of order of vanishing at least
![]() $|V|$
at
$|V|$
at
![]() $s = 0$
(cf. [
Reference Tate56
, Chapter I, Proposition 3·4]). We may therefore define the (
$s = 0$
(cf. [
Reference Tate56
, Chapter I, Proposition 3·4]). We may therefore define the (
![]() $|V|$
-th order) ‘Stickelberger element’
$|V|$
-th order) ‘Stickelberger element’
with
![]() $e_\chi \,{:\!=}\, |G|^{-1} \sum_{\sigma \in G} \chi (\sigma)^{-1} \sigma$
the usual primitive orthogonal idempotent in
$e_\chi \,{:\!=}\, |G|^{-1} \sum_{\sigma \in G} \chi (\sigma)^{-1} \sigma$
the usual primitive orthogonal idempotent in
![]() ${\mathbb{C}} [G]$
associated with
${\mathbb{C}} [G]$
associated with
![]() $\chi$
. In addition, we define
$\chi$
. In addition, we define
![]() $X_{K, S} \subseteq Y_{K, S} \,{:\!=}\, \bigoplus_{w \in S_K} {\mathbb{Z}} w$
to be the
$X_{K, S} \subseteq Y_{K, S} \,{:\!=}\, \bigoplus_{w \in S_K} {\mathbb{Z}} w$
to be the
![]() ${\mathbb{Z}} [G]$
-submodule of elements whose coefficients sum to zero, and denote the Dirichlet regulator isomorphism by
${\mathbb{Z}} [G]$
-submodule of elements whose coefficients sum to zero, and denote the Dirichlet regulator isomorphism by
The Rubin–Stark conjecture [
Reference Rubin48
, Conjecture B’] now predicts, via the reinterpretation given in Lemma 2·2 below, that for every homomorphism of
![]() $\mathbb{Z}[G]$
-modules
$\mathbb{Z}[G]$
-modules
![]() $f {\colon} \mathcal{O}_{K, S, T}^\times \to X_{K, S}$
one has
$f {\colon} \mathcal{O}_{K, S, T}^\times \to X_{K, S}$
one has
with
![]() $f_\mathbb{R}$
the scalar extension
$f_\mathbb{R}$
the scalar extension
![]() ${\mathbb{R}}\otimes_{\mathbb{Z}} f{\colon}{\mathbb{R}} \otimes_{\mathbb{Z}} \mathcal{O}_{K, S}^\times={\mathbb{R}} \otimes_{\mathbb{Z}} \mathcal{O}_{K, S,T}^\times\longrightarrow\mathbb{R}\otimes_\mathbb{Z} X_{K,S}$
of f. In addition, it is expected that the element in (1·2) annihilates the
${\mathbb{R}}\otimes_{\mathbb{Z}} f{\colon}{\mathbb{R}} \otimes_{\mathbb{Z}} \mathcal{O}_{K, S}^\times={\mathbb{R}} \otimes_{\mathbb{Z}} \mathcal{O}_{K, S,T}^\times\longrightarrow\mathbb{R}\otimes_\mathbb{Z} X_{K,S}$
of f. In addition, it is expected that the element in (1·2) annihilates the
![]() $S_K$
-class group of K (cf. [
Reference Burns13
, Conjecture 2·4·1] or [
Reference Macías Castillo37
, Question 1·1]). Here we study a refinement of this question that instead considers the
$S_K$
-class group of K (cf. [
Reference Burns13
, Conjecture 2·4·1] or [
Reference Macías Castillo37
, Question 1·1]). Here we study a refinement of this question that instead considers the
![]() $S_K$
-ray class group
$S_K$
-ray class group
![]() ${\mathrm{Cl}}_{K, S, T}$
of K mod
${\mathrm{Cl}}_{K, S, T}$
of K mod
![]() $T_K$
(defined as the quotient of the group of fractional ideals of
$T_K$
(defined as the quotient of the group of fractional ideals of
![]() ${\mathcal{O}}_{K, S}$
coprime to
${\mathcal{O}}_{K, S}$
coprime to
![]() $T_K$
, by the subgroup of principal ideals with a generator congruent to 1 modulo all
$T_K$
, by the subgroup of principal ideals with a generator congruent to 1 modulo all
![]() $w \in T_K$
).
$w \in T_K$
).
To state our first main result in this direction we fix a prime number p, consider a p-elementary abelian extension
![]() $K/k$
and write
$K/k$
and write
![]() $\Omega$
for the set of degree-p subextensions
$\Omega$
for the set of degree-p subextensions
![]() $L/k$
of
$L/k$
of
![]() $K/k$
.
$K/k$
.
Theorem 1·1. Let
![]() $K / k$
be a p-elementary abelian extension of number fields of degree
$K / k$
be a p-elementary abelian extension of number fields of degree
![]() $p^m$
and fix a Rubin datum (S, V, T) for
$p^m$
and fix a Rubin datum (S, V, T) for
![]() $K / k$
that satisfies
$K / k$
that satisfies
where
![]() $s_p \,{:\!=}\, \dim_{\mathbb{F}_p} ({\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p)$
denotes the p-rank of the S-ray class group mod T of k.
$s_p \,{:\!=}\, \dim_{\mathbb{F}_p} ({\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p)$
denotes the p-rank of the S-ray class group mod T of k.
If for all subextensions
![]() $L / k$
in
$L / k$
in
![]() $\Omega$
the Burns–Kurihara–Sano conjecture [
Reference Burns, Kurihara and Sano17
, Conjecture 7·3] is valid for
$\Omega$
the Burns–Kurihara–Sano conjecture [
Reference Burns, Kurihara and Sano17
, Conjecture 7·3] is valid for
![]() $(L/k,S,V,T)$
, then
$(L/k,S,V,T)$
, then
In particular, the Rubin–Stark conjecture is valid for
![]() $(K/k,S,V,T)$
.
$(K/k,S,V,T)$
.
Remark 1·2. If
![]() $p = 2$
, then each subextension in
$p = 2$
, then each subextension in
![]() $\Omega$
is quadratic and Theorem 1·1 is unconditional (see Remark 1·11 (d)) and recovers results of Sands [
Reference Sands51
, Theorem 2·2] on the Rubin–Stark conjecture and of Sands [
Reference Sands52
, Main theorem] and the second author [
Reference Macías Castillo37
, Theorem 1·4] on the annihilation of class groups.
$\Omega$
is quadratic and Theorem 1·1 is unconditional (see Remark 1·11 (d)) and recovers results of Sands [
Reference Sands51
, Theorem 2·2] on the Rubin–Stark conjecture and of Sands [
Reference Sands52
, Main theorem] and the second author [
Reference Macías Castillo37
, Theorem 1·4] on the annihilation of class groups.
To prove Theorem 1·1 (in Section 4) we first deduce in Lemma 4·2 the validity of the Rubin–Stark conjecture for
![]() $K / k$
from the assumed validity of conjecture [
Reference Burns, Kurihara and Sano17
, Conjecture 7·3] for all subextensions in
$K / k$
from the assumed validity of conjecture [
Reference Burns, Kurihara and Sano17
, Conjecture 7·3] for all subextensions in
![]() $\Omega$
. The annihilation statement in Theorem 1·1 is then deduced from this by varying the Rubin datum in combination with Cebotarev’s density theorem, as in the theory of ‘Stark systems’ (see, for example, [
Reference Burns, Sakamoto and Sano18
, Section 4]). Although this latter aspect of the argument is of a general nature, we prefer to focus on the concrete situation of Theorem 1·1 in this article and to discuss the general formalism elsewhere.
$\Omega$
. The annihilation statement in Theorem 1·1 is then deduced from this by varying the Rubin datum in combination with Cebotarev’s density theorem, as in the theory of ‘Stark systems’ (see, for example, [
Reference Burns, Sakamoto and Sano18
, Section 4]). Although this latter aspect of the argument is of a general nature, we prefer to focus on the concrete situation of Theorem 1·1 in this article and to discuss the general formalism elsewhere.
As our second main result, we prove new cases of the Burns–Kurihara–Sano conjecture.
Theorem 1·3. Let
![]() $K / k$
be an extension of number fields of one of the following forms:
$K / k$
be an extension of number fields of one of the following forms:
-
(i) There exists a prime-power q and a subfield
 $\kappa$
of k such that
$\kappa$
of k such that
 $K / \kappa$
is a Galois extension with Galois group isomorphic to the group
$K / \kappa$
is a Galois extension with Galois group isomorphic to the group
 ${\mathrm{Aff}} (q)$
of affine transformations of the field
${\mathrm{Aff}} (q)$
of affine transformations of the field
 $\mathbb{F}_q$
with q elements, and
$\mathbb{F}_q$
with q elements, and
 $G = \mathrm{Gal}({K}/{k})$
is the unique subgroup of order q of
$G = \mathrm{Gal}({K}/{k})$
is the unique subgroup of order q of
 $\mathrm{Gal}({K}/{\kappa})$
.
$\mathrm{Gal}({K}/{\kappa})$
. -
(ii)
 $K / k$
is a biquadratic extension.
$K / k$
is a biquadratic extension.
Then, given any Rubin datum (S, V, T) for
![]() $K / k$
that satisfies
$K / k$
that satisfies
![]() $|S| \gt |V| + 1$
, the Burns–Kurihara–Sano conjecture is valid for
$|S| \gt |V| + 1$
, the Burns–Kurihara–Sano conjecture is valid for
![]() $(K/k,S,V,T)$
. In particular, the Rubin–Stark conjecture is also valid for
$(K/k,S,V,T)$
. In particular, the Rubin–Stark conjecture is also valid for
![]() $(K/k,S,V,T)$
.
$(K/k,S,V,T)$
.
Remark 1·4. The condition
![]() $|S| \gt |V| + 1$
often already follows from (H1) and (H2). For example, if k has odd class number, then class field theory implies that there can only be finitely many biquadratic extensions K of k that admit a Rubin datum (S, V, T) with
$|S| \gt |V| + 1$
often already follows from (H1) and (H2). For example, if k has odd class number, then class field theory implies that there can only be finitely many biquadratic extensions K of k that admit a Rubin datum (S, V, T) with
![]() $|S| = |V| + 1$
.
$|S| = |V| + 1$
.
Example 1·5. Fix a prime number p and let
![]() $\zeta_p$
be a primitive pth root of unity in an algebraic closure of
$\zeta_p$
be a primitive pth root of unity in an algebraic closure of
![]() ${\mathbb{Q}}$
. Let
${\mathbb{Q}}$
. Let
![]() $\kappa$
be a number field with the property that
$\kappa$
be a number field with the property that
![]() $\kappa \cap {\mathbb{Q}} (\zeta_p) = {\mathbb{Q}}$
. If we pick any element
$\kappa \cap {\mathbb{Q}} (\zeta_p) = {\mathbb{Q}}$
. If we pick any element
![]() $a \in \kappa^\times$
that is not a pth power in
$a \in \kappa^\times$
that is not a pth power in
![]() $\kappa$
, then it is also not a pth power in
$\kappa$
, then it is also not a pth power in
![]() $k \,{:\!=}\, \kappa (\zeta_p)$
and
$k \,{:\!=}\, \kappa (\zeta_p)$
and
![]() $K \,{:\!=}\, k ( \sqrt[p]{a})$
is an extension of the form (i) with
$K \,{:\!=}\, k ( \sqrt[p]{a})$
is an extension of the form (i) with
![]() $q = p$
.
$q = p$
.
Remark 1·6. The Burns–Kurihara–Sano conjecture (for arbitrary Rubin datum) is known to be a consequence of the ‘equivariant Tamagawa Number Conjecture’ (eTNC) for
![]() $K / k$
by [
Reference Burns, Kurihara and Sano17
, Theorem 7·5]. (Note that the eTNC is referred to as the ‘Leading Term Conjecture’ LTC
$K / k$
by [
Reference Burns, Kurihara and Sano17
, Theorem 7·5]. (Note that the eTNC is referred to as the ‘Leading Term Conjecture’ LTC
![]() $(K/k)$
in the cited result, cf. [
Reference Burns, Kurihara and Sano17
, Proposition 3·4 and Remark 3·2]) For the extensions
$(K/k)$
in the cited result, cf. [
Reference Burns, Kurihara and Sano17
, Proposition 3·4 and Remark 3·2]) For the extensions
![]() $K / k$
considered in Theorem 1·3 and any prime
$K / k$
considered in Theorem 1·3 and any prime
![]() $\ell$
not dividing
$\ell$
not dividing
![]() $[K : k]$
, the ‘
$[K : k]$
, the ‘
![]() $\ell$
-component’ of
$\ell$
-component’ of
![]() $\mathrm{eTNC}(K/k)$
can easily be seen to follow from the analytic class number formula (via Tate’s proof [
Reference Tate56
, Chapter II, Theorem 6·8] of the ‘strong Stark conjecture’ in this setting) and Johnston and Nickel have proved in [
Reference Johnston and Nickel32
, Theorem 4·6] that in certain instances of case (i) one can even deduce the
$\mathrm{eTNC}(K/k)$
can easily be seen to follow from the analytic class number formula (via Tate’s proof [
Reference Tate56
, Chapter II, Theorem 6·8] of the ‘strong Stark conjecture’ in this setting) and Johnston and Nickel have proved in [
Reference Johnston and Nickel32
, Theorem 4·6] that in certain instances of case (i) one can even deduce the
![]() $\ell$
-component of
$\ell$
-component of
![]() $\mathrm{eTNC}(K/\kappa)$
. Of most interest, therefore, is the component of
$\mathrm{eTNC}(K/\kappa)$
. Of most interest, therefore, is the component of
![]() $\mathrm{eTNC}(K/k)$
at the unique prime dividing
$\mathrm{eTNC}(K/k)$
at the unique prime dividing
![]() $[K : k]$
.
$[K : k]$
.
However, a proof of this component seems to be out of reach at present since even in the case (ii) of biquadratic extensions it amounts to a difficult, yet explicit, question regarding signs (see Remark 3·2 for more details). The perhaps surprising insight behind the proof of Theorem 1·3 is that the information provided by the analytic class number formula is nevertheless sufficient to allow for the deduction of the Burns–Kurihara–Sano conjecture, subject only to the restriction that
![]() $|S| \gt |V| + 1$
. In fact, the direct argument given in Section 3·1 is uniform and does not require a distinction between
$|S| \gt |V| + 1$
. In fact, the direct argument given in Section 3·1 is uniform and does not require a distinction between
![]() $\ell\nmid[K : k]$
and
$\ell\nmid[K : k]$
and
![]() $\ell\mid[K : k]$
.
$\ell\mid[K : k]$
.
Remark 1·7. Johnston and Nickel [
Reference Johnston and Nickel32
, Theorem 7·6] have also proved a conjecture of Burns (from [
Reference Burns13
]) regarding the annihilation of class groups in extensions
![]() $K / \kappa$
as in case (i) for which
$K / \kappa$
as in case (i) for which
![]() $k / {\mathbb{Q}}$
is abelian.
$k / {\mathbb{Q}}$
is abelian.
Results on the Rubin–Stark conjecture in the literature outside the classical cases where at most one archimedean place of k splits in K or the degree
![]() $[K : k]$
is at most two are sparse (see Remark 1·11 for a list of known cases). By combining Theorems 1·3 and 1·1 with Example 1·5, we now obtain the following method to systematically produce new examples in which the conjecture is valid.
$[K : k]$
is at most two are sparse (see Remark 1·11 for a list of known cases). By combining Theorems 1·3 and 1·1 with Example 1·5, we now obtain the following method to systematically produce new examples in which the conjecture is valid.
Corollary 1·8. Let p be a prime number, let
![]() $\zeta_p$
be a primitive
$\zeta_p$
be a primitive
![]() $p$
-th root of unity, and let
$p$
-th root of unity, and let
![]() $\kappa$
be a number field with the property that
$\kappa$
be a number field with the property that
![]() $\kappa \cap {\mathbb{Q}} (\mu_p) = {\mathbb{Q}}$
. Let
$\kappa \cap {\mathbb{Q}} (\mu_p) = {\mathbb{Q}}$
. Let
![]() $a_1, \dots, a_m$
be elements of
$a_1, \dots, a_m$
be elements of
![]() $\kappa$
that are
$\kappa$
that are
![]() $\mathbb{F}_p$
-linearly independent in
$\mathbb{F}_p$
-linearly independent in
![]() $\kappa^\times / (\kappa^\times)^p$
, and set
$\kappa^\times / (\kappa^\times)^p$
, and set
![]() $k \,{:\!=}\, \kappa (\mu_p)$
and
$k \,{:\!=}\, \kappa (\mu_p)$
and
![]() $K \,{:\!=}\, k (\sqrt[p]{a_1}, \dots, \sqrt[p]{a_m})$
.
$K \,{:\!=}\, k (\sqrt[p]{a_1}, \dots, \sqrt[p]{a_m})$
.
If (S, V, T) is a Rubin datum for
![]() $K / k$
with
$K / k$
with
then
In particular, the Rubin–Stark conjecture is valid for
![]() $(K/k,S,V,T)$
.
$(K/k,S,V,T)$
.
Proof. The kernel of the natural map
![]() $\kappa^\times / (\kappa^\times)^p \to k^\times / (k^\times)^p$
identifies with
$\kappa^\times / (\kappa^\times)^p \to k^\times / (k^\times)^p$
identifies with
![]() $H^1 (\mathrm{Gal}({k}/{\kappa}), \mu_p)$
, and hence vanishes. It follows that
$H^1 (\mathrm{Gal}({k}/{\kappa}), \mu_p)$
, and hence vanishes. It follows that
![]() $a_1, \dots, a_m$
generate an
$a_1, \dots, a_m$
generate an
![]() $\mathbb{F}_p$
-subvectorspace of
$\mathbb{F}_p$
-subvectorspace of
![]() $k^\times / (k^\times)^p$
of dimension m. By Kummer theory, one therefore has that
$k^\times / (k^\times)^p$
of dimension m. By Kummer theory, one therefore has that
![]() $[K : k] = p^m$
and so, noting that
$[K : k] = p^m$
and so, noting that
![]() $\mathrm{Gal}({k (\sqrt[p]{a_i})}/{\kappa}) \cong \mathrm{Aff}(p)$
for every
$\mathrm{Gal}({k (\sqrt[p]{a_i})}/{\kappa}) \cong \mathrm{Aff}(p)$
for every
![]() $i \in \{1, \dots, m \}$
because
$i \in \{1, \dots, m \}$
because
![]() $\kappa \cap {\mathbb{Q}} (\mu_p) = {\mathbb{Q}}$
, the result follows by combining Theorems 1·3 and 1·1.
$\kappa \cap {\mathbb{Q}} (\mu_p) = {\mathbb{Q}}$
, the result follows by combining Theorems 1·3 and 1·1.
1·3. The conjectures of Rubin–Stark and Burns–Kurihara–Sano
In this section we state the Rubin–Stark conjecture and the conjecture [ Reference Burns, Kurihara and Sano17 , Conjecture 7·3] of Burns, Kurihara and Sano, and we discuss the list of cases in which either conjecture is known to be valid. The formulations given here, in terms of the products of the form (1·2), are equivalent to the original versions of the conjectures by Lemma 2·2 below.
We fix a finite abelian extension of number fields
![]() $K/k$
with Galois group
$K/k$
with Galois group
![]() $G \,{:\!=}\, \mathrm{Gal}({K}/{k})$
and Rubin datum (S,V,T).
$G \,{:\!=}\, \mathrm{Gal}({K}/{k})$
and Rubin datum (S,V,T).
Conjecture 1·9 (Rubin–Stark, [ Reference Rubin48 , Conjecture B’]). One has
We set
![]() $K_T^\times \,{:\!=}\, \{ a \in K^\times \mid {\mathrm{ord}}_w (a - 1) \gt 0 \text{ if } w \in T_K\}$
. Then the ‘integral dual Selmer group’
$K_T^\times \,{:\!=}\, \{ a \in K^\times \mid {\mathrm{ord}}_w (a - 1) \gt 0 \text{ if } w \in T_K\}$
. Then the ‘integral dual Selmer group’
![]() $\mathrm{Sel}_{K, S, T}$
is defined by Burns–Kurihara–Sano [
Reference Burns, Kurihara and Sano17
, Definition 2·1] as the cokernel of the map
$\mathrm{Sel}_{K, S, T}$
is defined by Burns–Kurihara–Sano [
Reference Burns, Kurihara and Sano17
, Definition 2·1] as the cokernel of the map
It fits into a canonical exact sequence of G-modules
with all duals endowed with the contragredient G-action.
In the sequel, for
![]() $n\geq 0$
, we write
$n\geq 0$
, we write
![]() ${\operatorname{Fitt}}^n_{{\mathbb{Z}} [G]} (M)$
for the
${\operatorname{Fitt}}^n_{{\mathbb{Z}} [G]} (M)$
for the
![]() $n$
-
th Fitting ideal in
$n$
-
th Fitting ideal in
![]() $\mathbb{Z}[G]$
of a finitely presented
$\mathbb{Z}[G]$
of a finitely presented
![]() ${\mathbb{Z}} [G]$
-module M (see, for example, [
Reference Northcott46
, Section 3·1] or [
Reference Nickel43
]). Given a subset I of
${\mathbb{Z}} [G]$
-module M (see, for example, [
Reference Northcott46
, Section 3·1] or [
Reference Nickel43
]). Given a subset I of
![]() ${\mathbb{C}} [G]$
, we denote by
${\mathbb{C}} [G]$
, we denote by
![]() $I^\#$
the image of I under the involution of
$I^\#$
the image of I under the involution of
![]() ${\mathbb{C}} [G]$
that inverts elements of G.
${\mathbb{C}} [G]$
that inverts elements of G.
Burns–Kurihara–Sano use the Selmer group to refine Conjecture 1·9 as follows.
Conjecture 1·10 (Burns–Kurihara–Sano [ Reference Burns, Kurihara and Sano17 , Conjecture 7·3]). One has
Remark 1·11. To the best of the authors’ knowledge, the following is a complete list of cases in which the Rubin–Stark conjecture is known at present.
-
(a) One can directly verify the conjecture for the following general classes of extensions
 $K / k$
:
$K / k$
:-
(i) if
 $[K\,{:}\,k] \leq 2$
, then it follows from the analytic class number formula (see [
Reference Rubin48
, Corollary 3·2 and Theorem 3·5]);
$[K\,{:}\,k] \leq 2$
, then it follows from the analytic class number formula (see [
Reference Rubin48
, Corollary 3·2 and Theorem 3·5]); -
(ii) if
 $k = {\mathbb{Q}}$
and
$k = {\mathbb{Q}}$
and
 $V = S_\infty$
is the singleton comprising the unique infinite place of
$V = S_\infty$
is the singleton comprising the unique infinite place of
 ${\mathbb{Q}}$
, then it follows by means of a direct computation that shows that the relevant Rubin–Stark element (as defined in section 2·1) can be expressed in terms of a cyclotomic unit (cf. [
Reference Tate56
, Chapter III, Section 5]);
${\mathbb{Q}}$
, then it follows by means of a direct computation that shows that the relevant Rubin–Stark element (as defined in section 2·1) can be expressed in terms of a cyclotomic unit (cf. [
Reference Tate56
, Chapter III, Section 5]); -
(iii) if k is an imaginary quadratic field and
 $V = S_\infty$
is the singleton comprising the unique infinite place of k, then it follows from Kronecker’s Second Limit Formula for elliptic units (cf. [
Reference Tate56
, Chapter IV, Proposition 3·9]);
$V = S_\infty$
is the singleton comprising the unique infinite place of k, then it follows from Kronecker’s Second Limit Formula for elliptic units (cf. [
Reference Tate56
, Chapter IV, Proposition 3·9]); -
(iv) if
 $V = {\varnothing}$
, then it is a consequence of work of Cassou-Noguès [
Reference Cassou-Noguès19
] and, independently, Deligne and Ribet [
Reference Deligne and Ribet24
] (cf. [
Reference Gross30
, Proposition 3·7]).
$V = {\varnothing}$
, then it is a consequence of work of Cassou-Noguès [
Reference Cassou-Noguès19
] and, independently, Deligne and Ribet [
Reference Deligne and Ribet24
] (cf. [
Reference Gross30
, Proposition 3·7]).
-
-
(b) In addition, the conjecture has been directly verified in the following particular cases.
-
(i) Grant [ Reference Grant29 ] has verified it for
 $k = {\mathbb{Q}} ( \zeta_5)$
and
$k = {\mathbb{Q}} ( \zeta_5)$
and
 $K = k ( \sqrt[5]{\epsilon})$
with
$K = k ( \sqrt[5]{\epsilon})$
with
 $\zeta$
a primitive 5th root of unity and
$\zeta$
a primitive 5th root of unity and
 $\epsilon \,{:\!=}\, - \zeta^2 - \zeta^3$
.
$\epsilon \,{:\!=}\, - \zeta^2 - \zeta^3$
. -
(ii) If
 $K / k$
is multi-quadratic, then Dummit, Sands and Tangedal [
Reference Dummit, Sands and Tangedal25
], Sands [
Reference Sands51
], and the second author [
Reference Macías Castillo37
] have verified it in special cases.
$K / k$
is multi-quadratic, then Dummit, Sands and Tangedal [
Reference Dummit, Sands and Tangedal25
], Sands [
Reference Sands51
], and the second author [
Reference Macías Castillo37
] have verified it in special cases. -
(iii) McGown, Sands and Vallières [ Reference McGown, Sands and Vallières38 ] have numerically verified it for
 $V = S_\infty$
in the 19197 examples of k a real quadratic field and K a totally real cubic extensions of k of discriminant less than
$V = S_\infty$
in the 19197 examples of k a real quadratic field and K a totally real cubic extensions of k of discriminant less than
 $10^{12}$
and
$10^{12}$
and
 $V = S_\infty$
$V = S_\infty$
-
-
(c) It holds if
 $S \setminus V$
contains a place that splits completely in K (cf. [
Reference Rubin48
, Proposition 3·1]).
$S \setminus V$
contains a place that splits completely in K (cf. [
Reference Rubin48
, Proposition 3·1]). -
(d) The examples listed in (a) are by now sufficiently well understood to allow for a proof of
 $\mathrm{eTNC}(K/k)$
[
Reference Burns, Kurihara and Sano17
, Conjecture 3·6]. By [
Reference Burns, Kurihara and Sano17
, Theorem 7·5], for any given Rubin datum for
$\mathrm{eTNC}(K/k)$
[
Reference Burns, Kurihara and Sano17
, Conjecture 3·6]. By [
Reference Burns, Kurihara and Sano17
, Theorem 7·5], for any given Rubin datum for
 $K/k$
, the conjecture [
Reference Burns, Kurihara and Sano17
, Conjecture 7·3], and hence also the Rubin–Stark conjecture, is a consequence of
$K/k$
, the conjecture [
Reference Burns, Kurihara and Sano17
, Conjecture 7·3], and hence also the Rubin–Stark conjecture, is a consequence of
 $\mathrm{eTNC}(K/k)$
. Using functoriality properties of the eTNC, one thus obtains the validity of both the Burns–Kurihara–Sano and Rubin–Stark conjectures for any
$\mathrm{eTNC}(K/k)$
. Using functoriality properties of the eTNC, one thus obtains the validity of both the Burns–Kurihara–Sano and Rubin–Stark conjectures for any
 $K / k$
(and Rubin datum) such that
$K / k$
(and Rubin datum) such that
 $F \subseteq k \subseteq K \subseteq H$
, with
$F \subseteq k \subseteq K \subseteq H$
, with
 $H / F$
a finite Galois extension for which
$H / F$
a finite Galois extension for which
 $\mathrm{eTNC} (H / F)$
holds. The same conclusion is true if the ‘minus part’
$\mathrm{eTNC} (H / F)$
holds. The same conclusion is true if the ‘minus part’
 $\mathrm{eTNC}^- (H / F)$
of
$\mathrm{eTNC}^- (H / F)$
of
 $\mathrm{eTNC} (H / F)$
holds and k is totally real and K is totally imaginary.
$\mathrm{eTNC} (H / F)$
holds and k is totally real and K is totally imaginary.In this direction, the following is currently known:
-
(i)
 $\mathrm{eTNC} (H / F)$
holds if
$\mathrm{eTNC} (H / F)$
holds if
 $[H:F]=2$
; this case is proved by Kim [
Reference Kim36
, Section 2·4];
$[H:F]=2$
; this case is proved by Kim [
Reference Kim36
, Section 2·4]; -
(ii)
 $\mathrm{eTNC} (H / F)$
holds if
$\mathrm{eTNC} (H / F)$
holds if
 $F = {\mathbb{Q}}$
; this is work of Burns and Greither [
Reference Burns and Greither15
] with additional arguments for the 2-component by Flach [
Reference Flach28
];
$F = {\mathbb{Q}}$
; this is work of Burns and Greither [
Reference Burns and Greither15
] with additional arguments for the 2-component by Flach [
Reference Flach28
]; -
(iii)
 $\mathrm{eTNC} (H / F)$
holds if F an imaginary quadratic field such that all prime divisors of
$\mathrm{eTNC} (H / F)$
holds if F an imaginary quadratic field such that all prime divisors of
 $[H : F]$
split in k or validate Iwasawa’s
$[H : F]$
split in k or validate Iwasawa’s
 $\mu$
-vanishing conjecture; this case is proved by Hofer and the first author [
Reference Bullach and Hofer11
, Theorem B] and extends previous work of Bley [
Reference Bley2
,
Reference Bley3
,
Reference Bley4
].
$\mu$
-vanishing conjecture; this case is proved by Hofer and the first author [
Reference Bullach and Hofer11
, Theorem B] and extends previous work of Bley [
Reference Bley2
,
Reference Bley3
,
Reference Bley4
]. -
(iv)
 $\mathrm{eTNC} (H / F)^-$
holds if F is a totally real field and H is CM; this is work of the first author, Burns, Daoud and Seo [
Reference Bullach, Burns, Daoud and Seo10
] with additional arguments for the 2-component by Dasgupta, Kakde and Silliman [
Reference Dasgupta, Kakde and Silliman22
]. Earlier work in this direction includes [
Reference Atsuta and Kataoka1
,
Reference Nickel41
,
Reference Nickel42
,
Reference Nickel44
]. (The results in [
Reference Bullach, Burns, Daoud and Seo10
] crucially rely on work of Dasgupta and Kakde [
Reference Dasgupta and Kakde21
] on the Strong Brumer–Stark conjecture, and we remark that the Rubin–Stark conjecture can alternatively be directly deduced from the Strong Brumer–Stark conjecture, see [
Reference Dasgupta and Kakde21
, Theorem 1·6]).
$\mathrm{eTNC} (H / F)^-$
holds if F is a totally real field and H is CM; this is work of the first author, Burns, Daoud and Seo [
Reference Bullach, Burns, Daoud and Seo10
] with additional arguments for the 2-component by Dasgupta, Kakde and Silliman [
Reference Dasgupta, Kakde and Silliman22
]. Earlier work in this direction includes [
Reference Atsuta and Kataoka1
,
Reference Nickel41
,
Reference Nickel42
,
Reference Nickel44
]. (The results in [
Reference Bullach, Burns, Daoud and Seo10
] crucially rely on work of Dasgupta and Kakde [
Reference Dasgupta and Kakde21
] on the Strong Brumer–Stark conjecture, and we remark that the Rubin–Stark conjecture can alternatively be directly deduced from the Strong Brumer–Stark conjecture, see [
Reference Dasgupta and Kakde21
, Theorem 1·6]).
-
Further examples of, not necessarily abelian, extensions
 $H / F$
for which
$H / F$
for which
 $\mathrm{eTNC}(H/F)$
is known at present include the following:
$\mathrm{eTNC}(H/F)$
is known at present include the following:-
(i) H is a totally real Galois extension of
 $F = {\mathbb{Q}}$
such that either
$F = {\mathbb{Q}}$
such that either
 $\mathrm{Gal}({K}/{{\mathbb{Q}}}) \cong S_3$
and H has discriminant less than
$\mathrm{Gal}({K}/{{\mathbb{Q}}}) \cong S_3$
and H has discriminant less than
 $10^{20}$
or
$10^{20}$
or
 $\mathrm{Gal}({H}/{{\mathbb{Q}}}) \cong D_{12}$
and H has discriminant less than
$\mathrm{Gal}({H}/{{\mathbb{Q}}}) \cong D_{12}$
and H has discriminant less than
 $10^{30}$
; by Hofmann, Johnston, and Nickel [
Reference Johnston and Nickel34
, Corollary A·3].
$10^{30}$
; by Hofmann, Johnston, and Nickel [
Reference Johnston and Nickel34
, Corollary A·3]. -
(ii) a particular family of Quaternionic extensions H of
 $F=\mathbb{Q}$
; by Burns and Flach [
Reference Burns and Flach14
, Theorem 4·1].
$F=\mathbb{Q}$
; by Burns and Flach [
Reference Burns and Flach14
, Theorem 4·1]. -
(iii) one example of a Galois extension H of
 $F=\mathbb{Q}$
with
$F=\mathbb{Q}$
with
 $\mathrm{Gal}({H}/{{\mathbb{Q}}}) \cong A_4$
; numerical verification by Navilarekallu [
Reference Navilarekallu40
].
$\mathrm{Gal}({H}/{{\mathbb{Q}}}) \cong A_4$
; numerical verification by Navilarekallu [
Reference Navilarekallu40
]. -
(iv) when a number of standard conjectures are known to be valid, further results can be deduced from the examples above, see [ Reference Johnston and Nickel32 , Section 4] and [ Reference Johnston and Nickel34 , Section 10].
-
2. Preliminaries
In this preliminary section we review various constructions that will be useful in the sequel.
2·1. Rubin–Stark elements
Let
![]() $K/k$
be a finite abelian extension of number fields with Galois group
$K/k$
be a finite abelian extension of number fields with Galois group
![]() $G \,{:\!=}\, \mathrm{Gal}({K}/{k})$
and let (S, V, T) be a Rubin datum for
$G \,{:\!=}\, \mathrm{Gal}({K}/{k})$
and let (S, V, T) be a Rubin datum for
![]() $K / k$
. We fix a labelling
$K / k$
. We fix a labelling
![]() $S = \{ v_0, \dots, v_{|S| - 1} \}$
such that
$S = \{ v_0, \dots, v_{|S| - 1} \}$
such that
![]() $V = \{ v_1, \dots, v_{|V|} \}$
along with an extension
$V = \{ v_1, \dots, v_{|V|} \}$
along with an extension
![]() $w_i$
to K of each place
$w_i$
to K of each place
![]() $v_i$
in S. The ‘Rubin–Stark element’
$v_i$
in S. The ‘Rubin–Stark element’
![]() $\varepsilon^V_{K / k, S, T}$
for (S, V, T) is then the unique element of
$\varepsilon^V_{K / k, S, T}$
for (S, V, T) is then the unique element of
![]() ${\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}^\times_{K, S}$
with the property that
${\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}^\times_{K, S}$
with the property that
with
![]() $\bigwedge\nolimits^{|V|} \lambda_{K, S} {\colon} {\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}^\times_{K, S} \stackrel{\simeq}{\longrightarrow} {\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} X_{K, S}$
the isomorphism induced by (1·1).
$\bigwedge\nolimits^{|V|} \lambda_{K, S} {\colon} {\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}^\times_{K, S} \stackrel{\simeq}{\longrightarrow} {\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} X_{K, S}$
the isomorphism induced by (1·1).
Definition 2·1 . We define a
![]() ${\mathbb{Z}} [G]$
-submodule of
${\mathbb{Z}} [G]$
-submodule of
![]() ${\mathbb{R}} [G]$
by setting
${\mathbb{R}} [G]$
by setting
where
![]() $F (\varepsilon^V_{K / k, S, T})$
denotes the image of
$F (\varepsilon^V_{K / k, S, T})$
denotes the image of
![]() $(\varepsilon^V_{K / k, S, T}, F)$
under the determinant pairing
$(\varepsilon^V_{K / k, S, T}, F)$
under the determinant pairing
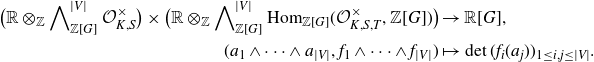 \begin{align*}\big( {\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}^\times_{K, S} \big)\times\big( {\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathrm{Hom}_{{\mathbb{Z}} [G]}( \mathcal{O}^\times_{K, S, T}, {\mathbb{Z}} [G]) \big)& \to {\mathbb{R}} [G], \\(a_1 \wedge \dots \wedge a_{|V|}, f_1 \wedge \dots \wedge f_{|V|} )& \mapsto \det ( f_i ( a_j))_{1 \leq i, j \leq |V|}.\end{align*}
\begin{align*}\big( {\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}^\times_{K, S} \big)\times\big( {\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathrm{Hom}_{{\mathbb{Z}} [G]}( \mathcal{O}^\times_{K, S, T}, {\mathbb{Z}} [G]) \big)& \to {\mathbb{R}} [G], \\(a_1 \wedge \dots \wedge a_{|V|}, f_1 \wedge \dots \wedge f_{|V|} )& \mapsto \det ( f_i ( a_j))_{1 \leq i, j \leq |V|}.\end{align*}
The following result was used in section 1·3 to reformulate both the Rubin–Stark conjecture and the Burns–Kurihara–Sano conjecture in terms of the more explicit products of the form (1·2).
Lemma 2·2. For any Rubin datum (S, V, T) for
![]() $K / k$
, one has an equality
$K / k$
, one has an equality
Proof. This is an immediate consequence of [ Reference Macías Castillo37 , Lemma 2·2].
2·2. Weil-étale cohomology complexes
We briefly recall key properties of a useful family of complexes constructed by Burns, Kurihara, and Sano in [
Reference Burns, Kurihara and Sano17
]. To do so, we let
![]() $K/F$
be an arbitrary finite Galois extension of number fields with Galois group
$K/F$
be an arbitrary finite Galois extension of number fields with Galois group
![]() $\Delta_F\,{:\!=}\,\mathrm{Gal}({K}/{F})$
.
$\Delta_F\,{:\!=}\,\mathrm{Gal}({K}/{F})$
.
We write
![]() $D(\mathbb{Z}[\Delta_F])$
for the derived category of
$D(\mathbb{Z}[\Delta_F])$
for the derived category of
![]() $\mathbb{Z}[\Delta_F]$
-modules and
$\mathbb{Z}[\Delta_F]$
-modules and
![]() $D^{\mathrm{p}}(\mathbb{Z}[\Delta_F])$
for its full triangulated subcategory comprising complexes that are ‘perfect’, that is, isomorphic (in
$D^{\mathrm{p}}(\mathbb{Z}[\Delta_F])$
for its full triangulated subcategory comprising complexes that are ‘perfect’, that is, isomorphic (in
![]() $D(\mathbb{Z}[\Delta_F])$
) to a bounded complex of finitely generated projective
$D(\mathbb{Z}[\Delta_F])$
) to a bounded complex of finitely generated projective
![]() $\mathbb{Z}[\Delta_F]$
-modules.
$\mathbb{Z}[\Delta_F]$
-modules.
Lemma 2·3. Fix sets S and T of places of F that satisfy the conditions (H1) and (H3) in section 1 with k replaced by F. Then the ‘Weil-ètale cohomology complex’
constructed in [
Reference Burns, Kurihara and Sano17
, Proposition 2·4] is an object of
![]() $D^{\mathrm{p}}(\mathbb{Z}[\Delta_F])$
that has the following properties:
$D^{\mathrm{p}}(\mathbb{Z}[\Delta_F])$
that has the following properties:
-
(i)
 $C^\bullet_{K,S,T}$
is acyclic outside degrees zero and one, with
$C^\bullet_{K,S,T}$
is acyclic outside degrees zero and one, with
 $H^0(C^\bullet_{K,S,T})=\mathcal{O}_{K,S,T}^\times$
, and the ‘transpose Selmer group’
$H^0(C^\bullet_{K,S,T})=\mathcal{O}_{K,S,T}^\times$
, and the ‘transpose Selmer group’
 $\mathrm{Sel}^{\mathrm{tr}}_{K,S,T} \,{:\!=}\, H^1(C^\bullet_{K,S,T})$
lies in a short exact sequence of
$\mathrm{Sel}^{\mathrm{tr}}_{K,S,T} \,{:\!=}\, H^1(C^\bullet_{K,S,T})$
lies in a short exact sequence of
 $\Delta_F$
-modules
$\Delta_F$
-modules  \begin{align*} 0\longrightarrow {\mathrm{Cl}}_{K,S,T}\longrightarrow \mathrm{Sel}^{\mathrm{tr}}_{K,S,T}\longrightarrow X_{K,S}\longrightarrow 0;\end{align*}
\begin{align*} 0\longrightarrow {\mathrm{Cl}}_{K,S,T}\longrightarrow \mathrm{Sel}^{\mathrm{tr}}_{K,S,T}\longrightarrow X_{K,S}\longrightarrow 0;\end{align*}
-
(ii)
 $C^\bullet_{K,S,T}$
is isomorphic in
$C^\bullet_{K,S,T}$
is isomorphic in
 $D(\mathbb{Z}[\Delta_F])$
to a complex
$D(\mathbb{Z}[\Delta_F])$
to a complex
 $[P_0 \stackrel{\phi}{\to} P_1]$
in which
$[P_0 \stackrel{\phi}{\to} P_1]$
in which
 $P_0$
is finitely generated projective (and placed in degree 0) while
$P_0$
is finitely generated projective (and placed in degree 0) while
 $P_1$
is free of finite rank;
$P_1$
is free of finite rank; -
(iii) for any normal subgroup
 $\Gamma$
of
$\Gamma$
of
 $\Delta_F$
there is, in
$\Delta_F$
there is, in
 $D^{\mathrm{p}}(\mathbb{Z}[\Delta_F/\Gamma])$
, a canonical isomorphism
$D^{\mathrm{p}}(\mathbb{Z}[\Delta_F/\Gamma])$
, a canonical isomorphism  \[\mathbb{Z}[\Delta_F/\Gamma]\otimes^{\mathbb{L}}_{\mathbb{Z}[\Delta_F]}C^\bullet_{K,S,T}\cong C^\bullet_{K^\Gamma,S,T}.\]
\[\mathbb{Z}[\Delta_F/\Gamma]\otimes^{\mathbb{L}}_{\mathbb{Z}[\Delta_F]}C^\bullet_{K,S,T}\cong C^\bullet_{K^\Gamma,S,T}.\]
Proof.
![]() $C^\bullet_{K,S,T}$
is an object of
$C^\bullet_{K,S,T}$
is an object of
![]() $D^{\mathrm{p}}(\mathbb{Z}[\Delta_F])$
by choice of S and by [
Reference Burns, Kurihara and Sano17
, Proposition 2·4 (iv)]. Claim (i) is [
Reference Burns, Kurihara and Sano17
Remark 2·7], Claim (ii) is proved in [
Reference Burns, Kurihara and Sano17
, Section 5·4]. Claim (iii) follows from the diagram in [
Reference Burns, Kurihara and Sano17
, Proposition 2·4 (i)], and the functoriality properties of étale cohomology.
$D^{\mathrm{p}}(\mathbb{Z}[\Delta_F])$
by choice of S and by [
Reference Burns, Kurihara and Sano17
, Proposition 2·4 (iv)]. Claim (i) is [
Reference Burns, Kurihara and Sano17
Remark 2·7], Claim (ii) is proved in [
Reference Burns, Kurihara and Sano17
, Section 5·4]. Claim (iii) follows from the diagram in [
Reference Burns, Kurihara and Sano17
, Proposition 2·4 (i)], and the functoriality properties of étale cohomology.
3. The proof of Theorem 1·3
3·1. The proof in case (i)
In this subsection we assume the hypotheses of Theorem 1·3 (i). In particular,
![]() $\Delta \,{:\!=}\, \mathrm{Gal}({K}/{\kappa})$
is isomorphic to
$\Delta \,{:\!=}\, \mathrm{Gal}({K}/{\kappa})$
is isomorphic to
![]() ${\mathrm{Aff}} (q)$
, and (S, V, T) is a Rubin datum for
${\mathrm{Aff}} (q)$
, and (S, V, T) is a Rubin datum for
![]() $K / k$
with
$K / k$
with
![]() $|S| \gt |V| + 1$
. We recall that
$|S| \gt |V| + 1$
. We recall that
![]() ${\mathrm{Aff}} (q)$
is isomorphic to the semidirect product
${\mathrm{Aff}} (q)$
is isomorphic to the semidirect product
![]() $\mathbb{F}_q\rtimes\mathbb{F}_q^\times$
with the natural action (see for instance [
Reference Johnston and Nickel32
, Example 2·16]).
$\mathbb{F}_q\rtimes\mathbb{F}_q^\times$
with the natural action (see for instance [
Reference Johnston and Nickel32
, Example 2·16]).
Since
![]() $G = \mathrm{Gal}({K}/{k})$
is abelian, the complex
$G = \mathrm{Gal}({K}/{k})$
is abelian, the complex
![]() $C^\bullet_{K,S,T}$
in
$C^\bullet_{K,S,T}$
in
![]() $D^{\mathrm{p}}(\mathbb{Z}[G])$
admits a well-defined determinant
$D^{\mathrm{p}}(\mathbb{Z}[G])$
admits a well-defined determinant
![]() ${\mathrm{Det}}_{{\mathbb{Z}} [G]} (C^\bullet_{K, S, T})$
(in the sense of Knudsen–Mumford). We then also use the ‘zeta element’
${\mathrm{Det}}_{{\mathbb{Z}} [G]} (C^\bullet_{K, S, T})$
(in the sense of Knudsen–Mumford). We then also use the ‘zeta element’
![]() $z_{K / k, S, T} \in {\mathbb{R}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
, the definition of which can be found in [
Reference Burns, Kurihara and Sano17
, Definition 3·5] and will be recalled in the course of the proof of Lemma 3·1 below. For the moment we only note that
$z_{K / k, S, T} \in {\mathbb{R}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
, the definition of which can be found in [
Reference Burns, Kurihara and Sano17
, Definition 3·5] and will be recalled in the course of the proof of Lemma 3·1 below. For the moment we only note that
![]() $z_{K / k, S, T}$
is by construction an
$z_{K / k, S, T}$
is by construction an
![]() ${\mathbb{R}} [G]$
-basis of the free rank-one
${\mathbb{R}} [G]$
-basis of the free rank-one
![]() ${\mathbb{R}} [G]$
-module
${\mathbb{R}} [G]$
-module
![]() ${\mathbb{R}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
.
${\mathbb{R}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
.
Lemma 3·1. The following claims are valid.
-
(a) The zeta element
 $z_{K / k, S, T}$
belongs to
$z_{K / k, S, T}$
belongs to
 ${\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
. In particular,
${\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
. In particular,
 $z_{K / k, S, T}$
is a
$z_{K / k, S, T}$
is a
 ${\mathbb{Q}} [G]$
-basis of the free rank-one
${\mathbb{Q}} [G]$
-basis of the free rank-one
 ${\mathbb{Q}} [G]$
-module
${\mathbb{Q}} [G]$
-module
 ${\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
.
${\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
. -
(b) For every prime number
 $\ell$
, there exists an element
$\ell$
, there exists an element
 $\mathfrak{z}^{(\ell)}_{K / k, S, T}$
of
$\mathfrak{z}^{(\ell)}_{K / k, S, T}$
of
 ${\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
with the following properties:
${\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
with the following properties:-
(i) the
 ${\mathbb{Z}} [G]$
-submodule of
${\mathbb{Z}} [G]$
-submodule of
 ${\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
generated by
${\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
generated by
 $\mathfrak{z}^{(\ell)}_{K / k, S, T}$
has prime-to-
$\mathfrak{z}^{(\ell)}_{K / k, S, T}$
has prime-to-
 $\ell$
index;
$\ell$
index; -
(ii) the unique element
 $\lambda^{(\ell)} \in {\mathbb{Q}} [G]$
defined by
$\lambda^{(\ell)} \in {\mathbb{Q}} [G]$
defined by
 $z_{K / k, S, T} = \lambda^{(\ell)} \cdot \mathfrak{z}^{(\ell)}_{K / k, S, T}$
belongs to the image of the map where
$z_{K / k, S, T} = \lambda^{(\ell)} \cdot \mathfrak{z}^{(\ell)}_{K / k, S, T}$
belongs to the image of the map where \[\rho_{\Delta / G} {\colon} \zeta({\mathbb{C}} [\Delta]) \to {\mathbb{C}} [G], \quad x \mapsto \sum_{\chi \in \widehat{G}} \big( \prod_{\psi \in \widehat{\Delta}} \psi (x)^{\langle \psi, \mathrm{Ind}_G^\Delta( \chi) \rangle} \big) \cdot e_\chi,\]
\[\rho_{\Delta / G} {\colon} \zeta({\mathbb{C}} [\Delta]) \to {\mathbb{C}} [G], \quad x \mapsto \sum_{\chi \in \widehat{G}} \big( \prod_{\psi \in \widehat{\Delta}} \psi (x)^{\langle \psi, \mathrm{Ind}_G^\Delta( \chi) \rangle} \big) \cdot e_\chi,\]
 $\widehat{\Delta}$
is the set of irreducible characters of
$\widehat{\Delta}$
is the set of irreducible characters of
 $\Delta$
,
$\Delta$
,
 $\langle \cdot, \cdot \rangle$
denotes the inner product of characters,
$\langle \cdot, \cdot \rangle$
denotes the inner product of characters,
 $\zeta({\mathbb{C}} [\Delta]) \cong \prod_{\psi \in \widehat{\Delta}} {\mathbb{C}}$
denotes the centre of
$\zeta({\mathbb{C}} [\Delta]) \cong \prod_{\psi \in \widehat{\Delta}} {\mathbb{C}}$
denotes the centre of
 ${\mathbb{C}} [\Delta]$
, and we have written
${\mathbb{C}} [\Delta]$
, and we have written
 $\psi$
for the map
$\psi$
for the map
 $\zeta({\mathbb{C}} [\Delta]) \to {\mathbb{C}}$
induced by
$\zeta({\mathbb{C}} [\Delta]) \to {\mathbb{C}}$
induced by
 $\psi$
.
$\psi$
.
-
Proof. Claim (a) is equivalent to Stark’s conjecture for
![]() $K / k$
(cf. [
Reference Flach27
, Theorem 7·1 b)]). Since any non-trivial (irreducible) character of G induces a rational-valued character of
$K / k$
(cf. [
Reference Flach27
, Theorem 7·1 b)]). Since any non-trivial (irreducible) character of G induces a rational-valued character of
![]() $\Delta$
(see, for example, [
Reference Motose39
, Theorem 5]), the validity of Stark’s conjecture follows from Tate’s proof of Stark’s conjecture for rational-valued characters in [
Reference Tate56
, Chapter II, Theorem 6·8].
$\Delta$
(see, for example, [
Reference Motose39
, Theorem 5]), the validity of Stark’s conjecture follows from Tate’s proof of Stark’s conjecture for rational-valued characters in [
Reference Tate56
, Chapter II, Theorem 6·8].
To prove claim (b), we may enlarge S and T since, if S’ and T’ are respective disjoint finite oversets of S and T, then the exact triangles in [ Reference Burns, Kurihara and Sano17 , Proposition 2·4, (ii) and right-hand column of (6) in (i)] induce an isomorphism
that maps
![]() $z_{K / k, S', T'}$
to
$z_{K / k, S', T'}$
to
![]() $z_{K / k, S, T}$
. We therefore may and will assume that S contains all places that are ramified in
$z_{K / k, S, T}$
. We therefore may and will assume that S contains all places that are ramified in
![]() $K / \kappa$
and that both S and T are stable under the action of
$K / \kappa$
and that both S and T are stable under the action of
![]() $\Delta$
.
$\Delta$
.
Since the complex
![]() $C^\bullet_{K,S,T}$
depends only on K,
$C^\bullet_{K,S,T}$
depends only on K,
![]() $S_K$
and
$S_K$
and
![]() $T_K$
, we may then regard it also as an object of
$T_K$
, we may then regard it also as an object of
![]() $D^{\mathrm{p}}(\mathbb{Z}[\Delta])$
. We fix a representative of
$D^{\mathrm{p}}(\mathbb{Z}[\Delta])$
. We fix a representative of
![]() $C^\bullet_{K,S,T}$
in
$C^\bullet_{K,S,T}$
in
![]() $D(\mathbb{Z}[\Delta])$
as in Lemma 2·3 (ii) (applied to
$D(\mathbb{Z}[\Delta])$
as in Lemma 2·3 (ii) (applied to
![]() $F = \kappa$
). We note that (1·1) combines with the Noether–Deuring Theorem to imply that
$F = \kappa$
). We note that (1·1) combines with the Noether–Deuring Theorem to imply that
![]() ${\mathbb{Q}} \otimes_{\mathbb{Z}} P_0 \cong {\mathbb{Q}} \otimes_{\mathbb{Z}} P_1$
. For every prime number
${\mathbb{Q}} \otimes_{\mathbb{Z}} P_0 \cong {\mathbb{Q}} \otimes_{\mathbb{Z}} P_1$
. For every prime number
![]() $\ell$
, Roiter’s Lemma [
Reference Curtis and Reiner20
, (31·6)] then gives the existence of an injection
$\ell$
, Roiter’s Lemma [
Reference Curtis and Reiner20
, (31·6)] then gives the existence of an injection
![]() $i^{(\ell)} {\colon} P_1 \hookrightarrow P_0$
with finite cokernel of order prime to
$i^{(\ell)} {\colon} P_1 \hookrightarrow P_0$
with finite cokernel of order prime to
![]() $\ell$
.
$\ell$
.
We fix a set
![]() $\{ \sigma_1, \dots, \sigma_{(\Delta : G)}\}$
of representatives for
$\{ \sigma_1, \dots, \sigma_{(\Delta : G)}\}$
of representatives for
![]() $\Delta / G$
and choose an ordered
$\Delta / G$
and choose an ordered
![]() ${\mathbb{Z}} [\Delta]$
-basis
${\mathbb{Z}} [\Delta]$
-basis
![]() $\mathfrak{B} = \{ b_1, \dots, b_d \}$
of
$\mathfrak{B} = \{ b_1, \dots, b_d \}$
of
![]() $P_1$
. Then
$P_1$
. Then
![]() $P_1$
is also a free
$P_1$
is also a free
![]() ${\mathbb{Z}} [G]$
-module, with (ordered)
${\mathbb{Z}} [G]$
-module, with (ordered)
![]() ${\mathbb{Z}} [G]$
-basis
${\mathbb{Z}} [G]$
-basis
We also define ordered sets
![]() $\mathfrak{C}^{(\ell)} \,{:\!=}\, \{ i^{(\ell)} (b) \mid b \in \mathfrak{B} \}$
and
$\mathfrak{C}^{(\ell)} \,{:\!=}\, \{ i^{(\ell)} (b) \mid b \in \mathfrak{B} \}$
and
![]() ${\mathfrak{C}'}^{(\ell)} = \{ i^{(\ell)} (b) \mid b \in \mathfrak{B}'\}$
. Setting
${\mathfrak{C}'}^{(\ell)} = \{ i^{(\ell)} (b) \mid b \in \mathfrak{B}'\}$
. Setting
![]() $P_1^\ast \,{:\!=}\, \mathrm{Hom}_{{\mathbb{Z}} [G]} (P_1, {\mathbb{Z}} [G])$
, we now define
$P_1^\ast \,{:\!=}\, \mathrm{Hom}_{{\mathbb{Z}} [G]} (P_1, {\mathbb{Z}} [G])$
, we now define
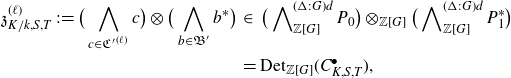 \begin{align*}\mathfrak{z}^{(\ell)}_{K / k, S, T} \,{:\!=}\, \big( \bigwedge_{c \in {\mathfrak{C}'}^{(\ell)}} c \big)\otimes \big( \bigwedge_{b \in \mathfrak{B}'} b^\ast \big)\; &\in \; \big( \bigwedge\nolimits_{{\mathbb{Z}} [G]}^{(\Delta : G)d} P_0 \big) \otimes_{{\mathbb{Z}} [G]} \big( \bigwedge\nolimits_{{\mathbb{Z}} [G]}^{(\Delta : G)d} P_1^\ast \big) \\&= {\mathrm{Det}}_{{\mathbb{Z}} [G]} (C^\bullet_{K, S, T}),\end{align*}
\begin{align*}\mathfrak{z}^{(\ell)}_{K / k, S, T} \,{:\!=}\, \big( \bigwedge_{c \in {\mathfrak{C}'}^{(\ell)}} c \big)\otimes \big( \bigwedge_{b \in \mathfrak{B}'} b^\ast \big)\; &\in \; \big( \bigwedge\nolimits_{{\mathbb{Z}} [G]}^{(\Delta : G)d} P_0 \big) \otimes_{{\mathbb{Z}} [G]} \big( \bigwedge\nolimits_{{\mathbb{Z}} [G]}^{(\Delta : G)d} P_1^\ast \big) \\&= {\mathrm{Det}}_{{\mathbb{Z}} [G]} (C^\bullet_{K, S, T}),\end{align*}
where
![]() $b^\ast {\colon} P_1 \to {\mathbb{Z}} [G]$
denotes the
$b^\ast {\colon} P_1 \to {\mathbb{Z}} [G]$
denotes the
![]() ${\mathbb{Z}} [G]$
-linear dual of
${\mathbb{Z}} [G]$
-linear dual of
![]() $b \in P_1$
. By construction, the element
$b \in P_1$
. By construction, the element
![]() $\mathfrak{z}^{(\ell)}_{K / k, S, T}$
then has property (i).
$\mathfrak{z}^{(\ell)}_{K / k, S, T}$
then has property (i).
To justify claim (ii), we first recall the definition of the zeta element
![]() $z_{K / k, S, T}$
. Our fixed choice of representative for
$z_{K / k, S, T}$
. Our fixed choice of representative for
![]() $C^\bullet_{K, S, T}$
gives rise to exact sequences
$C^\bullet_{K, S, T}$
gives rise to exact sequences
![]() $0 \to \mathcal{O}_{K,S, T}^\times \to P_0 \to \phi (P_0) \to 0$
and
$0 \to \mathcal{O}_{K,S, T}^\times \to P_0 \to \phi (P_0) \to 0$
and
![]() $\phi (P_0) \to P_1 \to \mathrm{Sel}^{\mathrm{tr}}_{K,S,T} \to 0$
of
$\phi (P_0) \to P_1 \to \mathrm{Sel}^{\mathrm{tr}}_{K,S,T} \to 0$
of
![]() ${\mathbb{Z}} [\Delta]$
-modules for which we may choose
${\mathbb{Z}} [\Delta]$
-modules for which we may choose
![]() ${\mathbb{R}} [\Delta]$
-splittings
${\mathbb{R}} [\Delta]$
-splittings
Given this, we define the composite isomorphism of
![]() ${\mathbb{R}} [\Delta]$
-modules
${\mathbb{R}} [\Delta]$
-modules
where
![]() $\lambda_{K, S}$
denotes the Dirichlet regulator map defined in (1·1). We write
$\lambda_{K, S}$
denotes the Dirichlet regulator map defined in (1·1). We write
![]() $A^{(\ell)}$
for the matrix in
$A^{(\ell)}$
for the matrix in
![]() $\mathrm{GL}_{(\Delta : G) d} ( {\mathbb{R}} [G])$
that represents
$\mathrm{GL}_{(\Delta : G) d} ( {\mathbb{R}} [G])$
that represents
![]() $\alpha$
with respect to the bases
$\alpha$
with respect to the bases
![]() ${\mathfrak{C}'}^{(\ell)}$
and
${\mathfrak{C}'}^{(\ell)}$
and
![]() $\mathfrak{B}'$
.
$\mathfrak{B}'$
.
We consider the ‘leading term’
where
![]() $\check\psi$
denotes the contragredient of
$\check\psi$
denotes the contragredient of
![]() $\psi$
and
$\psi$
and
![]() $L^\ast_{\kappa, S, T} (\check\psi, 0)$
is the leading term of
$L^\ast_{\kappa, S, T} (\check\psi, 0)$
is the leading term of
![]() $L_{\kappa, S, T} (\check\psi, s)$
at
$L_{\kappa, S, T} (\check\psi, s)$
at
![]() $s = 0$
. Similarly, we set
$s = 0$
. Similarly, we set
![]() $\theta^\ast_{K / k, S, T} (0) \,{:\!=}\,\sum_{\chi \in \widehat{G}} L^\ast_{k, S, T} (\check\chi, 0) e_{\chi}\in\mathbb{R}[G]^\times$
. One then has that
$\theta^\ast_{K / k, S, T} (0) \,{:\!=}\,\sum_{\chi \in \widehat{G}} L^\ast_{k, S, T} (\check\chi, 0) e_{\chi}\in\mathbb{R}[G]^\times$
. One then has that
![]() $z_{K / k, S, T} = \lambda^{(\ell)} \cdot \mathfrak{z}^{(\ell)}_{K / k, S, T}$
with
$z_{K / k, S, T} = \lambda^{(\ell)} \cdot \mathfrak{z}^{(\ell)}_{K / k, S, T}$
with
![]() $\lambda^{(\ell)} \in {\mathbb{R}} [G]^\times$
the unique element such that
$\lambda^{(\ell)} \in {\mathbb{R}} [G]^\times$
the unique element such that
![]() $\lambda^{(\ell)} \cdot {\det}_{{\mathbb{R}} [G]} ( A^{(\ell)}) = \theta^\ast_{K / k, S, T} (0) $
. The reduced norm of the matrix
$\lambda^{(\ell)} \cdot {\det}_{{\mathbb{R}} [G]} ( A^{(\ell)}) = \theta^\ast_{K / k, S, T} (0) $
. The reduced norm of the matrix
![]() $B^{(\ell)} \in \mathrm{GL}_d ({\mathbb{R}} [\Delta])$
that represents
$B^{(\ell)} \in \mathrm{GL}_d ({\mathbb{R}} [\Delta])$
that represents
![]() $\alpha$
with respect to the bases
$\alpha$
with respect to the bases
![]() $\mathfrak{C}^{(\ell)}$
and
$\mathfrak{C}^{(\ell)}$
and
![]() $\mathfrak{B}$
belongs to
$\mathfrak{B}$
belongs to
![]() $\zeta(\mathbb{R}[\Delta])^\times$
, and we define a scalar
$\zeta(\mathbb{R}[\Delta])^\times$
, and we define a scalar
![]() $\mu^{(\ell)} \in \zeta({\mathbb{R}} [\Delta])^\times$
by
$\mu^{(\ell)} \in \zeta({\mathbb{R}} [\Delta])^\times$
by
By the functoriality of reduced norms under restriction to subgroups (see, for example, [
Reference Breuning5
, bottom of p. 291]) one has
![]() $\rho_{\Delta/G}(\mathrm{Nrd}_{{\mathbb{R}} [\Delta]} ( B^{(\ell)}))={\det}_{{\mathbb{R}} [G]} ( A^{(\ell)})$
and thus also
$\rho_{\Delta/G}(\mathrm{Nrd}_{{\mathbb{R}} [\Delta]} ( B^{(\ell)}))={\det}_{{\mathbb{R}} [G]} ( A^{(\ell)})$
and thus also
from which we deduce that
![]() $\rho_{\Delta / G} ( \mu^{(\ell)}) = \lambda^{(\ell)}$
. This concludes the proof of claim (b).
$\rho_{\Delta / G} ( \mu^{(\ell)}) = \lambda^{(\ell)}$
. This concludes the proof of claim (b).
We now give the proof of Theorem 1·3 in case (i). Since
![]() $\Delta \cong {\mathrm{Aff}} (q)$
, one has that
$\Delta \cong {\mathrm{Aff}} (q)$
, one has that
![]() $\widehat{\Delta}$
consists of the linear characters of
$\widehat{\Delta}$
consists of the linear characters of
![]() $\Delta / G$
and the unique irreducible character of degree
$\Delta / G$
and the unique irreducible character of degree
![]() $q - 1$
that is obtained as
$q - 1$
that is obtained as
![]() $\psi_{\mathrm{nl}} \,{:\!=}\, \mathrm{Ind}_G^\Delta (\chi)$
for any non-trivial (irreducible) character
$\psi_{\mathrm{nl}} \,{:\!=}\, \mathrm{Ind}_G^\Delta (\chi)$
for any non-trivial (irreducible) character
![]() $\chi$
of G (see, for example, [
Reference Motose39
, Theorem 5]). As a consequence, one has
$\chi$
of G (see, for example, [
Reference Motose39
, Theorem 5]). As a consequence, one has
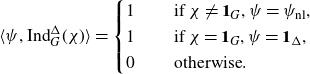 \[\langle \psi, \mathrm{Ind}_G^\Delta( \chi) \rangle =\begin{cases}1 \quad & \text{ if } \chi \neq \mathbf{1}_G, \psi = \psi_{\mathrm{nl}}, \\1 & \text{ if } \chi = \mathbf{1}_G, \psi = \mathbf{1}_\Delta, \\0 & \text{ otherwise}.\end{cases}\]
\[\langle \psi, \mathrm{Ind}_G^\Delta( \chi) \rangle =\begin{cases}1 \quad & \text{ if } \chi \neq \mathbf{1}_G, \psi = \psi_{\mathrm{nl}}, \\1 & \text{ if } \chi = \mathbf{1}_G, \psi = \mathbf{1}_\Delta, \\0 & \text{ otherwise}.\end{cases}\]
For every prime number
![]() $\ell$
, the element
$\ell$
, the element
![]() $\lambda^{(\ell)}$
provided by Lemma 3·1 (b) (ii) is hence of the form
$\lambda^{(\ell)}$
provided by Lemma 3·1 (b) (ii) is hence of the form
![]() $\lambda^{(\ell)} = a e_{\mathbf{1}} + b (1 - e_{\mathbf{1}})$
for suitable
$\lambda^{(\ell)} = a e_{\mathbf{1}} + b (1 - e_{\mathbf{1}})$
for suitable
![]() $a, b \in {\mathbb{Q}}$
.
$a, b \in {\mathbb{Q}}$
.
Now, the isomorphism
![]() $\mathbb{Z}\otimes^\mathbb{L}_{{\mathbb{Z}} [G]}C^\bullet_{K, S, T} \cong C^\bullet_{k, S, T}$
in Lemma 2·3 (iii) induces an isomorphism
$\mathbb{Z}\otimes^\mathbb{L}_{{\mathbb{Z}} [G]}C^\bullet_{K, S, T} \cong C^\bullet_{k, S, T}$
in Lemma 2·3 (iii) induces an isomorphism
![]() $\mathbb{Z}\otimes_{\mathbb{Z}[G]}( {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})) \cong {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{k, S, T})$
that sends
$\mathbb{Z}\otimes_{\mathbb{Z}[G]}( {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})) \cong {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{k, S, T})$
that sends
![]() $1 \otimes z_{K / k, S, T}$
to
$1 \otimes z_{K / k, S, T}$
to
![]() $z_{k/k, S, T}$
. In addition, the analytic class number formula for k asserts that
$z_{k/k, S, T}$
. In addition, the analytic class number formula for k asserts that
![]() $z_{k/k, S, T}$
is a
$z_{k/k, S, T}$
is a
![]() ${\mathbb{Z}}$
-basis of the free rank-one
${\mathbb{Z}}$
-basis of the free rank-one
![]() ${\mathbb{Z}}$
-module
${\mathbb{Z}}$
-module
![]() ${\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{k, S, T})$
(cf. [
Reference Kato35
, Section 2·2·2] or [
Reference Burns12
, Exercise 2·6]).
${\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{k, S, T})$
(cf. [
Reference Kato35
, Section 2·2·2] or [
Reference Burns12
, Exercise 2·6]).
For each prime number
![]() $\ell$
, we write
$\ell$
, we write
![]() $\mathbb{Z}_{(\ell)}$
for the localisation of
$\mathbb{Z}_{(\ell)}$
for the localisation of
![]() $\mathbb{Z}$
at the prime ideal
$\mathbb{Z}$
at the prime ideal
![]() $\ell{\mathbb{Z}}$
. The definition of
$\ell{\mathbb{Z}}$
. The definition of
![]() $\mathfrak{z}_{K / k, S, T}^{(\ell)}$
then implies that both
$\mathfrak{z}_{K / k, S, T}^{(\ell)}$
then implies that both
![]() $1 \otimes \mathfrak{z}_{K / k, S, T}^{(\ell)}$
and
$1 \otimes \mathfrak{z}_{K / k, S, T}^{(\ell)}$
and
![]() $a \cdot (1 \otimes \mathfrak{z}_{K / k, S, T}^{(\ell)}) = 1 \otimes ( \lambda^{(\ell)} \mathfrak{z}_{K / k, S, T}^{(\ell)}) = 1 \otimes z_{K / k, S, T}$
are
$a \cdot (1 \otimes \mathfrak{z}_{K / k, S, T}^{(\ell)}) = 1 \otimes ( \lambda^{(\ell)} \mathfrak{z}_{K / k, S, T}^{(\ell)}) = 1 \otimes z_{K / k, S, T}$
are
![]() $\mathbb{Z}_{(\ell)}$
-bases of
$\mathbb{Z}_{(\ell)}$
-bases of
![]() $\mathbb{Z}\otimes_{\mathbb{Z}[G]}( \mathbb{Z}_{(\ell)} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})) $
. We conclude that a belongs to
$\mathbb{Z}\otimes_{\mathbb{Z}[G]}( \mathbb{Z}_{(\ell)} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})) $
. We conclude that a belongs to
![]() $\mathbb{Z}_{(\ell)}^\times$
.
$\mathbb{Z}_{(\ell)}^\times$
.
We next write
![]() $\mathrm{N} = \mathrm{N}_{{\mathbb{Q}} [G] / {\mathbb{Q}}} {\colon} {\mathbb{Q}} [G] \to {\mathbb{Q}}$
for the ring-theoretic norm map and note that the construction of [
Reference Bullach, Burns, Daoud and Seo10
, Lemma 3·7 (c)] gives the existence of an N-semilinear map
$\mathrm{N} = \mathrm{N}_{{\mathbb{Q}} [G] / {\mathbb{Q}}} {\colon} {\mathbb{Q}} [G] \to {\mathbb{Q}}$
for the ring-theoretic norm map and note that the construction of [
Reference Bullach, Burns, Daoud and Seo10
, Lemma 3·7 (c)] gives the existence of an N-semilinear map
![]() $\mathcal{F} {\colon} {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T}) \to {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{K, S, T})$
that sends
$\mathcal{F} {\colon} {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T}) \to {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{K, S, T})$
that sends
![]() $z_{K / k, S, T}$
to
$z_{K / k, S, T}$
to
![]() $z_{K / K, S, T}$
. Since
$z_{K / K, S, T}$
. Since
![]() $z_{K / K, S, T}$
is a
$z_{K / K, S, T}$
is a
![]() ${\mathbb{Z}}$
-basis of
${\mathbb{Z}}$
-basis of
![]() ${\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{K, S, T})$
by the analytic class number formula for K, we see that for each prime
${\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{K, S, T})$
by the analytic class number formula for K, we see that for each prime
![]() $\ell$
, both
$\ell$
, both
![]() $\mathcal{F} ( \mathfrak{z}_{K / k, S, T}^{(\ell)})$
and
$\mathcal{F} ( \mathfrak{z}_{K / k, S, T}^{(\ell)})$
and
![]() $z_{K / k, S, T} = \mathcal{F} ( z_{K / k, S, T}) = \mathcal{F} ( \lambda^{(\ell)} \mathfrak{z}_{K / k, S, T}^{(\ell)}) = \mathrm{N} ( \lambda^{(\ell)}) \cdot \mathcal{F} ( \mathfrak{z}_{K / k, S, T}^{(\ell)})$
are
$z_{K / k, S, T} = \mathcal{F} ( z_{K / k, S, T}) = \mathcal{F} ( \lambda^{(\ell)} \mathfrak{z}_{K / k, S, T}^{(\ell)}) = \mathrm{N} ( \lambda^{(\ell)}) \cdot \mathcal{F} ( \mathfrak{z}_{K / k, S, T}^{(\ell)})$
are
![]() ${\mathbb{Z}}_{(\ell)}$
-bases of
${\mathbb{Z}}_{(\ell)}$
-bases of
![]() ${\mathbb{Z}}_{(\ell)} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{K, S, T})$
. It follows that
${\mathbb{Z}}_{(\ell)} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{\mathbb{Z}} (C^\bullet_{K, S, T})$
. It follows that
![]() $\mathrm{N} (\lambda^{(\ell)}) = a b^{q - 1}$
must also belong to
$\mathrm{N} (\lambda^{(\ell)}) = a b^{q - 1}$
must also belong to
![]() ${\mathbb{Z}}_{(\ell)}^\times$
. Upon recalling that
${\mathbb{Z}}_{(\ell)}^\times$
. Upon recalling that
![]() $a \in {\mathbb{Z}}_{(\ell)}^\times$
by the above discussion, we conclude that
$a \in {\mathbb{Z}}_{(\ell)}^\times$
by the above discussion, we conclude that
![]() $b^{q - 1} \in {\mathbb{Z}}_{(\ell)}^\times$
. Since b is rational, we deduce that b belongs to
$b^{q - 1} \in {\mathbb{Z}}_{(\ell)}^\times$
. Since b is rational, we deduce that b belongs to
![]() ${\mathbb{Z}}_{(\ell)}^\times$
.
${\mathbb{Z}}_{(\ell)}^\times$
.
Define an idempotent
![]() $e_{K, S, V}$
of
$e_{K, S, V}$
of
![]() ${\mathbb{Q}} [G]$
as the sum
${\mathbb{Q}} [G]$
as the sum
![]() $\sum_\chi e_\chi$
of all primitive orthogonal idempotents
$\sum_\chi e_\chi$
of all primitive orthogonal idempotents
![]() $e_\chi$
associated with characters
$e_\chi$
associated with characters
![]() $\chi$
of G such that
$\chi$
of G such that
![]() $e_\chi$
annihilates
$e_\chi$
annihilates
![]() $\mathbb{C}\otimes_\mathbb{Z} X_{K, S \setminus V}$
.
$\mathbb{C}\otimes_\mathbb{Z} X_{K, S \setminus V}$
.
We then define a ‘projection map’
![]() $\Theta_{K / k, S}^V$
as the composite map
$\Theta_{K / k, S}^V$
as the composite map
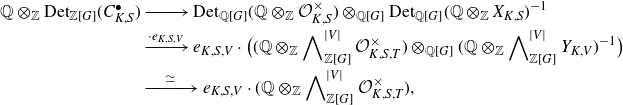 \begin{align} \nonumber {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S})& \xrightarrow{\phantom{\cdot e_{K, S, V}}} {\mathrm{Det}}_{{\mathbb{Q}} [G]} ( {\mathbb{Q}} \otimes_{\mathbb{Z}} \mathcal{O}_{K, S}^\times)\otimes_{{\mathbb{Q}} [G]} {\mathrm{Det}}_{{\mathbb{Q}} [G]} ( {\mathbb{Q}} \otimes_{\mathbb{Z}} X_{K, S})^{-1} \\ \nonumber& \xrightarrow{\cdot e_{K, S, V}}e_{K, S, V} \cdot \big ( ( {\mathbb{Q}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times)\otimes_{{\mathbb{Q}} [G]} ( {\mathbb{Q}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} Y_{K, V} )^{-1} \big) \\& \xrightarrow{\quad \simeq \quad} e_{K, S, V} \cdot ( {\mathbb{Q}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times),\end{align}
\begin{align} \nonumber {\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S})& \xrightarrow{\phantom{\cdot e_{K, S, V}}} {\mathrm{Det}}_{{\mathbb{Q}} [G]} ( {\mathbb{Q}} \otimes_{\mathbb{Z}} \mathcal{O}_{K, S}^\times)\otimes_{{\mathbb{Q}} [G]} {\mathrm{Det}}_{{\mathbb{Q}} [G]} ( {\mathbb{Q}} \otimes_{\mathbb{Z}} X_{K, S})^{-1} \\ \nonumber& \xrightarrow{\cdot e_{K, S, V}}e_{K, S, V} \cdot \big ( ( {\mathbb{Q}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times)\otimes_{{\mathbb{Q}} [G]} ( {\mathbb{Q}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} Y_{K, V} )^{-1} \big) \\& \xrightarrow{\quad \simeq \quad} e_{K, S, V} \cdot ( {\mathbb{Q}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times),\end{align}
where the first arrow is the natural ‘passage-to-cohomology’ map, the second map is induced by multiplication by
![]() $e_{K, S, V}$
, and the last arrow by the trivialisation
$e_{K, S, V}$
, and the last arrow by the trivialisation
![]() $\bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} Y_{K, V} \cong {\mathbb{Z}} [G]$
that is afforded by sending
$\bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} Y_{K, V} \cong {\mathbb{Z}} [G]$
that is afforded by sending
![]() $\bigwedge\nolimits_{1 \leq i \leq |V|} w_i$
to 1.
$\bigwedge\nolimits_{1 \leq i \leq |V|} w_i$
to 1.
Note that our hypothesis
![]() $|S| \gt |V| + 1$
combines with the short exact sequence
$|S| \gt |V| + 1$
combines with the short exact sequence
![]() $0\to X_{K,S\setminus V}\to X_{K,S}\to Y_{K,V}\to 0$
to imply that
$0\to X_{K,S\setminus V}\to X_{K,S}\to Y_{K,V}\to 0$
to imply that
![]() $e_{\mathbf{1}}\cdot e_{K, S, V}=0$
. In particular, we have
$e_{\mathbf{1}}\cdot e_{K, S, V}=0$
. In particular, we have
![]() $\lambda^{(\ell)} \cdot e_{K, S, V} = (a e_{\mathbf{1}} + b ( 1 - e_{\mathbf{1}})) \cdot e_{K, S, V} = b e_{K, S, V}$
. Since it is proved in [
Reference Burns, Kurihara and Sano17
, Theorem 5·14] that one has
$\lambda^{(\ell)} \cdot e_{K, S, V} = (a e_{\mathbf{1}} + b ( 1 - e_{\mathbf{1}})) \cdot e_{K, S, V} = b e_{K, S, V}$
. Since it is proved in [
Reference Burns, Kurihara and Sano17
, Theorem 5·14] that one has
![]() $\Theta_{K / k, S}^V ( z_{K / k, S, T}) = \varepsilon^V_{K / k, S, T}$
, we therefore deduce that
$\Theta_{K / k, S}^V ( z_{K / k, S, T}) = \varepsilon^V_{K / k, S, T}$
, we therefore deduce that
for each prime
![]() $\ell$
. Now, the equality
$\ell$
. Now, the equality
that is established via the argument of [ Reference Burns, Kurihara and Sano17 , Theorem 7·5] combines with the last displayed equation and the fact that b is invertible to imply that
The claim in Theorem 1·3 (i) now follows upon recalling that
![]() $\ell$
is an arbitrary prime number.
$\ell$
is an arbitrary prime number.
3·2. The proof in case (ii)
To prove Theorem 1·3 in case (ii), we let
![]() $K/k$
be a biquadratic extension of number fields and note that, by the known validity of Stark’s conjecture for
$K/k$
be a biquadratic extension of number fields and note that, by the known validity of Stark’s conjecture for
![]() $K / k$
, the zeta element
$K / k$
, the zeta element
![]() $z_{K / k, S, T}$
is a
$z_{K / k, S, T}$
is a
![]() ${\mathbb{Q}} [G]$
-basis of the free rank-one
${\mathbb{Q}} [G]$
-basis of the free rank-one
![]() ${\mathbb{Q}} [G]$
-module
${\mathbb{Q}} [G]$
-module
![]() ${\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
(cf. the argument of Lemma 3·1 (a)). We then let
${\mathbb{Q}} \otimes_{\mathbb{Z}} {\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
(cf. the argument of Lemma 3·1 (a)). We then let
![]() $\ell$
be an arbitrary prime number and choose, using Roiter’s Lemma, an element
$\ell$
be an arbitrary prime number and choose, using Roiter’s Lemma, an element
![]() $\mathfrak{z}_{K / k, S, T}^{(\ell)}$
that generates a
$\mathfrak{z}_{K / k, S, T}^{(\ell)}$
that generates a
![]() ${\mathbb{Z}} [G]$
-submodule of
${\mathbb{Z}} [G]$
-submodule of
![]() ${\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
of finite, prime-to-
${\mathrm{Det}}_{{\mathbb{Z}} [G]} ( C^\bullet_{K, S, T})$
of finite, prime-to-
![]() $\ell$
index. Label the proper intermediate fields of
$\ell$
index. Label the proper intermediate fields of
![]() $K / k$
as
$K / k$
as
![]() $K_1 \,{:\!=}\, k, K_2, K_3$
, and
$K_1 \,{:\!=}\, k, K_2, K_3$
, and
![]() $K_4$
, and, using Lemma 2·3 (iii), denote the image of
$K_4$
, and, using Lemma 2·3 (iii), denote the image of
![]() $\mathfrak{z}_{K / k, S, T}^{(\ell)}$
under the natural map
$\mathfrak{z}_{K / k, S, T}^{(\ell)}$
under the natural map
as
![]() $\mathfrak{z}_{K_i / k, S, T}^{(\ell)}$
for every
$\mathfrak{z}_{K_i / k, S, T}^{(\ell)}$
for every
![]() $i \in \{1, \dots, 4 \}$
. Write
$i \in \{1, \dots, 4 \}$
. Write
![]() $\chi_i$
for the trivial character if
$\chi_i$
for the trivial character if
![]() $i = 1$
and the non-trivial character of
$i = 1$
and the non-trivial character of
![]() $\mathrm{Gal}({K_i}/{k})$
otherwise. The discussion above (in case (i)) then shows that we have
$\mathrm{Gal}({K_i}/{k})$
otherwise. The discussion above (in case (i)) then shows that we have
for some
![]() $a_i$
in
$a_i$
in
![]() ${\mathbb{Z}}_{(\ell)}^\times$
. It follows that
${\mathbb{Z}}_{(\ell)}^\times$
. It follows that
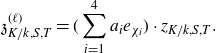 \[\mathfrak{z}_{K / k, S, T}^{(\ell)} =( \sum_{i = 1}^4 a_i e_{\chi_i}) \cdot z_{K / k, S, T}.\]
\[\mathfrak{z}_{K / k, S, T}^{(\ell)} =( \sum_{i = 1}^4 a_i e_{\chi_i}) \cdot z_{K / k, S, T}.\]
If
![]() $\ell \neq 2$
, then it is clear that
$\ell \neq 2$
, then it is clear that
![]() $\lambda^{(\ell)} \,{:\!=}\, \sum_{i = 1}^4 a_i e_{\chi_i}$
belongs to
$\lambda^{(\ell)} \,{:\!=}\, \sum_{i = 1}^4 a_i e_{\chi_i}$
belongs to
![]() ${\mathbb{Z}}_{(\ell)} [G]^\times$
. For
${\mathbb{Z}}_{(\ell)} [G]^\times$
. For
![]() $\ell = 2$
, the scalar
$\ell = 2$
, the scalar
![]() $\lambda^{(2)}$
belongs to
$\lambda^{(2)}$
belongs to
![]() ${\mathbb{Z}}_{(2)} [G]^\times$
if and only if it belongs to
${\mathbb{Z}}_{(2)} [G]^\times$
if and only if it belongs to
![]() ${\mathbb{Z}}_{(2)} [G]$
because
${\mathbb{Z}}_{(2)} [G]$
because
![]() $\mathrm{N}_{{\mathbb{Q}} [G] / {\mathbb{Q}}} (\lambda^{(2)}) = \prod_{i = 1}^4 a_i$
is a unit in
$\mathrm{N}_{{\mathbb{Q}} [G] / {\mathbb{Q}}} (\lambda^{(2)}) = \prod_{i = 1}^4 a_i$
is a unit in
![]() ${\mathbb{Z}}_{(2)}$
. Now,
${\mathbb{Z}}_{(2)}$
. Now,
![]() $\lambda^{(2)}$
is in
$\lambda^{(2)}$
is in
![]() ${\mathbb{Z}}_{(2)} [G]$
if and only if, for every
${\mathbb{Z}}_{(2)} [G]$
if and only if, for every
![]() $\sigma \in G$
we have that
$\sigma \in G$
we have that
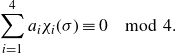 \[\sum_{i = 1}^4 a_i \chi_i (\sigma) \equiv 0 \mod 4.\]
\[\sum_{i = 1}^4 a_i \chi_i (\sigma) \equiv 0 \mod 4.\]
Note that
![]() $\chi_i (\sigma) = \pm 1$
and
$\chi_i (\sigma) = \pm 1$
and
![]() $a_i \equiv \pm 1 \mod 4$
for all
$a_i \equiv \pm 1 \mod 4$
for all
![]() $i \in \{1, \dots, 4\}$
. One can then check explicitly that the above congruence holds if and only if
$i \in \{1, \dots, 4\}$
. One can then check explicitly that the above congruence holds if and only if
![]() $\prod_{i = 1}^4 a_i \equiv 1 \mod 4$
(cf. also [
Reference Buckingham9
, Lemma 6·3 (v)]). In particular, if we let
$\prod_{i = 1}^4 a_i \equiv 1 \mod 4$
(cf. also [
Reference Buckingham9
, Lemma 6·3 (v)]). In particular, if we let
![]() $b \in \{ \pm 1 \}$
be defined by
$b \in \{ \pm 1 \}$
be defined by
![]() $b \equiv \prod_{i = 1}^4 a_i \mod 4$
, then
$b \equiv \prod_{i = 1}^4 a_i \mod 4$
, then
![]() $\lambda' \,{:\!=}\, b a_1 e_{\mathbf{1}} + \sum_{i = 1}^3 a_i e_{\chi_i}$
belongs to
$\lambda' \,{:\!=}\, b a_1 e_{\mathbf{1}} + \sum_{i = 1}^3 a_i e_{\chi_i}$
belongs to
![]() ${\mathbb{Z}}_{(2)} [G]^\times$
.
${\mathbb{Z}}_{(2)} [G]^\times$
.
As in case (i), we define
![]() $e_{K, S, V}$
as the sum of all
$e_{K, S, V}$
as the sum of all
![]() $e_\chi$
that annihilate
$e_\chi$
that annihilate
![]() ${\mathbb{C}} \otimes_{\mathbb{Z}} X_{K, S \setminus V}$
. The assumption
${\mathbb{C}} \otimes_{\mathbb{Z}} X_{K, S \setminus V}$
. The assumption
![]() $|S| \gt |V| + 1$
then ensures that
$|S| \gt |V| + 1$
then ensures that
![]() $e_{\mathbf{1}}\cdot e_{K, S, V}=0$
and thus that
$e_{\mathbf{1}}\cdot e_{K, S, V}=0$
and thus that
![]() $\lambda^{(2)} e_{K, S, V} = \lambda' e_{K, S, V}$
. Using the map
$\lambda^{(2)} e_{K, S, V} = \lambda' e_{K, S, V}$
. Using the map
![]() $\Theta^V_{K / k, S}$
defined in (3·4), we obtain the equality
$\Theta^V_{K / k, S}$
defined in (3·4), we obtain the equality
where the final equality follows from the argument of [
Reference Burns, Kurihara and Sano17
, Theorem 7·5] as in case (i). Since the corresponding identity also holds for each odd
![]() $\ell$
, this completes the proof of Theorem 1·3.
$\ell$
, this completes the proof of Theorem 1·3.
Remark 3·2. The only instances of (i) and (ii) in Theorem 1·3 that can neither be treated by the argument used to prove Theorem 1·3 nor Remark 1·11 (i) are the cases in which
![]() $|S| = |V| + 1$
and the unique place
$|S| = |V| + 1$
and the unique place
![]() $v \in S \setminus V$
has full decomposition group in
$v \in S \setminus V$
has full decomposition group in
![]() $K / k$
. In any such situation and for large enough V, the equality (1·3) is in fact equivalent to eTNC
$K / k$
. In any such situation and for large enough V, the equality (1·3) is in fact equivalent to eTNC
![]() $(K/k)$
and amounts to a subtle question about signs. To make this more explicit in case (ii) of Theorem 1·3, we suppose that
$(K/k)$
and amounts to a subtle question about signs. To make this more explicit in case (ii) of Theorem 1·3, we suppose that
![]() $K / k$
is biquadratic,
$K / k$
is biquadratic,
![]() $|S| = |V| + 1$
, and V is large enough that
$|S| = |V| + 1$
, and V is large enough that
![]() ${\mathrm{Cl}}_{K, S, T}$
vanishes. Then
${\mathrm{Cl}}_{K, S, T}$
vanishes. Then
![]() $\mathcal{O}_{K, S, T}^\times$
is a free
$\mathcal{O}_{K, S, T}^\times$
is a free
![]() ${\mathbb{Z}} [G]$
-module of rank
${\mathbb{Z}} [G]$
-module of rank
![]() $|V|$
and we can choose an ordered
$|V|$
and we can choose an ordered
![]() ${\mathbb{Z}} [G]$
-basis
${\mathbb{Z}} [G]$
-basis
![]() $\mathfrak{B}$
of
$\mathfrak{B}$
of
![]() $\mathcal{O}_{K, S, T}^\times$
. Fix an ordering
$\mathcal{O}_{K, S, T}^\times$
. Fix an ordering
![]() $G = \{ g_1, g_2, g_3, g_4 \}$
and consider the ordered
$G = \{ g_1, g_2, g_3, g_4 \}$
and consider the ordered
![]() ${\mathbb{Z}}$
-basis
${\mathbb{Z}}$
-basis
![]() $\mathfrak{B}' \,{:\!=}\, \{ g b \mid g \in G, b \in \mathfrak{B}\}$
of
$\mathfrak{B}' \,{:\!=}\, \{ g b \mid g \in G, b \in \mathfrak{B}\}$
of
![]() $\mathcal{O}_{K, S, T}^\times$
, ordered lexicographically. Similarly, we set
$\mathcal{O}_{K, S, T}^\times$
, ordered lexicographically. Similarly, we set
![]() $\mathfrak{W} \,{:\!=}\, \{ g w_i \mid g \in G, 1 \leq i \leq |V| \}$
, ordered lexicographically. Then one can show that (1·3) is equivalent to
$\mathfrak{W} \,{:\!=}\, \{ g w_i \mid g \in G, 1 \leq i \leq |V| \}$
, ordered lexicographically. Then one can show that (1·3) is equivalent to
(Cf. [
Reference Buckingham9
, Proposition 10·5].) This question does not depend on the ordering on G and, since G is
![]() ${\mathbb{Z}} / 2 {\mathbb{Z}} \oplus {\mathbb{Z}} / 2 {\mathbb{Z}}$
, also not on the choice of basis
${\mathbb{Z}} / 2 {\mathbb{Z}} \oplus {\mathbb{Z}} / 2 {\mathbb{Z}}$
, also not on the choice of basis
![]() $\mathfrak{B}$
(or the ordering on it) because every unit in
$\mathfrak{B}$
(or the ordering on it) because every unit in
![]() ${\mathbb{Z}} [G]$
is of the form
${\mathbb{Z}} [G]$
is of the form
![]() $\pm g$
for some
$\pm g$
for some
![]() $g \in G$
, and so has norm 1.
$g \in G$
, and so has norm 1.
In the setting of case (i) of Theorem 1·3 one can similarly derive an explicit criterion by using [ Reference Breuning6 , Lemma 3·5].
4. The proof of Theorem 1·1
We now fix a p-elementary extension
![]() $K/k$
with Galois group
$K/k$
with Galois group
![]() $G \cong ({\mathbb{Z} / {p} \mathbb{Z}})^m$
. Write
$G \cong ({\mathbb{Z} / {p} \mathbb{Z}})^m$
. Write
![]() $\Omega^\ast$
for the set of subgroups H of G of index at most p. The following algebraic observation plays a key role in the sequel.
$\Omega^\ast$
for the set of subgroups H of G of index at most p. The following algebraic observation plays a key role in the sequel.
Lemma 4·1. Set
![]() $\mathrm{N}_H = \sum_{\tau \in H} \tau$
for every
$\mathrm{N}_H = \sum_{\tau \in H} \tau$
for every
![]() $H \in \Omega^\ast$
. In
$H \in \Omega^\ast$
. In
![]() ${\mathbb{Z}} [G]$
we then have the equality
${\mathbb{Z}} [G]$
we then have the equality
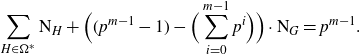 \[\sum_{H \in \Omega^\ast} \mathrm{N}_H + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big)\Big) \cdot \mathrm{N}_G = p^{m - 1}.\]
\[\sum_{H \in \Omega^\ast} \mathrm{N}_H + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big)\Big) \cdot \mathrm{N}_G = p^{m - 1}.\]
Proof. Observe that G is an
![]() $\mathbb{F}_p$
-vector space and the (non-trivial) H are exactly the
$\mathbb{F}_p$
-vector space and the (non-trivial) H are exactly the
![]() $(m - 1)$
-dimensional subspaces of G. Recall that the trace pairing
$(m - 1)$
-dimensional subspaces of G. Recall that the trace pairing
is perfect, hence induces a bijection between
![]() $(m - 1)$
-dimensional and 1-dimensional subspaces. The number of 1-dimensional subspaces is exactly
$(m - 1)$
-dimensional and 1-dimensional subspaces. The number of 1-dimensional subspaces is exactly
![]() ${p^{m} - 1}/{p - 1}$
, hence
${p^{m} - 1}/{p - 1}$
, hence
![]() $| \Omega^\ast \setminus \{ G \} |$
is equal to
$| \Omega^\ast \setminus \{ G \} |$
is equal to
![]() $ {p^{m} - 1}/{p - 1}$
. If we fix
$ {p^{m} - 1}/{p - 1}$
. If we fix
![]() $v \in \mathbb{F}_p \setminus \{ 0 \}$
, then the set of all
$v \in \mathbb{F}_p \setminus \{ 0 \}$
, then the set of all
![]() $(m - 1)$
-dimensional subspaces of
$(m - 1)$
-dimensional subspaces of
![]() $\mathbb{F}_p^m$
that contain v is in bijection with all 1-dimensional subspaces of the space
$\mathbb{F}_p^m$
that contain v is in bijection with all 1-dimensional subspaces of the space
![]() $\{ w \in \mathbb{F}_p^m \mid \sum_{i = 1}^m v_i w_i = 0 \}$
, the kernel of the
$\{ w \in \mathbb{F}_p^m \mid \sum_{i = 1}^m v_i w_i = 0 \}$
, the kernel of the
![]() $(1 \times m)$
-matrix v. This space is therefore of dimension
$(1 \times m)$
-matrix v. This space is therefore of dimension
![]() $m - 1$
and contains
$m - 1$
and contains
![]() ${p^{m - 1} - 1}/{p - 1}$
subspaces of dimension one. That is, there are exactly
${p^{m - 1} - 1}/{p - 1}$
subspaces of dimension one. That is, there are exactly
![]() ${p^{m - 1} - 1}/{p - 1}$
subgroups
${p^{m - 1} - 1}/{p - 1}$
subgroups
![]() $H \in \Omega^\ast \setminus \{ H \}$
that contain a given (non-trivial) element of G. It follows that there are exactly
$H \in \Omega^\ast \setminus \{ H \}$
that contain a given (non-trivial) element of G. It follows that there are exactly
such H that do not contain a given (non-trivial) element. Thus, each element of G appears in the sum
![]() $( \sum_{H \in \Omega^\ast \setminus \{ G \}} \mathrm{N}_H \Big) + p^{m - 1} ( N_G - 1)$
exactly
$( \sum_{H \in \Omega^\ast \setminus \{ G \}} \mathrm{N}_H \Big) + p^{m - 1} ( N_G - 1)$
exactly
![]() $| \Omega^\ast \setminus \{ G \} |$
many times. From this we obtain
$| \Omega^\ast \setminus \{ G \} |$
many times. From this we obtain
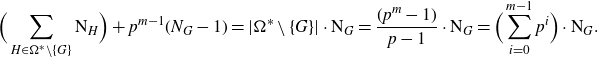 \begin{align*}\Big ( \sum_{H \in \Omega^\ast \setminus \{ G \}} \mathrm{N}_H \Big) + p^{m - 1} ( N_G - 1) &= | \Omega^\ast \setminus \{ G \} | \cdot \mathrm{N}_G = \frac{(p^{m} - 1)}{p - 1} \cdot \mathrm{N}_G = \Big ( \sum_{i = 0}^{m - 1} p^i \Big) \cdot \mathrm{N}_G. \end{align*}
\begin{align*}\Big ( \sum_{H \in \Omega^\ast \setminus \{ G \}} \mathrm{N}_H \Big) + p^{m - 1} ( N_G - 1) &= | \Omega^\ast \setminus \{ G \} | \cdot \mathrm{N}_G = \frac{(p^{m} - 1)}{p - 1} \cdot \mathrm{N}_G = \Big ( \sum_{i = 0}^{m - 1} p^i \Big) \cdot \mathrm{N}_G. \end{align*}
For any integer
![]() $r \geq 0$
and
$r \geq 0$
and
![]() $H\in\Omega^\ast$
, we consider the injection
$H\in\Omega^\ast$
, we consider the injection
that satisfies
As a straightforward application of Lemma 4·1 we obtain the following consequence that recovers [
Reference Sands51
, Proposition 4·5] in the case
![]() $p = 2$
.
$p = 2$
.
Proposition 4·2. In
![]() ${\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^r_{{\mathbb{Z}} [G]} {\mathcal{O}}_{K, S, T}^\times$
we have the equality
${\mathbb{R}} \otimes_{\mathbb{Z}} \bigwedge\nolimits^r_{{\mathbb{Z}} [G]} {\mathcal{O}}_{K, S, T}^\times$
we have the equality
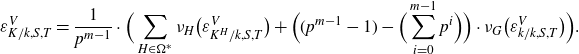 \[\varepsilon^V_{K / k, S, T} = \frac{1}{p^{m - 1}} \cdot \Big ( \sum_{H \in \Omega^\ast} \nu_H \big( \varepsilon_{K^H / k, S, T}^V \big) + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big) \Big) \cdot \nu_G \big ( \varepsilon_{k / k, S, T}^V \big) \Big).\]
\[\varepsilon^V_{K / k, S, T} = \frac{1}{p^{m - 1}} \cdot \Big ( \sum_{H \in \Omega^\ast} \nu_H \big( \varepsilon_{K^H / k, S, T}^V \big) + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big) \Big) \cdot \nu_G \big ( \varepsilon_{k / k, S, T}^V \big) \Big).\]
Proof. Using Lemma 4·1 (a), equation (4·5), and the norm relations for Rubin–Stark elements [ Reference Rubin48 , Proposition 6·1] we calculate
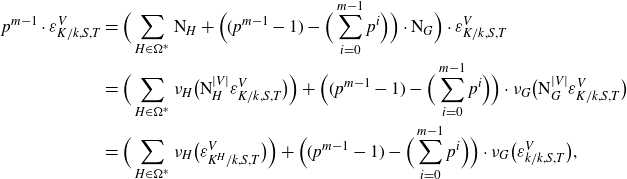 \begin{align*}p^{m - 1} \cdot \varepsilon_{K / k, S, T}^V & = \Big ( \sum_{H \in \Omega^\ast} \mathrm{N}_H + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big)\Big) \cdot \mathrm{N}_G \Big) \cdot \varepsilon_{K / k, S, T}^V \\& = \Big ( \sum_{H \in \Omega^\ast} \nu_H \big ( \mathrm{N}_H^{|V|} \varepsilon_{K / k, S, T}^V\big) \Big) + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big) \Big) \cdot \nu_G \big (\mathrm{N}_G^{|V|} \varepsilon_{K / k, S, T}^V\big) \\& = \Big ( \sum_{H \in \Omega^\ast} \nu_H \big ( \varepsilon_{K^H / k, S, T}^V \big) \Big) + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big) \Big) \cdot \nu_G \big (\varepsilon_{k / k, S, T}^V \big),\end{align*}
\begin{align*}p^{m - 1} \cdot \varepsilon_{K / k, S, T}^V & = \Big ( \sum_{H \in \Omega^\ast} \mathrm{N}_H + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big)\Big) \cdot \mathrm{N}_G \Big) \cdot \varepsilon_{K / k, S, T}^V \\& = \Big ( \sum_{H \in \Omega^\ast} \nu_H \big ( \mathrm{N}_H^{|V|} \varepsilon_{K / k, S, T}^V\big) \Big) + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big) \Big) \cdot \nu_G \big (\mathrm{N}_G^{|V|} \varepsilon_{K / k, S, T}^V\big) \\& = \Big ( \sum_{H \in \Omega^\ast} \nu_H \big ( \varepsilon_{K^H / k, S, T}^V \big) \Big) + \Big ( (p^{m - 1} - 1) - \Big (\sum_{i = 0}^{m - 1} p^i \Big) \Big) \cdot \nu_G \big (\varepsilon_{k / k, S, T}^V \big),\end{align*}
as required to prove the claim.
To prepare for the proof of Theorem 1·1, we now first give a preliminary result in which we write
![]() $I_G \,{:\!=}\, \ker \{ {\mathbb{Z}} [G] \to {\mathbb{Z}} \}$
for the absolute augmentation ideal of
$I_G \,{:\!=}\, \ker \{ {\mathbb{Z}} [G] \to {\mathbb{Z}} \}$
for the absolute augmentation ideal of
![]() ${\mathbb{Z}} [G]$
and, given a
${\mathbb{Z}} [G]$
and, given a
![]() ${\mathbb{Z}} [G]$
-module M and non-negative integer r, define its
${\mathbb{Z}} [G]$
-module M and non-negative integer r, define its
![]() $r$
-
th exterior bidual’ to be
$r$
-
th exterior bidual’ to be
Lemma 4·3. Fix a Rubin datum (S, V, T) for
![]() $K / k$
and a non-negative integer c that satisfies
$K / k$
and a non-negative integer c that satisfies
where
![]() $s_p \,{:\!=}\, \dim_{\mathbb{F}_p} ({\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p)$
denotes the p-rank of
$s_p \,{:\!=}\, \dim_{\mathbb{F}_p} ({\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p)$
denotes the p-rank of
![]() ${\mathrm{Cl}}_{k, S, T}$
. If the equality (1·3) of Conjecture 1·10 holds for all extensions
${\mathrm{Cl}}_{k, S, T}$
. If the equality (1·3) of Conjecture 1·10 holds for all extensions
![]() $L / k$
in
$L / k$
in
![]() $\Omega$
, then
$\Omega$
, then
![]() $\varepsilon^V_{K / k, S, T}$
belongs to
$\varepsilon^V_{K / k, S, T}$
belongs to
![]() $I_G^c \cdot \bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times$
(so, in particular, the Rubin–Stark conjecture is valid for
$I_G^c \cdot \bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times$
(so, in particular, the Rubin–Stark conjecture is valid for
![]() $(K/k,S,V,T)$
).
$(K/k,S,V,T)$
).
Proof. At the outset we note that, for any
![]() $H \in \Omega^\ast$
, the map
$H \in \Omega^\ast$
, the map
![]() $\nu_H$
restricts to an injection
$\nu_H$
restricts to an injection
![]() $\bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathcal{O}_{K^H, S, T}^\times \to \bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times$
(cf. [
Reference Burns, Kurihara and Sano17
, Remark 4·13]). By Proposition 4·2, it is hence sufficient to prove that
$\bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathcal{O}_{K^H, S, T}^\times \to \bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times$
(cf. [
Reference Burns, Kurihara and Sano17
, Remark 4·13]). By Proposition 4·2, it is hence sufficient to prove that
![]() $\varepsilon^V_{K^H / k, S, T}$
belongs to
$\varepsilon^V_{K^H / k, S, T}$
belongs to
![]() $p^{m - 1} I_{G / H}^c \bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathcal{O}_{K^H, S, T}^\times$
for every
$p^{m - 1} I_{G / H}^c \bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathcal{O}_{K^H, S, T}^\times$
for every
![]() $H \in \Omega^\ast$
. By the assumption
$H \in \Omega^\ast$
. By the assumption
![]() $|S| \geq |V| + 2$
, we may and will assume
$|S| \geq |V| + 2$
, we may and will assume
![]() $K^H \neq k$
so that
$K^H \neq k$
so that
![]() $K^H \in \Omega$
.
$K^H \in \Omega$
.
We now first claim that for this purpose it is enough to prove that
![]() $\mathrm{im} (\varepsilon^V_{K^H / k, S, T})$
is contained in
$\mathrm{im} (\varepsilon^V_{K^H / k, S, T})$
is contained in
![]() $p^{m - 1} I_{G / H}^{ 1 + c}$
. To justify this, we apply Lemma 2·3 (ii) to fix a representative
$p^{m - 1} I_{G / H}^{ 1 + c}$
. To justify this, we apply Lemma 2·3 (ii) to fix a representative
![]() $[P_0 \stackrel{\phi}{\to} P_1]$
of the complex
$[P_0 \stackrel{\phi}{\to} P_1]$
of the complex
![]() $C^\bullet_{K^H, S, T}$
in
$C^\bullet_{K^H, S, T}$
in
![]() $D^{\mathrm{p}}(\mathbb{Z}[G/H])$
. From [
Reference Sakamoto49
, Lemma B·6] we then obtain an exact sequence
$D^{\mathrm{p}}(\mathbb{Z}[G/H])$
. From [
Reference Sakamoto49
, Lemma B·6] we then obtain an exact sequence
In particular, we may view
![]() $\varepsilon^{V}_{K^H / k, S, T}$
as an element of
$\varepsilon^{V}_{K^H / k, S, T}$
as an element of
![]() $\bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} P_0$
. Now, if
$\bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} P_0$
. Now, if
![]() $\mathrm{im} (\varepsilon^V_{K^H / k, S, T})$
, which equals
$\mathrm{im} (\varepsilon^V_{K^H / k, S, T})$
, which equals
![]() $ \{F ( \varepsilon^{V}_{K^H / k, S, T}) \mid F \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathrm{Hom}_{{\mathbb{Z}} [G]}(P_0, {\mathbb{Z}} [G]) \}$
, is contained in
$ \{F ( \varepsilon^{V}_{K^H / k, S, T}) \mid F \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathrm{Hom}_{{\mathbb{Z}} [G]}(P_0, {\mathbb{Z}} [G]) \}$
, is contained in
![]() $p^{m - 1} I_{G / H}^{1 + c}$
, then
$p^{m - 1} I_{G / H}^{1 + c}$
, then
![]() $\varepsilon^{V}_{K^H / k, S, T}$
belongs to the module
$\varepsilon^{V}_{K^H / k, S, T}$
belongs to the module
![]() $p^{ m - 1} I_{G / H}^{1 + c} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} P_0$
(cf. [
Reference Burns, Kurihara and Sano17
, Proposition 4·17]). We may therefore write
$p^{ m - 1} I_{G / H}^{1 + c} \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} P_0$
(cf. [
Reference Burns, Kurihara and Sano17
, Proposition 4·17]). We may therefore write
![]() $\varepsilon^{V}_{K^H / k, S, T} = p^{m - 1} (\sigma_H - 1)^{ 1 + c} a$
with
$\varepsilon^{V}_{K^H / k, S, T} = p^{m - 1} (\sigma_H - 1)^{ 1 + c} a$
with
![]() $\sigma_H$
a generator of
$\sigma_H$
a generator of
![]() $G / H$
and a an element of
$G / H$
and a an element of
![]() $\bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} P_0$
. From the exact sequence (4·6) we then see that
$\bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} P_0$
. From the exact sequence (4·6) we then see that
Since
![]() $P' \,{:\!=}\, P_1 \otimes_{{\mathbb{Z}} [G / H]} \bigwedge\nolimits^{|V| - 1}_{{\mathbb{Z}} [G/ H]} P_0$
is
$P' \,{:\!=}\, P_1 \otimes_{{\mathbb{Z}} [G / H]} \bigwedge\nolimits^{|V| - 1}_{{\mathbb{Z}} [G/ H]} P_0$
is
![]() ${\mathbb{Z}}$
-torsion free, this implies that
${\mathbb{Z}}$
-torsion free, this implies that
![]() $(\sigma_H - 1)^{1 + c} \cdot \phi (a)$
vanishes. As
$(\sigma_H - 1)^{1 + c} \cdot \phi (a)$
vanishes. As
![]() $(\sigma_H - 1)P'$
and
$(\sigma_H - 1)P'$
and
![]() $(P')^{G / H} = \ker \{ P' \stackrel{\cdot(\sigma_H - 1)}{\longrightarrow} P' \}$
intersect trivially because P’ is
$(P')^{G / H} = \ker \{ P' \stackrel{\cdot(\sigma_H - 1)}{\longrightarrow} P' \}$
intersect trivially because P’ is
![]() $G/H$
-cohomologically trivial, it then follows by induction on c that
$G/H$
-cohomologically trivial, it then follows by induction on c that
![]() $(\sigma_H - 1) \phi (a)$
vanishes. Exactness of (4·6) now shows that
$(\sigma_H - 1) \phi (a)$
vanishes. Exactness of (4·6) now shows that
![]() $(\sigma_H - 1) a$
belongs to
$(\sigma_H - 1) a$
belongs to
![]() $\bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathcal{O}_{K^H, S, T}^\times$
, as required to prove that
$\bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathcal{O}_{K^H, S, T}^\times$
, as required to prove that
![]() $\varepsilon^V_{K^H, S, T}$
belongs to
$\varepsilon^V_{K^H, S, T}$
belongs to
![]() $p^{m - 1} (\sigma_H - 1)^c \bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathcal{O}_{K^H, S, T}^\times$
.
$p^{m - 1} (\sigma_H - 1)^c \bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G / H]} \mathcal{O}_{K^H, S, T}^\times$
.
It now remains to prove that
![]() $\mathrm{im} (\varepsilon^V_{K^H / k, S, T})$
is contained in
$\mathrm{im} (\varepsilon^V_{K^H / k, S, T})$
is contained in
![]() $p^{m - 1} I_{G / H}^{1 + c}$
. We may and will assume that no place in
$p^{m - 1} I_{G / H}^{1 + c}$
. We may and will assume that no place in
![]() $S \setminus V$
splits completely in
$S \setminus V$
splits completely in
![]() $K^H / k$
, since otherwise
$K^H / k$
, since otherwise
![]() $\varepsilon_{K^H / k, S, T}^V$
vanishes. Thus, every place in
$\varepsilon_{K^H / k, S, T}^V$
vanishes. Thus, every place in
![]() $S \setminus V$
has full decomposition group in
$S \setminus V$
has full decomposition group in
![]() $K^H / k$
. Since we assume (1·3) to hold for
$K^H / k$
. Since we assume (1·3) to hold for
![]() $K^H / k$
it is enough to prove, in this situation, that
$K^H / k$
it is enough to prove, in this situation, that
![]() ${\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} (\mathrm{Sel}_{K^H, S, T})^\#\subseteq p^{m - 1}I_{G / H}^{1 + c}$
.
${\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} (\mathrm{Sel}_{K^H, S, T})^\#\subseteq p^{m - 1}I_{G / H}^{1 + c}$
.
To verify this inclusion, we use the ‘transpose’ Selmer group defined in Lemma 2·3 (i) and the equality
of [
Reference Burns, Kurihara and Sano17
, Lemma 2·8]. It then suffices to verify that
![]() ${\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} ( \mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T})\subseteq p^{m - 1} I_{G / H}^{1+c}$
.
${\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} ( \mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T})\subseteq p^{m - 1} I_{G / H}^{1+c}$
.
For this purpose, we first note that
![]() $Y_{K^H, V}$
is a free direct summand of
$Y_{K^H, V}$
is a free direct summand of
![]() $X_{K^H,S}\cong Y_{K^H, V} \oplus X_{K^H, S\setminus V}$
, hence also of
$X_{K^H,S}\cong Y_{K^H, V} \oplus X_{K^H, S\setminus V}$
, hence also of
![]() $\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T}$
. We may thus find a
$\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T}$
. We may thus find a
![]() ${\mathbb{Z}} [G / H]$
-module M such that
${\mathbb{Z}} [G / H]$
-module M such that
![]() $\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T} \cong M \oplus Y_{K^H, V}$
and one has the following modified version of the exact sequence in Lemma 2·3 (i):
$\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T} \cong M \oplus Y_{K^H, V}$
and one has the following modified version of the exact sequence in Lemma 2·3 (i):
Setting
![]() $d \,{:\!=}\, | S \setminus V|$
, one has
$d \,{:\!=}\, | S \setminus V|$
, one has
![]() $X_{K^H, S \setminus V} \cong {\mathbb{Z}}^{d - 1}$
and fixing again a generator
$X_{K^H, S \setminus V} \cong {\mathbb{Z}}^{d - 1}$
and fixing again a generator
![]() $\sigma_H$
of
$\sigma_H$
of
![]() $G/H$
,
$G/H$
,
In particular,
![]() ${\operatorname{Fitt}}^0_{{\mathbb{Z}} [G / H]} ( X_{K^H, S \setminus V})$
is a principal ideal and so we may apply [
Reference Johnston and Nickel31
, Lemma 2·5 (ii)] to the exact sequence (4·7) to infer that
${\operatorname{Fitt}}^0_{{\mathbb{Z}} [G / H]} ( X_{K^H, S \setminus V})$
is a principal ideal and so we may apply [
Reference Johnston and Nickel31
, Lemma 2·5 (ii)] to the exact sequence (4·7) to infer that
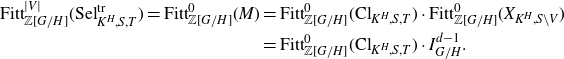 \begin{align*}{\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} (\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T})= {\operatorname{Fitt}}^{0}_{{\mathbb{Z}} [G / H]} (M) & = {\operatorname{Fitt}}^0_{{\mathbb{Z}} [G/ H]} ( {\mathrm{Cl}}_{K^H,S, T}) \cdot {\operatorname{Fitt}}^0_{{\mathbb{Z}} [G / H]} ( X_{K^H, S \setminus V}) \\& = {\operatorname{Fitt}}^0_{{\mathbb{Z}} [G/ H]} ( {\mathrm{Cl}}_{K^H,S, T}) \cdot I_{G / H}^{d - 1}.\end{align*}
\begin{align*}{\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} (\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T})= {\operatorname{Fitt}}^{0}_{{\mathbb{Z}} [G / H]} (M) & = {\operatorname{Fitt}}^0_{{\mathbb{Z}} [G/ H]} ( {\mathrm{Cl}}_{K^H,S, T}) \cdot {\operatorname{Fitt}}^0_{{\mathbb{Z}} [G / H]} ( X_{K^H, S \setminus V}) \\& = {\operatorname{Fitt}}^0_{{\mathbb{Z}} [G/ H]} ( {\mathrm{Cl}}_{K^H,S, T}) \cdot I_{G / H}^{d - 1}.\end{align*}
Fix a place
![]() $v \in S \setminus V$
and recall that we may assume that v has full decomposition group in
$v \in S \setminus V$
and recall that we may assume that v has full decomposition group in
![]() $K^H / k$
. If we write
$K^H / k$
. If we write
![]() $H_{S, T} (K^H)$
and
$H_{S, T} (K^H)$
and
![]() $H_{S, T} (k)$
for the (S, T)-ray class fields of
$H_{S, T} (k)$
for the (S, T)-ray class fields of
![]() $K^H$
and k, respectively, then
$K^H$
and k, respectively, then
![]() $H_{S, T} (k) \cap K^H = k$
since v splits completely in
$H_{S, T} (k) \cap K^H = k$
since v splits completely in
![]() $H_{S, T} (k)$
. Thus, we may identify
$H_{S, T} (k)$
. Thus, we may identify
![]() $\mathrm{Gal}({H_{S, T} (k)}/{k}) \cong \mathrm{Gal}({K^H \cdot H_{S, T} (k)}/{K^H})$
and hence the restriction map
$\mathrm{Gal}({H_{S, T} (k)}/{k}) \cong \mathrm{Gal}({K^H \cdot H_{S, T} (k)}/{K^H})$
and hence the restriction map
![]() $\mathrm{Gal}({H_{S, T} (K^H)}/{K^H}) \to \mathrm{Gal}({H_{S, T} (k)}/{k})$
is surjective. By class field theory, the restriction map corresponds to the norm map
$\mathrm{Gal}({H_{S, T} (K^H)}/{K^H}) \to \mathrm{Gal}({H_{S, T} (k)}/{k})$
is surjective. By class field theory, the restriction map corresponds to the norm map
![]() ${\mathrm{Cl}}_{K^H,S, T} \to {\mathrm{Cl}}_{k,S, T}$
and so, in particular, the map
${\mathrm{Cl}}_{K^H,S, T} \to {\mathrm{Cl}}_{k,S, T}$
and so, in particular, the map
![]() ${\mathrm{Cl}}_{K^H,S, T} \to {\mathrm{Cl}}_{k,S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p \cong ({\mathbb{Z} / {p} \mathbb{Z}})^{s_p}$
is surjective as well. This map is
${\mathrm{Cl}}_{K^H,S, T} \to {\mathrm{Cl}}_{k,S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p \cong ({\mathbb{Z} / {p} \mathbb{Z}})^{s_p}$
is surjective as well. This map is
![]() $G/ H$
-equivariant, thus we obtain an inclusion
$G/ H$
-equivariant, thus we obtain an inclusion
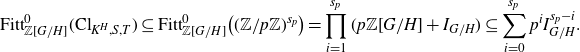 \[{\operatorname{Fitt}}^0_{{\mathbb{Z}}[G / H]} ( {\mathrm{Cl}}_{K^H,S, T}) \subseteq {\operatorname{Fitt}}^0_{{\mathbb{Z}} [G / H]} \big( ({\mathbb{Z}} /p {\mathbb{Z}})^{s_p} \big) = \prod_{i = 1}^{s_p} ( p {\mathbb{Z}} [G / H] + I_{G / H})\subseteq \sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i}.\]
\[{\operatorname{Fitt}}^0_{{\mathbb{Z}}[G / H]} ( {\mathrm{Cl}}_{K^H,S, T}) \subseteq {\operatorname{Fitt}}^0_{{\mathbb{Z}} [G / H]} \big( ({\mathbb{Z}} /p {\mathbb{Z}})^{s_p} \big) = \prod_{i = 1}^{s_p} ( p {\mathbb{Z}} [G / H] + I_{G / H})\subseteq \sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i}.\]
By the previous discussion, we therefore have an inclusion
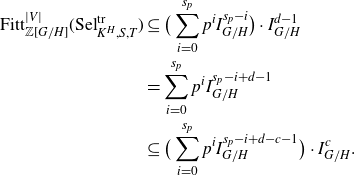 \begin{align*} {\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} (\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T})& \subseteq \big ( \sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i} \big) I_{G / H}^{d - 1} \\ &= \sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i + d - 1} \\&\subseteq \big ( \sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i + d - c - 1} \big) \cdot I_{G / H}^c.\end{align*}
\begin{align*} {\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} (\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T})& \subseteq \big ( \sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i} \big) I_{G / H}^{d - 1} \\ &= \sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i + d - 1} \\&\subseteq \big ( \sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i + d - c - 1} \big) \cdot I_{G / H}^c.\end{align*}
Since
![]() $\sigma_H$
is of order p, we have
$\sigma_H$
is of order p, we have
![]() $(\sigma_H - 1)^p \equiv \sigma_H^p - 1 = 0 \mod p$
and so
$(\sigma_H - 1)^p \equiv \sigma_H^p - 1 = 0 \mod p$
and so
![]() $(\sigma_H - 1)^p$
is divisible by p in
$(\sigma_H - 1)^p$
is divisible by p in
![]() ${\mathbb{Z}} [G / H]$
. Noting that the quotient
${\mathbb{Z}} [G / H]$
. Noting that the quotient
![]() ${\mathbb{Z}} [G / H] / I_{G / H} \cong {\mathbb{Z}}$
is torsion-free, we see that
${\mathbb{Z}} [G / H] / I_{G / H} \cong {\mathbb{Z}}$
is torsion-free, we see that
![]() $(\sigma_H - 1)^p$
is in fact divisible by
$(\sigma_H - 1)^p$
is in fact divisible by
![]() $p (\sigma_H - 1)$
. From this it follows that
$p (\sigma_H - 1)$
. From this it follows that
![]() $(\sigma_H - 1)^{s_p - i + d -c - 1}$
is divisible by
$(\sigma_H - 1)^{s_p - i + d -c - 1}$
is divisible by
![]() $p^{\max \{ 0, \lfloor (s_p - i + d - c - 2) / (p -1) \rfloor\}} (\sigma_H - 1)$
. As a consequence,
$p^{\max \{ 0, \lfloor (s_p - i + d - c - 2) / (p -1) \rfloor\}} (\sigma_H - 1)$
. As a consequence,
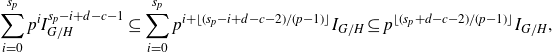 \[\sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i + d - c - 1}\subseteq\sum_{i = 0}^{s_p} p^{i + \lfloor (s_p - i + d - c - 2) / (p -1) \rfloor} I_{G / H}\subseteq p^{\lfloor (s_p + d - c - 2) / (p -1) \rfloor} I_{G / H},\]
\[\sum_{i = 0}^{s_p} p^i I_{G / H}^{s_p - i + d - c - 1}\subseteq\sum_{i = 0}^{s_p} p^{i + \lfloor (s_p - i + d - c - 2) / (p -1) \rfloor} I_{G / H}\subseteq p^{\lfloor (s_p + d - c - 2) / (p -1) \rfloor} I_{G / H},\]
where we have used that
as a consequence of
![]() $ p -1 \geq 1$
. Now,
$ p -1 \geq 1$
. Now,
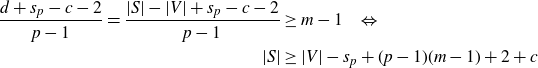 \begin{align*}\frac{d + s_p - c - 2}{p -1} =\frac{|S| - |V| + s_p - c - 2}{p -1} &\geq m - 1{\quad \Leftrightarrow \quad}\\|S|& \geq |V| - s_p + (p - 1) ( m - 1) + 2 + c\end{align*}
\begin{align*}\frac{d + s_p - c - 2}{p -1} =\frac{|S| - |V| + s_p - c - 2}{p -1} &\geq m - 1{\quad \Leftrightarrow \quad}\\|S|& \geq |V| - s_p + (p - 1) ( m - 1) + 2 + c\end{align*}
and so
![]() ${\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} (\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T})$
is contained in
${\operatorname{Fitt}}^{|V|}_{{\mathbb{Z}} [G / H]} (\mathrm{Sel}^{\mathrm{tr}}_{K^H, S, T})$
is contained in
![]() $p^{m - 1} I_{G / H}^{1 + c}$
as soon as
$p^{m - 1} I_{G / H}^{1 + c}$
as soon as
![]() $|S| \geq |V| - s_p + (p - 1) ( m - 1) + 2 + c$
. This concludes the proof that
$|S| \geq |V| - s_p + (p - 1) ( m - 1) + 2 + c$
. This concludes the proof that
![]() $\mathrm{im} (\varepsilon^V_{K / k, S, T})$
is contained in
$\mathrm{im} (\varepsilon^V_{K / k, S, T})$
is contained in
![]() $p^{m - 1} I_{G / H}^{1 + c}$
, as required.
$p^{m - 1} I_{G / H}^{1 + c}$
, as required.
We can now give the proof of Theorem 1·1.
Proof (of Theorem 1·1): Write
![]() $H_{k, p}$
and
$H_{k, p}$
and
![]() $H_K$
for the extensions of k and K that correspond with
$H_K$
for the extensions of k and K that correspond with
![]() ${\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p$
and
${\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p$
and
![]() ${\mathrm{Cl}}_{K, S, T}$
via class field theory. That is,
${\mathrm{Cl}}_{K, S, T}$
via class field theory. That is,
![]() $H_{k, p}$
is the maximal p-elementary abelian extension of k that is unramified outside T and in which all places in S split completely, and
$H_{k, p}$
is the maximal p-elementary abelian extension of k that is unramified outside T and in which all places in S split completely, and
![]() $H_K$
is the maximal abelian extension of K that is unramified outside
$H_K$
is the maximal abelian extension of K that is unramified outside
![]() $T_K$
and in which all places in
$T_K$
and in which all places in
![]() $S_K$
split completely. Note that
$S_K$
split completely. Note that
![]() $H_K$
is Galois over k. By Cebotarev’s density theorem, we may then choose a finite set W of prime ideals of k that has all of the following properties:
$H_K$
is Galois over k. By Cebotarev’s density theorem, we may then choose a finite set W of prime ideals of k that has all of the following properties:
-
(i) W is disjoint from
 $S \cup T$
;
$S \cup T$
; -
(ii) every place in W splits completely in
 $K \cdot H_{k, p}$
;
$K \cdot H_{k, p}$
; -
(iii)
 $\{ {\mathrm{Frob}}_{\mathfrak{p}} \mid {\mathfrak{p}} \in W \}$
is a generating set for
$\{ {\mathrm{Frob}}_{\mathfrak{p}} \mid {\mathfrak{p}} \in W \}$
is a generating set for
 $\mathrm{Gal}({H_K}/{ K \cdot H_{k, p}})$
.
$\mathrm{Gal}({H_K}/{ K \cdot H_{k, p}})$
.
In particular, one has
![]() ${\mathrm{Cl}}_{k, S', T} \otimes_{\mathbb{Z}} {\mathbb{Z}}_p = {\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p$
with
${\mathrm{Cl}}_{k, S', T} \otimes_{\mathbb{Z}} {\mathbb{Z}}_p = {\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p$
with
![]() $S' \,{:\!=}\, S \cup W$
. Class field theory then provides for a commutative diagram
$S' \,{:\!=}\, S \cup W$
. Class field theory then provides for a commutative diagram
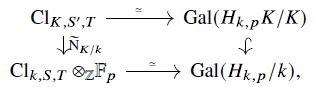
where the right-hand vertical arrow is the natural restriction map and
![]() $\widetilde{\mathrm{N}}_{K / k}$
is the composite of the ‘norm’ map
$\widetilde{\mathrm{N}}_{K / k}$
is the composite of the ‘norm’ map
![]() ${\mathrm{Cl}}_{K, S', T} \to {\mathrm{Cl}}_{k, S', T}$
induced by the norm
${\mathrm{Cl}}_{K, S', T} \to {\mathrm{Cl}}_{k, S', T}$
induced by the norm
![]() $\mathrm{N}_{K / k} {\colon} K^\times \to k^\times$
and the projection
$\mathrm{N}_{K / k} {\colon} K^\times \to k^\times$
and the projection
![]() $ {\mathrm{Cl}}_{k, S', T} \to {\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p$
. As a consequence, we obtain a G-equivariant isomorphism
$ {\mathrm{Cl}}_{k, S', T} \to {\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p$
. As a consequence, we obtain a G-equivariant isomorphism
![]() ${\mathrm{Cl}}_{K, S', T} \cong \widetilde{\mathrm{N}}_{K / k} ( {\mathrm{Cl}}_{K, S', T})$
, and hence an exact sequence of
${\mathrm{Cl}}_{K, S', T} \cong \widetilde{\mathrm{N}}_{K / k} ( {\mathrm{Cl}}_{K, S', T})$
, and hence an exact sequence of
![]() ${\mathbb{Z}} [G]$
-modules
${\mathbb{Z}} [G]$
-modules
with
![]() $\psi {\colon} \mathcal{O}_{K, S', T}^\times \to Y_{K, W}$
the map
$\psi {\colon} \mathcal{O}_{K, S', T}^\times \to Y_{K, W}$
the map
![]() $ a \mapsto \sum_{w \in W_K} {\mathrm{ord}}_w (a) w$
and
$ a \mapsto \sum_{w \in W_K} {\mathrm{ord}}_w (a) w$
and
![]() $\delta {\colon} Y_{K, W} \to {\mathrm{Cl}}_{K, S, T}$
sends
$\delta {\colon} Y_{K, W} \to {\mathrm{Cl}}_{K, S, T}$
sends
![]() $w \in W_K$
to the class of w in
$w \in W_K$
to the class of w in
![]() ${\mathrm{Cl}}_{K, S, T}$
.
${\mathrm{Cl}}_{K, S, T}$
.
Fix a labelling
![]() $W = \{ v_{|S| + 1}, \dots, v_{|S'|}\}$
and, for each
$W = \{ v_{|S| + 1}, \dots, v_{|S'|}\}$
and, for each
![]() $j \in \{ |S| + 1, \dots, |S'|\}$
, an extension
$j \in \{ |S| + 1, \dots, |S'|\}$
, an extension
![]() $w_j$
of
$w_j$
of
![]() $v_j$
to K. By condition (ii) every place of K above a fixed
$v_j$
to K. By condition (ii) every place of K above a fixed
![]() $v_j$
is of the form
$v_j$
is of the form
![]() $\sigma w_j$
for some
$\sigma w_j$
for some
![]() $\sigma \in G$
, which allows us to define a map
$\sigma \in G$
, which allows us to define a map
![]() $w_j^\ast {\colon} Y_{K, W} \to {\mathbb{Z}} [G]$
by sending
$w_j^\ast {\colon} Y_{K, W} \to {\mathbb{Z}} [G]$
by sending
![]() $\sum_{w \in W_K} a_w w$
to
$\sum_{w \in W_K} a_w w$
to
![]() $\sum_{\sigma \in G} a_{\sigma w} \sigma$
(so
$\sum_{\sigma \in G} a_{\sigma w} \sigma$
(so
![]() $w_j^\ast$
is the ‘dual’ of
$w_j^\ast$
is the ‘dual’ of
![]() $w_j$
). Now, if
$w_j$
). Now, if
![]() $a \in \mathcal{O}_{K, S_j, T}^\times$
with
$a \in \mathcal{O}_{K, S_j, T}^\times$
with
![]() $S_j \,{:\!=}\, S \cup \{ v_j \}$
, then
$S_j \,{:\!=}\, S \cup \{ v_j \}$
, then
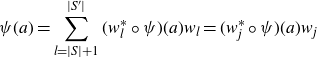 \[\psi (a) = \sum_{l = |S| + 1}^{|S'|} (w_l^\ast \circ \psi) (a) w_l = (w_j^\ast \circ \psi) (a) w_j\]
\[\psi (a) = \sum_{l = |S| + 1}^{|S'|} (w_l^\ast \circ \psi) (a) w_l = (w_j^\ast \circ \psi) (a) w_j\]
belongs to the kernel of
![]() $\delta$
by exactness of (4·8). This shows that
$\delta$
by exactness of (4·8). This shows that
![]() $(w_j^\ast \circ \psi) (a)$
annihilates the class of
$(w_j^\ast \circ \psi) (a)$
annihilates the class of
![]() $w_j$
in
$w_j$
in
![]() ${\mathrm{Cl}}_{K, S, T}$
. Since
${\mathrm{Cl}}_{K, S, T}$
. Since
![]() $A \,{:\!=}\, \ker \{ {\mathrm{Cl}}_{K, S, T} \to \widetilde{\mathrm{N}}_{K / k} ( {\mathrm{Cl}}_{K, S', T}) \}$
is generated over
$A \,{:\!=}\, \ker \{ {\mathrm{Cl}}_{K, S, T} \to \widetilde{\mathrm{N}}_{K / k} ( {\mathrm{Cl}}_{K, S', T}) \}$
is generated over
![]() ${\mathbb{Z}} [G]$
by
${\mathbb{Z}} [G]$
by
![]() $\delta (w_{|S| + 1}), \dots, \delta (w_{|S'|})$
by exactness of (4·9), we have thereby proved that
$\delta (w_{|S| + 1}), \dots, \delta (w_{|S'|})$
by exactness of (4·9), we have thereby proved that
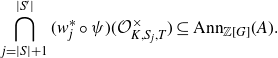 \begin{equation} \bigcap_{j = |S| + 1}^{|S'|} (w_j^\ast \circ \psi) ( \mathcal{O}_{K, S_j, T}^\times) \subseteq \mathrm{Ann}_{{\mathbb{Z}} [G]} (A).\end{equation}
\begin{equation} \bigcap_{j = |S| + 1}^{|S'|} (w_j^\ast \circ \psi) ( \mathcal{O}_{K, S_j, T}^\times) \subseteq \mathrm{Ann}_{{\mathbb{Z}} [G]} (A).\end{equation}
We now claim that
![]() $\mathrm{im} (\varepsilon^V_{K / k, S, T})$
is contained in
$\mathrm{im} (\varepsilon^V_{K / k, S, T})$
is contained in
![]() $I_G$
times the intersection on the left- hand side of (4·9). To do this, we first note that
$I_G$
times the intersection on the left- hand side of (4·9). To do this, we first note that
![]() $s'_p \,{:\!=}\, \dim_{\mathbb{F}_p} ( {\mathrm{Cl}}_{k, S', T} \otimes_{\mathbb{Z}} \mathbb{F}_p)$
is equal to
$s'_p \,{:\!=}\, \dim_{\mathbb{F}_p} ( {\mathrm{Cl}}_{k, S', T} \otimes_{\mathbb{Z}} \mathbb{F}_p)$
is equal to
![]() $s_p$
because
$s_p$
because
![]() ${\mathrm{Cl}}_{k, S', T} \otimes_{\mathbb{Z}} \mathbb{F}_p = {\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p$
by condition (ii). Setting
${\mathrm{Cl}}_{k, S', T} \otimes_{\mathbb{Z}} \mathbb{F}_p = {\mathrm{Cl}}_{k, S, T} \otimes_{\mathbb{Z}} \mathbb{F}_p$
by condition (ii). Setting
![]() $V' \,{:\!=}\, V \cup W$
, it then follows that
$V' \,{:\!=}\, V \cup W$
, it then follows that
By Lemma 4·3, we therefore have that
![]() $\varepsilon^{V'}_{K / k, S', T}$
belongs to
$\varepsilon^{V'}_{K / k, S', T}$
belongs to
![]() $I_G \cdot \bigcap\nolimits^{|V'|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S', T}^\times$
, hence can be written as
$I_G \cdot \bigcap\nolimits^{|V'|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S', T}^\times$
, hence can be written as
![]() $\varepsilon^{V'}_{K / k, S', T} = \sum_{i = 1}^t x_i a_i$
with a natural number t and elements
$\varepsilon^{V'}_{K / k, S', T} = \sum_{i = 1}^t x_i a_i$
with a natural number t and elements
![]() $x_1, \dots, x_t \in I_G$
and
$x_1, \dots, x_t \in I_G$
and
![]() $a_1, \dots, a_t \in \bigcap\nolimits^{|V'|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S', T}^\times$
.
$a_1, \dots, a_t \in \bigcap\nolimits^{|V'|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S', T}^\times$
.
At this stage, it is convenient to introduce some general notation. For a
![]() ${\mathbb{Z}} [G]$
-module M, we denote its
${\mathbb{Z}} [G]$
-module M, we denote its
![]() ${\mathbb{Z}} [G]$
-linear dual by
${\mathbb{Z}} [G]$
-linear dual by
![]() $M^\ast \,{:\!=}\, \mathrm{Hom}_{{\mathbb{Z}} [G]} ( M, {\mathbb{Z}} [G])$
. Given
$M^\ast \,{:\!=}\, \mathrm{Hom}_{{\mathbb{Z}} [G]} ( M, {\mathbb{Z}} [G])$
. Given
![]() $f \in M^\ast$
and an integer
$f \in M^\ast$
and an integer
![]() $r \geq 1$
, we then define a map
$r \geq 1$
, we then define a map
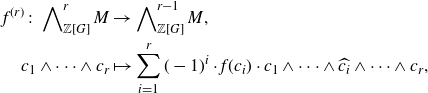 \begin{align*} f^{(r)} {\colon} \bigwedge\nolimits^r_{{\mathbb{Z}} [G]} M &\to \bigwedge\nolimits^{r - 1}_{{\mathbb{Z}} [G]} M, \\ c_1 \wedge \dots \wedge c_r &\mapsto \sum_{i = 1}^r (-1)^i \cdot f (c_i) \cdot c_1 \wedge \dots \wedge \widehat{c_i} \wedge \dots \wedge c_r,\end{align*}
\begin{align*} f^{(r)} {\colon} \bigwedge\nolimits^r_{{\mathbb{Z}} [G]} M &\to \bigwedge\nolimits^{r - 1}_{{\mathbb{Z}} [G]} M, \\ c_1 \wedge \dots \wedge c_r &\mapsto \sum_{i = 1}^r (-1)^i \cdot f (c_i) \cdot c_1 \wedge \dots \wedge \widehat{c_i} \wedge \dots \wedge c_r,\end{align*}
where the notation
![]() $\widehat{c_i}$
means omission of
$\widehat{c_i}$
means omission of
![]() $c_i$
. Iteration then yields a morphism
$c_i$
. Iteration then yields a morphism
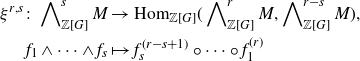 \begin{align*} \xi^{r, s} {\colon} \bigwedge\nolimits^s_{{\mathbb{Z}} [G]} M& \to \mathrm{Hom}_{{\mathbb{Z}} [G]} ( \bigwedge\nolimits^r_{{\mathbb{Z}} [G]} M, \bigwedge\nolimits^{r - s}_{{\mathbb{Z}} [G]} M),\\ f_1 \wedge \dots \wedge f_s &\mapsto f_s^{(r - s + 1)} \circ \dots \circ f_1^{(r)}\end{align*}
\begin{align*} \xi^{r, s} {\colon} \bigwedge\nolimits^s_{{\mathbb{Z}} [G]} M& \to \mathrm{Hom}_{{\mathbb{Z}} [G]} ( \bigwedge\nolimits^r_{{\mathbb{Z}} [G]} M, \bigwedge\nolimits^{r - s}_{{\mathbb{Z}} [G]} M),\\ f_1 \wedge \dots \wedge f_s &\mapsto f_s^{(r - s + 1)} \circ \dots \circ f_1^{(r)}\end{align*}
for every
![]() $s \leq r$
. (The special case
$s \leq r$
. (The special case
![]() $r = s$
of this construction was already discussed in Definition 2·1.) By abuse of notation we will simply write
$r = s$
of this construction was already discussed in Definition 2·1.) By abuse of notation we will simply write
![]() $f_1 \wedge \dots \wedge f_s$
in place of
$f_1 \wedge \dots \wedge f_s$
in place of
![]() $\xi^{r, s} (f_1 \wedge \dots \wedge f_s)$
.
$\xi^{r, s} (f_1 \wedge \dots \wedge f_s)$
.
Returning now to the concrete setting at hand, we set
![]() $\psi_l \,{:\!=}\, w_l^\ast \circ \psi$
and, for every
$\psi_l \,{:\!=}\, w_l^\ast \circ \psi$
and, for every
![]() $f \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} (\mathcal{O}_{K, S', T}^\times)^\ast$
and
$f \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} (\mathcal{O}_{K, S', T}^\times)^\ast$
and
![]() $j \in \{ |S| + 1, \dots, |S'| \}$
, define the map
$j \in \{ |S| + 1, \dots, |S'| \}$
, define the map
For every
![]() $g \in (\mathcal{O}_{K, S', T}^\times)^\ast$
and
$g \in (\mathcal{O}_{K, S', T}^\times)^\ast$
and
![]() $i\in \{1, \dots, t\}$
, one then has that
$i\in \{1, \dots, t\}$
, one then has that
![]() $(g \circ \Phi_{j, f}) ( a_i)$
belongs to
$(g \circ \Phi_{j, f}) ( a_i)$
belongs to
![]() ${\mathbb{Z}} [G]$
. This shows that
${\mathbb{Z}} [G]$
. This shows that
because
![]() $\mathcal{O}_{K, S', T}^\times$
is
$\mathcal{O}_{K, S', T}^\times$
is
![]() ${\mathbb{Z}}$
-torsion free. In addition,
${\mathbb{Z}}$
-torsion free. In addition,
![]() $\psi_l \circ \Phi_{j, f} = \Phi_{j, f} \wedge \psi_l = 0$
for all
$\psi_l \circ \Phi_{j, f} = \Phi_{j, f} \wedge \psi_l = 0$
for all
![]() $l \neq j$
so that in fact
$l \neq j$
so that in fact
![]() $\Phi_{j, f} (a_i) \in \bigcap_{l \neq j} \ker \psi_l = \mathcal{O}_{K, S_j, T}^\times$
. A similar argument also shows that
$\Phi_{j, f} (a_i) \in \bigcap_{l \neq j} \ker \psi_l = \mathcal{O}_{K, S_j, T}^\times$
. A similar argument also shows that
![]() $\big( \bigwedge\nolimits_{|S| + 1\leq l \leq |S'|} \psi_l \big) (a_i)$
belongs to
$\big( \bigwedge\nolimits_{|S| + 1\leq l \leq |S'|} \psi_l \big) (a_i)$
belongs to
![]() $\bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times$
.
$\bigcap\nolimits^{|V|}_{{\mathbb{Z}} [G]} \mathcal{O}_{K, S, T}^\times$
.
Note that
![]() $\mathcal{O}_{K, S', T}^\times / \mathcal{O}_{K, S, T}^\times$
is
$\mathcal{O}_{K, S', T}^\times / \mathcal{O}_{K, S, T}^\times$
is
![]() ${\mathbb{Z}}$
-torsion free (by (4·8)), hence that the natural restriction map
${\mathbb{Z}}$
-torsion free (by (4·8)), hence that the natural restriction map
![]() $\mathrm{res} {\colon} (\mathcal{O}_{K, S', T}^\times)^\ast \to (\mathcal{O}_{K, S, T}^\times)^\ast$
is surjective. For any
$\mathrm{res} {\colon} (\mathcal{O}_{K, S', T}^\times)^\ast \to (\mathcal{O}_{K, S, T}^\times)^\ast$
is surjective. For any
![]() $f \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} (\mathcal{O}_{K, S, T}^\times)^\ast$
we can therefore find
$f \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} (\mathcal{O}_{K, S, T}^\times)^\ast$
we can therefore find
![]() $\widetilde{f} \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} (\mathcal{O}_{K, S', T}^\times)^\ast$
with
$\widetilde{f} \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} (\mathcal{O}_{K, S', T}^\times)^\ast$
with
![]() $(\bigwedge^{|V|} \mathrm{res}) (\widetilde{f}) = f$
. For any
$(\bigwedge^{|V|} \mathrm{res}) (\widetilde{f}) = f$
. For any
![]() $j \in \{ |S| + 1, \dots, |S'| \}$
, we then obtain that
$j \in \{ |S| + 1, \dots, |S'| \}$
, we then obtain that
Since this inclusion holds for every such j, we infer that in fact
Now, by [ Reference Sano53 , Proposition 3·6] (see also [ Reference Rubin48 , Proposition 5·2]) one has
and so, for any
![]() $f \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} (\mathcal{O}_{K, S, T}^\times)^\ast$
, we deduce that
$f \in \bigwedge\nolimits^{|V|}_{{\mathbb{Z}} [G]} (\mathcal{O}_{K, S, T}^\times)^\ast$
, we deduce that
 \begin{align*} f ( \varepsilon^V_{K / k, S, T}) & = \pm \big( \big( \bigwedge\nolimits_{|S| + 1\leq l \leq |S'|} \psi_l \big) \wedge f \big) ( \varepsilon^{V'}_{K / k, S', T}) \\ & = \pm \sum_{i = 1}^t x_i \cdot \big( \big( \bigwedge\nolimits_{|S| + 1\leq l \leq |S'|} \psi_l \big) \wedge f \big) (a_i) \\ &\subseteq I_G \cdot {\bigcap}_{j = |S| + 1}^{|S'|} \psi_j ( \mathcal{O}_{K, S_j, T}^\times),\end{align*}
\begin{align*} f ( \varepsilon^V_{K / k, S, T}) & = \pm \big( \big( \bigwedge\nolimits_{|S| + 1\leq l \leq |S'|} \psi_l \big) \wedge f \big) ( \varepsilon^{V'}_{K / k, S', T}) \\ & = \pm \sum_{i = 1}^t x_i \cdot \big( \big( \bigwedge\nolimits_{|S| + 1\leq l \leq |S'|} \psi_l \big) \wedge f \big) (a_i) \\ &\subseteq I_G \cdot {\bigcap}_{j = |S| + 1}^{|S'|} \psi_j ( \mathcal{O}_{K, S_j, T}^\times),\end{align*}
as claimed. From (4·9), it now follows that
![]() $\mathrm{im} (\varepsilon^V_{K / k, S, T})$
is contained in
$\mathrm{im} (\varepsilon^V_{K / k, S, T})$
is contained in
![]() $I_G\cdot \mathrm{Ann}_{{\mathbb{Z}} [G]} (A)$
. As
$I_G\cdot \mathrm{Ann}_{{\mathbb{Z}} [G]} (A)$
. As
![]() $\widetilde{\mathrm{N}}_{K / k} ( {\mathrm{Cl}}_{K, S', T})$
(which carries the trivial G-action) is annihilated by
$\widetilde{\mathrm{N}}_{K / k} ( {\mathrm{Cl}}_{K, S', T})$
(which carries the trivial G-action) is annihilated by
![]() $I_G$
, we conclude from the tautological exact sequence
$I_G$
, we conclude from the tautological exact sequence
that any element in
![]() $\mathrm{im} (\varepsilon^V_{K / k, S, T})$
annihilates
$\mathrm{im} (\varepsilon^V_{K / k, S, T})$
annihilates
![]() ${\mathrm{Cl}}_{K, S, T}$
, as required to prove Theorem 1·1.
${\mathrm{Cl}}_{K, S, T}$
, as required to prove Theorem 1·1.
Acknowledgements
The authors would like to extend their gratitude to Werner Bley, David Burns and Andreas Nickel for helpful comments on an earlier version of this article. The first author moreover thanks Werner Bley for introducing him to the article [ Reference Rubin48 ] during a reading seminar at LMU Munich in 2018 and for asking the question to what degree [ Reference Rubin48 , Theorem 3·5] extends to extensions of degree p, which served as motivation for Theorem 1·3.
The first author wishes to acknowledge the financial support of the Engineering and Physical Sciences Research Council [EP/W522429/1, EP/W524335/1]. The second author acknowledges support for this article as part of Grants CEX2019-000904-S, PID2019-108936GB-C21 and PID2022-142024NB-I00 funded by MCIN/AEI/ 10.13039/501100011033.