Refine search
Actions for selected content:
237383 results in Physics and Astronomy
Centrifugal instability of Taylor–Couette flow in stratified and diffusive fluids
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 29 April 2025, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prediction of flow and polymeric stresses in a viscoelastic turbulent channel flow using convolutional neural networks
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Data-driven discovery of a heat flux closure for electrostatic plasma phenomena
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 28 April 2025, E64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vertical coherence of pressure and velocity structures in hypersonic turbulent boundary layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A11
-
- Article
- Export citation
Surface roughness effects on subsonic and supersonic turbulent boundary layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Physical aspects of Tollmien–Schlichting wave acoustic receptivity due to sharp-edged rectangular bumps and gaps investigated via subsonic high-fidelity simulations
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A59
-
- Article
- Export citation
Distribution of eigenfrequencies in long one-dimensional systems
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A9
-
- Article
- Export citation
Motion of a deformable droplet in a rectangular, straight channel
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ten-moment fluid modeling of the Weibel instability
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 28 April 2025, E66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small-scale anisotropy and ramp–cliff structures in turbulent shear flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, R6
-
- Article
- Export citation
Hypergraph removal with polynomial bounds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 321-330
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mechanisms underlying the generation and generalisation of the surface layer
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The main jet axis of the W49B supernova remnant
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 42 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e048
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Force balances in spherical shell rotating convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reversal of nonlinear energy transfer direction in flows over low-aspect-ratio plates
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A1
-
- Article
- Export citation
Mechanical power from thermocapillarity on superhydrophobic surfaces
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The radio re-brightening of the Type IIb SN 2001ig
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 42 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e050
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A depth-averaged model for granular flow consistent with the incompressible
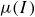 $\mu (I)$ rheology
$\mu (I)$ rheology
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A57
-
- Article
- Export citation
Experimental characterisation of Kelvin–Helmholtz rollers over riblet surfaces
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral dynamics and spatial structures of the conditional Lyapunov vector in slave Kolmogorov flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A12
-
- Article
- Export citation




































































 ) plates using the tomographic particle image velocimetry dataset originally obtained by Zhu
) plates using the tomographic particle image velocimetry dataset originally obtained by Zhu 




 plates.
plates.