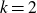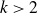1. Introduction
The hypergraph removal lemma is one of the most important results of extremal combinatorics. It states that for every fixed integer k, k-uniform hypergraph (k-graph for short) F and positive
![]() $\varepsilon$
, there is
$\varepsilon$
, there is
![]() $\delta=\delta(F,\varepsilon) \gt 0$
so that if G is an n-vertex k-graph with at least
$\delta=\delta(F,\varepsilon) \gt 0$
so that if G is an n-vertex k-graph with at least
![]() $\varepsilon n^k$
edge-disjointFootnote
1
copies of F, then G contains
$\varepsilon n^k$
edge-disjointFootnote
1
copies of F, then G contains
![]() $\delta n^{v(F)}$
copies of F. This lemma was first conjectured by Erdős, Frankl and Rödl [
Reference Erdős, Frankl and Rödl5
] as an alternative approach for proving Szemerédi’s theorem [
Reference Szemerédi15
]. The quest to proving this lemma, which involved the development of the hypergraph extension of Szemerédi’s regularity lemma [
Reference Szemerédi16
], took more than two decades, culminating in several proofs, first by Gowers [
Reference Gowers8
] and Rödl–Skokan–Nagle–Schacht [
Reference Nagle, Rödl and Schacht11, Reference Rödl and Skokan13
] and later by Tao [
Reference Tao17
]. For the sake of brevity, we refer the reader to [
Reference Rödl12
] for more background and references on the subject.
$\delta n^{v(F)}$
copies of F. This lemma was first conjectured by Erdős, Frankl and Rödl [
Reference Erdős, Frankl and Rödl5
] as an alternative approach for proving Szemerédi’s theorem [
Reference Szemerédi15
]. The quest to proving this lemma, which involved the development of the hypergraph extension of Szemerédi’s regularity lemma [
Reference Szemerédi16
], took more than two decades, culminating in several proofs, first by Gowers [
Reference Gowers8
] and Rödl–Skokan–Nagle–Schacht [
Reference Nagle, Rödl and Schacht11, Reference Rödl and Skokan13
] and later by Tao [
Reference Tao17
]. For the sake of brevity, we refer the reader to [
Reference Rödl12
] for more background and references on the subject.
While the hypergraph removal lemma has far-reaching qualitative applications, its main drawback is that it supplies very weak quantitative bounds. Specifically, for a general k-graph
![]() $F$
, the function
$F$
, the function
![]() $1/\delta(F,\varepsilon)$
grows like the
$1/\delta(F,\varepsilon)$
grows like the
![]() $k$
th Ackermann function. It is thus natural to ask for which k-graphs F one can obtain more sensible bounds. Further motivation for studying such questions comes from the area of graph property testing [
Reference Goldreich7
], where graph and hypergraph removal lemmas are used to design fast randomised algorithms.
$k$
th Ackermann function. It is thus natural to ask for which k-graphs F one can obtain more sensible bounds. Further motivation for studying such questions comes from the area of graph property testing [
Reference Goldreich7
], where graph and hypergraph removal lemmas are used to design fast randomised algorithms.
Suppose first that
![]() $k=2$
. In this case it is easy to see that if F is bipartite then
$k=2$
. In this case it is easy to see that if F is bipartite then
![]() $\delta(F,\varepsilon)$
grows polynomially with
$\delta(F,\varepsilon)$
grows polynomially with
![]() $\varepsilon$
. Indeed, if G has
$\varepsilon$
. Indeed, if G has
![]() $\varepsilon n^2$
edge-disjoint copies of F then it must have at least
$\varepsilon n^2$
edge-disjoint copies of F then it must have at least
![]() $\varepsilon n^2$
edges, which implies by the well-known Kővári–Sós–Turán theorem [
Reference Kővári, Sós and Turán10
], that G has at least
$\varepsilon n^2$
edges, which implies by the well-known Kővári–Sós–Turán theorem [
Reference Kővári, Sós and Turán10
], that G has at least
![]() $\mbox{poly}(\varepsilon)n^{v(F)}$
copies of F. In the seminal paper of Ruzsa and Szemerédi [
Reference Ruzsa and Szemerédi14
] in which they proved the first version of the graph removal lemma, they also proved that when F is the triangle
$\mbox{poly}(\varepsilon)n^{v(F)}$
copies of F. In the seminal paper of Ruzsa and Szemerédi [
Reference Ruzsa and Szemerédi14
] in which they proved the first version of the graph removal lemma, they also proved that when F is the triangle
![]() $K_3$
, the removal lemma has a super-polynomial dependence on
$K_3$
, the removal lemma has a super-polynomial dependence on
![]() $\varepsilon$
. A highly influential result of Alon [
Reference Alon1
] completed the picture by extending the result of [
Reference Ruzsa and Szemerédi14
] to all non-bipartite graphs F.
$\varepsilon$
. A highly influential result of Alon [
Reference Alon1
] completed the picture by extending the result of [
Reference Ruzsa and Szemerédi14
] to all non-bipartite graphs F.
Moving now to general
![]() $k \gt 2$
, it is natural to ask for which k-graphs the function
$k \gt 2$
, it is natural to ask for which k-graphs the function
![]() $\delta(F,\varepsilon)$
depends polynomially on
$\delta(F,\varepsilon)$
depends polynomially on
![]() $\varepsilon$
. Let us say that in this case the F-removal lemma is polynomial. It is easy to see that like in the case of graphs, the F-removal lemma is polynomial whenever F is k-partite. This follows from Erdős’s [
Reference Erdős4
] well-known hypergraph extension of the Kővári–Sós–Turán theorem. Motivated by Alon’s result [
Reference Alon1
] mentioned above, Kohayakawa, Nagle and Rödl [
Reference Kohayakawa, Nagle and Rödl9
] conjectured in 2002 that the F-removal lemma is polynomial if and only if F is k-partite. They further proved that the F-removal lemma is not polynomial when F is the complete k-graph on
$\varepsilon$
. Let us say that in this case the F-removal lemma is polynomial. It is easy to see that like in the case of graphs, the F-removal lemma is polynomial whenever F is k-partite. This follows from Erdős’s [
Reference Erdős4
] well-known hypergraph extension of the Kővári–Sós–Turán theorem. Motivated by Alon’s result [
Reference Alon1
] mentioned above, Kohayakawa, Nagle and Rödl [
Reference Kohayakawa, Nagle and Rödl9
] conjectured in 2002 that the F-removal lemma is polynomial if and only if F is k-partite. They further proved that the F-removal lemma is not polynomial when F is the complete k-graph on
![]() $k+1$
vertices. Alon and the second author [
Reference Alon and Shapira2
] proved that a more general condition guarantees that the F-removal lemma is not polynomial, but fell short of covering all non-k-partite k-graphs. In this paper we complete the picture, by fully resolving the problem of Kohayakawa, Nagle and Rödl [
Reference Kohayakawa, Nagle and Rödl9
].
$k+1$
vertices. Alon and the second author [
Reference Alon and Shapira2
] proved that a more general condition guarantees that the F-removal lemma is not polynomial, but fell short of covering all non-k-partite k-graphs. In this paper we complete the picture, by fully resolving the problem of Kohayakawa, Nagle and Rödl [
Reference Kohayakawa, Nagle and Rödl9
].
Theorem 1. For every k-graph F, the F-removal lemma is polynomial if and only if F is k-partite.
As a related remark, we note that for
![]() $k \geq 3$
, the analogous problem for the induced F-removal lemma (that is, a characterisation of k-graphs for which the induced F-removal lemma has polynomial bounds) was recently settled in [
Reference Gishboliner and Tomon6
], following a nearly-complete characterisation given in [
Reference Alon and Shapira2
].
$k \geq 3$
, the analogous problem for the induced F-removal lemma (that is, a characterisation of k-graphs for which the induced F-removal lemma has polynomial bounds) was recently settled in [
Reference Gishboliner and Tomon6
], following a nearly-complete characterisation given in [
Reference Alon and Shapira2
].
Before proceeding, let us recall the notion of a core, which plays an important role in the proof of Theorem 1. Recall that for a pair of k-graphs
![]() $F_1,F_2$
, a homomorphism from
$F_1,F_2$
, a homomorphism from
![]() $F_1$
to
$F_1$
to
![]() $F_2$
is a map
$F_2$
is a map
![]() $\varphi\,:\,V(F_1) \rightarrow V(F_2)$
such that for every
$\varphi\,:\,V(F_1) \rightarrow V(F_2)$
such that for every
![]() $e \in E(F_1)$
it holds that
$e \in E(F_1)$
it holds that
![]() $\{\varphi(x)\,:\,x\in e\} \in E(F_2)$
. The core of a k-graph F is the smallest (with respect to the number of vertices) subgraph of F to which there is a homomorphism from F. It is not hard to show that the core of F is unique up to isomorphismFootnote 2. Also, note that the core of a k-graph F is a single edge if and only if F is k-partite. In particular, if a k-graph is not k-partite, then neither is its core. We say that F is a core if it is the core of itself.
$\{\varphi(x)\,:\,x\in e\} \in E(F_2)$
. The core of a k-graph F is the smallest (with respect to the number of vertices) subgraph of F to which there is a homomorphism from F. It is not hard to show that the core of F is unique up to isomorphismFootnote 2. Also, note that the core of a k-graph F is a single edge if and only if F is k-partite. In particular, if a k-graph is not k-partite, then neither is its core. We say that F is a core if it is the core of itself.
Alon’s [
Reference Alon1
] approach relies on the fact that the core of every non-bipartite graph has a cycle. It is then natural to try and prove Theorem 1 by finding analogous sub-structures in the core of every non-k-partite k-graphs. Indeed, this was the approach taken in [
Reference Alon and Shapira2, Reference Kohayakawa, Nagle and Rödl9
]. The main novelty in this paper, and what allows us to handle all cases of Theorem 1, is that instead of directly inspecting the k-graph F, we study the properties of a certain graph associated with F. More precisely, given a k-graph
![]() $F=(V,E)$
, we consider its 2-shadow, which is the graph on the same vertex set V in which
$F=(V,E)$
, we consider its 2-shadow, which is the graph on the same vertex set V in which
![]() $\{u,v\}$
is an edge if and only if u,v belong to some
$\{u,v\}$
is an edge if and only if u,v belong to some
![]() $e \in E$
. The proof of Theorem 1 relies on the two lemmas described below.
$e \in E$
. The proof of Theorem 1 relies on the two lemmas described below.
Lemma 1·1. Suppose a k-graph F is a core and its 2-shadow contains an induced cycle of length at least 4. Then the F-removal lemma is not polynomial. Footnote 3
Note that this is a generalisation of Alon’s result mentioned above since the 2-shadow of every non-bipartite graph F (which is of course F itself in this case) must contain a cycle. Our second lemma is the following.
Lemma 1·2.
Suppose a k-graph F is a core and its 2-shadow contains a clique of size
![]() $k+1$
. Then the F-removal lemma is not polynomial.
$k+1$
. Then the F-removal lemma is not polynomial.
Note that this is a generalisation of the result of Kohayakawa, Nagle and Rödl [
Reference Kohayakawa, Nagle and Rödl9
] mentioned above since the 2-shadow of the complete k-graph on
![]() $k+1$
vertices is a clique of size
$k+1$
vertices is a clique of size
![]() $k+1$
.
$k+1$
.
The proofs of Lemmas 1·1 and 1·2 appear in Section 2, but let us first see why they together allow us to handle all non-k-partite k-graphs, thus proving Theorem 1.
Proof of Theorem
1. The “if” part was discussed above. As for the “only if” part, suppose F is a k-graph which is not k-partite and assume first that F is a core. Let G denote the 2-shadow of F. If G contains an induced cycle of length at least 4, then the result follows from Lemma 1·1. Suppose then that G contains no such cycle, implying that G is chordal. Since F is not k-partite, G is not k-colourable. Since G is assumed to be chordal, and chordal graphs are well-known to be perfect, this means that G has a clique of size
![]() $k+1$
. Hence, the result follows from Lemma 1·2.
$k+1$
. Hence, the result follows from Lemma 1·2.
To prove the result when F is not necessarily a core, one just needs to observe that if
![]() $F'$
is the core of F, then (i) as noted earlier,
$F'$
is the core of F, then (i) as noted earlier,
![]() $F'$
is not k-partite, and (ii) since the
$F'$
is not k-partite, and (ii) since the
![]() $F'$
removal lemma is not polynomial (by the previous paragraph), then neither is the F-removal lemma (see Claim 2·1 for the short proof of this fact).
$F'$
removal lemma is not polynomial (by the previous paragraph), then neither is the F-removal lemma (see Claim 2·1 for the short proof of this fact).
2. Proofs of Lemmas 1.1 and 1.2
We start by introducing some recurring notions. Recall that the b-blowup of a k-graph
![]() $H=(V,E)$
is the k-graph obtained by replacing every vertex
$H=(V,E)$
is the k-graph obtained by replacing every vertex
![]() $v\in V$
with a b-tuple of vertices
$v\in V$
with a b-tuple of vertices
![]() $S_v$
, and then replacing every edge
$S_v$
, and then replacing every edge
![]() $e=\{v_1,\ldots,v_k\} \in E$
with all possible
$e=\{v_1,\ldots,v_k\} \in E$
with all possible
![]() $b^k$
edges
$b^k$
edges
![]() $S_{v_1} \times S_{v_2} \times \cdots \times S_{v_k}$
. Note that if
$S_{v_1} \times S_{v_2} \times \cdots \times S_{v_k}$
. Note that if
![]() $H'$
is the b-blowup of H, then the map sending
$H'$
is the b-blowup of H, then the map sending
![]() $S_v$
to v is a homomorphism from
$S_v$
to v is a homomorphism from
![]() $H'$
to H. We will frequently refer to this as the natural homomorphism from
$H'$
to H. We will frequently refer to this as the natural homomorphism from
![]() $H'$
to H. We say that a k-graph H is homomorphic to a k-graph F if there is a homomorphism from H to F. We first prove the following assertion, which was used in the proof of Theorem 1.
$H'$
to H. We say that a k-graph H is homomorphic to a k-graph F if there is a homomorphism from H to F. We first prove the following assertion, which was used in the proof of Theorem 1.
Claim 2·1. Let F be a k-graph and let C be a subgraph of F so that F is homomorphic to C. Then, if the C-removal lemma is not polynomial, then neither is the F-removal lemma.
Proof. Since the C-removal lemma is not polynomial, there is a function
![]() $\delta\,:\,(0,1) \rightarrow (0,1)$
such that
$\delta\,:\,(0,1) \rightarrow (0,1)$
such that
![]() $1/\delta(\varepsilon)$
grows faster than any polynomial in
$1/\delta(\varepsilon)$
grows faster than any polynomial in
![]() $1/\varepsilon$
, and such that for every
$1/\varepsilon$
, and such that for every
![]() $\varepsilon \gt 0$
and large enough n there is an n-vertex k-graph
$\varepsilon \gt 0$
and large enough n there is an n-vertex k-graph
![]() $H_1$
which contains a collection
$H_1$
which contains a collection
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $\varepsilon n^k$
edge-disjoint copies of C but only
$\varepsilon n^k$
edge-disjoint copies of C but only
![]() $\delta n^{v(C)}$
copies of C altogether. Let H be the v(F)-blowup of
$\delta n^{v(C)}$
copies of C altogether. Let H be the v(F)-blowup of
![]() $H_1$
. Note that the v(F)-blowup of C contains a copy of F. Also, copies of F corresponding to different copies of C from
$H_1$
. Note that the v(F)-blowup of C contains a copy of F. Also, copies of F corresponding to different copies of C from
![]() $\mathcal{C}$
are edge-disjoint. Hence, H has a collection of
$\mathcal{C}$
are edge-disjoint. Hence, H has a collection of
![]() $\varepsilon n^k = \varepsilon (v(H)/v(F))^k = \Omega(\varepsilon \cdot v(H)^k) = \varepsilon' v(H)^k$
edge-disjoint copies of F, for a suitable
$\varepsilon n^k = \varepsilon (v(H)/v(F))^k = \Omega(\varepsilon \cdot v(H)^k) = \varepsilon' v(H)^k$
edge-disjoint copies of F, for a suitable
![]() $\varepsilon' = \Omega(\varepsilon)$
. Let us bound the total number of copies of F in H. Since C is a subgraph of F, each copy of F must contain a copy of C. Let
$\varepsilon' = \Omega(\varepsilon)$
. Let us bound the total number of copies of F in H. Since C is a subgraph of F, each copy of F must contain a copy of C. Let
![]() $\varphi\,:\,V(H) \rightarrow V(H_1)$
be the natural homomorphism from H to
$\varphi\,:\,V(H) \rightarrow V(H_1)$
be the natural homomorphism from H to
![]() $H_1$
(as defined above). For each copy
$H_1$
(as defined above). For each copy
![]() $C'$
of C in H, consider the subgraph
$C'$
of C in H, consider the subgraph
![]() $\varphi(C')$
of
$\varphi(C')$
of
![]() $H_1$
. The number of copies
$H_1$
. The number of copies
![]() $C'$
of C with
$C'$
of C with
![]() $v(\varphi(C')) \lt v(C)$
is at most
$v(\varphi(C')) \lt v(C)$
is at most
![]() $v(F)^{v(C)} \cdot O(n^{v(C) - 1}) \leq \delta n^{v(C)}$
, provided that n is large enough. The number of copies
$v(F)^{v(C)} \cdot O(n^{v(C) - 1}) \leq \delta n^{v(C)}$
, provided that n is large enough. The number of copies
![]() $C'$
of C with
$C'$
of C with
![]() $\varphi(C') \cong C$
is at most
$\varphi(C') \cong C$
is at most
![]() $v(F)^{v(C)} \cdot \delta n^{v(C)} = O(\delta n^{v(C)})$
, because
$v(F)^{v(C)} \cdot \delta n^{v(C)} = O(\delta n^{v(C)})$
, because
![]() $H_1$
contains at most
$H_1$
contains at most
![]() $\delta n^{v(C)}$
copies of C. So in total, H contains at most
$\delta n^{v(C)}$
copies of C. So in total, H contains at most
![]() $O(\delta n^{v(C)})$
copies of C. This means that H contains at most
$O(\delta n^{v(C)})$
copies of C. This means that H contains at most
![]() $O(\delta n^{v(C)}) \cdot v(H)^{v(F) - v(C)} = {}O(\delta \cdot v(H)^{v(F)}) = \delta' v(H)^{v(F)}$
copies of F, for a suitable
$O(\delta n^{v(C)}) \cdot v(H)^{v(F) - v(C)} = {}O(\delta \cdot v(H)^{v(F)}) = \delta' v(H)^{v(F)}$
copies of F, for a suitable
![]() $\delta' = O(\delta)$
. Note that
$\delta' = O(\delta)$
. Note that
![]() $1/\delta'$
is super-polynomial in
$1/\delta'$
is super-polynomial in
![]() $1/\varepsilon'$
. This shows that the F-removal lemma is not polynomial.
$1/\varepsilon'$
. This shows that the F-removal lemma is not polynomial.
Since the core of F satisfies the properties of C in the above claim, it indeed establishes the assertion which we used when proving Theorem 1, namely that it suffices to prove the theorem when F is a core.
It thus remains to prove Lemmas 1·1 and 1·2. We begin preparing these proofs with some auxiliary lemmas. The following is a key property of cores that we will use in this section.
Claim 2·2.
Let F be a core k-graph, let H be a k-graph, and let
![]() $\varphi\,:\,H \rightarrow F$
be a homomorphism. Then for every copy
$\varphi\,:\,H \rightarrow F$
be a homomorphism. Then for every copy
![]() $F'$
of F in H, the map
$F'$
of F in H, the map
![]() $\varphi_{|{V(F')}}$
is an isomorphism.
$\varphi_{|{V(F')}}$
is an isomorphism.
Proof. We first observe that every homomorphism from a core F to itself is an isomorphism. Indeed, by definition, F is the core of itself, meaning that there is no homomorphism from F to a subgraph
![]() $F_0$
of F with
$F_0$
of F with
![]() $V(F_0) \subsetneq V(F)$
. Hence, every homomorphism from F to itself is a bijection, and hence an isomorphism. The assertion of the claim now follows from the fact that
$V(F_0) \subsetneq V(F)$
. Hence, every homomorphism from F to itself is a bijection, and hence an isomorphism. The assertion of the claim now follows from the fact that
![]() $\varphi_{|{V(F')}}$
is a homomorphism from
$\varphi_{|{V(F')}}$
is a homomorphism from
![]() $F'$
(which is a copy of F) to F.
$F'$
(which is a copy of F) to F.
The following definition will play an important role in our proofs. Let F be a k-graph on vertex-set [f] and let G be an f-partite k-graph with sides
![]() $V_1,\ldots,V_f$
. A canonical copy of F in G is a copy consisting of vertices
$V_1,\ldots,V_f$
. A canonical copy of F in G is a copy consisting of vertices
![]() $v_1 \in V_1,\ldots,v_f \in V_f$
in which
$v_1 \in V_1,\ldots,v_f \in V_f$
in which
![]() $v_i$
plays the role of
$v_i$
plays the role of
![]() $i \in V(F)$
for each
$i \in V(F)$
for each
![]() $i = 1,\ldots,f$
. Note that if G is homomorphic to F via the homomorphism mapping
$i = 1,\ldots,f$
. Note that if G is homomorphic to F via the homomorphism mapping
![]() $V_i$
to i (for each
$V_i$
to i (for each
![]() $i=1,\ldots,f$
), and if furthermore F is a core, then every copy of F in G is canonical; this follows from Claim 2·2.
$i=1,\ldots,f$
), and if furthermore F is a core, then every copy of F in G is canonical; this follows from Claim 2·2.
We now describe our approach for proving Lemma 1·1 (the approach for Lemma 1·2 is similar). Let
![]() $I \subseteq V(F)$
be a set of vertices so that the 2-shadow of F induced on I is a cycle
$I \subseteq V(F)$
be a set of vertices so that the 2-shadow of F induced on I is a cycle
![]() $C_t$
,
$C_t$
,
![]() $t \geq 4$
. Then
$t \geq 4$
. Then
![]() $|I \cap e| \leq 2$
for every
$|I \cap e| \leq 2$
for every
![]() $e \in E(F)$
. We first use a construction from [
Reference Alon1
], giving a t-partite graph which consists of many edge-disjoint canonical copies of
$e \in E(F)$
. We first use a construction from [
Reference Alon1
], giving a t-partite graph which consists of many edge-disjoint canonical copies of
![]() $C_t$
, yet contains only few canonical copies of
$C_t$
, yet contains only few canonical copies of
![]() $C_t$
altogether. The second step is then to extend the graph thus constructed into a k-graph containing many edge-disjoint copies of F yet few copies of F. The following lemma will help us in performing this extension. For
$C_t$
altogether. The second step is then to extend the graph thus constructed into a k-graph containing many edge-disjoint copies of F yet few copies of F. The following lemma will help us in performing this extension. For
![]() $\ell \geq 1$
, two sets are called
$\ell \geq 1$
, two sets are called
![]() $\ell$
-disjoint if their intersection has size at most
$\ell$
-disjoint if their intersection has size at most
![]() $\ell-1$
. Two subgraphs of a hypergraph are called
$\ell-1$
. Two subgraphs of a hypergraph are called
![]() $\ell$
-disjoint if their vertex-sets are
$\ell$
-disjoint if their vertex-sets are
![]() $\ell$
-disjoint. In what follows, when considering an s-partite hypergraph with parts
$\ell$
-disjoint. In what follows, when considering an s-partite hypergraph with parts
![]() $V_1,\ldots,V_s$
, we will refer to the edges as sets or s-tuples, interchangeably. Moreover, we will use both set notation and s-tuple notation. For example, for
$V_1,\ldots,V_s$
, we will refer to the edges as sets or s-tuples, interchangeably. Moreover, we will use both set notation and s-tuple notation. For example, for
![]() $F \in V_1 \times \ldots \times V_s$
, we write F(i) for the i’th coordinate of F; and for
$F \in V_1 \times \ldots \times V_s$
, we write F(i) for the i’th coordinate of F; and for
![]() $F_1,F_2 \in V_1 \times \ldots \times V_s$
, we write
$F_1,F_2 \in V_1 \times \ldots \times V_s$
, we write
![]() $F_1 \cap F_2$
for the intersection of
$F_1 \cap F_2$
for the intersection of
![]() $F_1,F_2$
as sets.
$F_1,F_2$
as sets.
Lemma 2·3.
Let
![]() $r,s,k,\ell \geq 0$
satisfy
$r,s,k,\ell \geq 0$
satisfy
![]() $k \geq \ell$
and
$k \geq \ell$
and
![]() $r \geq k-\ell$
. Let
$r \geq k-\ell$
. Let
![]() $V_1,\ldots,V_s,V_{s+1},\ldots,V_{s+r}$
be pairwise-disjoint sets of size n each. Let
$V_1,\ldots,V_s,V_{s+1},\ldots,V_{s+r}$
be pairwise-disjoint sets of size n each. Let
![]() $\mathcal{S} \subseteq V_1 \times \ldots \times V_s$
be a family of
$\mathcal{S} \subseteq V_1 \times \ldots \times V_s$
be a family of
![]() $\ell$
-disjoint sets. Then there is a family
$\ell$
-disjoint sets. Then there is a family
![]() $\mathcal{F} \subseteq V_1 \times \ldots \times V_{s+r}$
with the following properties:
$\mathcal{F} \subseteq V_1 \times \ldots \times V_{s+r}$
with the following properties:
-
(i) for every
 $F \in \mathcal{F}$
it holds that
$F \in \mathcal{F}$
it holds that
 $F|_{V_1 \times \ldots \times V_s} \in \mathcal{S}$
;
$F|_{V_1 \times \ldots \times V_s} \in \mathcal{S}$
; -
(ii)
 $|\mathcal{F}| = \Omega_{r,s,k}(|\mathcal{S}| n^{k-\ell})$
;
$|\mathcal{F}| = \Omega_{r,s,k}(|\mathcal{S}| n^{k-\ell})$
; -
(iii) for every pair of distinct
 $F_1,F_2 \in \mathcal{F}$
, if
$F_1,F_2 \in \mathcal{F}$
, if
 $|F_1 \cap F_2| \geq k$
then
$|F_1 \cap F_2| \geq k$
then  $$ \#\{s+1 \leq i \leq s+r\,:\,F_1(i) = F_2(i)\} \leq k-\ell-1.$$
$$ \#\{s+1 \leq i \leq s+r\,:\,F_1(i) = F_2(i)\} \leq k-\ell-1.$$
Proof. We construct the family
![]() $\mathcal{F}$
as follows. For each
$\mathcal{F}$
as follows. For each
![]() $S \in \mathcal{S}$
and each r-tuple
$S \in \mathcal{S}$
and each r-tuple
![]() $A \in V_{s+1} \times \ldots \times V_{s+r}$
, add
$A \in V_{s+1} \times \ldots \times V_{s+r}$
, add
![]() $S \cup A$
to
$S \cup A$
to
![]() $\mathcal{F}$
with probability
$\mathcal{F}$
with probability
![]() $1/(Cn^{r-k+\ell})$
and independently, where C is a large constant to be chosen later. (i) is satisfied by definition. Let us estimate the number of pairs
$1/(Cn^{r-k+\ell})$
and independently, where C is a large constant to be chosen later. (i) is satisfied by definition. Let us estimate the number of pairs
![]() $F_1,F_2 \in \mathcal{F}$
violating (iii); denote this number by B. We claim that
$F_1,F_2 \in \mathcal{F}$
violating (iii); denote this number by B. We claim that
To this end, suppose that
![]() $F_1,F_2 \in \mathcal{F}$
violate (iii), and write
$F_1,F_2 \in \mathcal{F}$
violate (iii), and write
![]() $F_1 = S_1 \cup A_1$
and
$F_1 = S_1 \cup A_1$
and
![]() $F_2 = S_2 \cup A_2$
, where
$F_2 = S_2 \cup A_2$
, where
![]() $S_1,S_2 \in \mathcal{F}$
and
$S_1,S_2 \in \mathcal{F}$
and
![]() $A_1,A_2 \in V_{s+1} \times \ldots \times V_{s+r}$
. Suppose first that
$A_1,A_2 \in V_{s+1} \times \ldots \times V_{s+r}$
. Suppose first that
![]() $S_1 = S_2$
. Then there are
$S_1 = S_2$
. Then there are
![]() $|\mathcal{S}|$
choices for
$|\mathcal{S}|$
choices for
![]() $S_1,S_2$
. Also, to violate (iii), it must hold that
$S_1,S_2$
. Also, to violate (iii), it must hold that
![]() $|A_1 \cap A_2| \geq k-\ell$
. The number of choices of
$|A_1 \cap A_2| \geq k-\ell$
. The number of choices of
![]() $A_1,A_2 \in V_{s+1} \times \ldots \times V_{s+r}$
with
$A_1,A_2 \in V_{s+1} \times \ldots \times V_{s+r}$
with
![]() $|A_1 \cap A_2| \geq k-\ell$
is at most
$|A_1 \cap A_2| \geq k-\ell$
is at most
![]() $n^{r} \cdot \binom{r}{k-\ell} \cdot n^{r-k+\ell}$
. Finally, the probability that
$n^{r} \cdot \binom{r}{k-\ell} \cdot n^{r-k+\ell}$
. Finally, the probability that
![]() $F_1,F_2 \in \mathcal{F}$
is
$F_1,F_2 \in \mathcal{F}$
is
![]() $1/(Cn^{r-k+\ell})^2$
. Hence, the expected number of violations of this type (i.e., with
$1/(Cn^{r-k+\ell})^2$
. Hence, the expected number of violations of this type (i.e., with
![]() $S_1 = S_2$
) is at most
$S_1 = S_2$
) is at most
![]() $|\mathcal{S}| \cdot n^{r} \cdot \binom{r}{k-\ell} \cdot n^{r-k+\ell} \cdot 1/(Cn^{r-k+\ell})^2 = O_{s,r,k}\left({1}/{C^2} \right) \cdot |\mathcal{S}| \cdot n^{k-\ell}$
.
$|\mathcal{S}| \cdot n^{r} \cdot \binom{r}{k-\ell} \cdot n^{r-k+\ell} \cdot 1/(Cn^{r-k+\ell})^2 = O_{s,r,k}\left({1}/{C^2} \right) \cdot |\mathcal{S}| \cdot n^{k-\ell}$
.
Now consider the case that
![]() $S_1 \neq S_2$
, and put
$S_1 \neq S_2$
, and put
![]() $t := |S_1 \cap S_2|$
. As the sets in
$t := |S_1 \cap S_2|$
. As the sets in
![]() $\mathcal{S}$
are pairwise
$\mathcal{S}$
are pairwise
![]() $\ell$
-disjoint, we have
$\ell$
-disjoint, we have
![]() $t \leq \ell-1$
. Also, the number of choices for
$t \leq \ell-1$
. Also, the number of choices for
![]() $S_1,S_2 \in \mathcal{S}$
with
$S_1,S_2 \in \mathcal{S}$
with
![]() $|S_1 \cap S_2| = t$
is at most
$|S_1 \cap S_2| = t$
is at most
![]() $|\mathcal{S}| \cdot \binom{s}{t} \cdot n^{\ell-t}$
, again using that the sets in
$|\mathcal{S}| \cdot \binom{s}{t} \cdot n^{\ell-t}$
, again using that the sets in
![]() $\mathcal{S}$
are pairwise
$\mathcal{S}$
are pairwise
![]() $\ell$
-disjoint. In order for
$\ell$
-disjoint. In order for
![]() $F_1,F_2$
to violate (iii), we must have
$F_1,F_2$
to violate (iii), we must have
![]() $|A_1 \cap A_2| \geq k-t$
. The number of choices for
$|A_1 \cap A_2| \geq k-t$
. The number of choices for
![]() $A_1,A_2 \in V_{s+1} \times \ldots \times V_{s+r}$
with
$A_1,A_2 \in V_{s+1} \times \ldots \times V_{s+r}$
with
![]() $|A_1 \cap A_2| \geq k-t$
is at most
$|A_1 \cap A_2| \geq k-t$
is at most
![]() $n^{r} \cdot \binom{r}{k-t} \cdot n^{r-k+t}$
. Finally, as before, the probability that
$n^{r} \cdot \binom{r}{k-t} \cdot n^{r-k+t}$
. Finally, as before, the probability that
![]() $F_1,F_2 \in \mathcal{F}$
is
$F_1,F_2 \in \mathcal{F}$
is
![]() $1/(Cn^{r-k+\ell})^2$
. Hence, the expected number of violations of this type (i.e., with
$1/(Cn^{r-k+\ell})^2$
. Hence, the expected number of violations of this type (i.e., with
![]() $S_1 \neq S_2$
) is at most
$S_1 \neq S_2$
) is at most
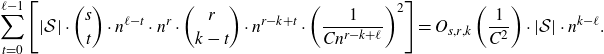 $$ {}\sum_{t=0}^{\ell-1} \left[ |\mathcal{S}| \cdot \binom{s}{t} \cdot n^{\ell-t} \cdot n^{r} \cdot \binom{r}{k-t} \cdot n^{r-k+t} \cdot \left(\frac{1}{Cn^{r-k+\ell}}\right)^2 \right] = {}O_{s,r,k}\left(\frac{1}{C^2} \right) \cdot |\mathcal{S}| \cdot n^{k-\ell}. $$
$$ {}\sum_{t=0}^{\ell-1} \left[ |\mathcal{S}| \cdot \binom{s}{t} \cdot n^{\ell-t} \cdot n^{r} \cdot \binom{r}{k-t} \cdot n^{r-k+t} \cdot \left(\frac{1}{Cn^{r-k+\ell}}\right)^2 \right] = {}O_{s,r,k}\left(\frac{1}{C^2} \right) \cdot |\mathcal{S}| \cdot n^{k-\ell}. $$
This proves (2
![]() $ \cdot $
1). Now note that the expected size of
$ \cdot $
1). Now note that the expected size of
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $|\mathcal{S}| \cdot n^r \cdot {1}/{Cn^{r-k+\ell}} = {1}/{C} \cdot |\mathcal{S}| \cdot n^{k-\ell}$
. So by choosing C to be large enough (as a function of s,r,k), we can guarantee that
$|\mathcal{S}| \cdot n^r \cdot {1}/{Cn^{r-k+\ell}} = {1}/{C} \cdot |\mathcal{S}| \cdot n^{k-\ell}$
. So by choosing C to be large enough (as a function of s,r,k), we can guarantee that
![]() $\mathbb{E}[|\mathcal{F}| - B] \geq {1}/{2C} \cdot |\mathcal{S}| \cdot n^{k-\ell}$
. By fixing such a choice of
$\mathbb{E}[|\mathcal{F}| - B] \geq {1}/{2C} \cdot |\mathcal{S}| \cdot n^{k-\ell}$
. By fixing such a choice of
![]() $\mathcal{F}$
and deleting one set
$\mathcal{F}$
and deleting one set
![]() $F \in \mathcal{F}$
from each violation, we get the required conclusion.
$F \in \mathcal{F}$
from each violation, we get the required conclusion.
The following well-known fact is an easy corollary of Lemma 2·3.
Lemma 2·4.
Let
![]() $1 \leq k \leq r$
, and let
$1 \leq k \leq r$
, and let
![]() $V_1,\ldots,V_r$
be pairwise-disjoint sets of size n each. Then there is
$V_1,\ldots,V_r$
be pairwise-disjoint sets of size n each. Then there is
![]() $\mathcal{F} \subseteq V_1 \times \ldots \times V_r$
,
$\mathcal{F} \subseteq V_1 \times \ldots \times V_r$
,
![]() $|\mathcal{F}| \geq \Omega(n^{k})$
, such that the r-sets in
$|\mathcal{F}| \geq \Omega(n^{k})$
, such that the r-sets in
![]() $\mathcal{F}$
are k-disjoint.
$\mathcal{F}$
are k-disjoint.
Proof. Apply Lemma 2·3 with
![]() $s = \ell = 0$
and
$s = \ell = 0$
and
![]() $\mathcal{S} = \{\emptyset\}$
.
$\mathcal{S} = \{\emptyset\}$
.
The next lemma shows why constructing a k-graph with many edge-disjoint copies of F but at most
![]() $n^{v(F)-1}$
copies of F in total can be boosted to prove Lemmas 1·1 and 1·2. The lemma makes crucial use of the fact that F is a core.
$n^{v(F)-1}$
copies of F in total can be boosted to prove Lemmas 1·1 and 1·2. The lemma makes crucial use of the fact that F is a core.
Lemma 2·5.
Let F be a core k-graph, and suppose that for every
![]() $\delta \gt 0$
and large enough n, there is an n-vertex k-graph H which is homomorphic to F, has a collection of at least
$\delta \gt 0$
and large enough n, there is an n-vertex k-graph H which is homomorphic to F, has a collection of at least
![]() $n^{k-\delta}$
edge-disjoint copies of F, but has at most
$n^{k-\delta}$
edge-disjoint copies of F, but has at most
![]() $n^{v(F) - 1}$
copies of F altogether. Then the F-removal lemma is not polynomial.
$n^{v(F) - 1}$
copies of F altogether. Then the F-removal lemma is not polynomial.
Proof. Let
![]() $\varepsilon \gt 0$
and let n be large enough. Let m be the largest integer satisfying
$\varepsilon \gt 0$
and let n be large enough. Let m be the largest integer satisfying
![]() $m^{\delta} \leq 1/\varepsilon$
, so that
$m^{\delta} \leq 1/\varepsilon$
, so that
![]() $m \geq (1/\varepsilon)^{1/(2\delta)}$
, say. Let H be the k-graph guaranteed to exist by the assumption of the lemma, but with m in place of n. So H has m vertices, is homomorphic to F, contains a collection
$m \geq (1/\varepsilon)^{1/(2\delta)}$
, say. Let H be the k-graph guaranteed to exist by the assumption of the lemma, but with m in place of n. So H has m vertices, is homomorphic to F, contains a collection
![]() $\mathcal{F}$
of
$\mathcal{F}$
of
![]() $m^{k-\delta} \geq \varepsilon m^k$
edge-disjoint copies of F, but has at most
$m^{k-\delta} \geq \varepsilon m^k$
edge-disjoint copies of F, but has at most
![]() $m^{v(F) - 1}$
copies of F altogether.
$m^{v(F) - 1}$
copies of F altogether.
Let G be the
![]() ${n}/{m}$
-blowup of H. Each
${n}/{m}$
-blowup of H. Each
![]() $F' \in \mathcal{F}$
gives rise to
$F' \in \mathcal{F}$
gives rise to
![]() $\Omega(({n}/{m})^k)$
k-disjoint (and hence also edge-disjoint) copies of F in G, by Lemma 2·4 applied with
$\Omega(({n}/{m})^k)$
k-disjoint (and hence also edge-disjoint) copies of F in G, by Lemma 2·4 applied with
![]() $r = v(F)$
and with
$r = v(F)$
and with
![]() ${n}/{m}$
in place of n. Copies arising from different
${n}/{m}$
in place of n. Copies arising from different
![]() $F'_1,F'_2 \in \mathcal{F}$
are edge-disjoint, because the copies in
$F'_1,F'_2 \in \mathcal{F}$
are edge-disjoint, because the copies in
![]() $\mathcal{F}$
are edge-disjoint. Altogether, this gives a collection of
$\mathcal{F}$
are edge-disjoint. Altogether, this gives a collection of
![]() $\varepsilon m^k \cdot \Omega(({n}/{m})^k) = \Omega(\varepsilon n^k)$
edge-disjoint copies of F in G.
$\varepsilon m^k \cdot \Omega(({n}/{m})^k) = \Omega(\varepsilon n^k)$
edge-disjoint copies of F in G.
Let us upper-bound the total number of copies of F in G. By assumption, there is a homomorphism
![]() $\varphi$
from H to F. Let
$\varphi$
from H to F. Let
![]() $\psi$
be the “natural” homomorphism from G to H (as described in the beginning of this section). Then
$\psi$
be the “natural” homomorphism from G to H (as described in the beginning of this section). Then
![]() $\varphi \circ \psi$
is a homomorphism from G to F. By Claim 2·2, for every copy
$\varphi \circ \psi$
is a homomorphism from G to F. By Claim 2·2, for every copy
![]() $F'$
of F in G the map
$F'$
of F in G the map
![]() $(\varphi \circ \psi)|_{{V(F')}}$
is an isomorphism from
$(\varphi \circ \psi)|_{{V(F')}}$
is an isomorphism from
![]() $F'$
to F. We claim that this means that
$F'$
to F. We claim that this means that
![]() $\psi$
maps every copy
$\psi$
maps every copy
![]() $F'$
of F in G onto a copy of F in H. Indeed,
$F'$
of F in G onto a copy of F in H. Indeed,
![]() $\psi|_{{V(F')}}$
must be injective (otherwise
$\psi|_{{V(F')}}$
must be injective (otherwise
![]() $(\varphi \circ \psi)|_{{V(F')}}$
would not be an isomorphism), and since
$(\varphi \circ \psi)|_{{V(F')}}$
would not be an isomorphism), and since
![]() $\psi|_{{V(F')}}$
must map edges to edges (on account of being a homomorphism) its image must contain a copy of F. We thus see that every copy of F in G must come from the blown-up copies of F in H. But each copy of F in H gives rise to
$\psi|_{{V(F')}}$
must map edges to edges (on account of being a homomorphism) its image must contain a copy of F. We thus see that every copy of F in G must come from the blown-up copies of F in H. But each copy of F in H gives rise to
![]() $({n}/{m})^{v(F)}$
copies of F in G. Hence, the total number of copies of F in G is at most
$({n}/{m})^{v(F)}$
copies of F in G. Hence, the total number of copies of F in G is at most
Since
![]() $\delta \gt 0$
is arbitrary, this shows that the F-removal lemma is not polynomial.
$\delta \gt 0$
is arbitrary, this shows that the F-removal lemma is not polynomial.
The following result is implicit in [ Reference Alon1 ]. For the sake of completeness, we include a proof.
Lemma 2·6.
Let
![]() $t \geq 3$
. Then for every large enough n, there is a t-partite graph G with sides
$t \geq 3$
. Then for every large enough n, there is a t-partite graph G with sides
![]() $V_1,\ldots,V_{t}$
, each of size n, such that G has a collection of
$V_1,\ldots,V_{t}$
, each of size n, such that G has a collection of
![]() $n^2/e^{O(\sqrt{\log n})} = n^{2-o(1)}$
2-disjoint canonical copies of
$n^2/e^{O(\sqrt{\log n})} = n^{2-o(1)}$
2-disjoint canonical copies of
![]() $C_t$
, but at most
$C_t$
, but at most
![]() $n^{t-1}$
canonical copies of
$n^{t-1}$
canonical copies of
![]() $C_t$
altogether.
$C_t$
altogether.
Proof. Suppose that the vertices of
![]() $C_{t}$
are
$C_{t}$
are
![]() $1,2,\ldots,t$
(appearing in this order along the cycle). Take a set
$1,2,\ldots,t$
(appearing in this order along the cycle). Take a set
![]() $B \subseteq [n/t]$
,
$B \subseteq [n/t]$
,
![]() $|B| \geq n/e^{O\sqrt{\log n}}$
, with no non-trivial solution to the linear equation
$|B| \geq n/e^{O\sqrt{\log n}}$
, with no non-trivial solution to the linear equation
![]() $y_1 + \ldots + y_{t-1} = (t-1)y_{t}$
with
$y_1 + \ldots + y_{t-1} = (t-1)y_{t}$
with
![]() $y_1,\ldots,y_{t} \in B$
(where a solution is trivial if
$y_1,\ldots,y_{t} \in B$
(where a solution is trivial if
![]() $y_1=y_2=\cdots=y_{t}$
). The existence of such a set B is by a simple generalisation of Behrend’s construction [
Reference Behrend3
] of sets avoiding 3-term arithmetic progressions, see [Reference Alon1, lemma 3·1]. Take pairwise-disjoint sets
$y_1=y_2=\cdots=y_{t}$
). The existence of such a set B is by a simple generalisation of Behrend’s construction [
Reference Behrend3
] of sets avoiding 3-term arithmetic progressions, see [Reference Alon1, lemma 3·1]. Take pairwise-disjoint sets
![]() $V_1,\ldots,V_{t}$
of size n each, and identify each
$V_1,\ldots,V_{t}$
of size n each, and identify each
![]() $V_i$
with [n]. For each
$V_i$
with [n]. For each
![]() $x \in [n/t]$
and
$x \in [n/t]$
and
![]() $y \in B$
, add to G a canonical copy
$y \in B$
, add to G a canonical copy
![]() $S_{x,y}$
of
$S_{x,y}$
of
![]() $C_{t}$
on the vertices
$C_{t}$
on the vertices
![]() $v_i = x + (i - 1)y \in V_i$
,
$v_i = x + (i - 1)y \in V_i$
,
![]() $i = 1,\ldots,t$
. Note that
$i = 1,\ldots,t$
. Note that
![]() $x + (i - 1)y \leq x + (t-1)y \leq n$
, so
$x + (i - 1)y \leq x + (t-1)y \leq n$
, so
![]() $v_i$
indeed “fits” into
$v_i$
indeed “fits” into
![]() $V_i = [n]$
. The copies
$V_i = [n]$
. The copies
![]() $S_{x,y}$
(where
$S_{x,y}$
(where
![]() $x \in [n/t], y \in B$
) are 2-disjoint. Indeed, if
$x \in [n/t], y \in B$
) are 2-disjoint. Indeed, if
![]() $S_{x_1,y_1},S_{x_2,y_2}$
intersect in
$S_{x_1,y_1},S_{x_2,y_2}$
intersect in
![]() $V_i$
and in
$V_i$
and in
![]() $V_j$
, then
$V_j$
, then
![]() $x_1 + (i - 1)y_1 = x_2 + (i - 1)y_2$
and
$x_1 + (i - 1)y_1 = x_2 + (i - 1)y_2$
and
![]() $x_1 + (j - 1)y_1 = x_2 + (j - 1)y_2$
, and solving this system of equations gives
$x_1 + (j - 1)y_1 = x_2 + (j - 1)y_2$
, and solving this system of equations gives
![]() $x_1 = x_2, y_1 = y_2$
. The number of copies
$x_1 = x_2, y_1 = y_2$
. The number of copies
![]() $S_{x,y}$
is
$S_{x,y}$
is
![]() ${n}/{t} \cdot |B| \geq n^2/e^{O\sqrt{\log n}}$
.
${n}/{t} \cdot |B| \geq n^2/e^{O\sqrt{\log n}}$
.
Let us bound the total number of canonical copies of
![]() $C_{t}$
in G. Fix a canonical copy with vertices
$C_{t}$
in G. Fix a canonical copy with vertices
![]() $v_1,\ldots,v_{t}$
,
$v_1,\ldots,v_{t}$
,
![]() $v_i \in V_i$
. For
$v_i \in V_i$
. For
![]() $1 \leq j \leq t-1$
, let
$1 \leq j \leq t-1$
, let
![]() $x_j \in [n/t], y_j \in B$
be such that
$x_j \in [n/t], y_j \in B$
be such that
![]() $v_{j},v_{j+1} \in S_{x_j,y_j}$
. Similarly, let
$v_{j},v_{j+1} \in S_{x_j,y_j}$
. Similarly, let
![]() $x_{t} \in [n/t], y_{t} \in B$
such that
$x_{t} \in [n/t], y_{t} \in B$
such that
![]() $v_1,v_{t} \in S_{x_{t},y_{t}}$
. Then we have
$v_1,v_{t} \in S_{x_{t},y_{t}}$
. Then we have
![]() $v_{j+1} - v_{j} = y_j$
for every
$v_{j+1} - v_{j} = y_j$
for every
![]() $1 \leq j \leq t-1$
, and
$1 \leq j \leq t-1$
, and
![]() $v_{t} - v_{1} = (t-1)y_{t}$
. So
$v_{t} - v_{1} = (t-1)y_{t}$
. So
![]() $y_1 + \ldots + y_{t-1} = (t-1)y_{t}$
. By our choice of B, we have
$y_1 + \ldots + y_{t-1} = (t-1)y_{t}$
. By our choice of B, we have
![]() $y_1 = \ldots = y_{t} =: y$
. Now, for each
$y_1 = \ldots = y_{t} =: y$
. Now, for each
![]() $1 \leq j \leq t-1$
we have
$1 \leq j \leq t-1$
we have
![]() $x_j = v_{j+1} - j \cdot y = x_{j+1}$
, so
$x_j = v_{j+1} - j \cdot y = x_{j+1}$
, so
![]() $x_1 = \ldots = x_{t} =: x$
. So we see that the only canonical copies of
$x_1 = \ldots = x_{t} =: x$
. So we see that the only canonical copies of
![]() $C_{t}$
in G are the copies
$C_{t}$
in G are the copies
![]() $S_{x,y}$
. Their number is at most
$S_{x,y}$
. Their number is at most
![]() $n^2 \leq n^{t-1}$
, as required.
$n^2 \leq n^{t-1}$
, as required.
Recall that
![]() $K_{s}^{(s-1)}$
is the
$K_{s}^{(s-1)}$
is the
![]() $(s-1)$
-graph with vertices
$(s-1)$
-graph with vertices
![]() $1,\ldots,s$
and all s possible edges. The following construction appears implicitly in [
Reference Kohayakawa, Nagle and Rödl9
] (see also [
Reference Alon and Shapira2
]). Again, for completeness, we include a proof.
$1,\ldots,s$
and all s possible edges. The following construction appears implicitly in [
Reference Kohayakawa, Nagle and Rödl9
] (see also [
Reference Alon and Shapira2
]). Again, for completeness, we include a proof.
Lemma 2·7.
Let
![]() $s \geq 3$
. For every large enough n, there is an s-partite
$s \geq 3$
. For every large enough n, there is an s-partite
![]() $(s-1)$
-graph G with sides
$(s-1)$
-graph G with sides
![]() $V_1,\ldots,V_s$
, each of size n, such that G has a collection of
$V_1,\ldots,V_s$
, each of size n, such that G has a collection of
![]() $n^{s-1}/e^{O(\sqrt{\log n})} = n^{s-1-o(1)}$
$n^{s-1}/e^{O(\sqrt{\log n})} = n^{s-1-o(1)}$
![]() $(s-1)$
-disjoint canonical copies of
$(s-1)$
-disjoint canonical copies of
![]() $K_{s}^{(s-1)}$
, but at most
$K_{s}^{(s-1)}$
, but at most
![]() $n^{s-1}$
copies of
$n^{s-1}$
copies of
![]() $K_{s}^{(s-1)}$
altogether.
$K_{s}^{(s-1)}$
altogether.
Proof. Take a set
![]() $B \subseteq [n/s]$
,
$B \subseteq [n/s]$
,
![]() $|B| \geq n/e^{O\sqrt{\log n}}$
, with no non-trivial solution to
$|B| \geq n/e^{O\sqrt{\log n}}$
, with no non-trivial solution to
![]() $y_1 + y_2 = 2y_3$
,
$y_1 + y_2 = 2y_3$
,
![]() $y_1,y_2,y_3 \in B$
. Take pairwise-disjoint sets
$y_1,y_2,y_3 \in B$
. Take pairwise-disjoint sets
![]() $V_1,\ldots,V_s$
of size n each, and identify each
$V_1,\ldots,V_s$
of size n each, and identify each
![]() $V_i$
with [n]. For each
$V_i$
with [n]. For each
![]() $x_1,\ldots,x_{s-2} \in [n/s]$
and
$x_1,\ldots,x_{s-2} \in [n/s]$
and
![]() $y \in B$
, add to G a copy
$y \in B$
, add to G a copy
![]() $K_{x_1,\ldots,x_{s-2},y}$
of
$K_{x_1,\ldots,x_{s-2},y}$
of
![]() $K_s^{(s-1)}$
on the vertices
$K_s^{(s-1)}$
on the vertices
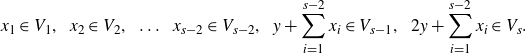 $$ x_1 \in V_1, \,\,\,x_2 \in V_2, \,\,\,\ldots \,\,\,x_{s-2} \in V_{s-2}, \,\,\,y+\sum^{s-2}_{i=1}x_i \in V_{s-1}, \,\,\,2y+\sum^{s-2}_{i=1}x_i \in V_s.$$
$$ x_1 \in V_1, \,\,\,x_2 \in V_2, \,\,\,\ldots \,\,\,x_{s-2} \in V_{s-2}, \,\,\,y+\sum^{s-2}_{i=1}x_i \in V_{s-1}, \,\,\,2y+\sum^{s-2}_{i=1}x_i \in V_s.$$
It is easy to see that these copies are
![]() $(s-1)$
-disjoint, because fixing any
$(s-1)$
-disjoint, because fixing any
![]() $s-1$
of the s coordinates allows to solve for
$s-1$
of the s coordinates allows to solve for
![]() $x_1,\ldots,x_{s-2},y$
. Also, the number of copies thus placed is
$x_1,\ldots,x_{s-2},y$
. Also, the number of copies thus placed is
![]() $(n/s)^{s-2} \cdot |B| \geq n^{s-1}/e^{O\sqrt{\log n}}$
. Let us show that there are no other copies of
$(n/s)^{s-2} \cdot |B| \geq n^{s-1}/e^{O\sqrt{\log n}}$
. Let us show that there are no other copies of
![]() $K_s^{(s-1)}$
in G. This would imply that the total number of copies of
$K_s^{(s-1)}$
in G. This would imply that the total number of copies of
![]() $K_s^{(s-1)}$
in G is
$K_s^{(s-1)}$
in G is
![]() $(n/s)^{s-2} \cdot |B| \leq n^{s-1}$
. So suppose that
$(n/s)^{s-2} \cdot |B| \leq n^{s-1}$
. So suppose that
![]() $v_1 \in V_1,\ldots,v_s \in V_s$
form a copy of
$v_1 \in V_1,\ldots,v_s \in V_s$
form a copy of
![]() $K_s^{(s-1)}$
. Let
$K_s^{(s-1)}$
. Let
![]() $x^{(i)} = (x^{(i)}_1,\ldots,x^{(i)}_{s-2}) \in [n/s]^{s-2}$
and
$x^{(i)} = (x^{(i)}_1,\ldots,x^{(i)}_{s-2}) \in [n/s]^{s-2}$
and
![]() $y_i \in B$
,
$y_i \in B$
,
![]() $i = 1,2,3$
, be such that
$i = 1,2,3$
, be such that
![]() $\{v_2,\ldots,v_s\} \in K_{x^{(1)},y_1}$
,
$\{v_2,\ldots,v_s\} \in K_{x^{(1)},y_1}$
,
![]() $\{v_1,\ldots,v_{s-1}\} \in K_{x^{(2)},y_2}$
and
$\{v_1,\ldots,v_{s-1}\} \in K_{x^{(2)},y_2}$
and
![]() $\{v_1,\ldots,v_{s-2},v_s\} \in K_{x^{(3)},y_3}$
. Then
$\{v_1,\ldots,v_{s-2},v_s\} \in K_{x^{(3)},y_3}$
. Then
![]() $x^{(2)}_1 = x^{(3)}_1 = v_1$
and
$x^{(2)}_1 = x^{(3)}_1 = v_1$
and
Also,
![]() $v_s - v_{s-1} = y_1$
,
$v_s - v_{s-1} = y_1$
,
![]() $v_{s-1} - v_1 = x^{(2)}_2 + \cdots + x^{(2)}_{s-2} + y_2$
and
$v_{s-1} - v_1 = x^{(2)}_2 + \cdots + x^{(2)}_{s-2} + y_2$
and
![]() $v_s - v_1 = x^{(3)}_2 + \cdots + x^{(3)}_{s-2} + 2y_3$
. Combining these three equations and using (2
$v_s - v_1 = x^{(3)}_2 + \cdots + x^{(3)}_{s-2} + 2y_3$
. Combining these three equations and using (2
![]() $ \cdot $
2), we get
$ \cdot $
2), we get
![]() $y_1 + y_2 = 2y_3$
, and so
$y_1 + y_2 = 2y_3$
, and so
![]() $y_1 = y_2 = y_3 =: y$
by our choice of B. Also,
$y_1 = y_2 = y_3 =: y$
by our choice of B. Also,
![]() $x^{(1)}_1 = v_{s-1} - (v_2 + \cdots + v_{s-2} + y) = x^{(2)}_1$
. So
$x^{(1)}_1 = v_{s-1} - (v_2 + \cdots + v_{s-2} + y) = x^{(2)}_1$
. So
![]() $x^{(1)} = x^{(2)} = x^{(3)}$
.
$x^{(1)} = x^{(2)} = x^{(3)}$
.
We now prove two lemmas, Lemmas 2·8 and 2·9, which imply Lemmas 1·1 and 1·2, respectively. Recall that for a k-graph F and
![]() $2 \leq \ell \leq k$
, the
$2 \leq \ell \leq k$
, the
![]() $\ell$
-shadow of F, denoted
$\ell$
-shadow of F, denoted
![]() $\partial_{\ell}F$
, is the
$\partial_{\ell}F$
, is the
![]() $\ell$
-graph consisting of all
$\ell$
-graph consisting of all
![]() $f \in \binom{V(F)}{\ell}$
such that there is
$f \in \binom{V(F)}{\ell}$
such that there is
![]() $e \in E(F)$
with
$e \in E(F)$
with
![]() $f \subseteq e$
.
$f \subseteq e$
.
Lemma 2·8.
Let
![]() $k \geq 2$
, let F be a core k-graph, and suppose that
$k \geq 2$
, let F be a core k-graph, and suppose that
![]() $\partial_2 F$
has an induced cycle of length at least 4. Then for every large enough n there is a k-graph H with
$\partial_2 F$
has an induced cycle of length at least 4. Then for every large enough n there is a k-graph H with
![]() $v(F) \cdot n$
vertices which is homomorphic to F, has a collection of
$v(F) \cdot n$
vertices which is homomorphic to F, has a collection of
![]() $n^k/e^{O(\sqrt{\log n})} = n^{k-o(1)}$
edge-disjoint copies of F, but has at most
$n^k/e^{O(\sqrt{\log n})} = n^{k-o(1)}$
edge-disjoint copies of F, but has at most
![]() $n^{v(F) - 1}$
copies of F altogether.
$n^{v(F) - 1}$
copies of F altogether.
Proof. It will be convenient to write
![]() $|V(F)| = t+r$
and assume that
$|V(F)| = t+r$
and assume that
![]() $V(F) = [t+r]$
, where
$V(F) = [t+r]$
, where
![]() $(1,2,\ldots,t,1)$
is an induced cycle in
$(1,2,\ldots,t,1)$
is an induced cycle in
![]() $\partial_2 F$
and
$\partial_2 F$
and
![]() $t \geq 4$
. It follows that
$t \geq 4$
. It follows that
![]() $|e \cap \{1,\ldots,t\}| \leq 2$
for every
$|e \cap \{1,\ldots,t\}| \leq 2$
for every
![]() $e \in E(F)$
. Take disjoint sets
$e \in E(F)$
. Take disjoint sets
![]() $V_1,\ldots,V_{t+r}$
of size n each. Let G be the t-partite graph with sides
$V_1,\ldots,V_{t+r}$
of size n each. Let G be the t-partite graph with sides
![]() $V_1,\ldots,V_t$
given by Lemma 2·6. Let
$V_1,\ldots,V_t$
given by Lemma 2·6. Let
![]() $\mathcal{S}$
be a collection of
$\mathcal{S}$
be a collection of
![]() $n^2/e^{O(\sqrt{\log n})}$
2-disjoint canonical copies of
$n^2/e^{O(\sqrt{\log n})}$
2-disjoint canonical copies of
![]() $C_t$
in G. Apply Lemma 2·3 toFootnote
4
$C_t$
in G. Apply Lemma 2·3 toFootnote
4
![]() $\mathcal{S}$
with
$\mathcal{S}$
with
![]() $s=t$
and
$s=t$
and
![]() $\ell = 2$
to obtain a family
$\ell = 2$
to obtain a family
![]() $\mathcal{F} \subseteq V_1 \times \ldots \times V_{t+r}$
satisfying Items 1-3 in that lemma. Note that
$\mathcal{F} \subseteq V_1 \times \ldots \times V_{t+r}$
satisfying Items 1-3 in that lemma. Note that
![]() $r \geq k-2 = k-\ell$
, because each edge of F contains at most two vertices from
$r \geq k-2 = k-\ell$
, because each edge of F contains at most two vertices from
![]() $\{1,\ldots,t\}$
and hence at least
$\{1,\ldots,t\}$
and hence at least
![]() $k-2$
vertices from
$k-2$
vertices from
![]() $\{t+1,\ldots,t+r\}$
. Therefore, the conditions of Lemma 2·3 are satisfied. Define the hypergraph H by placing a canonical copy of F on each
$\{t+1,\ldots,t+r\}$
. Therefore, the conditions of Lemma 2·3 are satisfied. Define the hypergraph H by placing a canonical copy of F on each
![]() $F' \in \mathcal{F}$
. We claim that these copies of F are edge-disjoint. Indeed, suppose by contradiction that the copies on
$F' \in \mathcal{F}$
. We claim that these copies of F are edge-disjoint. Indeed, suppose by contradiction that the copies on
![]() $F_1,F_2 \in \mathcal{F}$
share an edge e. Then
$F_1,F_2 \in \mathcal{F}$
share an edge e. Then
![]() $|F_1 \cap F_2| \geq k$
. By Lemma 2·3(iii), we have
$|F_1 \cap F_2| \geq k$
. By Lemma 2·3(iii), we have
![]() $\#\{t+1 \leq i \leq t+r\,:\,F_1(i) = F_2(i)\} \leq k-3$
. This implies that
$\#\{t+1 \leq i \leq t+r\,:\,F_1(i) = F_2(i)\} \leq k-3$
. This implies that
![]() $\#\{1 \leq i \leq t\,:\,e \cap V_i \neq \emptyset\} \geq 3$
. But this means that in F there is an edge which intersects
$\#\{1 \leq i \leq t\,:\,e \cap V_i \neq \emptyset\} \geq 3$
. But this means that in F there is an edge which intersects
![]() $\{1,\ldots,t\}$
in at least 3 vertices, a contradiction. So the F-copies in
$\{1,\ldots,t\}$
in at least 3 vertices, a contradiction. So the F-copies in
![]() $\mathcal{F}$
are indeed edge-disjoint. Their number is
$\mathcal{F}$
are indeed edge-disjoint. Their number is
![]() $|\mathcal{F}| \geq \Omega(|\mathcal{S}|n^{k-2}) \geq n^k/e^{O(\sqrt{\log n})}$
, by Lemma 2·3(ii).
$|\mathcal{F}| \geq \Omega(|\mathcal{S}|n^{k-2}) \geq n^k/e^{O(\sqrt{\log n})}$
, by Lemma 2·3(ii).
To complete the proof, it remains to show that H has at most
![]() $n^{t+r-1}$
copies of F. Observe that H is homomorphic to F; indeed, the map
$n^{t+r-1}$
copies of F. Observe that H is homomorphic to F; indeed, the map
![]() $\varphi$
which sends
$\varphi$
which sends
![]() $V_j \mapsto j$
,
$V_j \mapsto j$
,
![]() $j = 1,\ldots,t+r$
, is such a homomorphism. Let
$j = 1,\ldots,t+r$
, is such a homomorphism. Let
![]() $F^*$
be a copy of F in H. Since F is a core and
$F^*$
be a copy of F in H. Since F is a core and
![]() $\varphi$
is a homomorphism from H to F, we can apply Claim 2·2 to conclude that
$\varphi$
is a homomorphism from H to F, we can apply Claim 2·2 to conclude that
![]() $F^*$
must have the form
$F^*$
must have the form
![]() $v_1,\ldots,v_{t+r}$
, with
$v_1,\ldots,v_{t+r}$
, with
![]() $v_i \in V_i$
playing the role of i for each
$v_i \in V_i$
playing the role of i for each
![]() $i = 1,\ldots,t+r$
. We claim that
$i = 1,\ldots,t+r$
. We claim that
![]() $v_1,\ldots,v_t$
form a canonical copy of
$v_1,\ldots,v_t$
form a canonical copy of
![]() $C_t$
in
Footnote
5
G. To see this, fix any
$C_t$
in
Footnote
5
G. To see this, fix any
![]() $1 \leq i \leq t$
and let us show that
$1 \leq i \leq t$
and let us show that
![]() $\{v_i,v_{i+1}\} \in E(G)$
, with indices taken modulo t. Since
$\{v_i,v_{i+1}\} \in E(G)$
, with indices taken modulo t. Since
![]() $\{i,i+1\}$
is an edge of
$\{i,i+1\}$
is an edge of
![]() $\partial_2 F$
, there must be an edge
$\partial_2 F$
, there must be an edge
![]() $e \in E(F)$
containing
$e \in E(F)$
containing
![]() $i,i+1$
. Then
$i,i+1$
. Then
![]() $\{v_a\,:\,a \in e\} \in E(F^*) \subseteq E(H) = \bigcup_{F' \in \mathcal{F}}{E(F')}$
. Let
$\{v_a\,:\,a \in e\} \in E(F^*) \subseteq E(H) = \bigcup_{F' \in \mathcal{F}}{E(F')}$
. Let
![]() $F' \in \mathcal{F}$
such that
$F' \in \mathcal{F}$
such that
![]() $\{v_a\,:\,a \in e\} \in E(F')$
. By Lemma 2·3(i), we have
$\{v_a\,:\,a \in e\} \in E(F')$
. By Lemma 2·3(i), we have
![]() $S' := F'|_{V_1 \times \ldots \times V_t} \in \mathcal{S}$
. Now,
$S' := F'|_{V_1 \times \ldots \times V_t} \in \mathcal{S}$
. Now,
![]() $S'$
is the vertex set of a canonical copy of
$S'$
is the vertex set of a canonical copy of
![]() $C_t$
in G, and hence
$C_t$
in G, and hence
![]() $\{v_i,v_{i+1}\} \in E(G)$
, as required. This proves our claim that
$\{v_i,v_{i+1}\} \in E(G)$
, as required. This proves our claim that
![]() $v_1,\ldots,v_t$
form a canonical copy of
$v_1,\ldots,v_t$
form a canonical copy of
![]() $C_t$
in G. Summarising, every copy of F in H contains the vertices of a canonical copy of
$C_t$
in G. Summarising, every copy of F in H contains the vertices of a canonical copy of
![]() $C_t$
in G. By the guarantees of Lemma 2·6, the number of canonical copies of
$C_t$
in G. By the guarantees of Lemma 2·6, the number of canonical copies of
![]() $C_t$
in G is at most
$C_t$
in G is at most
![]() $n^{t-1}$
. Hence, the number of copies of F in H is at most
$n^{t-1}$
. Hence, the number of copies of F in H is at most
![]() $n^{t-1} \cdot n^{r} = n^{t+r-1}$
, as required.
$n^{t-1} \cdot n^{r} = n^{t+r-1}$
, as required.
Lemma 2·9.
Let
![]() $k \geq 2$
, let F be a core k-graph and suppose that there are
$k \geq 2$
, let F be a core k-graph and suppose that there are
![]() $3 \leq s \leq k + 1$
and a set
$3 \leq s \leq k + 1$
and a set
![]() $I \subseteq V(F)$
such that
$I \subseteq V(F)$
such that
![]() $(\partial_{s-1} F)[I] \cong K_s^{(s-1)}$
and
$(\partial_{s-1} F)[I] \cong K_s^{(s-1)}$
and
![]() $|e \cap I| \leq s-1$
for every
$|e \cap I| \leq s-1$
for every
![]() $e \in E(F)$
. Then for every large enough n there is a k-graph H with
$e \in E(F)$
. Then for every large enough n there is a k-graph H with
![]() $v(F) \cdot n$
vertices which is homomorphic to F, has a collection of
$v(F) \cdot n$
vertices which is homomorphic to F, has a collection of
![]() $n^k/e^{O(\sqrt{\log n})} = n^{k-o(1)}$
edge-disjoint copies of F, but has at most
$n^k/e^{O(\sqrt{\log n})} = n^{k-o(1)}$
edge-disjoint copies of F, but has at most
![]() $n^{v(F) - 1}$
copies of F altogether.
$n^{v(F) - 1}$
copies of F altogether.
Proof. The proof is very similar to that of Lemma 2·8. Assume that
![]() $I = [s]$
,
$I = [s]$
,
![]() $V(F) = [s+r]$
. Take disjoint sets
$V(F) = [s+r]$
. Take disjoint sets
![]() $V_1,\ldots,V_{s+r}$
of size n each. Let G be the s-partite
$V_1,\ldots,V_{s+r}$
of size n each. Let G be the s-partite
![]() $(s-1)$
-graph with sides
$(s-1)$
-graph with sides
![]() $V_1,\ldots,V_s$
given by Lemma 2·7. Let
$V_1,\ldots,V_s$
given by Lemma 2·7. Let
![]() $\mathcal{S}$
be a collection of
$\mathcal{S}$
be a collection of
![]() $n^{s-1}/e^{O(\sqrt{\log n})}$
$n^{s-1}/e^{O(\sqrt{\log n})}$
![]() $(s-1)$
-disjoint copies of
$(s-1)$
-disjoint copies of
![]() $K_{s}^{(s-1)}$
in G. Apply Lemma 2·3 to
$K_{s}^{(s-1)}$
in G. Apply Lemma 2·3 to
![]() $\mathcal{S}$
with
$\mathcal{S}$
with
![]() $\ell = s-1$
to obtain a family
$\ell = s-1$
to obtain a family
![]() $\mathcal{F} \subseteq V_1 \times \ldots \times V_{s+r}$
satisfying (i)-(iii) in that lemma. Define the hypergraph H by placing a canonical copy of F on each
$\mathcal{F} \subseteq V_1 \times \ldots \times V_{s+r}$
satisfying (i)-(iii) in that lemma. Define the hypergraph H by placing a canonical copy of F on each
![]() $F' \in \mathcal{F}$
. These copies of F are edge-disjoint. Indeed, suppose by contradiction that the copies on
$F' \in \mathcal{F}$
. These copies of F are edge-disjoint. Indeed, suppose by contradiction that the copies on
![]() $F_1,F_2 \in \mathcal{F}$
share an edge e. Then
$F_1,F_2 \in \mathcal{F}$
share an edge e. Then
![]() $|F_1 \cap F_2| \geq k$
, and hence
$|F_1 \cap F_2| \geq k$
, and hence
![]() $\#\{s+1 \leq i \leq s+r\,:\,F_1(i) = F_2(i)\} \leq k-\ell-1 = k-s$
by Lemma 2·3(iii). But then
$\#\{s+1 \leq i \leq s+r\,:\,F_1(i) = F_2(i)\} \leq k-\ell-1 = k-s$
by Lemma 2·3(iii). But then
![]() $\#\{1 \leq i \leq s\,:\,e \cap V_i \neq \emptyset\} = s$
, meaning that there is an edge of F which contains
$\#\{1 \leq i \leq s\,:\,e \cap V_i \neq \emptyset\} = s$
, meaning that there is an edge of F which contains
![]() $I = [s]$
, a contradiction to the assumption of the lemma. So the F-copies in
$I = [s]$
, a contradiction to the assumption of the lemma. So the F-copies in
![]() $\mathcal{F}$
are indeed edge-disjoint. Also,
$\mathcal{F}$
are indeed edge-disjoint. Also,
![]() $|\mathcal{F}| \geq \Omega(|\mathcal{S}|n^{k-s+1}) \geq n^k/e^{O(\sqrt{\log n})}$
, using Lemma 2·3(ii).
$|\mathcal{F}| \geq \Omega(|\mathcal{S}|n^{k-s+1}) \geq n^k/e^{O(\sqrt{\log n})}$
, using Lemma 2·3(ii).
The map
![]() $V_j \mapsto j$
,
$V_j \mapsto j$
,
![]() $j = 1,\ldots,s+r$
is a homomorphism from H to F. Let us bound the number of copies of F in H. By Claim 2·2, every copy
$j = 1,\ldots,s+r$
is a homomorphism from H to F. Let us bound the number of copies of F in H. By Claim 2·2, every copy
![]() $F^*$
of F must be of the form
$F^*$
of F must be of the form
![]() $v_1,\ldots,v_{s+r}$
, with
$v_1,\ldots,v_{s+r}$
, with
![]() $v_i \in V_i$
playing the role of i for each
$v_i \in V_i$
playing the role of i for each
![]() $i = 1,\ldots,s+r$
. We claim that
$i = 1,\ldots,s+r$
. We claim that
![]() $v_1,\ldots,v_s$
span a copy of
$v_1,\ldots,v_s$
span a copy of
![]() $K_s^{(s-1)}$
in G. So let
$K_s^{(s-1)}$
in G. So let
![]() $J \in \binom{[s]}{s-1}$
. Since
$J \in \binom{[s]}{s-1}$
. Since
![]() $(\partial_{s-1} F)[I] \cong K_s^{(s-1)}$
, there is an edge
$(\partial_{s-1} F)[I] \cong K_s^{(s-1)}$
, there is an edge
![]() $e \in E(F)$
with
$e \in E(F)$
with
![]() $J \subseteq e$
. Since
$J \subseteq e$
. Since
![]() $F^*$
is a canonical copy of F, we have
$F^*$
is a canonical copy of F, we have
![]() $\{v_i\,:\,i \in e\} \in E(F^*) \subseteq E(H) = \bigcup_{F' \in \mathcal{F}}{E(F')}$
. Let
$\{v_i\,:\,i \in e\} \in E(F^*) \subseteq E(H) = \bigcup_{F' \in \mathcal{F}}{E(F')}$
. Let
![]() $F' \in \mathcal{F}$
be such that
$F' \in \mathcal{F}$
be such that
![]() $\{v_i\,:\,i \in e\} \in E(F')$
. By Lemma 2·3(i), we have
$\{v_i\,:\,i \in e\} \in E(F')$
. By Lemma 2·3(i), we have
![]() $S' := F'|_{V_1 \times \ldots \times V_s} \in \mathcal{S}$
. Now,
$S' := F'|_{V_1 \times \ldots \times V_s} \in \mathcal{S}$
. Now,
![]() $S'$
is a canonical copy of
$S'$
is a canonical copy of
![]() $K_s^{(s-1)}$
in G, and hence
$K_s^{(s-1)}$
in G, and hence
![]() $\{v_i\,:\,i \in J\} \in E(G)$
, as required. So we see that every copy of F in H contains the vertices of a copy of
$\{v_i\,:\,i \in J\} \in E(G)$
, as required. So we see that every copy of F in H contains the vertices of a copy of
![]() $K_s^{(s-1)}$
in G. By the guarantees of Lemma 2·6, G has at most
$K_s^{(s-1)}$
in G. By the guarantees of Lemma 2·6, G has at most
![]() $n^{s-1}$
copies of
$n^{s-1}$
copies of
![]() $K_s^{(s-1)}$
. Hence, H has at most
$K_s^{(s-1)}$
. Hence, H has at most
![]() $n^{s-1} \cdot n^{r} = n^{s+r-1}$
copies of F, as required.
$n^{s-1} \cdot n^{r} = n^{s+r-1}$
copies of F, as required.
Observe that Lemma 1·1 follows by combining Lemmas 2·5 and 2·8. Let us prove Lemma 1·2.
Proof of Lemma 1·2. Let X be a clique of size
![]() $k+1$
in
$k+1$
in
![]() $\partial_2 F$
. Let I be a smallest subset of X which is not contained in an edge of F. Note that I is well-defined (because X itself is not contained in any edge of F, as
$\partial_2 F$
. Let I be a smallest subset of X which is not contained in an edge of F. Note that I is well-defined (because X itself is not contained in any edge of F, as
![]() $|X| = k+1$
). Also,
$|X| = k+1$
). Also,
![]() $|I| \geq 3$
because every pair of vertices in X is contained in some edge, as X is a clique in
$|I| \geq 3$
because every pair of vertices in X is contained in some edge, as X is a clique in
![]() $\partial_2F$
. Put
$\partial_2F$
. Put
![]() $s = |I|$
. Then
$s = |I|$
. Then
![]() $(\partial_{s-1}F)[I] \cong K_s^{(s-1)}$
and
$(\partial_{s-1}F)[I] \cong K_s^{(s-1)}$
and
![]() $|e \cap I| \leq s-1$
for every
$|e \cap I| \leq s-1$
for every
![]() $e \in E(F)$
, by the choice of I. Now the assertion of Lemma 1·2 follows by combining Lemmas 2·5 and 2·9.
$e \in E(F)$
, by the choice of I. Now the assertion of Lemma 1·2 follows by combining Lemmas 2·5 and 2·9.