Refine listing
Actions for selected content:
341 results in 22Exx
Lifting of characters on p-adic orthogonal and metaplectic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 18 March 2010, pp. 795-810
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
The unitary spherical spectrum for split classical groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 16 February 2010, pp. 265-356
- Print publication:
- April 2010
-
- Article
- Export citation
An Algebraic Approach to Weakly Symmetric Finsler Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 52-73
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
The Langlands Correspondence on the Generic Irreducible Constituents of Principal Series
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 94-108
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
VARIANTS OF MIYACHI’S THEOREM FOR NILPOTENT LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 19 January 2010, pp. 1-17
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
On some modular representations of the Borel subgroup of GL2(Qp)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 58-80
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
Regular and residual Eisenstein series and the automorphic cohomology of Sp(2,2)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 23 November 2009, pp. 21-57
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
Whittaker unitary dual of affine graded Hecke algebras of type E
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1563-1616
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
On the equations for universal torsors over del Pezzo surfaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 203-223
- Print publication:
- January 2010
-
- Article
- Export citation
Poles of L-functions and theta liftings for orthogonal groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 10 June 2009, pp. 693-741
- Print publication:
- October 2009
-
- Article
- Export citation
Klyachko Models for General Linear Groups of Rank 5 over a p-Adic Field
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 222-240
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
Algorithms for representation theory of real reductive groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 06 January 2009, pp. 209-259
- Print publication:
- April 2009
-
- Article
- Export citation
Geometric Weil representation: local field case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 56-88
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
Analytic vectors in continuous p-adic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 247-270
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
Genericity of supercuspidal representations of p-adic Sp4
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 213-246
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
(GLn+1(F), GLn(F)) is a Gelfand pair for any local field F
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1504-1524
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
OPERATOR KERNELS FOR IRREDUCIBLE REPRESENTATIONS OF EXPONENTIAL LIE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 301-316
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Adiabatic limit of the eta invariant over cofinite quotients of PSL(2, ℝ)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 26 September 2008, pp. 1593-1616
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
On the classification of rank-two representations of quasiprojective fundamental groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1271-1331
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
On the unramified spectrum of spherical varieties over p-adic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 978-1016
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
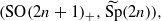 where
where 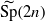 is the metaplectic cover of the symplectic group
is the metaplectic cover of the symplectic group 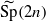 if their characters on corresponding conjugacy classes are equal up to a transfer factor. We study properties of this transfer factor, which is essentially the character of the difference of the two halves of the oscillator representation. We show that the lifting commutes with parabolic induction. These results were motivated by the paper ‘Lifting of characters on orthogonal and metaplectic groups’ by Adams who considered the case
if their characters on corresponding conjugacy classes are equal up to a transfer factor. We study properties of this transfer factor, which is essentially the character of the difference of the two halves of the oscillator representation. We show that the lifting commutes with parabolic induction. These results were motivated by the paper ‘Lifting of characters on orthogonal and metaplectic groups’ by Adams who considered the case 


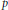

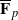 -representation
-representation 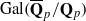 by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(
by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(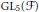
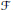
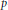
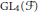
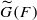 . This is a category of certain perverse sheaves on some stack, on which
. This is a category of certain perverse sheaves on some stack, on which 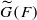 acts by functors. This construction will be used by Lysenko (in [
acts by functors. This construction will be used by Lysenko (in [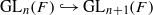 and the two-sided action of GL
and the two-sided action of GL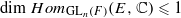 . For the proof in the archimedean case, we develop several tools to study invariant distributions on smooth manifolds.
. For the proof in the archimedean case, we develop several tools to study invariant distributions on smooth manifolds.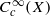 are in natural ‘almost bijection’ with a number of copies of
are in natural ‘almost bijection’ with a number of copies of 