Refine listing
Actions for selected content:
341 results in 22Exx
The Plancherel formula for the horocycle space and generalizations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 42-56
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
Weighted p-Sidon sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-95
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
Characterization of lipschitz spaces on compact Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 200-209
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
On the component group of the automorphism group of a Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-385
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
Subelliptic operators on Lie groups: regularity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-229
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
Lp-functions satisfying the mean value property on homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 384-390
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Harmonic analysis for groups acting on triangle buildings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-383
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
On the Fourier transform of a compact semisimple Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-116
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
Gevrey spaces and their intersections
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 263-286
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
A note on Riesz sets and lacunary sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 57-65
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
The arithmetic structure of tetrahedral groups of hyperbolic isometries
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 221-240
- Print publication:
- December 1989
-
- Article
- Export citation
A qualitative uncertainty principle for semisimple Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 127-132
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
Hardy-Littlewood maximal functions on some solvable Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-82
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
Motion Groups and Absolutely Convergent Fourier Transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-397
- Print publication:
- December 1987
-
- Article
-
- You have access
- Export citation
Irreducibility of the analytic continuation of the principal series of a free group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-210
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation
The Finsler geometry of groups of isometries of Hilbert Space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 196-222
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
Primitive ideals with bounded approximate units in L1-algebras of exponential lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-420
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Bilinear forms and 2-dimensional cohomology
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-179
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
Projective representations of the infinite orthogonal group
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-121
- Print publication:
- June 1977
-
- Article
- Export citation
Note on a theorem of Weil-Abels
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-187
- Print publication:
- December 1971
-
- Article
- Export citation
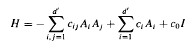
 of
of  be its set of vertices. We study a commutative algebra
be its set of vertices. We study a commutative algebra 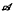 of ‘averaging’ operators acting on the space of complex valued functions on
of ‘averaging’ operators acting on the space of complex valued functions on  is valid. Examples are included.
is valid. Examples are included.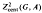 for certain 2-step nilpotent Lie groups
for certain 2-step nilpotent Lie groups 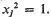
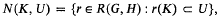
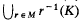 is a relatively compact subset of
is a relatively compact subset of 