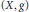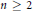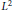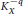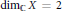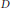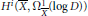Refine listing
Actions for selected content:
476 results in 53Cxx
Notes on contact Ricci solitons
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 47-53
-
- Article
-
- You have access
- Export citation
The Calabi–Yau equation on the Kodaira–Thurston manifold
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 24 September 2010, pp. 437-447
- Print publication:
- April 2011
-
- Article
- Export citation
Greatest lower bounds on the Ricci curvature of Fano manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 August 2010, pp. 319-331
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Gray identities, canonical connection and integrability
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 657-674
-
- Article
-
- You have access
- Export citation
On the quasi-asymptotically locally Euclidean geometry of Nakajima's metric
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 29 June 2010, pp. 119-147
- Print publication:
- January 2011
-
- Article
- Export citation
HOMOGENEOUS AND H-CONTACT UNIT TANGENT SPHERE BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 12 May 2010, pp. 323-337
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
A surface that contains many Lorentzian circles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 293-298
-
- Article
-
- You have access
- Export citation
Homogeneous Kähler and Sasakian structures related to complex hyperbolic spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 393-413
-
- Article
-
- You have access
- Export citation
Complex submanifolds, connections and asymptotics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 373-383
-
- Article
-
- You have access
- Export citation
A MINIMAL REAL HYPERSURFACE OF A COMPLEX PROJECTIVE SPACE WITH NONNEGATIVE SECTIONAL CURVATURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 17 March 2010, pp. 488-492
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
QUADRATIC CURVATURE ENERGIES IN THE 2-SPHERE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 02 March 2010, pp. 496-506
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
An Algebraic Approach to Weakly Symmetric Finsler Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 52-73
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
On the Asymptotic Behavior of Complete Kähler Metrics of Positive Ricci Curvature
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-18
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
MAXIMAL ANNULI WITH PARALLEL PLANAR BOUNDARIES IN THE THREE-DIMENSIONAL LORENTZ–MINKOWSKI SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 27 January 2010, pp. 208-222
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
A C0-estimate for the parabolic Monge–Ampère equation on complete non-compact Kähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 259-270
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
Markov Type of Alexandrov Spaces of Non-Negative Curvature Shin-Ichi Ohta
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 177-189
- Print publication:
- December 2009
-
- Article
- Export citation
REAL HYPERSURFACES WITH CYCLIC-PARALLEL STRUCTURE JACOBI OPERATORS IN A NONFLAT COMPLEX SPACE FORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 21 October 2009, pp. 260-273
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
REILLY INEQUALITIES OF ELLIPTIC OPERATORS ON CLOSED SUBMANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 335-346
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
A CLASSIFICATION OF SPHERICAL SYMMETRIC CR MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 251-274
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
CONVOLUTIONS OF GENERIC ORBITAL MEASURES IN COMPACT SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 05 May 2009, pp. 513-522
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
 is a Riemannian
is a Riemannian 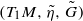 is
is