Refine listing
Actions for selected content:
476 results in 53Cxx
PINCHING THEOREMS FOR A COMPACT MINIMAL SUBMANIFOLD IN A COMPLEX PROJECTIVE SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 99-114
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF HYPERSURFACES OF TYPE A2 IN A COMPLEX PROJECTIVE SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 1-8
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Quaternionic Dolbeault complex and vanishing theorems on hyperkähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1576-1592
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
The Monge-Ampère equation and warped products of higher rank
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-16
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Random motions at finite velocity in a non-Euclidean space
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 588-611
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
On a theorem of Ambrose
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-152
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Principal component analysis for Riemannian manifolds, with an application to triangular shape spaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 299-319
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Twisted complex geometry
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-296
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Constant curved minimal CR 3-spheres in CPn
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-10
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
Electromagnetic wave propagation and inequalities for moments of chord lengths
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 987-995
- Print publication:
- December 2004
-
- Article
- Export citation
An application of Moser iteration to complete minimal submanifolds in a sphere
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 151-166
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Harmonic maps and cosymplectic manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 75-92
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
An integral formula for compact hypersurfaces in space forms and its applications
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 239-248
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Distance measurements on processes of flats
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 70-95
- Print publication:
- March 2003
-
- Article
- Export citation
Naturally reductive homogeneous real hypersurfaces in quaternionic space forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-100
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Determination of the mean normal measure from isotropic means of flat sections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 505-519
- Print publication:
- September 2002
-
- Article
- Export citation
A note on design-based versus model-based variance estimation in stereology
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 484-490
- Print publication:
- September 2002
-
- Article
- Export citation
Variance prediction for pseudosystematic sampling on the sphere
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 469-483
- Print publication:
- September 2002
-
- Article
- Export citation
Ricci curvature of submanifolds in Sasakian space forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 247-256
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
The set covariance of a dead leaves model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 19 February 2016, pp. 11-20
- Print publication:
- March 2002
-
- Article
- Export citation
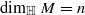 , and
, and 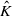 of the dual Kähler cone, then
of the dual Kähler cone, then 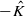 , then
, then 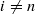 .
.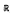
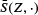 be the mean normal measure of a stationary random set
be the mean normal measure of a stationary random set 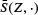 and the mean of
and the mean of 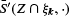 . Here, the mean is understood to be with respect to the random isotropic
. Here, the mean is understood to be with respect to the random isotropic 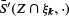 before averaging. A large class of liftings and their resulting means are discussed. In particular, a geometrically motivated lifting is presented, for which the mean of liftings of
before averaging. A large class of liftings and their resulting means are discussed. In particular, a geometrically motivated lifting is presented, for which the mean of liftings of 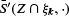 determines
determines 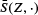 uniquely for any fixed
uniquely for any fixed 