Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Vries, Erik Jan
and
Schroers, Bernd J.
2009.
Supersymmetric quantum mechanics of magnetic monopoles: A case study.
Nuclear Physics B,
Vol. 815,
Issue. 3,
p.
368.
Alesker, S.
and
Verbitsky, M.
2010.
Quaternionic Monge-Ampère equation and Calabi problem for HKT-manifolds.
Israel Journal of Mathematics,
Vol. 176,
Issue. 1,
p.
109.
Verbitsky, Misha
2010.
Hyperkähler Syz Conjecture and Semipositive Line Bundles.
Geometric and Functional Analysis,
Vol. 19,
Issue. 5,
p.
1481.
de Vries, Erik Jan
and
Schroers, Bernd J.
2010.
Supercharges, quantum states and angular momentum for supersymmetric monopoles.
Nuclear Physics B,
Vol. 839,
Issue. 1-2,
p.
157.
FEDORUK, S. A.
IVANOV, E. A.
and
SMILGA, A. V.
2012.
REAL AND COMPLEX SUPERSYMMETRIC d = 1 SIGMA MODELS WITH TORSIONS.
International Journal of Modern Physics A,
Vol. 27,
Issue. 25,
p.
1250146.
GRANTCHAROV, GUEO
and
VERBITSKY, MISHA
2013.
CALIBRATIONS IN HYPER-KÄHLER GEOMETRY.
Communications in Contemporary Mathematics,
Vol. 15,
Issue. 02,
p.
1250060.
Yang, Qilin
2014.
Vanishing Theorems on Compact Hyper-kähler Manifolds.
Geometry,
Vol. 2014,
Issue. ,
p.
1.
Soldatenkov, Andrey
and
Verbitsky, Misha
2015.
Holomorphic Lagrangian Fibrations on Hypercomplex Manifolds.
International Mathematics Research Notices,
Vol. 2015,
Issue. 4,
p.
981.
Moore, Gregory W.
Royston, Andrew B.
and
Van den Bleeken, Dieter
2016.
Semiclassical framed BPS states.
Journal of High Energy Physics,
Vol. 2016,
Issue. 7,
Grantcharov, Gueo
Lejmi, Mehdi
and
Verbitsky, Misha
2017.
Existence of HKT metrics on hypercomplex manifolds of real dimension 8.
Advances in Mathematics,
Vol. 320,
Issue. ,
p.
1135.
Amerik, Ekaterina
and
Verbitsky, Misha
2017.
Construction of automorphisms of hyperkähler manifolds.
Compositio Mathematica,
Vol. 153,
Issue. 8,
p.
1610.
Wang, Wei
2018.
On quaternionic complexes over unimodular quaternionic manifolds.
Differential Geometry and its Applications,
Vol. 58,
Issue. ,
p.
227.
Anella, F.
and
Huybrechts, D.
2022.
Effectivity of Semi-positive Line Bundles.
Milan Journal of Mathematics,
Vol. 90,
Issue. 2,
p.
389.
Gorginyan, Yulia
2023.
Complex curves in hypercomplex nilmanifolds with H-solvable Lie algebras.
Journal of Geometry and Physics,
Vol. 192,
Issue. ,
p.
104900.
Meazzini, Francesco
and
Onorati, Claudio
2023.
Hyper-holomorphic connections on vector bundles on hyper-Kähler manifolds.
Mathematische Zeitschrift,
Vol. 303,
Issue. 1,
Dinew, Sławomir
and
Sroka, Marcin
2023.
On the Alesker-Verbitsky Conjecture on HyperKähler Manifolds.
Geometric and Functional Analysis,
Vol. 33,
Issue. 4,
p.
875.
Baltes, Jonas
2024.
Lefschetz-type theorems for the effective cone on Hyperkähler varieties.
Mathematische Zeitschrift,
Vol. 307,
Issue. 1,
Ríos Ortiz, Ángel David
2024.
Higher Gaussian Maps on K3 Surfaces.
International Mathematics Research Notices,
Vol. 2024,
Issue. 10,
p.
8185.
Leung, NaiChung Conan
and
Yau, YuTung
2024.
Hidden $${\text {Sp}}(1)$$-Symmetry and Brane Quantization on HyperKähler Manifolds.
Communications in Mathematical Physics,
Vol. 405,
Issue. 12,


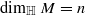 , and
, and 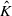 of the dual Kähler cone, then
of the dual Kähler cone, then 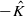 , then
, then 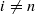 .
.