Refine listing
Actions for selected content:
476 results in 53Cxx
On manifolds with quadratic curvature decay
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 528-540
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Ricci iterations on Kähler classes
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 743-768
- Print publication:
- October 2009
-
- Article
- Export citation
SLANT CURVES IN CONTACT PSEUDO-HERMITIAN 3-MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 383-396
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
IMMERSION OF MANIFOLDS WITH UNBOUNDED IMAGE AND A MODIFIED MAXIMUM PRINCIPLE OF YAU
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 285-291
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
ANTI-COMMUTING REAL HYPERSURFACES IN COMPLEX TWO-PLANE GRASSMANNIANS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 199-210
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
THE ISOPERIMETRIC PROBLEM ON PLANES WITH DENSITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 177-197
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
PARABOLIC AND HYPERBOLIC SCREW MOTION SURFACES IN ℍ2×ℝ
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 113-143
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
HEAT KERNEL BOUNDS, POINCARÉ SERIES, AND L2 SPECTRUM FOR LOCALLY SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 73-86
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Integrating
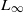 -algebras
-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 1017-1045
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
CONTACT METRIC (κ,μ)-SPACES AS BI-LEGENDRIAN MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 373-386
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
CONTACT AND PANSU DIFFERENTIABLE MAPS ON CARNOT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 495-507
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
A NOTE ON THE UNCLOUDING THE SKY OF NEGATIVELY CURVED MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 413-424
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
The Bochner-flat cone of a CR manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 747-773
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
THREE-FORMS AND ALMOST COMPLEX STRUCTURES ON SIX-DIMENSIONAL MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 247-263
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
ENERGY OF GLOBAL FRAMES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 155-162
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
MEAN-VALUE PROPERTY ON MANIFOLDS WITH MINIMAL HOROSPHERES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 277-282
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
TRANSVERSAL HARMONIC THEORY FOR TRANSVERSALLY SYMPLECTIC FLOWS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 233-245
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
WARPED PRODUCT SEMI-SLANT SUBMANIFOLDS IN LOCALLY RIEMANNIAN PRODUCT MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 177-186
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Estimation of the mean normal measure from flat sections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 31-48
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Supersymmetry of the chiral de Rham complex
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 503-521
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
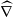 , we construct the parametric equations of Legendre pseudo-Hermitian circles (whose
, we construct the parametric equations of Legendre pseudo-Hermitian circles (whose  -geodesic curvature
-geodesic curvature 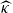 is constant and
is constant and 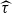 is zero) in
is zero) in  too fast. The main tool in the proof is a modification of Yau’s maximum principle.
too fast. The main tool in the proof is a modification of Yau’s maximum principle. -algebras
-algebras
