Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-25T20:30:43.251Z Has data issue: false hasContentIssue false
  • English
  • Français

Determination of the mean normal measure from isotropic means of flat sections

Part of: Global differential geometry Geometric probability and stochastic geometry

Published online by Cambridge University Press:  01 July 2016

Markus Kiderlen
Markus Kiderlen*
Affiliation:
University of Karlsruhe
*
∗ Postal address: Universität Karlsruhe, Mathematisches Institut II, D-76128 Karlsruhe, Germany. Email address: kiderlen@math.uni-karlsruhe.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 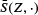be the mean normal measure of a stationary random set Z in the extended convex ring in ℝd. For k ∈ {1,…,d-1}, connections are shown between 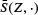and the mean of 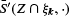. Here, the mean is understood to be with respect to the random isotropic k-dimensional linear subspace ξk and the mean normal measure of the intersection is computed in ξk. This mean to be well defined, a suitable spherical lifting must be applied to 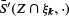before averaging. A large class of liftings and their resulting means are discussed. In particular, a geometrically motivated lifting is presented, for which the mean of liftings of 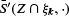determines 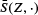uniquely for any fixed k ∈ {2,…,d-1}.

Keywords

Oriented mean normal measurerose of normal directionsspherical liftinglocal Crofton formulaspherical harmonics

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 53C65: Integral geometry
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 34 , Issue 3 , September 2002 , pp. 505 - 519
Copyright
Copyright © Applied Probability Trust 2002 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Fallert, H., Goodey, P. and Weil, W. (1997). Spherical projections and centrally symmetric sets. Adv. Math. 129, 301–322.CrossRefGoogle Scholar
[2] Goodey, P. (1998). Minkowski sums of projections of convex bodies. Mathematika 45, 253–268.Google Scholar
[3] Goodey, P. and Jiang, W. (2000). Minkowski sums of three dimensional projections of convex bodies. Rend. Circ. Mat. Palermo II Suppl. 65, 105–119.Google Scholar
[4] Goodey, P. and Weil, W. (1998). The determination of convex bodies from the mean of random sections. Math. Proc. Camb. Phil. Soc. 112, 419–430.Google Scholar
[5] Goodey, P., Kiderlen, M. and Weil, W. (1998). Section and projection means of convex bodies. Monatshefte Math. 126, 37–54.Google Scholar
[6] Groemer, H. (1996). Geometric Applications of Fourier Series and Spherical Harmonics. Cambridge University Press.Google Scholar
[7] Hilliard, J. E. (1962). Specification and measurement of microstructural anisotropy. Trans. Metall. Soc. AIME 224, 1201–1211.Google Scholar
[8] Hug, D. (2000). Contact distributions of Boolean models. Rend. Circ. Mat. Palermo II Suppl. 65, 137–181.Google Scholar
[9] Hug, D. and Last, G. (2000). On support measures in Minkowski spaces and contact distributions in stochastic geometry. Ann. Prob. 28, 796–850.Google Scholar
[10] Kiderlen, M. (1999). Schnittmittelungen und äquivariante Endomorphismen konvexer Körper. , University of Karlsruhe.Google Scholar
[11] Kiderlen, M. (2001). Non-parametric estimation of the directional distribution of stationary line and fibre processes. Adv. Appl. Prob. 33, 6–24.Google Scholar
[12] Kiderlen, M. (2001). Blaschke and Minkowski endomorphisms of convex bodies. In preparation.Google Scholar
[13] Mecke, J. and Stoyan, D. (1980). Formulas for stationary planar fibre processes I—general theory. Math Operationsforsch. Statist. Ser. Statist. 11, 267–279.Google Scholar
[14] Miles, R. E. (1971). Poisson flats in Euclidean spaces. Part II: Homogeneous Poisson flats and the complementary theorem. Adv. Appl. Prob. 3, 1–43.Google Scholar
[15] Molchanov, I. S. (1995) Statistics of the Boolean model: from the estimation of means to the estimation of distributions. Adv. Appl. Prob. 27, 63–86.Google Scholar
[16] Pohlmann, S., Mecke, J. and Stoyan, D. (1981). Stereological formulas for stationary surface processes. Math. Operationsforsch. Statist. Ser. Statist. 12, 429–440.Google Scholar
[17] Rataj, J. (1996). Estimation of oriented direction distribution of a planar body. Adv. Appl. Prob. 28, 394–404.Google Scholar
[18] Schneider, R. (2001). On the mean normal measure of a particle process. Adv. Appl. Prob. 33, 25–38.CrossRefGoogle Scholar
[19] Schneider, R. and Weil, W. (1992). Integralgeometrie. Teubner, Stuttgart.Google Scholar
[20] Schneider, R. and Weil, W. (2000). Stochastische Geometrie. Teubner, Stuttgart.CrossRefGoogle Scholar
[21] Stoyan, D., Kendall, W. S. and Mecke, J. (1995). Stochastic Geometry and Its Applications, 2nd edn. John Wiley, New York.Google Scholar
[22] Weil, W. (1982). Zonoide und verwandte Klassen konvexer Körper. Monatshefte Math. 94, 73–84.CrossRefGoogle Scholar
[23] Weil, W. (1995). The estimation of mean shape and mean particle number in overlapping particle systems in the plane. Adv. Appl. Prob. 27, 102–119.Google Scholar
[24] Weil, W. (1997). The mean normal distribution of stationary random sets and particle processes. In Advances in the Theory and Applications of Random Sets (Proc. Internat. Symp., Fontainebleau, 1996), ed. Jeulin, D., World Scientific, Singapore, pp. 21–33.Google Scholar
[25] Weil, W. (1997). Mean bodies associated with random closed sets. Rend. Circ. Mat. Palermo II Suppl. 50, 387–412.Google Scholar
[26] Weil, W. (1999). Intensity analysis of Boolean models. Pattern Recognition 32, 1675–1684.Google Scholar
[27] Zähle, M., (1982). Random processes of Hausdorff rectifiable closed sets. Math. Nachr. 108, 49–72.Google Scholar