No CrossRef data available.
Article contents
On the Asymptotic Behavior of Complete Kähler Metrics of Positive Ricci Curvature
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 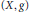 $\left( X,\,g \right)$ be a complete noncompact Kähler manifold, of dimension
$\left( X,\,g \right)$ be a complete noncompact Kähler manifold, of dimension  $n\,\ge \,2$ , with positive Ricci curvature and of standard type (see the definition below). N. Mok proved that
$n\,\ge \,2$ , with positive Ricci curvature and of standard type (see the definition below). N. Mok proved that  $X$ can be compactified, i.e.,
$X$ can be compactified, i.e.,  $X$ is biholomorphic to a quasi-projective variety. The aim of this paper is to prove that the
$X$ is biholomorphic to a quasi-projective variety. The aim of this paper is to prove that the  ${{L}^{2}}$ holomorphic sections of the line bundle
${{L}^{2}}$ holomorphic sections of the line bundle 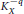 $K_{X}^{-q}$ and the volume form of the metric
$K_{X}^{-q}$ and the volume form of the metric  $g$ have no essential singularities near the divisor at infinity. As a consequence we obtain a comparison between the volume forms of the Kähler metric
$g$ have no essential singularities near the divisor at infinity. As a consequence we obtain a comparison between the volume forms of the Kähler metric  $g$ and of the Fubini-Study metric induced on
$g$ and of the Fubini-Study metric induced on  $X$ . In the case of
$X$ . In the case of  ${{\dim}_{\mathbb{C}}}\,X\,=\,2$ , we establish a relation between the number of components of the divisor
${{\dim}_{\mathbb{C}}}\,X\,=\,2$ , we establish a relation between the number of components of the divisor 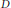 $D$ and the dimension of the
$D$ and the dimension of the 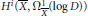 ${{H}^{i}}(\bar{X},\,\Omega \frac{1}{X}(\log \,D))$ .
${{H}^{i}}(\bar{X},\,\Omega \frac{1}{X}(\log \,D))$ .
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010

