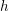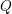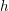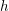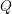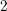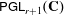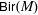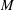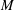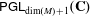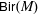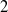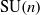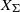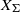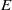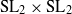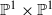Refine listing
Actions for selected content:
145 results in 14Lxx
FROM THE FUNCTION-SHEAF DICTIONARY TO QUASICHARACTERS OF
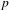 $p$ -ADIC TORI
$p$ -ADIC TORI
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 13 October 2015, pp. 1-37
- Print publication:
- February 2018
-
- Article
- Export citation
Arithmetic of positive characteristic
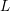 $L$-series values in Tate algebras
$L$-series values in Tate algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 1-61
- Print publication:
- January 2016
-
- Article
- Export citation
Compactifications of reductive groups as moduli stacks of bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 18 August 2015, pp. 62-98
- Print publication:
- January 2016
-
- Article
- Export citation
COX RINGS OF MINIMAL RESOLUTIONS OF SURFACE QUOTIENT SINGULARITIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 325-355
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
The local structure theorem for real spherical varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 09 July 2015, pp. 2145-2159
- Print publication:
- November 2015
-
- Article
- Export citation
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 18 February 2015, pp. 625-671
- Print publication:
- July 2016
-
- Article
- Export citation
Spherical subgroups in simple algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 13 February 2015, pp. 1288-1308
- Print publication:
- July 2015
-
- Article
- Export citation
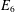 $E_{6}$ AND THE ARITHMETIC OF A FAMILY OF NON-HYPERELLIPTIC CURVES OF GENUS 3
$E_{6}$ AND THE ARITHMETIC OF A FAMILY OF NON-HYPERELLIPTIC CURVES OF GENUS 3
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 12 January 2015, e1
-
- Article
-
- You have access
- Open access
- Export citation
THE DISTRIBUTION OF TORSION SUBSCHEMES OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 15 December 2014, pp. 693-710
- Print publication:
- October 2016
-
- Article
- Export citation
Group schemes and local densities of quadratic lattices in residue characteristic 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 793-827
- Print publication:
- May 2015
-
- Article
- Export citation
On Grothendieck–Serre’s conjecture concerning principal
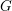 $G$-bundles over reductive group schemes: I
$G$-bundles over reductive group schemes: I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 28 October 2014, pp. 535-567
- Print publication:
- March 2015
-
- Article
- Export citation
Equivariant Compactifications of Two-Dimensional Algebraic Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 149-168
-
- Article
-
- You have access
- Export citation
A study of the representations supported by the orbit closure of the determinant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 292-312
- Print publication:
- February 2015
-
- Article
- Export citation
Hermitian forms over quaternion algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 15 September 2014, pp. 2073-2094
- Print publication:
- December 2014
-
- Article
- Export citation
Morphisms between Cremona groups, and characterization of rational varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 25 June 2014, pp. 1107-1124
- Print publication:
- July 2014
-
- Article
- Export citation
ON THE NILPOTENT SECTION CONJECTURE FOR FINITE GROUP ACTIONS ON CURVES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 13 December 2013, pp. 183-200
- Print publication:
- January 2014
-
- Article
- Export citation
Implosion for hyperkähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 1592-1630
- Print publication:
- September 2013
-
- Article
- Export citation
The arc space of horospherical varieties and motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 19 June 2013, pp. 1327-1352
- Print publication:
- August 2013
-
- Article
- Export citation
Rationality of fields of invariants for some representations ofSL2 × SL2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 22 May 2013, pp. 1225-1234
- Print publication:
- July 2013
-
- Article
- Export citation
On the Iwasawa theory of the Lubin–Tate moduli space
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 793-839
- Print publication:
- May 2013
-
- Article
- Export citation
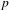
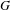
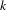
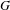
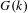
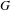
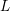
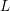
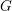
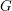
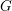
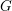
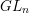
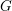
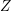
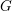
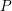
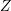
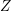
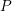
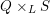
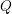
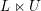
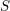
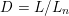
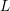
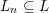
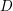

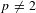
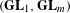
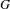
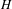

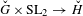
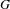
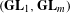
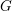

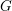
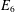

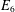
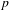
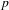




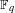
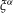

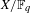

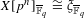
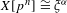
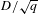
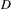


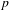

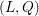
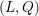
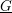
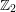
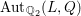
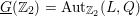
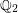
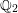
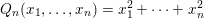
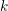
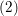
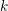
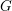
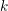
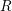
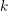
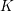
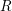
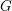
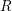
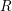
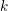
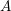
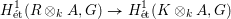
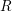
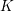
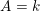
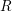
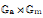 on ℙ
on ℙ