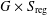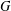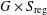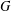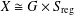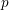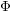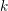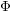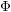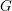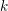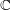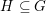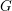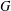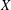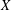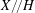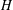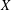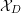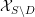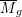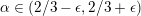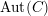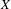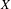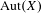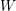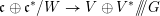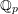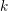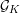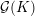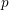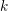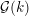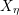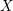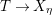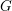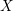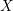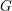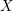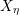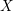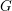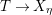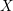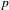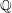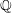Refine listing
Actions for selected content:
145 results in 14Lxx
AN EQUIVARIANT DESCRIPTION OF CERTAIN HOLOMORPHIC SYMPLECTIC VARIETIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 207-214
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
DISPLAYED EQUATIONS FOR GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 13 February 2018, pp. 86-114
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
GROUP ACTION ON THE DEFORMATIONS OF A FORMAL GROUP OVER THE RING OF WITT VECTORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 20 December 2017, pp. 42-57
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
THREE-DIMENSIONAL ISOLATED QUOTIENT SINGULARITIES IN EVEN CHARACTERISTIC
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 435-445
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
On the Popov–Pommerening conjecture for linear algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 36-79
- Print publication:
- January 2018
-
- Article
- Export citation
ON EXISTENCE OF CANONICAL
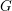 $G$-BASES
$G$-BASES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 15 September 2017, pp. 1-31
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
GRADED UNIPOTENT GROUPS AND GROSSHANS THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 04 September 2017, e21
-
- Article
-
- You have access
- Open access
- Export citation
ON
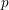 $p$-DIVISIBLE GROUPS WITH SATURATED NEWTON POLYGONS
$p$-DIVISIBLE GROUPS WITH SATURATED NEWTON POLYGONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 07 June 2017, pp. 96-120
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
Second flip in the Hassett–Keel program: a local description
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 18 May 2017, pp. 1547-1583
- Print publication:
- August 2017
-
- Article
- Export citation
Second flip in the Hassett–Keel program: existence of good moduli spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 1584-1609
- Print publication:
- August 2017
-
- Article
- Export citation
K-STABILITY OF FANO MANIFOLDS WITH NOT SMALL ALPHA INVARIANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 30 March 2017, pp. 519-530
- Print publication:
- May 2019
-
- Article
- Export citation
Towards a symplectic version of the Chevalley restriction theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 647-666
- Print publication:
- March 2017
-
- Article
- Export citation
Stable vectors in Moy–Prasad filtrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 09 February 2017, pp. 358-372
- Print publication:
- February 2017
-
- Article
- Export citation
Examples of K-Unstable Fano Manifolds with the Picard Number 1
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 881-891
-
- Article
- Export citation
MODELS OF TORSORS AND THE FUNDAMENTAL GROUP SCHEME
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 05 December 2016, pp. 18-34
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
SUPERORBITS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 20 July 2016, pp. 1065-1120
- Print publication:
- November 2018
-
- Article
- Export citation
TRUNCATED BARSOTTI–TATE GROUPS AND DISPLAYS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 04 April 2016, pp. 541-581
- Print publication:
- June 2018
-
- Article
- Export citation
On the equations and classification of toric quiver varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 265-295
- Print publication:
- April 2016
-
- Article
- Export citation
A State Polytope Decomposition Formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 14 December 2015, pp. 759-776
-
- Article
- Export citation
On Berman–Gibbs stability and K-stability of
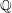 $\mathbb{Q}$-Fano varieties
$\mathbb{Q}$-Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 26 November 2015, pp. 288-298
- Print publication:
- February 2016
-
- Article
- Export citation