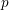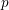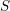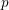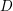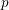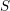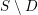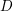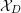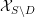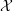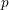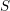1 Introduction
Let
![]() $S$
be a scheme in positive characteristic
$S$
be a scheme in positive characteristic
![]() $p$
. A
$p$
. A
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $S$
is called NP-constant if all of its geometric fibers have the same Newton polygon. In [Reference Zink19], Zink proved that if
$S$
is called NP-constant if all of its geometric fibers have the same Newton polygon. In [Reference Zink19], Zink proved that if
![]() $S$
is regular, then any NP-constant
$S$
is regular, then any NP-constant
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $S$
is isogenous to a
$S$
is isogenous to a
![]() $p$
-divisible group that has a slope filtration. The case that
$p$
-divisible group that has a slope filtration. The case that
![]() $S$
is finitely generated over a perfect field with
$S$
is finitely generated over a perfect field with
![]() $\dim (S)=1$
had already been shown by Katz [Reference Katz7, Corollary 2.6.3]. The result of Oort and Zink [Reference Oort and Zink13, Theorem 2.1] is quite general, where they showed that the same statement holds even when
$\dim (S)=1$
had already been shown by Katz [Reference Katz7, Corollary 2.6.3]. The result of Oort and Zink [Reference Oort and Zink13, Theorem 2.1] is quite general, where they showed that the same statement holds even when
![]() $S$
is a normal Noetherian scheme.
$S$
is a normal Noetherian scheme.
The aim of this paper is to weaken the NP-constancy condition. Since the condition on slope filtration makes sense only for NP-constant
![]() $p$
-divisible groups, we instead use the condition that all geometric fibers are minimal. The definition of minimality of [Reference Oort12, 1.1] is recalled in Definition 3.4. Note that any NP-constant
$p$
-divisible groups, we instead use the condition that all geometric fibers are minimal. The definition of minimality of [Reference Oort12, 1.1] is recalled in Definition 3.4. Note that any NP-constant
![]() $p$
-divisible group whose geometric fibers are all minimal has a slope filtration.
$p$
-divisible group whose geometric fibers are all minimal has a slope filtration.
Let
![]() $S$
be a scheme in characteristic
$S$
be a scheme in characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $D$
be a closed subscheme on
$D$
be a closed subscheme on
![]() $S$
. An NP-saturated
$S$
. An NP-saturated
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $(S,D)$
is a
$(S,D)$
is a
![]() $p$
-divisible group
$p$
-divisible group
![]() ${\mathcal{X}}$
over
${\mathcal{X}}$
over
![]() $S$
such that
$S$
such that
![]() ${\mathcal{X}}_{S\setminus D}$
and
${\mathcal{X}}_{S\setminus D}$
and
![]() ${\mathcal{X}}_{D}$
are NP-constant and the Newton polygon of
${\mathcal{X}}_{D}$
are NP-constant and the Newton polygon of
![]() ${\mathcal{X}}_{D}$
is saturated in that of
${\mathcal{X}}_{D}$
is saturated in that of
![]() ${\mathcal{X}}_{S\setminus D}$
. Here, for two Newton polygons
${\mathcal{X}}_{S\setminus D}$
. Here, for two Newton polygons
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}$
where
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}$
where
![]() $\unicode[STIX]{x1D701}$
is less than
$\unicode[STIX]{x1D701}$
is less than
![]() $\unicode[STIX]{x1D709}$
, we say that
$\unicode[STIX]{x1D709}$
, we say that
![]() $\unicode[STIX]{x1D701}$
is saturated in
$\unicode[STIX]{x1D701}$
is saturated in
![]() $\unicode[STIX]{x1D709}$
if there is no other Newton polygon between
$\unicode[STIX]{x1D709}$
if there is no other Newton polygon between
![]() $\unicode[STIX]{x1D701}$
and
$\unicode[STIX]{x1D701}$
and
![]() $\unicode[STIX]{x1D709}$
. As a corollary of our main theorem (Theorem 4.2), we have the following.
$\unicode[STIX]{x1D709}$
. As a corollary of our main theorem (Theorem 4.2), we have the following.
Corollary 1.1. Assume that
![]() $S$
is Noetherian and normal and that
$S$
is Noetherian and normal and that
![]() $D$
is a prime Weil divisor. Then, any NP-saturated
$D$
is a prime Weil divisor. Then, any NP-saturated
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $(S,D)$
is isogenous to a
$(S,D)$
is isogenous to a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $S$
whose geometric fibers are all minimal.
$S$
whose geometric fibers are all minimal.
This means that in order to classify up to isogeny, NP-saturated
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $(S,D)$
as in Corollary 1.1, it suffices to look into NP-saturated
$(S,D)$
as in Corollary 1.1, it suffices to look into NP-saturated
![]() $p$
-divisible groups whose geometric fibers are all minimal. Such
$p$
-divisible groups whose geometric fibers are all minimal. Such
![]() $p$
-divisible groups are very specific, and can be said to be concrete objects in the deformation theory at least for local
$p$
-divisible groups are very specific, and can be said to be concrete objects in the deformation theory at least for local
![]() $S$
, since the isomorphism class of every geometric fiber is determined.
$S$
, since the isomorphism class of every geometric fiber is determined.
This paper is organized as follows. In Section 2, we introduce the notion of quasi-saturated Newton polygons. The above corollary is regarded as a special case of a more general result on NP-quasi-saturated
![]() $p$
-divisible groups. In Section 3, we investigate the relation between the slope-divisibility and the minimality of
$p$
-divisible groups. In Section 3, we investigate the relation between the slope-divisibility and the minimality of
![]() $p$
-divisible groups. We introduce an isogeny
$p$
-divisible groups. We introduce an isogeny
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
in (18) and show some nice properties of the isogeny, which are used in the next section. The first part of Section 4 is the heart of this paper, where we prove the theorem in the case of
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
in (18) and show some nice properties of the isogeny, which are used in the next section. The first part of Section 4 is the heart of this paper, where we prove the theorem in the case of
![]() $S=\operatorname{Spec}(R)$
with discrete valuation ring
$S=\operatorname{Spec}(R)$
with discrete valuation ring
![]() $R$
. In the second part, we extend it to general
$R$
. In the second part, we extend it to general
![]() $(S,D)$
as in Corollary 1.1, using the ideas invented by [Reference Oort and Zink13]. In Section 5, as an application, we give a geometrical proof of the unpolarized analog of [Reference Harashita2, Corollary 3.2] on the configuration of the minimal
$(S,D)$
as in Corollary 1.1, using the ideas invented by [Reference Oort and Zink13]. In Section 5, as an application, we give a geometrical proof of the unpolarized analog of [Reference Harashita2, Corollary 3.2] on the configuration of the minimal
![]() $p$
-kernel type, and show the unpolarized analog of Oort’s conjecture.
$p$
-kernel type, and show the unpolarized analog of Oort’s conjecture.
2 Quasi-saturated Newton polygons
A Newton polygon is a finite multiset of coprime pairs of nonnegative integers
that is to say, a function from the set of coprime pairs of nonnegative integers to the set of nonnegative integers with finite support. We define the addition of Newton polygons to be the addition of their functions, which are denoted by
![]() $+_{\operatorname{NP}}$
, so that we distinguish this from addition of two-dimensional vectors.
$+_{\operatorname{NP}}$
, so that we distinguish this from addition of two-dimensional vectors.
We regard Newton polygons as upward-convex line graphs defined in the following way. Let
![]() $\unicode[STIX]{x1D709}=\{(m_{1},n_{1}),\ldots ,(m_{t},n_{t})\}$
be a Newton polygon. Put
$\unicode[STIX]{x1D709}=\{(m_{1},n_{1}),\ldots ,(m_{t},n_{t})\}$
be a Newton polygon. Put
![]() $h=\sum _{i=1}^{t}(m_{i}+n_{i})$
and
$h=\sum _{i=1}^{t}(m_{i}+n_{i})$
and
![]() $d=\sum _{i=1}^{t}n_{i}$
. Set
$d=\sum _{i=1}^{t}n_{i}$
. Set
![]() $\unicode[STIX]{x1D706}_{i}=n_{i}/h_{i}$
with
$\unicode[STIX]{x1D706}_{i}=n_{i}/h_{i}$
with
![]() $h_{i}:=m_{i}+n_{i}$
. We arrange the coprime pairs
$h_{i}:=m_{i}+n_{i}$
. We arrange the coprime pairs
![]() $(m_{i},n_{i})$
(
$(m_{i},n_{i})$
(
![]() $i=1,\ldots ,t$
) so that
$i=1,\ldots ,t$
) so that
To
![]() $\unicode[STIX]{x1D709}$
we associate the line graph obtained as the upper convex hull of the points
$\unicode[STIX]{x1D709}$
we associate the line graph obtained as the upper convex hull of the points
![]() $\sum _{i=1}^{j}(h_{i},n_{i})$
for
$\sum _{i=1}^{j}(h_{i},n_{i})$
for
![]() $j=0,\ldots ,t$
. The line graph starts at
$j=0,\ldots ,t$
. The line graph starts at
![]() $(0,0)$
and ends at
$(0,0)$
and ends at
![]() $(h,d)$
. We call
$(h,d)$
. We call
![]() $(h_{i},n_{i})$
(
$(h_{i},n_{i})$
(
![]() $i=1,\ldots ,t$
) segments of
$i=1,\ldots ,t$
) segments of
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
Let
![]() $\unicode[STIX]{x1D709}$
be a Newton polygon. If a point
$\unicode[STIX]{x1D709}$
be a Newton polygon. If a point
![]() $P$
is below or on
$P$
is below or on
![]() $\unicode[STIX]{x1D709}$
, we write
$\unicode[STIX]{x1D709}$
, we write
![]() $P$
$P$
![]() $\preccurlyeq \unicode[STIX]{x1D709}$
. For another Newton polygon
$\preccurlyeq \unicode[STIX]{x1D709}$
. For another Newton polygon
![]() $\unicode[STIX]{x1D701}$
whose end point is equal to that of
$\unicode[STIX]{x1D701}$
whose end point is equal to that of
![]() $\unicode[STIX]{x1D709}$
, we say
$\unicode[STIX]{x1D709}$
, we say
![]() $\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
if for every point
$\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
if for every point
![]() $P$
on
$P$
on
![]() $\unicode[STIX]{x1D701}$
we have
$\unicode[STIX]{x1D701}$
we have
![]() $P\preccurlyeq \unicode[STIX]{x1D709}$
. We say
$P\preccurlyeq \unicode[STIX]{x1D709}$
. We say
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
if
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
if
![]() $\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D701}\neq \unicode[STIX]{x1D709}$
. Let
$\unicode[STIX]{x1D701}\neq \unicode[STIX]{x1D709}$
. Let
![]() $\unicode[STIX]{x1D701}$
and
$\unicode[STIX]{x1D701}$
and
![]() $\unicode[STIX]{x1D709}$
be Newton polygons with
$\unicode[STIX]{x1D709}$
be Newton polygons with
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
. We say that
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
. We say that
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is saturated if there is no Newton polygon
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is saturated if there is no Newton polygon
![]() $\unicode[STIX]{x1D702}$
such that
$\unicode[STIX]{x1D702}$
such that
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D702}\prec \unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D702}\prec \unicode[STIX]{x1D709}$
.
In the rest of this section, we introduce the notion of quasi-saturated pairs of Newton polygons, for which almost all arguments in this paper work, and give a numerical criterion for the saturatedness in the case that
![]() $\unicode[STIX]{x1D709}$
consists of two segments (see Lemma 2.2 below).
$\unicode[STIX]{x1D709}$
consists of two segments (see Lemma 2.2 below).
To a rational number
![]() $\unicode[STIX]{x1D706}=r/s$
with coprime nonnegative integers
$\unicode[STIX]{x1D706}=r/s$
with coprime nonnegative integers
![]() $r,s$
, we associate the two-dimensional vectors
$r,s$
, we associate the two-dimensional vectors
and
for a Newton polygon
![]() $\unicode[STIX]{x1D709}$
of the form (1). We use the alternating form
$\unicode[STIX]{x1D709}$
of the form (1). We use the alternating form
![]() $\langle ~,~\rangle$
on two-dimensional vectors:
$\langle ~,~\rangle$
on two-dimensional vectors:
If
![]() $\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
, then we have
$\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
, then we have
![]() $\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle \geqslant 0$
for any
$\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle \geqslant 0$
for any
![]() $\unicode[STIX]{x1D706}$
. This is clear if we know the following graphical meaning of the value
$\unicode[STIX]{x1D706}$
. This is clear if we know the following graphical meaning of the value
![]() $\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})\rangle$
: for
$\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})\rangle$
: for
![]() $v_{\unicode[STIX]{x1D706}}=(s,r)$
, the line with slope
$v_{\unicode[STIX]{x1D706}}=(s,r)$
, the line with slope
![]() $r/s$
that is tangent to
$r/s$
that is tangent to
![]() $\unicode[STIX]{x1D709}$
is given by
$\unicode[STIX]{x1D709}$
is given by
See Figure 1. Note that
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
is the first point where
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
is the first point where
![]() $\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
is tangent to
$\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
is tangent to
![]() $\unicode[STIX]{x1D709}$
. If
$\unicode[STIX]{x1D709}$
. If
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D701}$
, then
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D701}$
, then
![]() $\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
is below or on
$\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
is below or on
![]() $\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
, whence
$\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
, whence
![]() $\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle \leqslant \langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})\rangle$
.
$\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle \leqslant \langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})\rangle$
.

Figure 1.
![]() $\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
is the line with slope
$\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
is the line with slope
![]() $\unicode[STIX]{x1D706}$
that is tangent to
$\unicode[STIX]{x1D706}$
that is tangent to
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
Definition 2.1. We say that
![]() $\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
is quasi-saturated if for each slope
$\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
is quasi-saturated if for each slope
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $\unicode[STIX]{x1D701}$
, we have
$\unicode[STIX]{x1D701}$
, we have
![]() $\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle \leqslant 1$
.
$\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle \leqslant 1$
.
Note that the condition of
![]() $\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle \leqslant 1$
is equivalent to there being no lattice point properly between
$\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle \leqslant 1$
is equivalent to there being no lattice point properly between
![]() $\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
and
$\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})$
and
![]() $\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
.
$\ell _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
.
Lemma 2.2. If
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is saturated, then
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is saturated, then
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is quasi-saturated. The converse holds if
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is quasi-saturated. The converse holds if
![]() $\unicode[STIX]{x1D709}$
consists of two segments.
$\unicode[STIX]{x1D709}$
consists of two segments.
Proof. Let
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
be a saturated pair of Newton polygons. One can write
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
be a saturated pair of Newton polygons. One can write
so that
![]() $\unicode[STIX]{x1D701}^{\prime }\prec \unicode[STIX]{x1D709}^{\prime }$
is saturated and
$\unicode[STIX]{x1D701}^{\prime }\prec \unicode[STIX]{x1D709}^{\prime }$
is saturated and
![]() $\unicode[STIX]{x1D709}^{\prime }$
consists of only two segments. Write
$\unicode[STIX]{x1D709}^{\prime }$
consists of only two segments. Write
Note that
![]() $\unicode[STIX]{x1D701}^{\prime }$
and
$\unicode[STIX]{x1D701}^{\prime }$
and
![]() $\unicode[STIX]{x1D71A}$
do not share any slope. For each slope
$\unicode[STIX]{x1D71A}$
do not share any slope. For each slope
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $\unicode[STIX]{x1D71A}$
, we have
$\unicode[STIX]{x1D71A}$
, we have
![]() $\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle =0$
.
$\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle =0$
.
Let
![]() $\unicode[STIX]{x1D706}$
be a slope of
$\unicode[STIX]{x1D706}$
be a slope of
![]() $\unicode[STIX]{x1D701}^{\prime }$
. Let
$\unicode[STIX]{x1D701}^{\prime }$
. Let
![]() $j$
be the smallest index with
$j$
be the smallest index with
![]() $\unicode[STIX]{x1D706}=n_{j}/h_{j}$
with
$\unicode[STIX]{x1D706}=n_{j}/h_{j}$
with
![]() $h_{j}=m_{j}+n_{j}$
. Note that
$h_{j}=m_{j}+n_{j}$
. Note that
![]() $v_{\unicode[STIX]{x1D706}}=(h_{j},n_{j})$
. Put
$v_{\unicode[STIX]{x1D706}}=(h_{j},n_{j})$
. Put
![]() $v=(a_{1}+b_{1},b_{1})$
and
$v=(a_{1}+b_{1},b_{1})$
and
![]() $u_{i}=(h_{i},n_{i})$
, which are considered as two-dimensional vectors. We have
$u_{i}=(h_{i},n_{i})$
, which are considered as two-dimensional vectors. We have
The condition
![]() $\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle =1$
is equivalent to the condition that in the triangle with vertices
$\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle =1$
is equivalent to the condition that in the triangle with vertices
![]() $v,\sum _{i<j}u_{i}$
and
$v,\sum _{i<j}u_{i}$
and
![]() $\sum _{i\leqslant j}u_{i}$
, there is no lattice point other than the vertices. (In this case, the same thing holds for the triangle with vertices
$\sum _{i\leqslant j}u_{i}$
, there is no lattice point other than the vertices. (In this case, the same thing holds for the triangle with vertices
![]() $v,\sum _{i<l}u_{j}$
and
$v,\sum _{i<l}u_{j}$
and
![]() $\sum _{i\leqslant l}u_{i}$
for all
$\sum _{i\leqslant l}u_{i}$
for all
![]() $l$
with
$l$
with
![]() $n_{l}/h_{l}=\unicode[STIX]{x1D706}$
.) Hence, the condition that
$n_{l}/h_{l}=\unicode[STIX]{x1D706}$
.) Hence, the condition that
![]() $\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle =1$
for all slopes
$\langle v_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\rangle =1$
for all slopes
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $\unicode[STIX]{x1D701}^{\prime }$
is equivalent to there being no lattice point
$\unicode[STIX]{x1D701}^{\prime }$
is equivalent to there being no lattice point
![]() $P$
above
$P$
above
![]() $\unicode[STIX]{x1D701}^{\prime }$
with
$\unicode[STIX]{x1D701}^{\prime }$
with
![]() $P\preccurlyeq \unicode[STIX]{x1D709}^{\prime }$
except the breaking point of
$P\preccurlyeq \unicode[STIX]{x1D709}^{\prime }$
except the breaking point of
![]() $\unicode[STIX]{x1D709}^{\prime }$
. This is equivalent to
$\unicode[STIX]{x1D709}^{\prime }$
. This is equivalent to
![]() $\unicode[STIX]{x1D701}^{\prime }\prec \unicode[STIX]{x1D709}^{\prime }$
being saturated.◻
$\unicode[STIX]{x1D701}^{\prime }\prec \unicode[STIX]{x1D709}^{\prime }$
being saturated.◻
Example 2.3. Let
![]() $\unicode[STIX]{x1D709}=(0,1)+_{\operatorname{NP}}(1,3)+_{\operatorname{NP}}(3,1)+_{\operatorname{NP}}(1,0)$
, and let
$\unicode[STIX]{x1D709}=(0,1)+_{\operatorname{NP}}(1,3)+_{\operatorname{NP}}(3,1)+_{\operatorname{NP}}(1,0)$
, and let
![]() $\unicode[STIX]{x1D701}=(0,1)+_{\operatorname{NP}}(1,2)+_{\operatorname{NP}}(1,1)+_{\operatorname{NP}}(2,1)+_{\operatorname{NP}}(1,0)$
. Note that
$\unicode[STIX]{x1D701}=(0,1)+_{\operatorname{NP}}(1,2)+_{\operatorname{NP}}(1,1)+_{\operatorname{NP}}(2,1)+_{\operatorname{NP}}(1,0)$
. Note that
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is saturated. In the proof of the lemma above, we use the notation
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is saturated. In the proof of the lemma above, we use the notation
![]() $\unicode[STIX]{x1D709}^{\prime }=(1,3)+_{\operatorname{NP}}(3,1)$
and
$\unicode[STIX]{x1D709}^{\prime }=(1,3)+_{\operatorname{NP}}(3,1)$
and
![]() $\unicode[STIX]{x1D701}^{\prime }=(1,2)+_{\operatorname{NP}}(1,1)+_{\operatorname{NP}}(2,1)$
with
$\unicode[STIX]{x1D701}^{\prime }=(1,2)+_{\operatorname{NP}}(1,1)+_{\operatorname{NP}}(2,1)$
with
![]() $\unicode[STIX]{x1D70C}=(0,1)+_{\operatorname{NP}}(1,0)$
. See Figure 2 for the picture of
$\unicode[STIX]{x1D70C}=(0,1)+_{\operatorname{NP}}(1,0)$
. See Figure 2 for the picture of
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
.

Figure 2. The picture of
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
.
In the second statement in Lemma 2.2, the condition that
![]() $\unicode[STIX]{x1D709}$
consists of two segments is necessary.
$\unicode[STIX]{x1D709}$
consists of two segments is necessary.
Example 2.4. Consider
![]() $\unicode[STIX]{x1D709}=(0,1)+_{\operatorname{NP}}(1,1)+_{\operatorname{NP}}(1,0)$
and
$\unicode[STIX]{x1D709}=(0,1)+_{\operatorname{NP}}(1,1)+_{\operatorname{NP}}(1,0)$
and
![]() $\unicode[STIX]{x1D701}=2(1,1)$
. Then,
$\unicode[STIX]{x1D701}=2(1,1)$
. Then,
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is not saturated, since
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is not saturated, since
![]() $\unicode[STIX]{x1D701}\prec (0,1)+_{\operatorname{NP}}(2,1)\prec \unicode[STIX]{x1D709}$
. However,
$\unicode[STIX]{x1D701}\prec (0,1)+_{\operatorname{NP}}(2,1)\prec \unicode[STIX]{x1D709}$
. However,
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is quasi-saturated.
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is quasi-saturated.
3 Slope-divisibility and minimality
A slope with exponent is a pair
![]() $(\unicode[STIX]{x1D706},e)$
of rational number
$(\unicode[STIX]{x1D706},e)$
of rational number
![]() $\unicode[STIX]{x1D706}$
with
$\unicode[STIX]{x1D706}$
with
![]() $0\leqslant \unicode[STIX]{x1D706}\leqslant 1$
and integer
$0\leqslant \unicode[STIX]{x1D706}\leqslant 1$
and integer
![]() $e\neq 0$
. Let
$e\neq 0$
. Let
![]() $\unicode[STIX]{x1D6EC}$
be the set of slopes with exponents
$\unicode[STIX]{x1D6EC}$
be the set of slopes with exponents
For
![]() $\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)\in \unicode[STIX]{x1D6EC}$
, we call
$\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)\in \unicode[STIX]{x1D6EC}$
, we call
![]() $e$
the exponent of
$e$
the exponent of
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $\unicode[STIX]{x1D706}$
the slope of
$\unicode[STIX]{x1D706}$
the slope of
![]() $\unicode[STIX]{x1D707}$
, which will be denoted by
$\unicode[STIX]{x1D707}$
, which will be denoted by
![]() $\overline{\unicode[STIX]{x1D707}}$
,
$\overline{\unicode[STIX]{x1D707}}$
,
Let
![]() $\unicode[STIX]{x1D6EC}_{e}$
be the subset of
$\unicode[STIX]{x1D6EC}_{e}$
be the subset of
![]() $\unicode[STIX]{x1D6EC}$
consisting of elements with exponent
$\unicode[STIX]{x1D6EC}$
consisting of elements with exponent
![]() $e$
. We identify
$e$
. We identify
![]() $\unicode[STIX]{x1D6EC}_{1}$
with
$\unicode[STIX]{x1D6EC}_{1}$
with
![]() $\{\unicode[STIX]{x1D706}\in \mathbb{Q}\mid 0\leqslant \unicode[STIX]{x1D706}\leqslant 1\}$
, the set of usual slopes, by mapping
$\{\unicode[STIX]{x1D706}\in \mathbb{Q}\mid 0\leqslant \unicode[STIX]{x1D706}\leqslant 1\}$
, the set of usual slopes, by mapping
![]() $(\unicode[STIX]{x1D706},1)$
to
$(\unicode[STIX]{x1D706},1)$
to
![]() $\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}$
. Let
![]() $\unicode[STIX]{x1D6EC}_{+}$
(resp.
$\unicode[STIX]{x1D6EC}_{+}$
(resp.
![]() $\unicode[STIX]{x1D6EC}_{-}$
) be the subset of
$\unicode[STIX]{x1D6EC}_{-}$
) be the subset of
![]() $\unicode[STIX]{x1D6EC}$
consisting of elements with positive (resp. negative) exponents. We use the embedding of
$\unicode[STIX]{x1D6EC}$
consisting of elements with positive (resp. negative) exponents. We use the embedding of
![]() $\unicode[STIX]{x1D6EC}$
into
$\unicode[STIX]{x1D6EC}$
into
![]() $\mathbb{Z}^{2}$
sending
$\mathbb{Z}^{2}$
sending
![]() $\unicode[STIX]{x1D707}=(r/s,e)$
with coprime integers
$\unicode[STIX]{x1D707}=(r/s,e)$
with coprime integers
![]() $r,s\geqslant 0$
to
$r,s\geqslant 0$
to
Let
![]() $S$
be a scheme in characteristic
$S$
be a scheme in characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $\operatorname{Frob}_{S}:S\rightarrow S$
be the Frobenius morphism. Let
$\operatorname{Frob}_{S}:S\rightarrow S$
be the Frobenius morphism. Let
![]() $X$
be a
$X$
be a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $S$
. Set
$S$
. Set
![]() $X^{(p^{a})}=X\times _{\operatorname{Frob}_{S}^{a}}S$
. We denote by
$X^{(p^{a})}=X\times _{\operatorname{Frob}_{S}^{a}}S$
. We denote by
![]() $\operatorname{Fr}:X\rightarrow X^{(p)}$
the relative Frobenius homomorphism and by
$\operatorname{Fr}:X\rightarrow X^{(p)}$
the relative Frobenius homomorphism and by
![]() $\operatorname{Ver}:X^{(p)}\rightarrow X$
the Verschiebung.
$\operatorname{Ver}:X^{(p)}\rightarrow X$
the Verschiebung.
For
![]() $\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)\in \unicode[STIX]{x1D6EC}$
, we write
$\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)\in \unicode[STIX]{x1D6EC}$
, we write
![]() $\unicode[STIX]{x1D706}=r/s$
with coprime integers
$\unicode[STIX]{x1D706}=r/s$
with coprime integers
![]() $r,s\geqslant 0$
, and consider the quasi-isogeny
$r,s\geqslant 0$
, and consider the quasi-isogeny
from
![]() $X$
to
$X$
to
![]() $X^{(p^{se})}$
if
$X^{(p^{se})}$
if
![]() $e>0$
and from
$e>0$
and from
![]() $X^{(p^{se})}$
to
$X^{(p^{se})}$
to
![]() $X$
if
$X$
if
![]() $e<0$
. This is simply referred as “
$e<0$
. This is simply referred as “
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
![]() $X$
”.
$X$
”.
Definition 3.1. Let
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
. We say that
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
. We say that
![]() $X$
is slope divisible (resp. isoclinic and slope divisible) with respect to
$X$
is slope divisible (resp. isoclinic and slope divisible) with respect to
![]() $\unicode[STIX]{x1D707}$
if the quasi-isogeny
$\unicode[STIX]{x1D707}$
if the quasi-isogeny
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
![]() $X$
is an isogeny (resp. isomorphism), where
$X$
is an isogeny (resp. isomorphism), where
![]() $X=0$
is allowed.
$X=0$
is allowed.
Remark 3.2. If
![]() $X$
is slope divisible with respect to
$X$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)$
, then its Serre dual is slope divisible with respect to
$\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)$
, then its Serre dual is slope divisible with respect to
![]() $(1-\unicode[STIX]{x1D706},-e)$
, because the dual of
$(1-\unicode[STIX]{x1D706},-e)$
, because the dual of
![]() $p^{-r}\operatorname{Fr}^{s}$
on
$p^{-r}\operatorname{Fr}^{s}$
on
![]() $X$
is
$X$
is
![]() $p^{-r}\operatorname{Ver}^{s}=\left(p^{-(s-r)}\operatorname{Fr}^{s}\right)^{-1}$
on the Serre dual. In general, when we consider
$p^{-r}\operatorname{Ver}^{s}=\left(p^{-(s-r)}\operatorname{Fr}^{s}\right)^{-1}$
on the Serre dual. In general, when we consider
![]() $\operatorname{Ver}$
-slopes, negative exponents appear naturally.
$\operatorname{Ver}$
-slopes, negative exponents appear naturally.
For
![]() $\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)\in \unicode[STIX]{x1D6EC}$
, we set
$\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)\in \unicode[STIX]{x1D6EC}$
, we set
![]() $\unicode[STIX]{x1D707}^{\ast }:=(\unicode[STIX]{x1D706},-e)$
. Note that
$\unicode[STIX]{x1D707}^{\ast }:=(\unicode[STIX]{x1D706},-e)$
. Note that
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}^{\ast }}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}^{-1}$
.
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}^{\ast }}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}^{-1}$
.
Definition 3.3. Let
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
. Let
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
. Let
![]() $Y\subset X$
be a closed immersion of
$Y\subset X$
be a closed immersion of
![]() $p$
-divisible groups. We say that
$p$
-divisible groups. We say that
![]() $Y$
in
$Y$
in
![]() $X$
is slope bi-divisible with respect to
$X$
is slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}$
if the quasi-isogeny
$\unicode[STIX]{x1D707}$
if the quasi-isogeny
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
![]() $Y$
is an isogeny and also
$Y$
is an isogeny and also
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}^{\ast }}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}^{\ast }}$
on
![]() $X/Y$
is an isogeny.
$X/Y$
is an isogeny.
Let
![]() $\mathbb{D}$
be the covariant Dieudonné functor with
$\mathbb{D}$
be the covariant Dieudonné functor with
![]() $\mathbb{D}(\operatorname{Fr})=V$
and
$\mathbb{D}(\operatorname{Fr})=V$
and
![]() $\mathbb{D}(\operatorname{Ver})=F$
. Let
$\mathbb{D}(\operatorname{Ver})=F$
. Let
![]() $m$
and
$m$
and
![]() $n$
be coprime nonnegative integers. Let
$n$
be coprime nonnegative integers. Let
![]() $H_{m,n}$
be the
$H_{m,n}$
be the
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $\mathbb{F}_{p}$
whose Dieudonné module
$\mathbb{F}_{p}$
whose Dieudonné module
![]() $N_{m,n}=\mathbb{D}(H_{m,n})$
is given by
$N_{m,n}=\mathbb{D}(H_{m,n})$
is given by
with
![]() $F\unicode[STIX]{x1D716}_{i}=\unicode[STIX]{x1D716}_{i+m}$
,
$F\unicode[STIX]{x1D716}_{i}=\unicode[STIX]{x1D716}_{i+m}$
,
![]() $V\unicode[STIX]{x1D716}_{i}=\unicode[STIX]{x1D716}_{i+n}$
and
$V\unicode[STIX]{x1D716}_{i}=\unicode[STIX]{x1D716}_{i+n}$
and
![]() $\unicode[STIX]{x1D716}_{i+m+n}=p\unicode[STIX]{x1D716}_{i}$
. Note that
$\unicode[STIX]{x1D716}_{i+m+n}=p\unicode[STIX]{x1D716}_{i}$
. Note that
![]() $H_{m,n}$
is a simple
$H_{m,n}$
is a simple
![]() $p$
-divisible group with slope
$p$
-divisible group with slope
![]() $n/(m+n)$
. Let
$n/(m+n)$
. Let
![]() $\unicode[STIX]{x1D71B}$
be the endomorphism of
$\unicode[STIX]{x1D71B}$
be the endomorphism of
![]() $H_{m,n}$
characterized by
$H_{m,n}$
characterized by
![]() $\mathbb{D}(\unicode[STIX]{x1D71B})(\unicode[STIX]{x1D716}_{i})=\unicode[STIX]{x1D716}_{i+1}$
. It is straightforward to see that
$\mathbb{D}(\unicode[STIX]{x1D71B})(\unicode[STIX]{x1D716}_{i})=\unicode[STIX]{x1D716}_{i+1}$
. It is straightforward to see that
Let
![]() $K$
be a field of characteristic
$K$
be a field of characteristic
![]() $p$
. A
$p$
. A
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $K$
is called isoclinic and minimal if it is isomorphic over the algebraic closure
$K$
is called isoclinic and minimal if it is isomorphic over the algebraic closure
![]() $\overline{K}$
of
$\overline{K}$
of
![]() $K$
to the product of some copies of
$K$
to the product of some copies of
![]() $\left(H_{m,n}\right)_{\overline{K}}$
for a certain coprime pair
$\left(H_{m,n}\right)_{\overline{K}}$
for a certain coprime pair
![]() $(m,n)$
of nonnegative integers. Clearly, an isoclinic minimal
$(m,n)$
of nonnegative integers. Clearly, an isoclinic minimal
![]() $p$
-divisible group with slope
$p$
-divisible group with slope
![]() $\unicode[STIX]{x1D706}$
is slope divisible with respect to any
$\unicode[STIX]{x1D706}$
is slope divisible with respect to any
![]() $\unicode[STIX]{x1D707}$
with
$\unicode[STIX]{x1D707}$
with
![]() $\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle \geqslant 0$
and is isoclinic and slope divisible with respect to
$\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle \geqslant 0$
and is isoclinic and slope divisible with respect to
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Recall the definition [Reference Oort12, 1.1] of minimal
![]() $p$
-divisible groups. For a Newton polygon
$p$
-divisible groups. For a Newton polygon
![]() $\unicode[STIX]{x1D709}=\{(m_{1},n_{1}),\ldots ,(m_{t},n_{t})\}$
, we set
$\unicode[STIX]{x1D709}=\{(m_{1},n_{1}),\ldots ,(m_{t},n_{t})\}$
, we set
Definition 3.4. A
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $K$
is called minimal if it is isomorphic over
$K$
is called minimal if it is isomorphic over
![]() $\overline{K}$
to
$\overline{K}$
to
![]() $H(\unicode[STIX]{x1D709})_{\overline{K}}$
for some Newton polygon
$H(\unicode[STIX]{x1D709})_{\overline{K}}$
for some Newton polygon
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
Also recall the definition of completely slope divisible
![]() $p$
-divisible groups, which is slightly generalized from that in [Reference Oort and Zink13, 1.2] for later use. Let us introduce a partial variant at the same time.
$p$
-divisible groups, which is slightly generalized from that in [Reference Oort and Zink13, 1.2] for later use. Let us introduce a partial variant at the same time.
Definition 3.5. Let
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }\in \unicode[STIX]{x1D6EC}_{+}$
, with
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }\in \unicode[STIX]{x1D6EC}_{+}$
, with
![]() $\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. A
$\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. A
![]() $p$
-divisible group
$p$
-divisible group
![]() $X$
is called partially completely slope divisible with respect to
$X$
is called partially completely slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
if there exists a filtration by closed immersions of
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
if there exists a filtration by closed immersions of
![]() $p$
-divisible groups
$p$
-divisible groups
such that
(i) the
 $X_{j}$
$X_{j}$
 $(j\leqslant i)$
are slope divisible with respect to
$(j\leqslant i)$
are slope divisible with respect to
 $\unicode[STIX]{x1D707}_{i}$
for
$\unicode[STIX]{x1D707}_{i}$
for
 $1\leqslant i\leqslant \ell$
;
$1\leqslant i\leqslant \ell$
;(ii)
 $\operatorname{Gr}_{i}(X):=X_{i}/X_{i-1}$
is isoclinic and slope divisible with respect to
$\operatorname{Gr}_{i}(X):=X_{i}/X_{i-1}$
is isoclinic and slope divisible with respect to
 $\unicode[STIX]{x1D707}_{i}$
for
$\unicode[STIX]{x1D707}_{i}$
for
 $1\leqslant i\leqslant \ell$
;
$1\leqslant i\leqslant \ell$
;(iii) all of the slopes of
 $X_{0}$
are greater than
$X_{0}$
are greater than
 $\overline{\unicode[STIX]{x1D707}_{1}}$
.
$\overline{\unicode[STIX]{x1D707}_{1}}$
.
When
![]() $X_{0}=0$
, we remove partially.
$X_{0}=0$
, we remove partially.
In the same way as in [Reference Zink19, Corollary 11], one can show the following.
Lemma 3.6. Assume that
![]() $K$
is a perfect field of characteristic
$K$
is a perfect field of characteristic
![]() $p$
. Let
$p$
. Let
![]() $X$
be a partially completely slope divisible
$X$
be a partially completely slope divisible
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $K$
with respect to
$K$
with respect to
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
. Then,
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
. Then,
![]() $X$
is isomorphic to
$X$
is isomorphic to
![]() $X_{0}\oplus \bigoplus _{i=1}^{\ell }\operatorname{Gr}_{i}(X)$
.
$X_{0}\oplus \bigoplus _{i=1}^{\ell }\operatorname{Gr}_{i}(X)$
.
Let us define the bi-divisible variant.
Definition 3.7. Let
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }\in \unicode[STIX]{x1D6EC}_{+}$
, with
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }\in \unicode[STIX]{x1D6EC}_{+}$
, with
![]() $\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. A
$\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. A
![]() $p$
-divisible group
$p$
-divisible group
![]() $X$
is called partially completely slope bi-divisible with respect to
$X$
is called partially completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
if there exists a filtration by closed immersions of
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
if there exists a filtration by closed immersions of
![]() $p$
-divisible groups
$p$
-divisible groups
such that
(i) the
 $X_{j}$
$X_{j}$
 $(j\leqslant i)$
are slope divisible with respect to
$(j\leqslant i)$
are slope divisible with respect to
 $\unicode[STIX]{x1D707}_{i}$
for
$\unicode[STIX]{x1D707}_{i}$
for
 $1\leqslant i\leqslant \ell$
;
$1\leqslant i\leqslant \ell$
;(ii) the
 $X/X_{j}$
$X/X_{j}$
 $(j\geqslant i-1)$
are slope divisible with respect to
$(j\geqslant i-1)$
are slope divisible with respect to
 $\unicode[STIX]{x1D707}_{i}^{\ast }$
for
$\unicode[STIX]{x1D707}_{i}^{\ast }$
for
 $1\leqslant i\leqslant \ell$
;
$1\leqslant i\leqslant \ell$
;(iii) all of the slopes of
 $X_{0}$
are greater than
$X_{0}$
are greater than
 $\overline{\unicode[STIX]{x1D707}_{1}}$
.
$\overline{\unicode[STIX]{x1D707}_{1}}$
.
When
![]() $X_{0}=0$
, we remove partially.
$X_{0}=0$
, we remove partially.
Lemma 3.8. Let
![]() $X$
be a
$X$
be a
![]() $p$
-divisible group. Assume that
$p$
-divisible group. Assume that
![]() $X$
is partially completely slope bi-divisible with respect to
$X$
is partially completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
. Then, we have the following.
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
. Then, we have the following.
(1)
 $X$
is partially completely slope divisible with respect to
$X$
is partially completely slope divisible with respect to
 $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.(2) For
 $i=1,\ldots ,\ell$
, we have that
$i=1,\ldots ,\ell$
, we have that
 $\operatorname{Gr}_{i}(X)$
is slope divisible with respect to
$\operatorname{Gr}_{i}(X)$
is slope divisible with respect to
 $\unicode[STIX]{x1D707}_{a}$
for
$\unicode[STIX]{x1D707}_{a}$
for
 $a\geqslant i$
and
$a\geqslant i$
and
 $\unicode[STIX]{x1D707}_{b}^{\ast }$
for
$\unicode[STIX]{x1D707}_{b}^{\ast }$
for
 $b\leqslant i$
.
$b\leqslant i$
.
Proof. (1) The quasi-isogeny
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}:X_{i}/X_{i-1}\rightarrow X_{i}/X_{i-1}$
is an isogeny, because this is induced by the isogeny
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}:X_{i}/X_{i-1}\rightarrow X_{i}/X_{i-1}$
is an isogeny, because this is induced by the isogeny
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}$
on
![]() $X_{i}$
. Consider the composition
$X_{i}$
. Consider the composition
![]() $X_{i}/X_{i-1}\rightarrow X_{i}/X_{i-1}\rightarrow X/X_{i-1}$
of
$X_{i}/X_{i-1}\rightarrow X_{i}/X_{i-1}\rightarrow X/X_{i-1}$
of
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}$
and the restriction to
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}$
and the restriction to
![]() $X_{i}/X_{i-1}$
of
$X_{i}/X_{i-1}$
of
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}^{\ast }}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}^{\ast }}$
on
![]() $X/X_{i-1}$
. Since
$X/X_{i-1}$
. Since
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}^{\ast }}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}^{-1}$
, this composition is identical on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}^{\ast }}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}^{-1}$
, this composition is identical on
![]() $X_{i}/X_{i-1}$
. In particular, the kernel of
$X_{i}/X_{i-1}$
. In particular, the kernel of
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}:X_{i}/X_{i-1}\rightarrow X_{i}/X_{i-1}$
is zero. Hence,
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{i}}:X_{i}/X_{i-1}\rightarrow X_{i}/X_{i-1}$
is zero. Hence,
![]() $X_{i}/X_{i-1}$
is isoclinic and slope divisible with respect to
$X_{i}/X_{i-1}$
is isoclinic and slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{i}$
.
$\unicode[STIX]{x1D707}_{i}$
.
(2) It suffices to show this for each geometric fiber. Hence, we may assume that
![]() $X$
is a
$X$
is a
![]() $p$
-divisible group over an algebraically closed field. By Lemma 3.6,
$p$
-divisible group over an algebraically closed field. By Lemma 3.6,
![]() $X$
is isomorphic to
$X$
is isomorphic to
![]() $X_{0}\oplus \bigoplus _{i=1}^{\ell }\operatorname{Gr}_{i}(X)$
. Since
$X_{0}\oplus \bigoplus _{i=1}^{\ell }\operatorname{Gr}_{i}(X)$
. Since
![]() $X_{i}$
is slope divisible with respect to
$X_{i}$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{a}$
for
$\unicode[STIX]{x1D707}_{a}$
for
![]() $a\geqslant i$
, its direct summand
$a\geqslant i$
, its direct summand
![]() $\operatorname{Gr}_{i}(X)$
is also slope divisible with respect to
$\operatorname{Gr}_{i}(X)$
is also slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{a}$
for
$\unicode[STIX]{x1D707}_{a}$
for
![]() $a\geqslant i$
. Since
$a\geqslant i$
. Since
![]() $X/X_{i-1}$
is slope divisible with respect to
$X/X_{i-1}$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{b}^{\ast }$
for
$\unicode[STIX]{x1D707}_{b}^{\ast }$
for
![]() $b\leqslant i$
, its direct summand
$b\leqslant i$
, its direct summand
![]() $\operatorname{Gr}_{i}(X)$
is also slope divisible with respect to
$\operatorname{Gr}_{i}(X)$
is also slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{b}^{\ast }$
for
$\unicode[STIX]{x1D707}_{b}^{\ast }$
for
![]() $b\leqslant i$
.◻
$b\leqslant i$
.◻
Remark 3.9. Let
![]() $X$
be a minimal
$X$
be a minimal
![]() $p$
-divisible group over a field
$p$
-divisible group over a field
![]() $K$
of characteristic
$K$
of characteristic
![]() $p$
. Then,
$p$
. Then,
![]() $X$
is completely slope bi-divisible with respect to its slopes.
$X$
is completely slope bi-divisible with respect to its slopes.
Example 3.10. Let
![]() $N_{3,2}=\bigoplus _{i=1}^{5}\mathbb{Z}_{p}\unicode[STIX]{x1D716}_{i}$
be as in (10). Let
$N_{3,2}=\bigoplus _{i=1}^{5}\mathbb{Z}_{p}\unicode[STIX]{x1D716}_{i}$
be as in (10). Let
![]() $M$
be the Dieudonné submodule of
$M$
be the Dieudonné submodule of
![]() $N_{3,2}$
generated by
$N_{3,2}$
generated by
![]() $\unicode[STIX]{x1D716}_{1},p\unicode[STIX]{x1D716}_{2},\unicode[STIX]{x1D716}_{3},\unicode[STIX]{x1D716}_{4},\unicode[STIX]{x1D716}_{5}$
. Let
$\unicode[STIX]{x1D716}_{1},p\unicode[STIX]{x1D716}_{2},\unicode[STIX]{x1D716}_{3},\unicode[STIX]{x1D716}_{4},\unicode[STIX]{x1D716}_{5}$
. Let
![]() $Y$
be a
$Y$
be a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $\mathbb{F}_{p}$
whose Dieudonné module is isomorphic to
$\mathbb{F}_{p}$
whose Dieudonné module is isomorphic to
![]() $M$
. Let
$M$
. Let
![]() $X=H_{1,1}\oplus Y$
. Set
$X=H_{1,1}\oplus Y$
. Set
![]() $\unicode[STIX]{x1D707}_{1}=(1/2,1)$
and
$\unicode[STIX]{x1D707}_{1}=(1/2,1)$
and
![]() $\unicode[STIX]{x1D707}_{2}=(2/5,1)$
. Note that
$\unicode[STIX]{x1D707}_{2}=(2/5,1)$
. Note that
![]() $X$
is completely slope divisible with respect to
$X$
is completely slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$
, whose slope filtration is
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$
, whose slope filtration is
![]() $0\subset H_{1,1}\subset X$
. However,
$0\subset H_{1,1}\subset X$
. However,
![]() $X$
is not completely slope bi-divisible with respect to
$X$
is not completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$
, since
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$
, since
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}^{\ast }}=p^{-1}\operatorname{Ver}^{2}$
is not isogeny on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}^{\ast }}=p^{-1}\operatorname{Ver}^{2}$
is not isogeny on
![]() $Y$
.
$Y$
.
Lemma 3.11. Let
![]() ${\mathcal{X}}$
be an NP-constant
${\mathcal{X}}$
be an NP-constant
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $S$
. Then, the subset of points of
$S$
. Then, the subset of points of
![]() $S$
over which the fiber of
$S$
over which the fiber of
![]() ${\mathcal{X}}$
is completely slope bi-divisible with respect to
${\mathcal{X}}$
is completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
is closed in
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
is closed in
![]() $S$
.
$S$
.
Proof. Write
![]() $v_{\unicode[STIX]{x1D707}_{i}}=(s_{i},r_{i})$
. Let
$v_{\unicode[STIX]{x1D707}_{i}}=(s_{i},r_{i})$
. Let
![]() $s$
be the least common multiple of
$s$
be the least common multiple of
![]() $s_{1},\ldots ,s_{\ell }$
. Let
$s_{1},\ldots ,s_{\ell }$
. Let
![]() $\unicode[STIX]{x1D707}_{i}^{\prime }$
be the elements of
$\unicode[STIX]{x1D707}_{i}^{\prime }$
be the elements of
![]() $\unicode[STIX]{x1D6EC}_{+}$
such that
$\unicode[STIX]{x1D6EC}_{+}$
such that
![]() $v_{\unicode[STIX]{x1D707}_{i}^{\prime }}=(s/s_{i})v_{\unicode[STIX]{x1D707}_{i}}$
. By [Reference Oort and Zink13, 2.3], the subset of points of
$v_{\unicode[STIX]{x1D707}_{i}^{\prime }}=(s/s_{i})v_{\unicode[STIX]{x1D707}_{i}}$
. By [Reference Oort and Zink13, 2.3], the subset of points of
![]() $S$
over which the fiber of
$S$
over which the fiber of
![]() ${\mathcal{X}}$
is completely slope divisible with respect to
${\mathcal{X}}$
is completely slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D707}_{\ell }^{\prime }$
is closed in
$\unicode[STIX]{x1D707}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D707}_{\ell }^{\prime }$
is closed in
![]() $S$
. Then, the lemma follows from the fact [Reference Rapoport and Zink15, Proposition 2.9] that for a quasi-isogeny
$S$
. Then, the lemma follows from the fact [Reference Rapoport and Zink15, Proposition 2.9] that for a quasi-isogeny
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y$
of
$\unicode[STIX]{x1D70C}:X\rightarrow Y$
of
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $S$
, the subset of points of
$S$
, the subset of points of
![]() $S$
over which
$S$
over which
![]() $\unicode[STIX]{x1D70C}$
is an isogeny is closed in
$\unicode[STIX]{x1D70C}$
is an isogeny is closed in
![]() $S$
.◻
$S$
.◻
We see from Remark 3.9 that any minimal
![]() $p$
-divisible group is completely slope divisible. Let us study when a completely slope divisible
$p$
-divisible group is completely slope divisible. Let us study when a completely slope divisible
![]() $p$
-divisible group is minimal.
$p$
-divisible group is minimal.
Proposition 3.12. Let
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{1}$
. Let
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{1}$
. Let
![]() $X$
be a
$X$
be a
![]() $p$
-divisible group over a field
$p$
-divisible group over a field
![]() $K$
of characteristic
$K$
of characteristic
![]() $p$
that is isoclinic and slope divisible with respect to
$p$
that is isoclinic and slope divisible with respect to
![]() $\unicode[STIX]{x1D706}$
. The following are equivalent.
$\unicode[STIX]{x1D706}$
. The following are equivalent.
(1)
 $X$
is minimal.
$X$
is minimal.(2) For any
 $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
with
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
with
 $\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle >0$
, the quasi-isogeny
$\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle >0$
, the quasi-isogeny
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
 $X$
is an isogeny.
$X$
is an isogeny.(3) For a
 $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
with
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
with
 $\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle =1$
, the quasi-isogeny
$\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle =1$
, the quasi-isogeny
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
 $X$
is an isogeny.
$X$
is an isogeny.
Proof. It suffices to show the case that
![]() $K$
is algebraically closed. For
$K$
is algebraically closed. For
![]() $v_{\unicode[STIX]{x1D706}}=(m+n,n)$
, we write
$v_{\unicode[STIX]{x1D706}}=(m+n,n)$
, we write
(1)
![]() $\Rightarrow$
(2): Let
$\Rightarrow$
(2): Let
![]() $X$
be an isoclinic and minimal
$X$
be an isoclinic and minimal
![]() $p$
-divisible group, say
$p$
-divisible group, say
Let
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
with
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
with
![]() $\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle >0$
. As seen in (11),
$\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle >0$
. As seen in (11),
![]() $\mathbb{D}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}})$
on
$\mathbb{D}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}})$
on
![]() $\mathbb{D}(H_{\unicode[STIX]{x1D706}})$
is the map sending
$\mathbb{D}(H_{\unicode[STIX]{x1D706}})$
is the map sending
![]() $\unicode[STIX]{x1D716}_{i}$
to
$\unicode[STIX]{x1D716}_{i}$
to
![]() $\unicode[STIX]{x1D716}_{i+\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle }$
. Thus,
$\unicode[STIX]{x1D716}_{i+\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle }$
. Thus,
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
![]() $H_{\unicode[STIX]{x1D706}}^{\oplus \unicode[STIX]{x1D708}}$
is an isogeny.
$H_{\unicode[STIX]{x1D706}}^{\oplus \unicode[STIX]{x1D708}}$
is an isogeny.
(2)
![]() $\Rightarrow$
(3) is obvious.
$\Rightarrow$
(3) is obvious.
(3)
![]() $\Rightarrow$
(1): Write
$\Rightarrow$
(1): Write
![]() $v_{\unicode[STIX]{x1D706}}=(m+n,n)$
and
$v_{\unicode[STIX]{x1D706}}=(m+n,n)$
and
![]() $v_{\unicode[STIX]{x1D707}}=(a+b,b)$
. Since
$v_{\unicode[STIX]{x1D707}}=(a+b,b)$
. Since
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}=p^{-n}\operatorname{Fr}^{m+n}$
and
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}=p^{-n}\operatorname{Fr}^{m+n}$
and
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}=p^{-b}\operatorname{Fr}^{a+b}$
, we have
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}=p^{-b}\operatorname{Fr}^{a+b}$
, we have
Let
![]() $G_{i}=X[\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}^{i}]$
be the kernel of the isogeny
$G_{i}=X[\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}^{i}]$
be the kernel of the isogeny
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}^{i}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}^{i}$
on
![]() $X$
for
$X$
for
![]() $i=0,1,\ldots ,m+n$
. We have a filtration of
$i=0,1,\ldots ,m+n$
. We have a filtration of
![]() $X[p]$
:
$X[p]$
:
By (16), we have
![]() $\operatorname{Fr}\,G_{i}=G_{i-n}$
and
$\operatorname{Fr}\,G_{i}=G_{i-n}$
and
![]() $\operatorname{Ver}\,G_{i}=G_{i-m}$
. Since
$\operatorname{Ver}\,G_{i}=G_{i-m}$
. Since
![]() $m$
and
$m$
and
![]() $n$
are coprime,
$n$
are coprime,
![]() $\{G_{i}/G_{i-1}\mid i=1,\ldots ,m+n\}$
consists of one
$\{G_{i}/G_{i-1}\mid i=1,\ldots ,m+n\}$
consists of one
![]() $(\operatorname{Ver},\operatorname{Fr}^{-1})$
-cycle (cf. [Reference Kraft8]), whence
$(\operatorname{Ver},\operatorname{Fr}^{-1})$
-cycle (cf. [Reference Kraft8]), whence
![]() $G_{i}/G_{i-1}$
(
$G_{i}/G_{i-1}$
(
![]() $i=1,\ldots ,m+n$
) have the same rank, say
$i=1,\ldots ,m+n$
) have the same rank, say
![]() $\unicode[STIX]{x1D708}$
. Thus,
$\unicode[STIX]{x1D708}$
. Thus,
![]() $X[p]$
is isomorphic to
$X[p]$
is isomorphic to
![]() $(H_{m,n}^{\oplus \unicode[STIX]{x1D708}}[p])_{K}$
, and therefore
$(H_{m,n}^{\oplus \unicode[STIX]{x1D708}}[p])_{K}$
, and therefore
![]() $X$
is minimal by [Reference Oort12].◻
$X$
is minimal by [Reference Oort12].◻
Let us give an alternative proof of a special case of [Reference Oort11, 2.2].
Corollary 3.13. Let
![]() ${\mathcal{X}}$
be an NP-constant
${\mathcal{X}}$
be an NP-constant
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $S$
. Then, the subset of points of
$S$
. Then, the subset of points of
![]() $S$
over which the fiber of
$S$
over which the fiber of
![]() ${\mathcal{X}}$
is minimal is closed in
${\mathcal{X}}$
is minimal is closed in
![]() $S$
.
$S$
.
Proof. Let
![]() $\unicode[STIX]{x1D706}_{1}>\cdots >\unicode[STIX]{x1D706}_{\ell }$
be the slopes of
$\unicode[STIX]{x1D706}_{1}>\cdots >\unicode[STIX]{x1D706}_{\ell }$
be the slopes of
![]() ${\mathcal{X}}$
. In a similar way to that in Lemma 3.11, the subset of points of
${\mathcal{X}}$
. In a similar way to that in Lemma 3.11, the subset of points of
![]() $S$
over which the fiber of
$S$
over which the fiber of
![]() ${\mathcal{X}}$
is completely slope divisible with respect to
${\mathcal{X}}$
is completely slope divisible with respect to
![]() $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
is closed in
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
is closed in
![]() $S$
. Hence, we may assume that
$S$
. Hence, we may assume that
![]() ${\mathcal{X}}$
is completely slope divisible with respect to
${\mathcal{X}}$
is completely slope divisible with respect to
![]() $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
. Let
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
. Let
![]() $0={\mathcal{X}}_{0}\subset {\mathcal{X}}_{1}\subset \cdots \subset {\mathcal{X}}_{\ell }={\mathcal{X}}$
be the slope filtration. Let
$0={\mathcal{X}}_{0}\subset {\mathcal{X}}_{1}\subset \cdots \subset {\mathcal{X}}_{\ell }={\mathcal{X}}$
be the slope filtration. Let
![]() $s$
be a point of
$s$
be a point of
![]() $S$
. Note that
$S$
. Note that
![]() ${\mathcal{X}}_{s}$
is minimal if and only if
${\mathcal{X}}_{s}$
is minimal if and only if
![]() $({\mathcal{X}}_{i}/{\mathcal{X}}_{i-1})_{s}$
is minimal for all
$({\mathcal{X}}_{i}/{\mathcal{X}}_{i-1})_{s}$
is minimal for all
![]() $i=1,\ldots ,\ell$
(cf. Lemma 3.6). By Proposition 3.12,
$i=1,\ldots ,\ell$
(cf. Lemma 3.6). By Proposition 3.12,
![]() $({\mathcal{X}}_{i}/{\mathcal{X}}_{i-1})_{s}$
is minimal if and only if
$({\mathcal{X}}_{i}/{\mathcal{X}}_{i-1})_{s}$
is minimal if and only if
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
![]() $({\mathcal{X}}_{i}/{\mathcal{X}}_{i-1})_{s}$
is an isogeny for some
$({\mathcal{X}}_{i}/{\mathcal{X}}_{i-1})_{s}$
is an isogeny for some
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
with
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
with
![]() $\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle =1$
. Hence, the corollary follows from [Reference Rapoport and Zink15, Proposition 2.9].◻
$\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle =1$
. Hence, the corollary follows from [Reference Rapoport and Zink15, Proposition 2.9].◻
Let
![]() $K$
be a field of characteristic
$K$
be a field of characteristic
![]() $p$
. Recall the definition of the small image of a homomorphism of
$p$
. Recall the definition of the small image of a homomorphism of
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $K$
. This notion was introduced by Zink in [Reference Zink19, Section 3]. Let
$K$
. This notion was introduced by Zink in [Reference Zink19, Section 3]. Let
![]() $g:G\rightarrow H$
be a homomorphism of
$g:G\rightarrow H$
be a homomorphism of
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $K$
. It is shown in [Reference Zink19, Proposition 8] that
$K$
. It is shown in [Reference Zink19, Proposition 8] that
![]() $g$
has a unique factorization in the category of
$g$
has a unique factorization in the category of
![]() $p$
-divisible groups
$p$
-divisible groups
where
![]() $G^{\prime }\rightarrow H^{\prime }$
is an isogeny,
$G^{\prime }\rightarrow H^{\prime }$
is an isogeny,
![]() $H^{\prime }\rightarrow H$
is a monomorphism of
$H^{\prime }\rightarrow H$
is a monomorphism of
![]() $p$
-divisible groups and
$p$
-divisible groups and
![]() $G\rightarrow G^{\prime }$
is a homomorphism satisfying that
$G\rightarrow G^{\prime }$
is a homomorphism satisfying that
![]() $G[p^{n}]\rightarrow G^{\prime }[p^{n}]$
is an epimorphism for each natural number
$G[p^{n}]\rightarrow G^{\prime }[p^{n}]$
is an epimorphism for each natural number
![]() $n$
. We call
$n$
. We call
![]() $G^{\prime }$
the small image of
$G^{\prime }$
the small image of
![]() $g$
. In the proof of [Reference Zink19, Proposition 8], the small image
$g$
. In the proof of [Reference Zink19, Proposition 8], the small image
![]() $G^{\prime }$
is given by the quotient of
$G^{\prime }$
is given by the quotient of
![]() $G$
by
$G$
by
![]() $A^{\prime }$
, where
$A^{\prime }$
, where
![]() $A^{\prime }$
is the unique
$A^{\prime }$
is the unique
![]() $p$
-divisible subgroup of
$p$
-divisible subgroup of
![]() $\operatorname{Ker}(g)$
such that
$\operatorname{Ker}(g)$
such that
![]() $\operatorname{Ker}(g)/A^{\prime }$
is a finite group scheme. If
$\operatorname{Ker}(g)/A^{\prime }$
is a finite group scheme. If
![]() $K$
is perfect, then
$K$
is perfect, then
![]() $\mathbb{D}(G^{\prime })$
is the image of
$\mathbb{D}(G^{\prime })$
is the image of
![]() $\mathbb{D}(g)$
, and
$\mathbb{D}(g)$
, and
![]() $\mathbb{D}(H^{\prime })$
is the smallest direct summand of
$\mathbb{D}(H^{\prime })$
is the smallest direct summand of
![]() $\mathbb{D}(H)$
containing
$\mathbb{D}(H)$
containing
![]() $\mathbb{D}(G^{\prime })$
.
$\mathbb{D}(G^{\prime })$
.
Let
![]() $X$
be a
$X$
be a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $K$
. Let
$K$
. Let
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
, and write
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
, and write
![]() $v_{\unicode[STIX]{x1D707}}=(s,r)$
. Let
$v_{\unicode[STIX]{x1D707}}=(s,r)$
. Let
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
be the small image of
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
be the small image of
where the second morphism is the addition of
![]() $X$
. Let
$X$
. Let
![]() $A=\operatorname{Ker}(f_{\unicode[STIX]{x1D707}})$
. Consider the homomorphism
$A=\operatorname{Ker}(f_{\unicode[STIX]{x1D707}})$
. Consider the homomorphism
![]() $g:X^{(p^{s})}\rightarrow A$
sending
$g:X^{(p^{s})}\rightarrow A$
sending
![]() $y$
to
$y$
to
![]() $(\operatorname{Ver}^{s}y,-p^{s-r}y)$
. The kernel and the cokernel of
$(\operatorname{Ver}^{s}y,-p^{s-r}y)$
. The kernel and the cokernel of
![]() $g$
are finite, since both are killed by
$g$
are finite, since both are killed by
![]() $p^{s-r}$
. Hence, the image
$p^{s-r}$
. Hence, the image
![]() $Z$
of
$Z$
of
![]() $g$
is the maximal
$g$
is the maximal
![]() $p$
-divisible subgroup of
$p$
-divisible subgroup of
![]() $A$
. By the construction of the small image explained above, we have
$A$
. By the construction of the small image explained above, we have
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)=X\times X^{(p^{s})}/Z$
. Composing
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)=X\times X^{(p^{s})}/Z$
. Composing
![]() $(\operatorname{id},0):X\rightarrow X\times X^{(p^{s})}$
and
$(\operatorname{id},0):X\rightarrow X\times X^{(p^{s})}$
and
![]() $X\times X^{(p^{s})}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
, we have an isogeny
$X\times X^{(p^{s})}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
, we have an isogeny
Since the kernel of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
is the intersection of
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
is the intersection of
![]() $Z$
and
$Z$
and
![]() $X\times \{0\}$
, we have the following.
$X\times \{0\}$
, we have the following.
Lemma 3.14. We have
Here, the right-hand side is the image as the fppf sheaf, which is represented by a group scheme
![]() $X^{(p^{s})}[p^{s-r}]/\operatorname{Ker}(\operatorname{Ver}_{X^{(p^{s})}[p^{s-r}]}^{s})$
.
$X^{(p^{s})}[p^{s-r}]/\operatorname{Ker}(\operatorname{Ver}_{X^{(p^{s})}[p^{s-r}]}^{s})$
.
Remark 3.15. Assume that
![]() $K$
is a perfect field. Let
$K$
is a perfect field. Let
![]() $M$
be the Dieudonné module of
$M$
be the Dieudonné module of
![]() $X$
. Then, the Dieudonné module of
$X$
. Then, the Dieudonné module of
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
is
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
is
which is isomorphic to
![]() $p^{-r}V^{s}M+M$
. The isogeny
$p^{-r}V^{s}M+M$
. The isogeny
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
in (18) corresponds to the isogeny
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
in (18) corresponds to the isogeny
![]() $M\rightarrow p^{s-r}M+F^{s}M$
sending
$M\rightarrow p^{s-r}M+F^{s}M$
sending
![]() $m$
to
$m$
to
![]() $p^{s-r}m$
. The Dieudonné module of
$p^{s-r}m$
. The Dieudonné module of
![]() $\operatorname{Ker}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}})$
is
$\operatorname{Ker}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}})$
is
which is isomorphic to
![]() $(M+p^{-(s-r)}F^{s}M)/M$
.
$(M+p^{-(s-r)}F^{s}M)/M$
.
Lemma 3.16. Let
![]() $\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)\in \unicode[STIX]{x1D6EC}_{+}$
. The following are equivalent.
$\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D706},e)\in \unicode[STIX]{x1D6EC}_{+}$
. The following are equivalent.
(1)
 $\log _{p}\deg (\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}})=0$
.
$\log _{p}\deg (\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}})=0$
.(2)
 $X$
is slope divisible with respect to
$X$
is slope divisible with respect to
 $\unicode[STIX]{x1D707}^{\ast }=(\unicode[STIX]{x1D706},-e)$
.
$\unicode[STIX]{x1D707}^{\ast }=(\unicode[STIX]{x1D706},-e)$
.
In this case, in particular, the slopes of
![]() $X$
are less than or equal to
$X$
are less than or equal to
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Proof. From the above remark, it is clear that (1) is equivalent to
![]() $p^{-(s-r)}\operatorname{Ver}^{s}$
is an isogeny on
$p^{-(s-r)}\operatorname{Ver}^{s}$
is an isogeny on
![]() $X$
. Since
$X$
. Since
![]() $p^{-(s-r)}\operatorname{Ver}^{s}=(p^{-r}\operatorname{Fr}^{s})^{-1}$
, we have the lemma.◻
$p^{-(s-r)}\operatorname{Ver}^{s}=(p^{-r}\operatorname{Fr}^{s})^{-1}$
, we have the lemma.◻
For
![]() $\unicode[STIX]{x1D707}=(\overline{\unicode[STIX]{x1D707}},e)\in \unicode[STIX]{x1D6EC}_{+}$
, we set
$\unicode[STIX]{x1D707}=(\overline{\unicode[STIX]{x1D707}},e)\in \unicode[STIX]{x1D6EC}_{+}$
, we set
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D709})$
to be
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D709})$
to be
![]() $\unicode[STIX]{x1D6FC}_{\overline{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D709})$
.
$\unicode[STIX]{x1D6FC}_{\overline{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D709})$
.
Proposition 3.17. Let
![]() $\unicode[STIX]{x1D709}$
be the Newton polygon of
$\unicode[STIX]{x1D709}$
be the Newton polygon of
![]() $X$
. Assume that there is a short exact sequence
$X$
. Assume that there is a short exact sequence
of
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $K$
, which splits over
$K$
, which splits over
![]() $\overline{K}$
. Let
$\overline{K}$
. Let
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
such that the slopes of
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
such that the slopes of
![]() $Y$
are greater than or equal to
$Y$
are greater than or equal to
![]() $\overline{\unicode[STIX]{x1D707}}$
and the slopes of
$\overline{\unicode[STIX]{x1D707}}$
and the slopes of
![]() $Z$
are less than or equal to
$Z$
are less than or equal to
![]() $\overline{\unicode[STIX]{x1D707}}$
. Then, we have
$\overline{\unicode[STIX]{x1D707}}$
. Then, we have
where the equality holds if and only if
![]() $Y$
in
$Y$
in
![]() $X$
is slope bi-divisible with respect to
$X$
is slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}$
.
$\unicode[STIX]{x1D707}$
.
Proof. We may assume that
![]() $K$
is an algebraically closed field and
$K$
is an algebraically closed field and
![]() $X=Y\times Z$
. Let
$X=Y\times Z$
. Let
![]() $h$
(resp.
$h$
(resp.
![]() $d$
) be the height (resp. the dimension) of
$d$
) be the height (resp. the dimension) of
![]() $Y$
. Then,
$Y$
. Then,
![]() $\langle v_{\unicode[STIX]{x1D707}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D709})\rangle =\langle v_{\unicode[STIX]{x1D707}},(h,d)\rangle$
. Let
$\langle v_{\unicode[STIX]{x1D707}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D709})\rangle =\langle v_{\unicode[STIX]{x1D707}},(h,d)\rangle$
. Let
![]() $M$
be the Dieudonné module of
$M$
be the Dieudonné module of
![]() $Y$
. Set
$Y$
. Set
![]() $A=F^{s}M$
and
$A=F^{s}M$
and
![]() $B=p^{s-r}M$
. Then,
$B=p^{s-r}M$
. Then,
Lemma 3.16 says that
![]() $\log _{p}\deg (\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}\text{ on }Z)=0$
if and only if
$\log _{p}\deg (\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}\text{ on }Z)=0$
if and only if
![]() $Z$
is slope divisible with respect to
$Z$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}^{\ast }$
. Since
$\unicode[STIX]{x1D707}^{\ast }$
. Since
![]() $\operatorname{Coker}((A+B)/A\rightarrow M/A)=\operatorname{Coker}((A+B)/B\rightarrow M/B)$
, we have
$\operatorname{Coker}((A+B)/A\rightarrow M/A)=\operatorname{Coker}((A+B)/B\rightarrow M/B)$
, we have
 $$\begin{eqnarray}\displaystyle \operatorname{length}(A+B)/B & = & \displaystyle \operatorname{length}M/B-\operatorname{length}M/A+\operatorname{length}(A+B)/A\nonumber\\ \displaystyle & = & \displaystyle (s-r)h-s(h-d)+\operatorname{length}(A+B)/A\nonumber\\ \displaystyle & = & \displaystyle \langle v_{\unicode[STIX]{x1D707}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D709})\rangle +\operatorname{length}(A+B)/A.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{length}(A+B)/B & = & \displaystyle \operatorname{length}M/B-\operatorname{length}M/A+\operatorname{length}(A+B)/A\nonumber\\ \displaystyle & = & \displaystyle (s-r)h-s(h-d)+\operatorname{length}(A+B)/A\nonumber\\ \displaystyle & = & \displaystyle \langle v_{\unicode[STIX]{x1D707}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D709})\rangle +\operatorname{length}(A+B)/A.\nonumber\end{eqnarray}$$
Obviously,
![]() $(A+B)/A\simeq (M+p^{-r}V^{s}M)/M$
is zero if and only if
$(A+B)/A\simeq (M+p^{-r}V^{s}M)/M$
is zero if and only if
![]() $Y$
is slope divisible with respect to
$Y$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}$
.◻
$\unicode[STIX]{x1D707}$
.◻
Lemma 3.18. Let
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
, and let
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
, and let
![]() $\unicode[STIX]{x1D707}^{\prime }\in \unicode[STIX]{x1D6EC}$
. If
$\unicode[STIX]{x1D707}^{\prime }\in \unicode[STIX]{x1D6EC}$
. If
![]() $X$
is slope divisible with respect to
$X$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}^{\prime }$
, then
$\unicode[STIX]{x1D707}^{\prime }$
, then
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
is slope divisible with respect to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}^{\prime }$
. If
$\unicode[STIX]{x1D707}^{\prime }$
. If
![]() $X$
is a minimal
$X$
is a minimal
![]() $p$
-divisible group, then so is
$p$
-divisible group, then so is
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
.
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
.
Proof. It suffices to show this over an algebraically closed field. Let
![]() $M$
be the Dieudonné module of
$M$
be the Dieudonné module of
![]() $X$
. Write
$X$
. Write
![]() $v_{\unicode[STIX]{x1D707}}=(s,r)$
and
$v_{\unicode[STIX]{x1D707}}=(s,r)$
and
![]() $v_{\unicode[STIX]{x1D707}}^{\prime }=(s^{\prime },r^{\prime })$
. Obviously, if
$v_{\unicode[STIX]{x1D707}}^{\prime }=(s^{\prime },r^{\prime })$
. Obviously, if
![]() $p^{-r^{\prime }}V^{s^{\prime }}M\subset M$
, then
$p^{-r^{\prime }}V^{s^{\prime }}M\subset M$
, then
![]() $p^{-r^{\prime }}V^{s^{\prime }}N\subset N$
for
$p^{-r^{\prime }}V^{s^{\prime }}N\subset N$
for
![]() $N=p^{s-r}M+F^{s}M$
. The second assertion follows from Proposition 3.12.◻
$N=p^{s-r}M+F^{s}M$
. The second assertion follows from Proposition 3.12.◻
We collect some basic properties of the operators
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(-)$
for
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(-)$
for
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
.
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
.
Lemma 3.19. Let
![]() $X$
be a
$X$
be a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $K$
.
$K$
.
(1) We have
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X))=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X))$
for
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X))=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X))$
for
 $\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime }\in \unicode[STIX]{x1D6EC}_{+}$
.
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime }\in \unicode[STIX]{x1D6EC}_{+}$
.(2) Let
 $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
. Letbe an exact sequence of
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
. Letbe an exact sequence of
 $p$
-divisible groups over
$p$
-divisible groups over
 $K$
that splits over
$K$
that splits over
 $\overline{K}$
. Then,
$\overline{K}$
. Then,
 $Y\rightarrow X$
induces a monomorphism
$Y\rightarrow X$
induces a monomorphism
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y)\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
, and we have a canonical isomorphism
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y)\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
, and we have a canonical isomorphism  $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Z)\simeq \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)/\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Z)\simeq \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)/\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y).\end{eqnarray}$$
Proof. (1) Consider the natural isogenies
![]() $X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X))$
and
$X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X))$
and
![]() $X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X))$
. (The former is the composition of
$X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X))$
. (The former is the composition of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}^{\prime }}$
on
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}^{\prime }}$
on
![]() $X$
and
$X$
and
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
on
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X)$
, and the latter is obtained by exchanging the roles of
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X)$
, and the latter is obtained by exchanging the roles of
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $\unicode[STIX]{x1D707}^{\prime }$
.) We claim that those kernels are the same. It suffices to see this over
$\unicode[STIX]{x1D707}^{\prime }$
.) We claim that those kernels are the same. It suffices to see this over
![]() $\overline{K}$
. Let
$\overline{K}$
. Let
![]() $M=\mathbb{D}(X_{\overline{K}})$
, and set
$M=\mathbb{D}(X_{\overline{K}})$
, and set
![]() $U_{\unicode[STIX]{x1D707}}=p^{-r}V^{s}$
for
$U_{\unicode[STIX]{x1D707}}=p^{-r}V^{s}$
for
![]() $v_{\unicode[STIX]{x1D707}}=(s,r)$
. The claim over
$v_{\unicode[STIX]{x1D707}}=(s,r)$
. The claim over
![]() $\overline{K}$
follows from the equality
$\overline{K}$
follows from the equality
(2) Since the kernel of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:Y\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y)$
is contained in the kernel of
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:Y\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y)$
is contained in the kernel of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
, we have a homomorphism
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
, we have a homomorphism
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y)\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
. It suffices to show that this is a monomorphism over
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y)\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)$
. It suffices to show that this is a monomorphism over
![]() $\overline{K}$
. We may assume
$\overline{K}$
. We may assume
![]() $X_{\overline{K}}=Y_{\overline{K}}\times Z_{\overline{K}}$
. Then,
$X_{\overline{K}}=Y_{\overline{K}}\times Z_{\overline{K}}$
. Then,
Hence, obviously,
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y_{\overline{K}})\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X_{\overline{K}})$
is a monomorphism.
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y_{\overline{K}})\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X_{\overline{K}})$
is a monomorphism.
Note that
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
on
![]() $X$
and that on
$X$
and that on
![]() $Y$
induce an isogeny
$Y$
induce an isogeny
![]() $\unicode[STIX]{x1D717}:Z\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)/\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y)$
. It is sufficient to show that the kernel of
$\unicode[STIX]{x1D717}:Z\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X)/\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y)$
. It is sufficient to show that the kernel of
![]() $\unicode[STIX]{x1D717}$
is the same as the kernel of
$\unicode[STIX]{x1D717}$
is the same as the kernel of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:Z\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Z)$
. This follows from the fact that over
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:Z\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Z)$
. This follows from the fact that over
![]() $\overline{K}$
there is a canonical isomorphism
$\overline{K}$
there is a canonical isomorphism
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Z_{\overline{K}})\simeq \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X_{\overline{K}})/\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y_{\overline{K}})$
, which is obtained from (19).◻
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Z_{\overline{K}})\simeq \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X_{\overline{K}})/\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Y_{\overline{K}})$
, which is obtained from (19).◻
From now on, for
![]() $\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime }\in \unicode[STIX]{x1D6EC}_{+}$
, we write
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime }\in \unicode[STIX]{x1D6EC}_{+}$
, we write
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X)$
for
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X)$
for
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X))$
and
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}^{\prime }}(X))$
and
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{2}(X)$
for
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{2}(X)$
for
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X))$
, and so on.
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(X))$
, and so on.
In [Reference Zink19, Lemma 9] and the argument following it, Zink explicitly constructed an isogeny from a given
![]() $p$
-divisible group
$p$
-divisible group
![]() $X$
over
$X$
over
![]() $K$
to a
$K$
to a
![]() $p$
-divisible group that is slope divisible with respect to the smallest slope of
$p$
-divisible group that is slope divisible with respect to the smallest slope of
![]() $X$
. In the next lemma, we generalize this a little for later use.
$X$
. In the next lemma, we generalize this a little for later use.
Lemma 3.20. Let
![]() $X$
be a
$X$
be a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $K$
of height
$K$
of height
![]() $h$
. Let
$h$
. Let
![]() $\unicode[STIX]{x1D707}$
be an element of
$\unicode[STIX]{x1D707}$
be an element of
![]() $\unicode[STIX]{x1D6EC}_{+}$
whose slope is less than or equal to the smallest slope of
$\unicode[STIX]{x1D6EC}_{+}$
whose slope is less than or equal to the smallest slope of
![]() $X$
. Then,
$X$
. Then,
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X)$
is slope divisible with respect to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X)$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}$
. In particular, if
$\unicode[STIX]{x1D707}$
. In particular, if
![]() $X$
is isoclinic of slope
$X$
is isoclinic of slope
![]() $\unicode[STIX]{x1D706}$
, then
$\unicode[STIX]{x1D706}$
, then
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}}^{h-1}(X)$
is minimal for
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}}^{h-1}(X)$
is minimal for
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
with
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}_{+}$
with
![]() $\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle =1$
.
$\langle v_{\unicode[STIX]{x1D707}},v_{\unicode[STIX]{x1D706}}\rangle =1$
.
Proof. If suffices to show this over an algebraically closed field. Let
![]() $M$
be the Dieudonné module of
$M$
be the Dieudonné module of
![]() $X$
. Write
$X$
. Write
![]() $v_{\unicode[STIX]{x1D707}}=(s,r)$
, and set
$v_{\unicode[STIX]{x1D707}}=(s,r)$
, and set
![]() $U_{\unicode[STIX]{x1D707}}=p^{-r}V^{s}$
. The Dieudonné module
$U_{\unicode[STIX]{x1D707}}=p^{-r}V^{s}$
. The Dieudonné module
![]() $\mathbb{D}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X))$
of
$\mathbb{D}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X))$
of
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X)$
is isomorphic to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X)$
is isomorphic to
We have
![]() $U_{\unicode[STIX]{x1D707}}\mathbb{D}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X))\subset \mathbb{D}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X))$
, since the proof of [Reference Zink19, Lemma 9] works without change. Thus, we obtain the first assertion. The second one follows from Lemma 3.18 and Proposition 3.12.◻
$U_{\unicode[STIX]{x1D707}}\mathbb{D}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X))\subset \mathbb{D}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X))$
, since the proof of [Reference Zink19, Lemma 9] works without change. Thus, we obtain the first assertion. The second one follows from Lemma 3.18 and Proposition 3.12.◻
The following bi-divisible variant of Lemma 3.20 plays an important role in the proof of our main results.
Lemma 3.21. Let
![]() $X,Y,Z$
and
$X,Y,Z$
and
![]() $\unicode[STIX]{x1D707}$
be as in Proposition 3.17. Let
$\unicode[STIX]{x1D707}$
be as in Proposition 3.17. Let
![]() $h$
be the height of
$h$
be the height of
![]() $X$
. Then,
$X$
. Then,
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(Y)$
in
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(Y)$
in
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X)$
is slope bi-divisible with respect to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(X)$
is slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}$
.
$\unicode[STIX]{x1D707}$
.
Proof. It is sufficient to show this over an algebraically closed field. We may assume
![]() $X=Y\times Z$
. Applying Lemma 3.20 to
$X=Y\times Z$
. Applying Lemma 3.20 to
![]() $Y$
, we have that
$Y$
, we have that
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(Y)$
is slope divisible with respect to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(Y)$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}$
. It remains to show that
$\unicode[STIX]{x1D707}$
. It remains to show that
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(Z)$
is slope divisible with respect to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(Z)$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}^{\ast }$
. Let
$\unicode[STIX]{x1D707}^{\ast }$
. Let
![]() $N$
be the Dieudonné module of
$N$
be the Dieudonné module of
![]() $Z$
. The Dieudonné module of
$Z$
. The Dieudonné module of
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Z)$
is
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}(Z)$
is
![]() $p^{-r}V^{s}N+N$
, which is isomorphic to
$p^{-r}V^{s}N+N$
, which is isomorphic to
![]() $N+U_{\unicode[STIX]{x1D707}^{\ast }}N$
, where
$N+U_{\unicode[STIX]{x1D707}^{\ast }}N$
, where
![]() $U_{\unicode[STIX]{x1D707}^{\ast }}=(p^{-r}V^{s})^{-1}=p^{-(s-r)}F^{s}$
. Hence, the Dieudonné module
$U_{\unicode[STIX]{x1D707}^{\ast }}=(p^{-r}V^{s})^{-1}=p^{-(s-r)}F^{s}$
. Hence, the Dieudonné module
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(Z)$
is isomorphic to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{h-1}(Z)$
is isomorphic to
One can show that this is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}^{\ast }$
, in the same way as in Lemma 3.20, considering
$\unicode[STIX]{x1D707}^{\ast }$
, in the same way as in Lemma 3.20, considering
![]() $\operatorname{Ver}$
-slope instead of slope (
$\operatorname{Ver}$
-slope instead of slope (
![]() $=\operatorname{Fr}$
-slope).◻
$=\operatorname{Fr}$
-slope).◻
The next proposition is used in induction steps when we construct an isogeny from a given
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $K$
to a completely slope bi-divisible
$K$
to a completely slope bi-divisible
![]() $p$
-divisible group.
$p$
-divisible group.
Proposition 3.22. Let
![]() $X$
be a partially completely slope bi-divisible
$X$
be a partially completely slope bi-divisible
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $K$
with respect to
$K$
with respect to
![]() $\unicode[STIX]{x1D707}_{2},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
with filtration
$\unicode[STIX]{x1D707}_{2},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
with filtration
Let
![]() $\unicode[STIX]{x1D707}_{1}$
be an element of
$\unicode[STIX]{x1D707}_{1}$
be an element of
![]() $\unicode[STIX]{x1D6EC}_{+}$
whose slope is greater than
$\unicode[STIX]{x1D6EC}_{+}$
whose slope is greater than
![]() $\overline{\unicode[STIX]{x1D707}_{2}}$
and is less than or equal to the smallest slope of
$\overline{\unicode[STIX]{x1D707}_{2}}$
and is less than or equal to the smallest slope of
![]() $X_{1}$
. Let
$X_{1}$
. Let
![]() $e$
be a nonnegative integer such that
$e$
be a nonnegative integer such that
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X_{1}$
in
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X_{1}$
in
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X$
is slope bi-divisible with respect to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X$
is slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1}$
. (Lemma 3.21 says that
$\unicode[STIX]{x1D707}_{1}$
. (Lemma 3.21 says that
![]() $e=h-1$
satisfies this condition.) Then,
$e=h-1$
satisfies this condition.) Then,
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X$
is partially completely slope bi-divisible with respect to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X$
is partially completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.
Proof. Set
![]() $Y:=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X$
and
$Y:=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X$
and
![]() $Y_{i}:=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X_{i}$
for
$Y_{i}:=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X_{i}$
for
![]() $i=1,\ldots ,\ell$
. As obtained in [Reference Zink19, (11) on p. 89], there is an exact sequence of
$i=1,\ldots ,\ell$
. As obtained in [Reference Zink19, (11) on p. 89], there is an exact sequence of
![]() $p$
-divisible groups
$p$
-divisible groups
where ![]() and
and
![]() $Y_{1}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}}-\text{nul}}$
are characterized by the property that
$Y_{1}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}}-\text{nul}}$
are characterized by the property that
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}}$
induces an isomorphism on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}}$
induces an isomorphism on ![]() and is nilpotent on
and is nilpotent on
![]() $Y_{1}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}}-\text{nul}}[p^{n}]$
for all
$Y_{1}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}}-\text{nul}}[p^{n}]$
for all
![]() $n$
. Put
$n$
. Put
![]() $Y_{0}:=Y_{1}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}}-\text{nul}}$
. We claim that
$Y_{0}:=Y_{1}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}_{1}}-\text{nul}}$
. We claim that
![]() $Y$
is partially completely slope bi-divisible with respect to
$Y$
is partially completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
with filtration
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
with filtration
We need to check that this filtration
![]() $Y_{\bullet }$
satisfies the conditions (i), (ii), (iii) in Definition 3.7.
$Y_{\bullet }$
satisfies the conditions (i), (ii), (iii) in Definition 3.7.
By the definition of
![]() $Y_{0}$
, all of the slopes of
$Y_{0}$
, all of the slopes of
![]() $Y_{0}$
are greater than
$Y_{0}$
are greater than
![]() $\overline{\unicode[STIX]{x1D707}_{1}}$
, whence
$\overline{\unicode[STIX]{x1D707}_{1}}$
, whence
![]() $Y_{\bullet }$
satisfies (iii).
$Y_{\bullet }$
satisfies (iii).
As
![]() $X_{j}$
(
$X_{j}$
(
![]() $j\leqslant i$
) are slope divisible with respect to
$j\leqslant i$
) are slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{i}$
for
$\unicode[STIX]{x1D707}_{i}$
for
![]() $2\leqslant i\leqslant \ell$
, so are
$2\leqslant i\leqslant \ell$
, so are
![]() $Y_{j}$
(
$Y_{j}$
(
![]() $j\leqslant i$
), by Lemma 3.18. By the assumption,
$j\leqslant i$
), by Lemma 3.18. By the assumption,
![]() $Y_{1}$
is slope divisible with respect to
$Y_{1}$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1}$
. As
$\unicode[STIX]{x1D707}_{1}$
. As
![]() $X_{1}$
is slope divisible with respect to
$X_{1}$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{i}$
(
$\unicode[STIX]{x1D707}_{i}$
(
![]() $i\geqslant 2$
), so is
$i\geqslant 2$
), so is
![]() $Y_{1}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X_{1}$
, by Lemma 3.18. Since
$Y_{1}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}X_{1}$
, by Lemma 3.18. Since
![]() $(Y_{0})_{\overline{K}}$
is a direct summand of
$(Y_{0})_{\overline{K}}$
is a direct summand of
![]() $(Y_{1})_{\overline{K}}$
, we have that
$(Y_{1})_{\overline{K}}$
, we have that
![]() $Y_{0}$
is slope divisible with respect to
$Y_{0}$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{i}$
(
$\unicode[STIX]{x1D707}_{i}$
(
![]() $i\geqslant 1$
). Hence,
$i\geqslant 1$
). Hence,
![]() $Y_{\bullet }$
satisfies (i).
$Y_{\bullet }$
satisfies (i).
By Lemma 3.19(2), the
![]() $p$
-divisible group
$p$
-divisible group
![]() $Y/Y_{j}$
is isomorphic to
$Y/Y_{j}$
is isomorphic to
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}(X/X_{j})$
for
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}(X/X_{j})$
for
![]() $j\geqslant 1$
. By Lemma 3.18,
$j\geqslant 1$
. By Lemma 3.18,
![]() $Y/Y_{j}\simeq \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}(X/X_{j})$
(
$Y/Y_{j}\simeq \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{1}}^{e}(X/X_{j})$
(
![]() $j\geqslant 1$
) is slope divisible with respect to
$j\geqslant 1$
) is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{i}^{\ast }$
for
$\unicode[STIX]{x1D707}_{i}^{\ast }$
for
![]() $i\leqslant j+1$
. Over the algebraic closure
$i\leqslant j+1$
. Over the algebraic closure
![]() $\overline{K}$
of
$\overline{K}$
of
![]() $K$
, we have
$K$
, we have
![]() $(Y/Y_{0})_{\overline{K}}\simeq (Y_{1}/Y_{0})_{\overline{K}}\oplus (Y/Y_{1})_{\overline{K}}$
. Since
$(Y/Y_{0})_{\overline{K}}\simeq (Y_{1}/Y_{0})_{\overline{K}}\oplus (Y/Y_{1})_{\overline{K}}$
. Since
![]() $(Y_{1}/Y_{0})_{\overline{K}}$
and
$(Y_{1}/Y_{0})_{\overline{K}}$
and
![]() $(Y/Y_{1})_{\overline{K}}$
are both slope divisible with respect to
$(Y/Y_{1})_{\overline{K}}$
are both slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1}^{\ast }$
, we have that
$\unicode[STIX]{x1D707}_{1}^{\ast }$
, we have that
![]() $(Y/Y_{0})_{\overline{K}}$
is slope divisible with respect to
$(Y/Y_{0})_{\overline{K}}$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1}^{\ast }$
and therefore so is
$\unicode[STIX]{x1D707}_{1}^{\ast }$
and therefore so is
![]() $Y/Y_{0}$
. Thus,
$Y/Y_{0}$
. Thus,
![]() $Y_{\bullet }$
satisfies (ii).◻
$Y_{\bullet }$
satisfies (ii).◻
Now we get the main result over a field of characteristic
![]() $p$
.
$p$
.
Corollary 3.23. Let
![]() $X$
be a
$X$
be a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $K$
of height
$K$
of height
![]() $h$
. Let
$h$
. Let
![]() $\unicode[STIX]{x1D706}_{1}>\unicode[STIX]{x1D706}_{2}>\cdots >\unicode[STIX]{x1D706}_{\ell }$
be the set of positive slopes of
$\unicode[STIX]{x1D706}_{1}>\unicode[STIX]{x1D706}_{2}>\cdots >\unicode[STIX]{x1D706}_{\ell }$
be the set of positive slopes of
![]() $X$
. Then, we have the following.
$X$
. Then, we have the following.
(1)
 $(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}_{i}}^{h-1})(X)$
is completely slope bi-divisible with respect to
$(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}_{i}}^{h-1})(X)$
is completely slope bi-divisible with respect to
 $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell },0$
.
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell },0$
.(2) We choose
 $\unicode[STIX]{x1D707}_{i}\in \unicode[STIX]{x1D6EC}_{+}$
such that
$\unicode[STIX]{x1D707}_{i}\in \unicode[STIX]{x1D6EC}_{+}$
such that
 $\langle v_{\unicode[STIX]{x1D707}_{i}},v_{\unicode[STIX]{x1D706}_{i}}\rangle =1$
. Then,
$\langle v_{\unicode[STIX]{x1D707}_{i}},v_{\unicode[STIX]{x1D706}_{i}}\rangle =1$
. Then,
 $(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{i}}^{h-1}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}_{i}}^{h-1})(X)$
is minimal.
$(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{i}}^{h-1}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}_{i}}^{h-1})(X)$
is minimal.
Here, recall that
![]() $\unicode[STIX]{x1D706}_{i}$
is regarded as the element
$\unicode[STIX]{x1D706}_{i}$
is regarded as the element
![]() $(\unicode[STIX]{x1D706}_{i},1)$
of
$(\unicode[STIX]{x1D706}_{i},1)$
of
![]() $\unicode[STIX]{x1D6EC}_{1}$
for each
$\unicode[STIX]{x1D6EC}_{1}$
for each
![]() $i=1,\ldots ,\ell$
.
$i=1,\ldots ,\ell$
.
Proof. It suffices to show these over the algebraic closure of
![]() $K$
. Therefore, we assume that
$K$
. Therefore, we assume that
![]() $K$
is algebraically closed. Then, as it suffices to show them for the formal part of
$K$
is algebraically closed. Then, as it suffices to show them for the formal part of
![]() $X$
, we may assume that
$X$
, we may assume that
![]() $X$
is a formal
$X$
is a formal
![]() $p$
-divisible group (i.e., every slope of
$p$
-divisible group (i.e., every slope of
![]() $X$
is positive).
$X$
is positive).
(1) By Proposition 3.22, inductively one can check that
![]() $(\prod _{i=j}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}_{i}}^{h-1})(X)$
is partially completely slope bi-divisible with respect to
$(\prod _{i=j}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}_{i}}^{h-1})(X)$
is partially completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D706}_{j},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
.
$\unicode[STIX]{x1D706}_{j},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
.
(2) Set
![]() $Y:=(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}_{i}}^{h-1})(X)$
. By (1),
$Y:=(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D706}_{i}}^{h-1})(X)$
. By (1),
![]() $Y$
is completely slope bi-divisible with respect to
$Y$
is completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
. Set
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
. Set
![]() $Z:=(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{i}}^{h-1})(Y)$
, which is also completely slope bi-divisible with respect to
$Z:=(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{i}}^{h-1})(Y)$
, which is also completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
. Since
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }$
. Since
![]() $\operatorname{Gr}_{j}(Y)$
is isoclinic and slope divisible with respect to
$\operatorname{Gr}_{j}(Y)$
is isoclinic and slope divisible with respect to
![]() $\unicode[STIX]{x1D706}_{j}$
, so is
$\unicode[STIX]{x1D706}_{j}$
, so is
![]() $\operatorname{Gr}_{j}(Z)=(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{i}}^{h-1})\operatorname{Gr}_{j}(Y)$
, by Lemma 3.18. Moreover,
$\operatorname{Gr}_{j}(Z)=(\prod _{i=1}^{\ell }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{i}}^{h-1})\operatorname{Gr}_{j}(Y)$
, by Lemma 3.18. Moreover,
![]() $\operatorname{Gr}_{j}(Z)=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{j}}^{h-1}(\prod _{i\neq j}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{i}}^{h-1}\operatorname{Gr}_{j}(Y))$
is slope divisible with respect to
$\operatorname{Gr}_{j}(Z)=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{j}}^{h-1}(\prod _{i\neq j}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}_{i}}^{h-1}\operatorname{Gr}_{j}(Y))$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D707}_{j}$
, by Lemma 3.20. Hence,
$\unicode[STIX]{x1D707}_{j}$
, by Lemma 3.20. Hence,
![]() $\operatorname{Gr}_{j}(Z)$
is minimal, by Proposition 3.12, and therefore so is
$\operatorname{Gr}_{j}(Z)$
is minimal, by Proposition 3.12, and therefore so is
![]() $Z$
.◻
$Z$
.◻
4 Proof
We start by proving our main result (Proposition 4.1) over a discrete valuation ring. Based on this result, we show the main theorem (Theorem 4.2).
The result over a discrete valuation ring is stated in terms of Raynaud’s flat extension. Let
![]() $R$
be a discrete valuation ring of characteristic
$R$
be a discrete valuation ring of characteristic
![]() $p$
. Let
$p$
. Let
![]() $K$
be the quotient ring of
$K$
be the quotient ring of
![]() $R$
. Let
$R$
. Let
![]() ${\mathcal{X}}$
be a
${\mathcal{X}}$
be a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $R$
. Write
$R$
. Write
![]() $X={\mathcal{X}}_{K}$
. Let
$X={\mathcal{X}}_{K}$
. Let
![]() $G$
be a finite subgroup scheme of
$G$
be a finite subgroup scheme of
![]() $X$
. This defines an isogeny
$X$
. This defines an isogeny
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y$
of
$\unicode[STIX]{x1D70C}:X\rightarrow Y$
of
![]() $p$
-divisible groups with
$p$
-divisible groups with
![]() $G=\ker (\unicode[STIX]{x1D70C})$
. Let
$G=\ker (\unicode[STIX]{x1D70C})$
. Let
![]() $N$
be a sufficiently large integer such that
$N$
be a sufficiently large integer such that
![]() $G\subset X[p^{N}]$
. Let
$G\subset X[p^{N}]$
. Let
![]() ${\mathcal{G}}$
be the schematic closure in
${\mathcal{G}}$
be the schematic closure in
![]() ${\mathcal{X}}[p^{N}]$
of
${\mathcal{X}}[p^{N}]$
of
![]() $G$
. Note that
$G$
. Note that
![]() ${\mathcal{G}}$
is a flat subgroup scheme of
${\mathcal{G}}$
is a flat subgroup scheme of
![]() ${\mathcal{X}}[p^{N}]$
(see [Reference Raynaud16, pp. 259–260]). By taking the quotient by
${\mathcal{X}}[p^{N}]$
(see [Reference Raynaud16, pp. 259–260]). By taking the quotient by
![]() ${\mathcal{G}}$
, we have an isogeny
${\mathcal{G}}$
, we have an isogeny
![]() $\tilde{\unicode[STIX]{x1D70C}}:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
. This construction of the isogeny
$\tilde{\unicode[STIX]{x1D70C}}:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
. This construction of the isogeny
![]() $\tilde{\unicode[STIX]{x1D70C}}:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
from given data
$\tilde{\unicode[STIX]{x1D70C}}:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
from given data
![]() $({\mathcal{X}},\unicode[STIX]{x1D70C}:X\rightarrow Y)$
is called the flat extension.
$({\mathcal{X}},\unicode[STIX]{x1D70C}:X\rightarrow Y)$
is called the flat extension.
An NP-quasi-saturated
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $(S,D)$
is defined by replacing saturated by quasi-saturated in the definition of an NP-saturated
$(S,D)$
is defined by replacing saturated by quasi-saturated in the definition of an NP-saturated
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $(S,D)$
. An NP-quasi-saturated
$(S,D)$
. An NP-quasi-saturated
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $R$
is that over
$R$
is that over
![]() $(S,D)$
with
$(S,D)$
with
![]() $S=\operatorname{Spec}(R)$
and
$S=\operatorname{Spec}(R)$
and
![]() $D=\operatorname{Spec}(k)$
, where
$D=\operatorname{Spec}(k)$
, where
![]() $k$
is the residue field of
$k$
is the residue field of
![]() $R$
.
$R$
.
Proposition 4.1. Let
![]() ${\mathcal{X}}$
be an NP-quasi-saturated
${\mathcal{X}}$
be an NP-quasi-saturated
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $R$
. Set
$R$
. Set
![]() $X={\mathcal{X}}_{K}$
. Let
$X={\mathcal{X}}_{K}$
. Let
![]() $\unicode[STIX]{x1D709}$
(resp.
$\unicode[STIX]{x1D709}$
(resp.
![]() $\unicode[STIX]{x1D701}$
) be the Newton polygon of
$\unicode[STIX]{x1D701}$
) be the Newton polygon of
![]() $X$
(resp.
$X$
(resp.
![]() ${\mathcal{X}}_{k}$
). Let
${\mathcal{X}}_{k}$
). Let
![]() $\{\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }\}$
be a subset of
$\{\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }\}$
be a subset of
![]() $\unicode[STIX]{x1D6EC}_{+}$
containing all slopes of
$\unicode[STIX]{x1D6EC}_{+}$
containing all slopes of
![]() $\unicode[STIX]{x1D701}$
such that
$\unicode[STIX]{x1D701}$
such that
![]() $\langle v_{\unicode[STIX]{x1D707}_{i}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}_{i}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}_{i}}(\unicode[STIX]{x1D701})\rangle \leqslant 1$
. Suppose that
$\langle v_{\unicode[STIX]{x1D707}_{i}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}_{i}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}_{i}}(\unicode[STIX]{x1D701})\rangle \leqslant 1$
. Suppose that
![]() $\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. Then, there exists an isogeny
$\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. Then, there exists an isogeny
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y$
over
$\unicode[STIX]{x1D70C}:X\rightarrow Y$
over
![]() $K$
whose flat extension
$K$
whose flat extension
![]() ${\mathcal{X}}\rightarrow {\mathcal{Y}}$
satisfies that
${\mathcal{X}}\rightarrow {\mathcal{Y}}$
satisfies that
![]() ${\mathcal{Y}}_{K}$
is minimal and
${\mathcal{Y}}_{K}$
is minimal and
![]() ${\mathcal{Y}}_{k}$
is completely slope bi-divisible with respect to
${\mathcal{Y}}_{k}$
is completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
. Moreover, the isogeny
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
. Moreover, the isogeny
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y$
can be taken as a composition of
$\unicode[STIX]{x1D70C}:X\rightarrow Y$
can be taken as a composition of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}_{i}}$
s for
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}_{i}}$
s for
![]() $1\leqslant i\leqslant \ell$
. (See (18) for the definition of
$1\leqslant i\leqslant \ell$
. (See (18) for the definition of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
.)
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}$
.)
Proof. We first reduce to the case where
![]() $X$
is minimal. If the theorem is true for minimal
$X$
is minimal. If the theorem is true for minimal
![]() $X^{\prime }$
, choose an isogeny
$X^{\prime }$
, choose an isogeny
![]() $X\rightarrow X^{\prime }$
with
$X\rightarrow X^{\prime }$
with
![]() $X^{\prime }$
minimal (Corollary 3.23(2)), and let
$X^{\prime }$
minimal (Corollary 3.23(2)), and let
![]() $X^{\prime }\rightarrow Y$
be an isogeny obtained from the theorem for
$X^{\prime }\rightarrow Y$
be an isogeny obtained from the theorem for
![]() $X^{\prime }$
; then, the composition
$X^{\prime }$
; then, the composition
![]() $\unicode[STIX]{x1D70C}:X\rightarrow X^{\prime }\rightarrow Y$
satisfies the properties of the theorem.
$\unicode[STIX]{x1D70C}:X\rightarrow X^{\prime }\rightarrow Y$
satisfies the properties of the theorem.
Therefore, we assume that
![]() $X$
is minimal. It suffices to show that if
$X$
is minimal. It suffices to show that if
![]() ${\mathcal{X}}_{\overline{k}}$
is partially completely slope bi-divisible with respect to
${\mathcal{X}}_{\overline{k}}$
is partially completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{i+1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
, then there exists an isogeny
$\unicode[STIX]{x1D707}_{i+1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
, then there exists an isogeny
![]() $X\rightarrow Y$
such that
$X\rightarrow Y$
such that
![]() $Y$
is minimal and
$Y$
is minimal and
![]() ${\mathcal{Y}}_{\overline{k}}$
is partially completely slope bi-divisible with respect to
${\mathcal{Y}}_{\overline{k}}$
is partially completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{i},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.
$\unicode[STIX]{x1D707}_{i},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.
Set
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{i}$
, and write
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{i}$
, and write
![]() $v_{\unicode[STIX]{x1D707}}=(s,r)$
. Let
$v_{\unicode[STIX]{x1D707}}=(s,r)$
. Let
![]() $\text{}\underline{{\mathcal{G}}}$
be the fppf sheaf obtained as the sheafification of the functor sending an
$\text{}\underline{{\mathcal{G}}}$
be the fppf sheaf obtained as the sheafification of the functor sending an
![]() $R$
-algebra
$R$
-algebra
![]() $A$
to
$A$
to
For an
![]() $R$
-algebra
$R$
-algebra
![]() $S$
, let
$S$
, let
![]() $\text{}\underline{{\mathcal{G}}}_{S}$
be the functor obtained by restricting
$\text{}\underline{{\mathcal{G}}}_{S}$
be the functor obtained by restricting
![]() $\text{}\underline{{\mathcal{G}}}$
to
$\text{}\underline{{\mathcal{G}}}$
to
![]() $S$
-algebras. Note that
$S$
-algebras. Note that
![]() $\text{}\underline{{\mathcal{G}}}_{k}$
(resp.
$\text{}\underline{{\mathcal{G}}}_{k}$
(resp.
![]() $\text{}\underline{{\mathcal{G}}}_{K}$
) is represented by a finite group scheme
$\text{}\underline{{\mathcal{G}}}_{K}$
) is represented by a finite group scheme
![]() ${\mathcal{G}}_{k}$
(resp.
${\mathcal{G}}_{k}$
(resp.
![]() ${\mathcal{G}}_{K}$
). We see from Lemma 3.14 that
${\mathcal{G}}_{K}$
). We see from Lemma 3.14 that
![]() ${\mathcal{G}}_{k}$
(resp.
${\mathcal{G}}_{k}$
(resp.
![]() ${\mathcal{G}}_{K}$
) is the kernel of
${\mathcal{G}}_{K}$
) is the kernel of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:{\mathcal{X}}_{k}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{k})$
(resp.
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:{\mathcal{X}}_{k}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{k})$
(resp.
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:{\mathcal{X}}_{K}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{K})$
). Set
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D707}}:{\mathcal{X}}_{K}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{K})$
). Set
By the upper-semicontinuity for the structure sheaf of
![]() ${\mathcal{H}}$
, we have
${\mathcal{H}}$
, we have
We claim that
![]() $\operatorname{rk}{\mathcal{G}}_{k}=\operatorname{rk}{\mathcal{G}}_{K}$
if
$\operatorname{rk}{\mathcal{G}}_{k}=\operatorname{rk}{\mathcal{G}}_{K}$
if
![]() $({\mathcal{X}}_{k})_{i}$
in
$({\mathcal{X}}_{k})_{i}$
in
![]() ${\mathcal{X}}_{k}$
is not slope bi-divisible with respect to
${\mathcal{X}}_{k}$
is not slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}$
. By Proposition 3.17 for
$\unicode[STIX]{x1D707}$
. By Proposition 3.17 for
![]() ${\mathcal{X}}_{K}$
, we have
${\mathcal{X}}_{K}$
, we have
Also, by Proposition 3.17 again, we get
where the equality holds if and only if
![]() $({\mathcal{X}}_{k})_{i}$
in
$({\mathcal{X}}_{k})_{i}$
in
![]() ${\mathcal{X}}_{k}$
is slope bi-divisible with respect to
${\mathcal{X}}_{k}$
is slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}$
. By our assumption, the difference of the right-hand sides of (22) and (23) is at most one:
$\unicode[STIX]{x1D707}$
. By our assumption, the difference of the right-hand sides of (22) and (23) is at most one:
Clearly, (21)–(24) imply the claim.
If
![]() $\operatorname{rk}{\mathcal{G}}_{k}=\operatorname{rk}{\mathcal{G}}_{K}$
, then
$\operatorname{rk}{\mathcal{G}}_{k}=\operatorname{rk}{\mathcal{G}}_{K}$
, then
![]() ${\mathcal{H}}$
is flat over
${\mathcal{H}}$
is flat over
![]() $R$
, whence
$R$
, whence
![]() $\text{}\underline{{\mathcal{G}}}$
is represented by a finite flat group scheme
$\text{}\underline{{\mathcal{G}}}$
is represented by a finite flat group scheme
![]() ${\mathcal{G}}$
that is isomorphic to the quotient
${\mathcal{G}}$
that is isomorphic to the quotient
![]() ${\mathcal{X}}^{(p^{s})}[p^{s-r}]/{\mathcal{H}}$
(cf. [Reference Demazure and Grothendieck1, Example V]). Putting
${\mathcal{X}}^{(p^{s})}[p^{s-r}]/{\mathcal{H}}$
(cf. [Reference Demazure and Grothendieck1, Example V]). Putting
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})={\mathcal{X}}/{\mathcal{G}}$
, we have the canonical isogeny
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})={\mathcal{X}}/{\mathcal{G}}$
, we have the canonical isogeny
![]() ${\mathcal{X}}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})$
. Note that
${\mathcal{X}}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})$
. Note that
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})_{k}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{k})$
and
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})_{k}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{k})$
and
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})_{K}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{K})$
.
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})_{K}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{K})$
.
This argument can be applied to
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})$
if
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}})$
if
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{k})_{i}$
in
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{k})_{i}$
in
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{k})$
is not slope bi-divisible with respect to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}({\mathcal{X}}_{k})$
is not slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}$
. Repeating this argument, we have the sequence of isogenies
$\unicode[STIX]{x1D707}$
. Repeating this argument, we have the sequence of isogenies
where
![]() $e$
is the smallest nonnegative integer such that
$e$
is the smallest nonnegative integer such that
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{e}({\mathcal{X}}_{k})_{i}$
in
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{e}({\mathcal{X}}_{k})_{i}$
in
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{e}({\mathcal{X}}_{k})$
is slope bi-divisible with respect to
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{e}({\mathcal{X}}_{k})$
is slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}$
. Here, we use Lemma 3.21 for the existence of
$\unicode[STIX]{x1D707}$
. Here, we use Lemma 3.21 for the existence of
![]() $e$
. This sequence is obtained by the flat extension of
$e$
. This sequence is obtained by the flat extension of
where all
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{i}(X)$
are minimal. Let
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{i}(X)$
are minimal. Let
![]() $X\rightarrow Y$
be the isogeny
$X\rightarrow Y$
be the isogeny
![]() $X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{e}(X)$
. Then, its flat extension
$X\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{e}(X)$
. Then, its flat extension
![]() ${\mathcal{X}}\rightarrow {\mathcal{Y}}$
coincides with
${\mathcal{X}}\rightarrow {\mathcal{Y}}$
coincides with
![]() ${\mathcal{X}}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{e}({\mathcal{X}})$
. It follows from Proposition 3.22 that
${\mathcal{X}}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D707}}^{e}({\mathcal{X}})$
. It follows from Proposition 3.22 that
![]() ${\mathcal{Y}}_{\overline{k}}$
is partially completely slope bi-divisible with respect to
${\mathcal{Y}}_{\overline{k}}$
is partially completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{i},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.◻
$\unicode[STIX]{x1D707}_{i},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.◻
We generalize Proposition 4.1 to the case of general
![]() $(S,D)$
, using the same technique as in [Reference Oort and Zink13].
$(S,D)$
, using the same technique as in [Reference Oort and Zink13].
Theorem 4.2. Let
![]() $S$
be an integral Noetherian scheme with prime Weil divisor
$S$
be an integral Noetherian scheme with prime Weil divisor
![]() $D$
. Assume that
$D$
. Assume that
![]() $S$
is regular at the generic point of
$S$
is regular at the generic point of
![]() $D$
. Let
$D$
. Let
![]() ${\mathcal{X}}$
be an NP-quasi-saturated
${\mathcal{X}}$
be an NP-quasi-saturated
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $(S,D)$
. Let
$(S,D)$
. Let
![]() $\unicode[STIX]{x1D709}$
(resp.
$\unicode[STIX]{x1D709}$
(resp.
![]() $\unicode[STIX]{x1D701}$
) be the Newton polygon of
$\unicode[STIX]{x1D701}$
) be the Newton polygon of
![]() ${\mathcal{X}}_{S\setminus D}$
(resp.
${\mathcal{X}}_{S\setminus D}$
(resp.
![]() ${\mathcal{X}}_{D}$
). Let
${\mathcal{X}}_{D}$
). Let
![]() $\{\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }\}$
be a subset of
$\{\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }\}$
be a subset of
![]() $\unicode[STIX]{x1D6EC}_{+}$
containing all slopes of
$\unicode[STIX]{x1D6EC}_{+}$
containing all slopes of
![]() $\unicode[STIX]{x1D701}$
such that
$\unicode[STIX]{x1D701}$
such that
![]() $\langle v_{\unicode[STIX]{x1D707}_{i}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}_{i}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}_{i}}(\unicode[STIX]{x1D701})\rangle \leqslant 1$
. Suppose that
$\langle v_{\unicode[STIX]{x1D707}_{i}},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}_{i}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}_{i}}(\unicode[STIX]{x1D701})\rangle \leqslant 1$
. Suppose that
![]() $\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. Then, there is a finite birational morphism
$\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. Then, there is a finite birational morphism
![]() $\unicode[STIX]{x1D70B}:T\rightarrow S$
such that
$\unicode[STIX]{x1D70B}:T\rightarrow S$
such that
![]() ${\mathcal{X}}_{T}$
is isogenous to a
${\mathcal{X}}_{T}$
is isogenous to a
![]() $p$
-divisible group
$p$
-divisible group
![]() ${\mathcal{Y}}$
over
${\mathcal{Y}}$
over
![]() $T$
such that all of the geometric fibers over
$T$
such that all of the geometric fibers over
![]() $T\setminus \unicode[STIX]{x1D70B}^{-1}(D)$
are minimal and
$T\setminus \unicode[STIX]{x1D70B}^{-1}(D)$
are minimal and
![]() ${\mathcal{Y}}_{\unicode[STIX]{x1D70B}^{-1}D}$
is completely slope bi-divisible with respect to
${\mathcal{Y}}_{\unicode[STIX]{x1D70B}^{-1}D}$
is completely slope bi-divisible with respect to
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
.
Proof. Let
![]() $\unicode[STIX]{x1D702}$
be the generic point of
$\unicode[STIX]{x1D702}$
be the generic point of
![]() $D$
. Let
$D$
. Let
![]() $R={\mathcal{O}}_{S,\unicode[STIX]{x1D702}}$
, and let
$R={\mathcal{O}}_{S,\unicode[STIX]{x1D702}}$
, and let
![]() $K=\operatorname{frac}(R)$
. Set
$K=\operatorname{frac}(R)$
. Set
![]() $X={\mathcal{X}}_{K}$
. Let
$X={\mathcal{X}}_{K}$
. Let
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y$
be the isogeny over
$\unicode[STIX]{x1D70C}:X\rightarrow Y$
be the isogeny over
![]() $K$
constructed in Proposition 4.1.
$K$
constructed in Proposition 4.1.
Let
![]() $G$
be the kernel of
$G$
be the kernel of
![]() $\unicode[STIX]{x1D70C}$
, and let
$\unicode[STIX]{x1D70C}$
, and let
![]() $\overline{G}$
be the scheme-theoretic image of
$\overline{G}$
be the scheme-theoretic image of
![]() $G\rightarrow {\mathcal{X}}[p^{N}]$
for sufficient large
$G\rightarrow {\mathcal{X}}[p^{N}]$
for sufficient large
![]() $N$
. Let
$N$
. Let
![]() $V$
be the largest open subvariety such that
$V$
be the largest open subvariety such that
![]() $\overline{G}$
is flat over
$\overline{G}$
is flat over
![]() $V$
. Note that
$V$
. Note that
![]() $V$
contains the generic point
$V$
contains the generic point
![]() $\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D702}$
of
![]() $D$
. We have the
$D$
. We have the
![]() $p$
-divisible group
$p$
-divisible group
![]() ${\mathcal{Y}}^{\prime }:={\mathcal{X}}_{V}/\overline{G}_{V}$
over
${\mathcal{Y}}^{\prime }:={\mathcal{X}}_{V}/\overline{G}_{V}$
over
![]() $V$
with isogeny
$V$
with isogeny
Let
![]() $d$
be the degree of
$d$
be the degree of
![]() $\unicode[STIX]{x1D70C}$
. We make use of the moduli space
$\unicode[STIX]{x1D70C}$
. We make use of the moduli space
![]() ${\mathcal{M}}$
of isogenies from
${\mathcal{M}}$
of isogenies from
![]() ${\mathcal{X}}$
of degree
${\mathcal{X}}$
of degree
![]() $d$
. This is defined to be the scheme over
$d$
. This is defined to be the scheme over
![]() $S$
representing the following functor
$S$
representing the following functor
![]() $\text{}\underline{{\mathcal{M}}}$
from the category of
$\text{}\underline{{\mathcal{M}}}$
from the category of
![]() $S$
-schemes to that of sets. For an
$S$
-schemes to that of sets. For an
![]() $S$
-scheme
$S$
-scheme
![]() $T$
, an element of
$T$
, an element of
![]() $\text{}\underline{{\mathcal{M}}}(T)$
is the isomorphism class of an isogeny
$\text{}\underline{{\mathcal{M}}}(T)$
is the isomorphism class of an isogeny
![]() ${\mathcal{X}}_{T}\rightarrow Z$
of degree
${\mathcal{X}}_{T}\rightarrow Z$
of degree
![]() $d$
over
$d$
over
![]() $T$
, where
$T$
, where
![]() $Z$
is a
$Z$
is a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $T$
. It is known that
$T$
. It is known that
![]() $\text{}\underline{{\mathcal{M}}}$
is represented by a projective scheme
$\text{}\underline{{\mathcal{M}}}$
is represented by a projective scheme
![]() ${\mathcal{M}}$
over
${\mathcal{M}}$
over
![]() $S$
(see [Reference Oort and Zink13, 2.3]).
$S$
(see [Reference Oort and Zink13, 2.3]).
Now,
![]() $\unicode[STIX]{x1D70C}^{\prime }$
defines a morphism
$\unicode[STIX]{x1D70C}^{\prime }$
defines a morphism
![]() $V\rightarrow {\mathcal{M}}$
commuting the diagram
$V\rightarrow {\mathcal{M}}$
commuting the diagram

Let
![]() $\tilde{S}$
be the scheme-theoretic image of
$\tilde{S}$
be the scheme-theoretic image of
![]() $V$
in
$V$
in
![]() ${\mathcal{M}}$
. Then, we have a morphism
${\mathcal{M}}$
. Then, we have a morphism
![]() $f:\tilde{S}\rightarrow S$
, which is proper, surjective and birational. The inclusion
$f:\tilde{S}\rightarrow S$
, which is proper, surjective and birational. The inclusion
![]() $\tilde{S}\subset {\mathcal{M}}$
defines an isogeny
$\tilde{S}\subset {\mathcal{M}}$
defines an isogeny
![]() ${\mathcal{X}}_{\tilde{S}}\rightarrow {\mathcal{Y}}^{\prime \prime }$
over
${\mathcal{X}}_{\tilde{S}}\rightarrow {\mathcal{Y}}^{\prime \prime }$
over
![]() $\tilde{S}$
. Since
$\tilde{S}$
. Since
![]() ${\mathcal{Y}}^{\prime \prime }$
is minimal over the generic point of
${\mathcal{Y}}^{\prime \prime }$
is minimal over the generic point of
![]() $\tilde{S}\setminus f^{-1}(D)$
, by Corollary 3.13,
$\tilde{S}\setminus f^{-1}(D)$
, by Corollary 3.13,
![]() ${\mathcal{Y}}^{\prime \prime }$
is minimal over
${\mathcal{Y}}^{\prime \prime }$
is minimal over
![]() $\tilde{S}\setminus f^{-1}(D)$
. Moreover,
$\tilde{S}\setminus f^{-1}(D)$
. Moreover,
![]() ${\mathcal{Y}}_{f^{-1}(D)}^{\prime \prime }$
is completely slope bi-divisible over every generic point, and therefore
${\mathcal{Y}}_{f^{-1}(D)}^{\prime \prime }$
is completely slope bi-divisible over every generic point, and therefore
![]() ${\mathcal{Y}}_{f^{-1}(D)}^{\prime \prime }$
is completely slope bi-divisible, by Lemma 3.11.
${\mathcal{Y}}_{f^{-1}(D)}^{\prime \prime }$
is completely slope bi-divisible, by Lemma 3.11.
Let
be the Stein factorization with
![]() $f_{\ast }{\mathcal{O}}_{\tilde{S}}={\mathcal{O}}_{T}$
. Let
$f_{\ast }{\mathcal{O}}_{\tilde{S}}={\mathcal{O}}_{T}$
. Let
![]() $x\in T$
, and let
$x\in T$
, and let
![]() $\tilde{S}_{x}$
be the fiber over
$\tilde{S}_{x}$
be the fiber over
![]() $x$
of
$x$
of
![]() $\tilde{S}\rightarrow T$
. By [Reference Oort and Zink13, Lemma 2.5], the image of
$\tilde{S}\rightarrow T$
. By [Reference Oort and Zink13, Lemma 2.5], the image of
![]() $\tilde{S}_{\overline{x}}\rightarrow {\mathcal{M}}$
is finite. Since
$\tilde{S}_{\overline{x}}\rightarrow {\mathcal{M}}$
is finite. Since
![]() $\tilde{S}_{\overline{x}}$
is connected, the image is a single point of
$\tilde{S}_{\overline{x}}$
is connected, the image is a single point of
![]() ${\mathcal{M}}$
. From [Reference Oort and Zink13, Lemma 2.6], we have a morphism
${\mathcal{M}}$
. From [Reference Oort and Zink13, Lemma 2.6], we have a morphism
![]() $T\rightarrow {\mathcal{M}}$
. This defines a desired isogeny
$T\rightarrow {\mathcal{M}}$
. This defines a desired isogeny
over
![]() $T$
.◻
$T$
.◻
The next corollary is the result in the NP-saturated case, from which Corollary 1.1 follows immediately.
Corollary 4.3. Let
![]() $S,D$
be as in Theorem 4.2. Let
$S,D$
be as in Theorem 4.2. Let
![]() ${\mathcal{X}}$
be an NP-saturated
${\mathcal{X}}$
be an NP-saturated
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $(S,D)$
. Then, there is a finite birational morphism
$(S,D)$
. Then, there is a finite birational morphism
![]() $T\rightarrow S$
such that
$T\rightarrow S$
such that
![]() ${\mathcal{X}}_{T}$
is isogenous to a
${\mathcal{X}}_{T}$
is isogenous to a
![]() $p$
-divisible group
$p$
-divisible group
![]() ${\mathcal{Y}}$
over
${\mathcal{Y}}$
over
![]() $T$
whose geometric fibers are all minimal.
$T$
whose geometric fibers are all minimal.
Proof. Let
![]() $\unicode[STIX]{x1D709}$
(resp.
$\unicode[STIX]{x1D709}$
(resp.
![]() $\unicode[STIX]{x1D701}$
) be the Newton polygon of
$\unicode[STIX]{x1D701}$
) be the Newton polygon of
![]() ${\mathcal{X}}_{S\setminus D}$
(resp.
${\mathcal{X}}_{S\setminus D}$
(resp.
![]() ${\mathcal{X}}_{D}$
). As in (5), we write
${\mathcal{X}}_{D}$
). As in (5), we write
so that
![]() $\unicode[STIX]{x1D701}^{\prime }\prec \unicode[STIX]{x1D709}^{\prime }$
is saturated and
$\unicode[STIX]{x1D701}^{\prime }\prec \unicode[STIX]{x1D709}^{\prime }$
is saturated and
![]() $\unicode[STIX]{x1D709}^{\prime }$
consists of only two segments. Let
$\unicode[STIX]{x1D709}^{\prime }$
consists of only two segments. Let
![]() $a$
(resp.
$a$
(resp.
![]() $b$
) be the smallest (resp. largest) slope of
$b$
) be the smallest (resp. largest) slope of
![]() $\unicode[STIX]{x1D709}^{\prime }$
.
$\unicode[STIX]{x1D709}^{\prime }$
.
In order to apply Theorem 4.2 to
![]() ${\mathcal{X}}$
, we need to choose
${\mathcal{X}}$
, we need to choose
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
as in Theorem 4.2. We define them as the union of three kinds of subsets of
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
as in Theorem 4.2. We define them as the union of three kinds of subsets of
![]() $\unicode[STIX]{x1D6EC}_{1}$
, which are labeled as
$\unicode[STIX]{x1D6EC}_{1}$
, which are labeled as
![]() $A,B$
and
$A,B$
and
![]() $C$
. (For the definition of
$C$
. (For the definition of
![]() $\unicode[STIX]{x1D6EC}_{1}$
, see the sentence following (8) in §3. Recall that
$\unicode[STIX]{x1D6EC}_{1}$
, see the sentence following (8) in §3. Recall that
![]() $\unicode[STIX]{x1D6EC}_{1}$
is canonically identified with the set of slopes
$\unicode[STIX]{x1D6EC}_{1}$
is canonically identified with the set of slopes
![]() $\unicode[STIX]{x1D706}\in \mathbb{Q}$
with
$\unicode[STIX]{x1D706}\in \mathbb{Q}$
with
![]() $0\leqslant \unicode[STIX]{x1D706}\leqslant 1$
.) First,
$0\leqslant \unicode[STIX]{x1D706}\leqslant 1$
.) First,
![]() $A$
is the set of slopes of
$A$
is the set of slopes of
![]() $\unicode[STIX]{x1D701}$
. Let
$\unicode[STIX]{x1D701}$
. Let
![]() $B$
be the set of
$B$
be the set of
![]() $\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}_{1}$
such that
$\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}_{1}$
such that
![]() $v_{\unicode[STIX]{x1D708}}$
or
$v_{\unicode[STIX]{x1D708}}$
or
![]() $-v_{\unicode[STIX]{x1D708}}$
is equal to
$-v_{\unicode[STIX]{x1D708}}$
is equal to
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
for some slope
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
for some slope
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $\unicode[STIX]{x1D701}^{\prime }$
. For each positive slope
$\unicode[STIX]{x1D701}^{\prime }$
. For each positive slope
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $\unicode[STIX]{x1D70C}$
, we choose a
$\unicode[STIX]{x1D70C}$
, we choose a
![]() $\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}_{1}$
satisfying the following two properties: (i)
$\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}_{1}$
satisfying the following two properties: (i)
![]() $\langle v_{\unicode[STIX]{x1D708}},v_{\unicode[STIX]{x1D706}}\rangle =1$
and (ii)
$\langle v_{\unicode[STIX]{x1D708}},v_{\unicode[STIX]{x1D706}}\rangle =1$
and (ii)
![]() $\overline{\unicode[STIX]{x1D708}}$
is sufficiently close to
$\overline{\unicode[STIX]{x1D708}}$
is sufficiently close to
![]() $\unicode[STIX]{x1D706}$
so that
$\unicode[STIX]{x1D706}$
so that
![]() $\overline{\unicode[STIX]{x1D708}}$
is distinct from the slope of any element of
$\overline{\unicode[STIX]{x1D708}}$
is distinct from the slope of any element of
![]() $A\cup B$
. Let
$A\cup B$
. Let
![]() $C$
be the set of such
$C$
be the set of such
![]() $\unicode[STIX]{x1D708}$
s. Let
$\unicode[STIX]{x1D708}$
s. Let
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
be the union of
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
be the union of
![]() $A,B$
and
$A,B$
and
![]() $C$
, and arrange them so that
$C$
, and arrange them so that
![]() $\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. Theorem 4.2 is applicable for these
$\overline{\unicode[STIX]{x1D707}_{1}}>\cdots >\overline{\unicode[STIX]{x1D707}_{\ell }}$
. Theorem 4.2 is applicable for these
![]() $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
. Indeed,
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell }$
. Indeed,
holds for
![]() $i=1,\ldots ,\ell$
. For
$i=1,\ldots ,\ell$
. For
![]() $\unicode[STIX]{x1D707}_{i}\in A$
, this follows from the fact that
$\unicode[STIX]{x1D707}_{i}\in A$
, this follows from the fact that
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is quasi-saturated (Lemma 2.2). For
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is quasi-saturated (Lemma 2.2). For
![]() $\unicode[STIX]{x1D707}_{i}\in B$
, the slope of
$\unicode[STIX]{x1D707}_{i}\in B$
, the slope of
![]() $\unicode[STIX]{x1D707}_{i}$
is outside
$\unicode[STIX]{x1D707}_{i}$
is outside
![]() $[a,b]$
; hence, the left-hand side of (26) is equal to zero. Moreover, for
$[a,b]$
; hence, the left-hand side of (26) is equal to zero. Moreover, for
![]() $\unicode[STIX]{x1D707}_{i}\in C$
, the inequality (26) holds.
$\unicode[STIX]{x1D707}_{i}\in C$
, the inequality (26) holds.
Let
![]() ${\mathcal{Y}}$
be the
${\mathcal{Y}}$
be the
![]() $p$
-divisible group obtained by Theorem 4.2. Let
$p$
-divisible group obtained by Theorem 4.2. Let
![]() $s$
be any geometric point of
$s$
be any geometric point of
![]() $\unicode[STIX]{x1D70B}^{-1}(D)$
. Let
$\unicode[STIX]{x1D70B}^{-1}(D)$
. Let
![]() $\unicode[STIX]{x1D706}$
be any slope of
$\unicode[STIX]{x1D706}$
be any slope of
![]() $\unicode[STIX]{x1D701}$
. Let
$\unicode[STIX]{x1D701}$
. Let
![]() $Z_{\unicode[STIX]{x1D706}}$
be the nonzero
$Z_{\unicode[STIX]{x1D706}}$
be the nonzero
![]() $\operatorname{Gr}_{i}({\mathcal{Y}}_{s})$
of slope
$\operatorname{Gr}_{i}({\mathcal{Y}}_{s})$
of slope
![]() $\unicode[STIX]{x1D706}$
. Since
$\unicode[STIX]{x1D706}$
. Since
![]() ${\mathcal{Y}}_{s}$
is completely slope divisible,
${\mathcal{Y}}_{s}$
is completely slope divisible,
![]() $Z_{\unicode[STIX]{x1D706}}$
is slope divisible with respect to
$Z_{\unicode[STIX]{x1D706}}$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D706}$
. If
$\unicode[STIX]{x1D706}$
. If
![]() $\unicode[STIX]{x1D706}$
is zero, then
$\unicode[STIX]{x1D706}$
is zero, then
![]() $Z_{\unicode[STIX]{x1D706}}$
is étale and therefore
$Z_{\unicode[STIX]{x1D706}}$
is étale and therefore
![]() $Z_{\unicode[STIX]{x1D706}}\simeq H_{1,0}$
, whence this is minimal. If
$Z_{\unicode[STIX]{x1D706}}\simeq H_{1,0}$
, whence this is minimal. If
![]() $\unicode[STIX]{x1D706}>0$
, then there exists
$\unicode[STIX]{x1D706}>0$
, then there exists
![]() $\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell },\unicode[STIX]{x1D707}_{1}^{\ast },\ldots ,\unicode[STIX]{x1D707}_{\ell }^{\ast }\}$
such that
$\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{\ell },\unicode[STIX]{x1D707}_{1}^{\ast },\ldots ,\unicode[STIX]{x1D707}_{\ell }^{\ast }\}$
such that
![]() $\langle v_{\unicode[STIX]{x1D708}},v_{\unicode[STIX]{x1D706}}\rangle =1$
, and
$\langle v_{\unicode[STIX]{x1D708}},v_{\unicode[STIX]{x1D706}}\rangle =1$
, and
![]() $Z_{\unicode[STIX]{x1D706}}$
is slope divisible with respect to
$Z_{\unicode[STIX]{x1D706}}$
is slope divisible with respect to
![]() $\unicode[STIX]{x1D708}$
. It follows from Proposition 3.12 that
$\unicode[STIX]{x1D708}$
. It follows from Proposition 3.12 that
![]() $Z_{\unicode[STIX]{x1D706}}$
is minimal. Thus, every
$Z_{\unicode[STIX]{x1D706}}$
is minimal. Thus, every
![]() $\operatorname{Gr}_{i}({\mathcal{Y}}_{s})$
is minimal, and therefore so is
$\operatorname{Gr}_{i}({\mathcal{Y}}_{s})$
is minimal, and therefore so is
![]() ${\mathcal{Y}}_{s}$
.◻
${\mathcal{Y}}_{s}$
.◻
Example 4.4. For the case of Example 2.3, we illustrate the subsets
![]() $A$
,
$A$
,
![]() $B$
and
$B$
and
![]() $C$
of
$C$
of
![]() $\unicode[STIX]{x1D6EC}_{1}$
that appear in the proof of Corollary 4.3. The saturated pair of Newton polygons is
$\unicode[STIX]{x1D6EC}_{1}$
that appear in the proof of Corollary 4.3. The saturated pair of Newton polygons is
![]() $\unicode[STIX]{x1D709}=(0,1)+_{\operatorname{NP}}(1,3)+_{\operatorname{NP}}(3,1)+_{\operatorname{NP}}(1,0)$
and
$\unicode[STIX]{x1D709}=(0,1)+_{\operatorname{NP}}(1,3)+_{\operatorname{NP}}(3,1)+_{\operatorname{NP}}(1,0)$
and
![]() $\unicode[STIX]{x1D701}=(0,1)+_{\operatorname{NP}}(1,2)+_{\operatorname{NP}}(1,1)+_{\operatorname{NP}}(2,1)+_{\operatorname{NP}}(1,0)$
. We use the identification of
$\unicode[STIX]{x1D701}=(0,1)+_{\operatorname{NP}}(1,2)+_{\operatorname{NP}}(1,1)+_{\operatorname{NP}}(2,1)+_{\operatorname{NP}}(1,0)$
. We use the identification of
![]() $\unicode[STIX]{x1D6EC}_{1}$
with the set of slopes. First, as
$\unicode[STIX]{x1D6EC}_{1}$
with the set of slopes. First, as
![]() $A$
is the set of slopes of
$A$
is the set of slopes of
![]() $\unicode[STIX]{x1D701}$
, we have
$\unicode[STIX]{x1D701}$
, we have
![]() $A=\{1,2/3,1/2,1/3,0\}$
. In Figure 3, the dotted arrows correspond to the elements of
$A=\{1,2/3,1/2,1/3,0\}$
. In Figure 3, the dotted arrows correspond to the elements of
![]() $B$
. Therefore,
$B$
. Therefore,
![]() $B=\{1,3/4,0\}$
.
$B=\{1,3/4,0\}$
.

Figure 3. The picture of
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
.
Finally,
![]() $n/(n+1)$
for any sufficiently large
$n/(n+1)$
for any sufficiently large
![]() $n$
can be an element of
$n$
can be an element of
![]() $C$
. If we choose
$C$
. If we choose
![]() $4/5$
, then
$4/5$
, then
![]() $C=\{4/5\}$
. Thus, the union of
$C=\{4/5\}$
. Thus, the union of
![]() $A$
,
$A$
,
![]() $B$
and
$B$
and
![]() $C$
is
$C$
is
5 Application: the configuration of minimal
 $p$
-kernel types
$p$
-kernel types
Recall from [Reference Harashita2, Corollary 3.2] that the central streams [Reference Oort11, 3.10] in the moduli space of principally polarized abelian varieties are configurated as given by the partial ordering on symmetric Newton polygons. As an application of Corollary 1.1, we show its unpolarized analog (Corollary 5.1) with a geometrical proof, whereas a combinatorial method is used in [Reference Harashita2].
Let
![]() $h$
be a natural number. Let
$h$
be a natural number. Let
![]() $c,d$
be nonnegative integers, with
$c,d$
be nonnegative integers, with
![]() $c+d=h$
. Let
$c+d=h$
. Let
![]() $W$
be the Weyl group of
$W$
be the Weyl group of
![]() $\operatorname{GL}_{h}$
. Let
$\operatorname{GL}_{h}$
. Let
![]() $\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{h-1}\}$
be the set of simple roots, as usual. Let
$\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{h-1}\}$
be the set of simple roots, as usual. Let
![]() $s_{i}$
be the simple reflection associated to
$s_{i}$
be the simple reflection associated to
![]() $\unicode[STIX]{x1D6FC}_{i}$
. Set
$\unicode[STIX]{x1D6FC}_{i}$
. Set
![]() $I=\unicode[STIX]{x1D6E5}\setminus \{\unicode[STIX]{x1D6FC}_{c}\}$
. Let
$I=\unicode[STIX]{x1D6E5}\setminus \{\unicode[STIX]{x1D6FC}_{c}\}$
. Let
![]() $W_{I}$
be the subgroup of
$W_{I}$
be the subgroup of
![]() $W$
generated by
$W$
generated by
![]() $s_{i}$
with
$s_{i}$
with
![]() $\unicode[STIX]{x1D6FC}_{i}\in I$
. Let
$\unicode[STIX]{x1D6FC}_{i}\in I$
. Let
![]() $^{I}W$
be the set of the minimal-length representatives of
$^{I}W$
be the set of the minimal-length representatives of
![]() $W_{I}\backslash W$
.
$W_{I}\backslash W$
.
Let
![]() $k$
be an algebraically closed field. Recall the classification theory of truncated Barsotti–Tate groups of level one (
$k$
be an algebraically closed field. Recall the classification theory of truncated Barsotti–Tate groups of level one (
![]() $\operatorname{BT}_{1}$
s) over
$\operatorname{BT}_{1}$
s) over
![]() $k$
found by Kraft [Reference Kraft8], rediscovered by Oort and reproved and formulated as follows by Moonen and Wedhorn [Reference Moonen and Wedhorn9]. It says that there exists a canonical bijection from
$k$
found by Kraft [Reference Kraft8], rediscovered by Oort and reproved and formulated as follows by Moonen and Wedhorn [Reference Moonen and Wedhorn9]. It says that there exists a canonical bijection from
![]() $^{I}W$
to the set of isomorphism classes of
$^{I}W$
to the set of isomorphism classes of
![]() $\operatorname{BT}_{1}$
s over
$\operatorname{BT}_{1}$
s over
![]() $k$
of codimension
$k$
of codimension
![]() $c$
and of dimension
$c$
and of dimension
![]() $d$
.
$d$
.
We use
![]() $F$
-zips, which in this paper mean those with support contained in
$F$
-zips, which in this paper mean those with support contained in
![]() $\{0,1\}$
in the terminology of [Reference Moonen and Wedhorn9]. Let
$\{0,1\}$
in the terminology of [Reference Moonen and Wedhorn9]. Let
![]() $S$
be a scheme in characteristic
$S$
be a scheme in characteristic
![]() $p>0$
. An
$p>0$
. An
![]() $F$
-zip over
$F$
-zip over
![]() $S$
is a quintuple
$S$
is a quintuple
![]() $(N,C,D,\unicode[STIX]{x1D711},\dot{\unicode[STIX]{x1D711}})$
consisting of a locally free
$(N,C,D,\unicode[STIX]{x1D711},\dot{\unicode[STIX]{x1D711}})$
consisting of a locally free
![]() ${\mathcal{O}}_{S}$
-module
${\mathcal{O}}_{S}$
-module
![]() $N$
and
$N$
and
![]() ${\mathcal{O}}_{S}$
-submodules
${\mathcal{O}}_{S}$
-submodules
![]() $C,D$
of
$C,D$
of
![]() $N$
which are locally direct summands of
$N$
which are locally direct summands of
![]() $N$
with
$N$
with
![]() ${\mathcal{O}}_{S}$
-linear isomorphisms
${\mathcal{O}}_{S}$
-linear isomorphisms
![]() $\unicode[STIX]{x1D711}:(N/C)^{(p)}\rightarrow D$
and
$\unicode[STIX]{x1D711}:(N/C)^{(p)}\rightarrow D$
and
![]() $\dot{\unicode[STIX]{x1D711}}:C^{(p)}\rightarrow N/D$
. Let
$\dot{\unicode[STIX]{x1D711}}:C^{(p)}\rightarrow N/D$
. Let
![]() $G$
be a
$G$
be a
![]() $\operatorname{BT}_{1}$
over
$\operatorname{BT}_{1}$
over
![]() $k$
. To
$k$
. To
![]() $G$
, we associate an
$G$
, we associate an
![]() $F$
-zip
$F$
-zip
![]() $(\mathbb{D}(G),V\mathbb{D}(G),F\mathbb{D}(G),F,V^{-1})$
. This gives a canonical bijection from the set of
$(\mathbb{D}(G),V\mathbb{D}(G),F\mathbb{D}(G),F,V^{-1})$
. This gives a canonical bijection from the set of
![]() $\operatorname{BT}_{1}$
s over
$\operatorname{BT}_{1}$
s over
![]() $k$
and the set of
$k$
and the set of
![]() $F$
-zips over
$F$
-zips over
![]() $k$
.
$k$
.
Let
![]() $w_{\unicode[STIX]{x1D709}}\in ^{I}W$
denote the
$w_{\unicode[STIX]{x1D709}}\in ^{I}W$
denote the
![]() $p$
-kernel type of the minimal
$p$
-kernel type of the minimal
![]() $p$
-divisible group
$p$
-divisible group
![]() $H(\unicode[STIX]{x1D709})_{k}$
of the Newton polygon
$H(\unicode[STIX]{x1D709})_{k}$
of the Newton polygon
![]() $\unicode[STIX]{x1D709}$
. For
$\unicode[STIX]{x1D709}$
. For
![]() $v,w\in ^{I}W$
, we say that
$v,w\in ^{I}W$
, we say that
![]() $v\subset w$
if there exists an
$v\subset w$
if there exists an
![]() $F$
-zip over a discrete valuation ring of which the generic fiber (resp. the special fiber) is of type
$F$
-zip over a discrete valuation ring of which the generic fiber (resp. the special fiber) is of type
![]() $w$
(resp. of type
$w$
(resp. of type
![]() $v$
). It follows from [Reference Pink, Ziegler and Wedhorn14, Theorem 12.17] that
$v$
). It follows from [Reference Pink, Ziegler and Wedhorn14, Theorem 12.17] that
![]() $\subset$
is a partial ordering on
$\subset$
is a partial ordering on
![]() $^{I}W$
, and this coincides with the partial ordering introduced and investigated by He [Reference He5].
$^{I}W$
, and this coincides with the partial ordering introduced and investigated by He [Reference He5].
Corollary 5.1.
![]() $w_{\unicode[STIX]{x1D701}}\subset w_{\unicode[STIX]{x1D709}}$
if and only if
$w_{\unicode[STIX]{x1D701}}\subset w_{\unicode[STIX]{x1D709}}$
if and only if
![]() $\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
.
Proof. For the if part, since
![]() $\subset$
is a partial ordering, it is sufficient to show the case that
$\subset$
is a partial ordering, it is sufficient to show the case that
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is saturated. Applying Corollary 1.1 to a family with saturated
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
is saturated. Applying Corollary 1.1 to a family with saturated
![]() $\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
and with
$\unicode[STIX]{x1D701}\prec \unicode[STIX]{x1D709}$
and with
![]() $a$
-number
$a$
-number
![]() ${\leqslant}1$
, constructed in [Reference Oort10, (3.2)], we have
${\leqslant}1$
, constructed in [Reference Oort10, (3.2)], we have
![]() $w_{\unicode[STIX]{x1D701}}\subset w_{\unicode[STIX]{x1D709}}$
.
$w_{\unicode[STIX]{x1D701}}\subset w_{\unicode[STIX]{x1D709}}$
.
Suppose that
![]() $w_{\unicode[STIX]{x1D701}}\subset w_{\unicode[STIX]{x1D709}}$
. There exists an
$w_{\unicode[STIX]{x1D701}}\subset w_{\unicode[STIX]{x1D709}}$
. There exists an
![]() $F$
-zip
$F$
-zip
![]() ${\mathcal{N}}$
over a discrete valuation ring
${\mathcal{N}}$
over a discrete valuation ring
![]() $R$
with algebraically closed residue field whose special fiber is of type
$R$
with algebraically closed residue field whose special fiber is of type
![]() $w_{\unicode[STIX]{x1D701}}$
and whose generic fiber is of type
$w_{\unicode[STIX]{x1D701}}$
and whose generic fiber is of type
![]() $w_{\unicode[STIX]{x1D709}}$
. Then, there exists a display
$w_{\unicode[STIX]{x1D709}}$
. Then, there exists a display
![]() ${\mathcal{M}}$
over
${\mathcal{M}}$
over
![]() $R$
such that
$R$
such that
![]() ${\mathcal{M}}/I_{R}{\mathcal{M}}$
is isomorphic to
${\mathcal{M}}/I_{R}{\mathcal{M}}$
is isomorphic to
![]() ${\mathcal{N}}$
(see [Reference Harashita4, Lemma 4.1]). By [Reference Oort12], the special fiber (resp. the generic fiber) of
${\mathcal{N}}$
(see [Reference Harashita4, Lemma 4.1]). By [Reference Oort12], the special fiber (resp. the generic fiber) of
![]() ${\mathcal{M}}$
is minimal of Newton polygon
${\mathcal{M}}$
is minimal of Newton polygon
![]() $\unicode[STIX]{x1D701}$
(resp.
$\unicode[STIX]{x1D701}$
(resp.
![]() $\unicode[STIX]{x1D709}$
). By Grothendieck–Katz [Reference Katz7, Theorem 2.3.1 on p. 143], we have
$\unicode[STIX]{x1D709}$
). By Grothendieck–Katz [Reference Katz7, Theorem 2.3.1 on p. 143], we have
![]() $\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
.◻
$\unicode[STIX]{x1D701}\preccurlyeq \unicode[STIX]{x1D709}$
.◻
Combining this with [Reference Harashita4, Theorem 1.1], one can get the unpolarized analog of Oort’s conjecture [Reference Oort11, 6.9]. The original conjecture was proved in [Reference Harashita3, Reference Viehmann17] (see also [Reference Viehmann and Wedhorn18] for a generalization to some Shimura varieties).
Corollary 5.2. If there exists a
![]() $p$
-divisible group with Newton polygon
$p$
-divisible group with Newton polygon
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $p$
-kernel type
$p$
-kernel type
![]() $w$
, then we have
$w$
, then we have
![]() $w_{\unicode[STIX]{x1D709}}\subset w$
.
$w_{\unicode[STIX]{x1D709}}\subset w$
.
Proof. Let
![]() $\unicode[STIX]{x1D709}(w)$
be the supremum of Newton polygons of
$\unicode[STIX]{x1D709}(w)$
be the supremum of Newton polygons of
![]() $p$
-divisible groups with
$p$
-divisible groups with
![]() $p$
-kernel type
$p$
-kernel type
![]() $w$
. We have
$w$
. We have
![]() $\unicode[STIX]{x1D709}\preccurlyeq \unicode[STIX]{x1D709}(w)$
. From Corollary 5.1, it follows that
$\unicode[STIX]{x1D709}\preccurlyeq \unicode[STIX]{x1D709}(w)$
. From Corollary 5.1, it follows that
![]() $w_{\unicode[STIX]{x1D709}}\subset w_{\unicode[STIX]{x1D709}(w)}$
. Recall [Reference Harashita4, Theorem 1.1], which says that
$w_{\unicode[STIX]{x1D709}}\subset w_{\unicode[STIX]{x1D709}(w)}$
. Recall [Reference Harashita4, Theorem 1.1], which says that
![]() $\unicode[STIX]{x1D709}(w)$
is the maximal one among Newton polygons
$\unicode[STIX]{x1D709}(w)$
is the maximal one among Newton polygons
![]() $\unicode[STIX]{x1D702}$
with
$\unicode[STIX]{x1D702}$
with
![]() $w_{\unicode[STIX]{x1D702}}\subset w$
. In particular, we have
$w_{\unicode[STIX]{x1D702}}\subset w$
. In particular, we have
![]() $w_{\unicode[STIX]{x1D709}(w)}\subset w$
.◻
$w_{\unicode[STIX]{x1D709}(w)}\subset w$
.◻
Acknowledgments
I would like to thank Professor Frans Oort for nice discussions on some topics related to flat extensions and for helpful comments on this paper. The author thanks the referee for careful reading and helpful suggestions.