Refine listing
Actions for selected content:
145 results in 14Lxx
Arithmetically defined dense subgroups of Morava stabilizer groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 247-270
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
On lattices in semi-stable representations: a proof of a conjecture of Breuil
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 61-88
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
Monothetic algebraic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 315-324
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
THE SPECTRA OF THE SPHERICAL AND EUCLIDEAN TRIANGLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2007, pp. 217-227
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Involutions and commutators in orthogonal groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-36
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
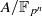 of dimension
of dimension 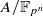 of
of 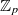 -lattices in semi-stable
-lattices in semi-stable 