Article contents
Arithmetically defined dense subgroups of Morava stabilizer groups
Published online by Cambridge University Press: 01 January 2008
Abstract
For every prime p and integer n≥3 we explicitly construct an abelian variety 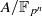 of dimension n such that for a suitable prime l the group of quasi-isogenies of
of dimension n such that for a suitable prime l the group of quasi-isogenies of 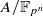 of l-power degree is canonically a dense subgroup of the nth Morava stabilizer group at p. We also give a variant of this result taking into account a polarization. This is motivated by the recent construction by Behrens and Lawson of topological automorphic forms which generalizes topological modular forms. For this, we prove some arithmetic results of independent interest: a result about approximation of local units in maximal orders of global skew fields which also gives a precise solution to the problem of extending automorphisms of the p-divisible group of a simple abelian variety over a finite field to quasi-isogenies of the abelian variety of degree divisible by as few primes as possible.
of l-power degree is canonically a dense subgroup of the nth Morava stabilizer group at p. We also give a variant of this result taking into account a polarization. This is motivated by the recent construction by Behrens and Lawson of topological automorphic forms which generalizes topological modular forms. For this, we prove some arithmetic results of independent interest: a result about approximation of local units in maximal orders of global skew fields which also gives a precise solution to the problem of extending automorphisms of the p-divisible group of a simple abelian variety over a finite field to quasi-isogenies of the abelian variety of degree divisible by as few primes as possible.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Foundation Compositio Mathematica 2008
- 3
- Cited by

