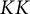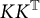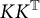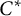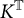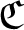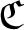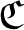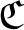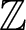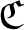Refine search
Actions for selected content:
99 results
MORPHISMS OF CUNTZ–PIMSNER ALGEBRAS FROM COMPLETELY POSITIVE MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 31 October 2025, pp. 1-40
-
- Article
- Export citation
COACTIONS OF COMPACT GROUPS ON Mn
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 31 October 2025, pp. 1-18
-
- Article
- Export citation
DEFORMATION OF FELL BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 31 October 2025, pp. 1-35
-
- Article
- Export citation
Simplicity of crossed products by FC-hypercentral groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 28 October 2025, pp. 2272-2319
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON TOEPLITZ ALGEBRAS OF PRODUCT SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SIMPLE TRACIALLY
 $\mathcal {Z}$-ABSORBING C*-ALGEBRAS
$\mathcal {Z}$-ABSORBING C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. 2135-2179
- Print publication:
- November 2025
-
- Article
- Export citation
Non-commutative skew-product extension dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2672-2694
- Print publication:
- September 2025
-
- Article
- Export citation
RELATIVE POSITION BETWEEN A PAIR OF SPIN MODEL SUBFACTORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-38
- Print publication:
- August 2025
-
- Article
- Export citation
KK-theory of circle actions with the Rokhlin property
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The imprimitivity Fell bundle
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-44
-
- Article
- Export citation
Realizations of free actions via their fixed point algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 17 January 2025, pp. 568-581
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
$C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 366-379
- Print publication:
- October 2025
-
- Article
- Export citation
On multiparameter CAR (canonical anticommutation relation) flows
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-37
-
- Article
- Export citation
Strongly outer actions of certain torsion-free amenable groups on the Razak–Jacelon algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coactions and skew products for topological quivers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 921-946
-
- Article
- Export citation
DYNAMICAL MCDUFF-TYPE PROPERTIES FOR GROUP ACTIONS ON VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 2593-2629
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of anomalous actions through model action absorption
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 916-939
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Actions of discrete amenable groups into the normalizers of full groups of ergodic transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 February 2024, pp. 3290-3315
- Print publication:
- November 2024
-
- Article
- Export citation
THE RIEFFEL CORRESPONDENCE FOR EQUIVALENT FELL BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 288-307
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dynamical classification for crossed products of fiberwise essentially minimal zero-dimensional dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2229-2256
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation