Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-27T13:44:40.564Z Has data issue: false hasContentIssue false
  • English
  • Français

SIMPLE TRACIALLY 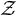$\mathcal {Z}$-ABSORBING C*-ALGEBRAS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  04 June 2025

Massoud Amini ,
Nasser Golestani Open the ORCID record for Nasser Golestani [Opens in a new window] ,
Saeid Jamali  and
N. Christopher Phillips
Massoud Amini
Affiliation:
Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran 14115-134
Nasser Golestani*
Affiliation:
Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran 14115-134
Saeid Jamali
Affiliation:
Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran 14115-134
N. Christopher Phillips
Affiliation:
Department of Mathematics, University of Oregon, Eugene OR 97403-1222
*
(n.golestani@modares.ac.ir)
Get access Rights & Permissions [Opens in a new window]

Abstract

We define a notion of tracial $\mathcal {Z}$-absorption for simple not necessarily unital C*-algebras, study it systematically and prove its permanence properties. This extends the notion defined by Hirshberg and Orovitz for unital C*-algebras. The Razak-Jacelon algebra, simple nonelementary C*-algebras with tracial rank zero, and simple purely infinite C*-algebras are tracially 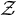$\mathcal {Z}$-absorbing. We obtain the first purely infinite examples of tracially 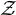$\mathcal {Z}$-absorbing C*-algebras which are not 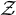$\mathcal {Z}$-absorbing. We use techniques from reduced free products of von Neumann algebras to construct these examples. A stably finite example was given by Z. Niu and Q. Wang in 2021. We study the Cuntz semigroup of a simple tracially 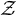$\mathcal {Z}$-absorbing C*-algebra and prove that it is almost unperforated and the algebra is weakly almost divisible.

Keywords

tracial 𝒵-absorption𝒵-absorptionCuntz semigrouppurely infinite C*-algebraCuntz subequivalence

MSC classification

Primary: 46L55: Noncommutative dynamical systems 46L80: $K$-theory and operator algebras (including cyclic theory)

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 24 , Issue 6 , November 2025 , pp. 2135 - 2179
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Amini, M, Golestani, N, Jamali, S and Phillips, NC (2024) Finite group and integer actions on simple tracially $\mathcal {Z}$ -absorbing C*-algebras. J. Operator Th. 92, 505–547.CrossRefGoogle Scholar
Ara, P, Perera, F and Toms, AS (2011) K-theory for operator algebras. Classification of C*-algebras. In Ara, P, Lledó, F and Perera, F (eds), Aspects of Operator Algebras and Applications, vol. 534. Contemporary Mathematics. Providence RI: American Mathematical Society, 1–71.CrossRefGoogle Scholar
Archey, D, Buck, J and Phillips, NC (2017) Centrally large subalgebras and tracial $\mathcal {Z}$ -absorption. Int. Math. Res. Not. 292, 1–21.Google Scholar
Archey, D and Phillips, NC (2020) Permanence of stable rank one for centrally large subalgebras and crossed products by minimal homeomorphisms. J. Operator Th. 83, 353–389.CrossRefGoogle Scholar
Avitzour, D (1982) Free products of C*-algebras. Trans. Amer. Math. Soc. 271, 423–435.Google Scholar
Blackadar, B (1978) Weak expectations and nuclear C*-algebras. Indiana Univ. Math. J. 27, 1021–1026.CrossRefGoogle Scholar
Blackadar, B (2006) Operator algebras. Theory of C*-Algebras and von Neumann Algebras , vol. 122. Encyclopaedia of Mathematical Sciences, Operator Algebras and Non-commutative Geometry, III. Berlin: Springer-Verlag.Google Scholar
Blackadar, B and Handelman, D (1982) Dimension functions and traces on C*-algebras. J. Funct. Anal. 45, 297–340.CrossRefGoogle Scholar
Blackadar, B, Robert, L, Tikuisis, AP, Toms, AS and Winter, W (2002) An algebraic approach to the radius of comparison. Trans. Amer. Math. Soc. 364, 3657–3674.CrossRefGoogle Scholar
Barnett, L (1995) Free product von Neumann algebras of type $\mathrm{III}$ . Proc. Amer. Math. Soc. 123, 543–553.Google Scholar
Castillejos, J and Evington, S (2020) Nuclear dimension of stably projectionless C*-algebras. Anal. PDE. 13(7), 2205–2240.CrossRefGoogle Scholar
Castillejos, J, Evington, S, Tikuisis, A, White, S and Winter, W (2020) Nuclear dimension of simple C*-algebras, Invent. Math. https://doi.org/10.1007/s00222-020-01013-1.Google Scholar
Castillejos, J, Evington, S, Tikuisis, A and White, S, Uniform, Property $\Gamma$ . To appear in Int . Math. Res. Not. https://doi.org/10.1093/imrn/rnaa282.Google Scholar
Castillejos, J, Li, K and Szabó, G (2023) On tracial -stability of simple non-unital C*-algebras, Canad. J. Math. 1–20. doi:10.4153/S0008414X23000202.CrossRefGoogle Scholar
Cuntz, J (1981) K-theory for certain C*-algebras. Ann. Math. 113, 181–197.CrossRefGoogle Scholar
Dykema, KJ (2002) Purely infinite, simple C*-algebras arising from free product constructions, II. Math. Scand. 90, 73–86.CrossRefGoogle Scholar
Dykema, KJ and Rørdam, M (1998) Purely infinite simple C*-algebras arising from free product constructions. Canad. J. Math. 50, 323–341.CrossRefGoogle Scholar
Elliott, GA, Gong, G, Lin, H and Niu, Z (2020) Simple stably projectionless C*-algebras with generalized tracial rank one. J. Noncommut. Geom. 14, 251–347.CrossRefGoogle Scholar
Elliott, GA, Robert, L and Santiago, L (2011) The cone of lower semicontinuous traces on a C*-algebra. Amer. J. Math. 133, 969–1005.CrossRefGoogle Scholar
Forough, M and Golestani, N (2017) Tracial Rokhlin property for finite group actions on non-unital simple C*-algebras. arXiv preprint 1711.10818v1 [math.OA].Google Scholar
Forough, M and Golestani, N (2020) The weak tracial Rokhlin property for finite group actions on simple C*-algebras. Doc. Math. 25, 2507–2552.CrossRefGoogle Scholar
Fu, X, Li, K and Lin, H (2022) Tracial approximate divisibility and stable rank one. J. Lond. Math. Soc. 106, 3008–3042.CrossRefGoogle Scholar
Fu, X and Lin, H (2022) Non-amenable simple C*-algebras with tracial approximation. Forum of Mathematics, Sigma 10, 1–50.CrossRefGoogle Scholar
Gardella, E and Hirshberg, I (2020) Strongly outer actions of amenable groups on $\mathcal {Z}$ -stable C*-algebras. arXiv preprint 1811.00447v3 [math.OA].Google Scholar
Gong, G and Lin, H (2017) On classification of non-unital simple amenable C*-algebras, I. arXiv preprint 1611.04440v3 [math.OA].Google Scholar
Gong, G and Lin, H (2020) On classification of non-unital simple amenable C*-algebras, II. J. Geom. Phys. 158, 1–102.CrossRefGoogle Scholar
Gong, G and Lin, H (2022) On classification of non-unital amenable simple C*-algebras, III, stably projectionless C*-algebras. Ann. K-Theory 7, 279–384.CrossRefGoogle Scholar
Hirshberg, I and Orovitz, J (2013) Tracially $\mathcal {Z}$ -absorbing C*-algebras. J. Funct. Anal. 265, 765–785.CrossRefGoogle Scholar
Jacelon, B (2013) A simple, monotracial, stably projectionless C*-algebra. J. London Math. Soc. (2) 87, 365–383.CrossRefGoogle Scholar
Jamali, S (2018) Simple Tracially $\mathcal {Z}$ -Absorbing C*-Algebras. PhD thesis (Persian), Tarbiat Modares University.Google Scholar
Jiang, X and Su, H (1999) On a simple unital projectionless C*-algebra. Amer. J. Math. 121, 359–413.CrossRefGoogle Scholar
Kerr, D, Dimension, comparison, and almost finiteness. To appear in J . Eur. Math. Soc. https://doi.org/10.4171/JEMS/995.Google Scholar
Kirchberg, E and Rørdam, M (2000) Non-simple purely infinite C*-algebras. Amer. J. Math. 122, 637–666.CrossRefGoogle Scholar
Kirchberg, E and Rørdam, M (2002) Infinite non-simple C*-algebras: absorbing the Cuntz algebra ${\mathcal{O}}_{\infty }$ . Adv. Math. 167, 195–264.CrossRefGoogle Scholar
Kirchberg, E and Winter, W (2004) Covering dimension and quasidiagonality. Internat. J. Math. 15, 63–85.CrossRefGoogle Scholar
Lin, H (2001) The tracial topological rank of C*-algebras. Proc. London Math. Soc. (3) 83, 199–234.CrossRefGoogle Scholar
Lin, H (2001) Tracially AF C*-algebras. Trans. Amer. Math. Soc. 353, 693–722.CrossRefGoogle Scholar
Lin, H (2001) An Introduction to the Classification of Amenable C*-Algebras. River Edge NJ: World Scientific.Google Scholar
Lin, H and Niu, Z (2008) Lifting KK-elements, asymptotic unitary equivalence and classification of simple C*-algebras. Adv. Math. 219, 1729–1769.CrossRefGoogle Scholar
Matui, H and Sato, Y (2012) Strict comparison and -absorption of nuclear C*-algebras. Acta Math. 209, 179–196.CrossRefGoogle Scholar
Niu, Z and Wang, Q (2021) A tracially AF algebra which is not $\mathrm{Z}$ -stable. Münster J. of Math. 14, 41–57.Google Scholar
Nawata, N (2019) Trace scaling automorphisms of the stabilized Razak-Jacelon algebra, Proc. Lond. Math. Soc. (3) 118(3), 545–576.CrossRefGoogle Scholar
Orovitz, J, Phillips, NC and Wang, Q, Strict comparison and crossed products. In preparation.Google Scholar
Osaka, H and Phillips, NC (2006) Stable and real rank for crossed products by automorphisms with the tracial Rokhlin property. Ergod. Th. Dynam. Sys. 26, 1579–1621.CrossRefGoogle Scholar
Pedersen, GK (1979) C*-Algebras and Their Automorphism Groups. London, New York, San Francisco: Academic Press.Google Scholar
Phillips, NC (2014) Large subalgebras. arXiv preprint 1408.5546v1 [math.OA].Google Scholar
Raeburn, I and Williams, DP (1998) Morita Equivalence and Continuous-Trace C*-Algebras , no. 60. Mathematical Surveys and Monographs. Providence RI: American Mathematical Society.Google Scholar
Rørdam, M (1992) On the structure of simple C*-algebras tensored with a UHF-algebra, II. J. Funct. Anal. 107, 255–269.CrossRefGoogle Scholar
Rørdam, M (2002) Classification of nuclear, simple C*-algebras. In Rørdam, M and Størmer, E, Classification of Nuclear C*-algebras. Entropy in Operator Algebras, vol. 126. Encyclopaedia of Mathematical Sciences. Berlin: Springer-Verlag, 1–145.CrossRefGoogle Scholar
Rørdam, M (2004) The stable and the real rank of $\mathcal {Z}$ -absorbing C*-algebras. Internat. J. Math. 15, 1065–1084.CrossRefGoogle Scholar
Tikuisis, A (2014) Nuclear dimension, $Z$ -stability, and algebraic simplicity for stably projectionless C*-algebras. Math. Ann. 358, 729–778.CrossRefGoogle Scholar
Toms, AS and Winter, W (2007) Strongly self-absorbing C*-algebras. Trans. Amer. Math. Soc. 359, 3999–4029.CrossRefGoogle Scholar
Winter, W (2012) Nuclear dimension and $\mathcal {Z}$ -stability of pure C*-algebras. Invent. Math. 187, 259–342.CrossRefGoogle Scholar
Winter, W (2014) Localizing the Elliott conjecture at strongly self-absorbing C*-algebras. J. Reine Angew. Math. 692, 193–231.CrossRefGoogle Scholar
Winter, W and Zacharias, J (2009) Completely positive maps of order zero. Münster J. Math. 2, 311–324.Google Scholar