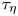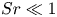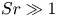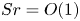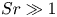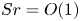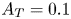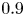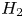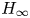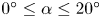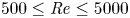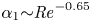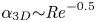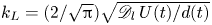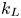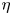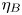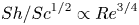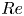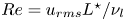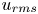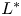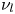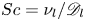Contents
JFM Papers
Mechanisms of mass transfer to small spheres sinking in turbulence
-
- Published online by Cambridge University Press:
- 03 January 2023, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bubble re-acceleration behaviours in compressible Rayleigh–Taylor instability with isothermal stratification
-
- Published online by Cambridge University Press:
- 03 January 2023, A16
-
- Article
- Export citation
Well-posedness and ill-posedness of single-phase models for suspensions
-
- Published online by Cambridge University Press:
- 03 January 2023, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Granular flows in drums of non-uniform widths
-
- Published online by Cambridge University Press:
- 03 January 2023, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear wave attenuation in strongly confined falling liquid films sheared by a laminar counter-current gas flow
-
- Published online by Cambridge University Press:
- 03 January 2023, A19
-
- Article
- Export citation
Reactive control of second Mack mode in a supersonic boundary layer with free-stream velocity/density variations
-
- Published online by Cambridge University Press:
- 05 January 2023, A20
-
- Article
- Export citation
Circular bubbles in a Hele-Shaw channel: a Hele-Shaw Newton's cradle
-
- Published online by Cambridge University Press:
- 03 January 2023, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibria and stabilities of a confined floating cylinder
-
- Published online by Cambridge University Press:
- 03 January 2023, A22
-
- Article
- Export citation
Energetics of buoyancy-generated turbulent flows with active scalar: pure buoyant plume
-
- Published online by Cambridge University Press:
- 03 January 2023, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reconstruction of the 3-D fields with a depth-averaged model for open-channel flows in the smooth turbulent case
-
- Published online by Cambridge University Press:
- 03 January 2023, A24
-
- Article
- Export citation
Second-order inertial forces and torques on a sphere in a viscous steady linear flow
-
- Published online by Cambridge University Press:
- 03 January 2023, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two- and three-dimensional wake transitions of a NACA0012 airfoil
-
- Published online by Cambridge University Press:
- 06 January 2023, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large eddy simulations of the accumulation of buoyant material in oceanic wind-driven and convective turbulence
-
- Published online by Cambridge University Press:
- 06 January 2023, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximate streamsurfaces for flow visualization
-
- Published online by Cambridge University Press:
- 09 January 2023, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direct numerical simulations of bubble-mediated gas transfer and dissolution in quiescent and turbulent flows
-
- Published online by Cambridge University Press:
- 06 January 2023, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The structure of energy fluxes in wave turbulence
-
- Published online by Cambridge University Press:
- 06 January 2023, A30
-
- Article
- Export citation
The stability of inviscid Beltrami flow between parallel free-slip impermeable boundaries
-
- Published online by Cambridge University Press:
- 09 January 2023, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hypersonic flow over spherically blunted cone capsules for atmospheric entry. Part 2. Vibrational non-equilibrium effects
-
- Published online by Cambridge University Press:
- 06 January 2023, A32
-
- Article
- Export citation
Experimental study of axial flow evolution and area-varying waves in concentrated vortices
-
- Published online by Cambridge University Press:
- 06 January 2023, A33
-
- Article
- Export citation
Aerodynamics and fluid–structure interaction of an airfoil with actively controlled flexible leeward surface
-
- Published online by Cambridge University Press:
- 06 January 2023, A34
-
- Article
- Export citation