Volume 1026 - 10 January 2026
Latest volume of Journal of Fluid Mechanics
Contents
Corrigendum
The joint effects of planetary
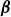 $\boldsymbol{\beta}$, topography and friction on baroclinic instability in a two-layer QG model – CORRIGENDUM
$\boldsymbol{\beta}$, topography and friction on baroclinic instability in a two-layer QG model – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 09 January 2026, E1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Capturing the motion of a pair of elastic capsules in a shear flow: emergent nonlinear hydrodynamic ordering
-
- Published online by Cambridge University Press:
- 09 January 2026, A50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Onset and length scales of wall modes in confined magnetoconvection with a vertical magnetic field
-
- Published online by Cambridge University Press:
- 07 January 2026, A41
-
- Article
- Export citation
Buckling of a floating fluid layer
-
- Published online by Cambridge University Press:
- 07 January 2026, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Passive drag reduction on a sphere using azimuthally spaced surface protrusions: effects of protrusion number at fixed coverage
-
- Published online by Cambridge University Press:
- 07 January 2026, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scaling for compression waves/boundary layer interaction based on equivalent interaction intensity
-
- Published online by Cambridge University Press:
- 07 January 2026, A40
-
- Article
- Export citation
Linear and nonlinear interactions between stationary cross-flow instabilities and a smooth surface hump
-
- Published online by Cambridge University Press:
- 06 January 2026, A43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dissolution-driven transport in a rotating horizontal cylinder
-
- Published online by Cambridge University Press:
- 07 January 2026, A39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the mechanism of dual tones in transitional flow around a heptagonal cylinder
-
- Published online by Cambridge University Press:
- 05 January 2026, A37
-
- Article
- Export citation
Enthalpy transformation for wall-bounded supercritical flows with heat transfer
-
- Published online by Cambridge University Press:
- 05 January 2026, A36
-
- Article
- Export citation
Influence of aspect ratio on the stability of rotating microchannel flows with superhydrophobic walls
-
- Published online by Cambridge University Press:
- 05 January 2026, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effects of spanwise streamline curvature on a spatially developing boundary layer
-
- Published online by Cambridge University Press:
- 05 January 2026, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mechanism generating reverse buoyancy flux at the small scales of stably stratified turbulence
-
- Published online by Cambridge University Press:
- 05 January 2026, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Model predictive control of fluid–structure interaction via Koopman-based reduced-order model
-
- Published online by Cambridge University Press:
- 05 January 2026, A32
-
- Article
- Export citation
On the interdependence between flame shape and vortex breakdown mode in turbulent swirling reacting flows
-
- Published online by Cambridge University Press:
- 05 January 2026, A34
-
- Article
- Export citation
Ocean transit times: from basin to planetary scales
-
- Published online by Cambridge University Press:
- 02 January 2026, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convective and inertial Marangoni surfing
-
- Published online by Cambridge University Press:
- 02 January 2026, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The mechanism of laminar boundary layer vortex shedding noise generation of jet–wing interaction under the wing-in-ground effect
-
- Published online by Cambridge University Press:
- 04 January 2026, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The action of spatial modulation of a transverse temperature gradient on floating droplets dynamics
-
- Published online by Cambridge University Press:
- 02 January 2026, A28
-
- Article
- Export citation
Role of acoustic metasurface in the nonlinear mode–mode interaction and breakdown of hypersonic boundary layer
-
- Published online by Cambridge University Press:
- 02 January 2026, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation