Article contents
The structure of energy fluxes in wave turbulence
Published online by Cambridge University Press: 06 January 2023
Abstract
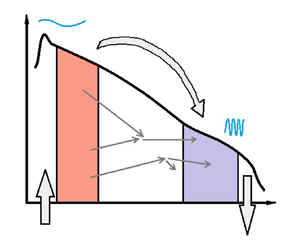
We calculate the net energy per unit time exchanged between two sets of modes in a generic system governed by a three-wave kinetic equation. Our calculation is based on the property of detailed energy conservation of the triadic resonant interactions. In a first application to isotropic systems, we re-derive the previously used formula for the energy flux as a particular case for adjacent sets. We then exploit the new formalism to quantify the level of locality of the energy transfers in the example of surface capillary waves. A second application to anisotropic wave systems expands the currently available set of tools to investigate magnitude and direction of the energy fluxes in these systems. We illustrate the use of the formalism by characterizing the energy pathways in the oceanic internal wavefield. Our proposed approach, unlike traditional approaches, is not limited to stationarity, scale invariance and strict locality. In addition, we define a number  $w$ that quantifies the scale separation necessary for two sets of modes to having negligible mutual energy exchange, with potential consequences in the interpretation of wave turbulence experiments. The methodology presented here provides a general, simple and systematic approach to energy fluxes in wave turbulence.
$w$ that quantifies the scale separation necessary for two sets of modes to having negligible mutual energy exchange, with potential consequences in the interpretation of wave turbulence experiments. The methodology presented here provides a general, simple and systematic approach to energy fluxes in wave turbulence.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 7
- Cited by


