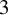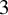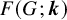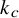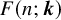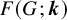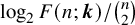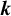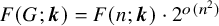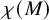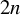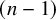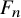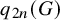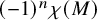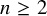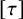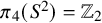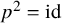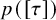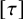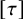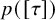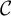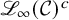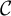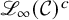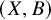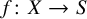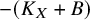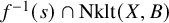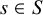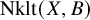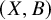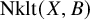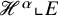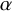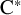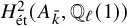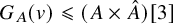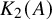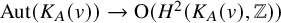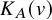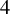Contents
Algebraic and Complex Geometry
Extremal Gromov-Witten invariants of the Hilbert scheme of
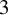 $3$ Points
$3$ Points
- Part of:
-
- Published online by Cambridge University Press:
- 24 March 2023, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Negative moments of orthogonal polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2023, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability for the Erdős-Rothschild problem
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
Minimal Euler characteristics for even-dimensional manifolds with finite fundamental group
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2023, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Geometry and Geometric Analysis
Biharmonic almost complex structures
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
An extension of Venkatesh’s converse theorem to the Selberg class
-
- Published online by Cambridge University Press:
- 31 March 2023, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computational Mathematics
A generalization of Kruskal’s theorem on tensor decomposition
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum
Grassmanniennes affines tordues sur les entiers – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 11 April 2023, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Wonderful compactifications and rational curves with cyclic action
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2023, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
Bordered Floer homology and contact structures
- Part of:
-
- Published online by Cambridge University Press:
- 14 April 2023, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Deformations of arcs and comparison of formal neighborhoods for a curve singularity
- Part of:
-
- Published online by Cambridge University Press:
- 14 April 2023, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
Fluctuations for Some Nonstationary Interacting Particle Systems via Boltzmann–Gibbs Principle
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2023, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
On the connectedness principle and dual complexes for generalized pairs
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2023, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
Thurston’s fragmentation and c-principles
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2023, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Deformations of Log Terminal and Semi Log Canonical Singularities
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2023, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
On sets with unit Hausdorff density in homogeneous groups
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2023, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Superscars for arithmetic point scatters II
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2023, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Angehrn-Siu-Helmke’s method applied to abelian varieties
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2023, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Chaotic tracial dynamics
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2023, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Groups of symplectic involutions on symplectic varieties of Kummer type and their fixed loci
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2023, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation