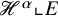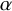1 Introduction
A subset E of a metric space
![]() $(X,d)$
is m
-rectifiable if it can be covered up to an
$(X,d)$
is m
-rectifiable if it can be covered up to an
![]() $\mathscr {H}^m$
-null set, where here, as usual,
$\mathscr {H}^m$
-null set, where here, as usual,
![]() $\mathscr {H}^{\alpha }$
denotes the
$\mathscr {H}^{\alpha }$
denotes the
![]() $\alpha $
-dimensional Hausdorff measure, see [Reference Federer9, Section 2.10.2], by a countable union of Lipschitz images of compact subsets of
$\alpha $
-dimensional Hausdorff measure, see [Reference Federer9, Section 2.10.2], by a countable union of Lipschitz images of compact subsets of
![]() $\mathbb {R}^m$
. It was proved by Kirchheim in [Reference Kirchheim13] that such a set E has Hausdorff density equal to one at almost every point, that is:
$\mathbb {R}^m$
. It was proved by Kirchheim in [Reference Kirchheim13] that such a set E has Hausdorff density equal to one at almost every point, that is:
for
![]() $\mathscr {H}^m$
-almost all
$\mathscr {H}^m$
-almost all
![]() $x\in E$
, where
$x\in E$
, where
![]() $B(x,r)$
denotes the closed unit ball in
$B(x,r)$
denotes the closed unit ball in
![]() $(X,d)$
with centre x and radius r. It is natural to ask whether the converse is true. Namely, does the unit Hausdorff density property imply rectifiability of E? A positive answer, assuming that
$(X,d)$
with centre x and radius r. It is natural to ask whether the converse is true. Namely, does the unit Hausdorff density property imply rectifiability of E? A positive answer, assuming that
![]() $(X,d)$
is Euclidean space, was given by Mattila in the fundamental work [Reference Mattila22], following partial results by Besicovitch [Reference Besicovitch4] and Marstrand [Reference Marstrand20, Reference Marstrand21]. More precisely, the following holds:
$(X,d)$
is Euclidean space, was given by Mattila in the fundamental work [Reference Mattila22], following partial results by Besicovitch [Reference Besicovitch4] and Marstrand [Reference Marstrand20, Reference Marstrand21]. More precisely, the following holds:
Theorem 1.1 (Besicovitch, Marstrand, Mattila).
Fix
![]() $\alpha \ge 0$
, and let
$\alpha \ge 0$
, and let
![]() $E\subset \mathbb {R}^n$
be a Borel subset of Euclidean space, such that
$E\subset \mathbb {R}^n$
be a Borel subset of Euclidean space, such that
![]() $\Theta ^{\alpha }(E,x) = 1$
for
$\Theta ^{\alpha }(E,x) = 1$
for
![]() $\mathscr {H}^{\alpha }$
-almost all
$\mathscr {H}^{\alpha }$
-almost all
![]() $x\in E$
. Then
$x\in E$
. Then
![]() $\alpha $
is an integer and E is
$\alpha $
is an integer and E is
![]() $\alpha $
-rectifiable.
$\alpha $
-rectifiable.
This result is surprising, in that one is able to infer a strong geometric property (the existence of flat,
![]() $\alpha $
-dimensional tangents to E at almost all points) from an a priori much less geometric condition. Note that the unit density condition can be relaxed, to bounds on the lower and upper densities of E, as was shown by Preiss in [Reference Preiss28, Corollary 5.4(3)].
$\alpha $
-dimensional tangents to E at almost all points) from an a priori much less geometric condition. Note that the unit density condition can be relaxed, to bounds on the lower and upper densities of E, as was shown by Preiss in [Reference Preiss28, Corollary 5.4(3)].
In general metric spaces, and for sets of dimension
![]() $1$
, the question was answered by Preiss and Tišer [Reference Preiss and Tišer29]. Their proof uses a variant of the argument by Besicovitch, which is specific to dimension
$1$
, the question was answered by Preiss and Tišer [Reference Preiss and Tišer29]. Their proof uses a variant of the argument by Besicovitch, which is specific to dimension
![]() $1$
and the fact that a continuum with finite
$1$
and the fact that a continuum with finite
![]() $\mathscr {H}^1$
measure is rectifiable. The extension to higher dimensions is still widely open, even in
$\mathscr {H}^1$
measure is rectifiable. The extension to higher dimensions is still widely open, even in
![]() $\mathbb {R}^n$
with a non-Euclidean norm. A relevant partial result has been achieved by Lorent in [Reference Lorent19], where he proved that in
$\mathbb {R}^n$
with a non-Euclidean norm. A relevant partial result has been achieved by Lorent in [Reference Lorent19], where he proved that in
![]() $l_{\infty }^3$
, locally uniform measures are rectifiable. More recently, the second named author in [Reference Merlo24, Reference Merlo25] has proved analogues of Preiss’s rectifiability theorem for
$l_{\infty }^3$
, locally uniform measures are rectifiable. More recently, the second named author in [Reference Merlo24, Reference Merlo25] has proved analogues of Preiss’s rectifiability theorem for
![]() $1$
-codimensional measures in Heisenberg groups and parabolic spaces, see [Reference Merlo, Mourgoglou and Puliatti26], using a notion of rectifiability specific to those spaces. The result in [Reference Merlo, Mourgoglou and Puliatti26] has been obtained in collaboration with Mourgoglou and Puliatti. In this paper, we investigate the structure of Borel sets with unit density for the Hausdorff measure in homogeneous groups (a class of groups that includes Carnot group, see Section 2 for definitions) and we prove:
$1$
-codimensional measures in Heisenberg groups and parabolic spaces, see [Reference Merlo, Mourgoglou and Puliatti26], using a notion of rectifiability specific to those spaces. The result in [Reference Merlo, Mourgoglou and Puliatti26] has been obtained in collaboration with Mourgoglou and Puliatti. In this paper, we investigate the structure of Borel sets with unit density for the Hausdorff measure in homogeneous groups (a class of groups that includes Carnot group, see Section 2 for definitions) and we prove:
Theorem 1.2. Given a homogeneous group
![]() $\mathbb {G}$
, there is a homogeneous norm
$\mathbb {G}$
, there is a homogeneous norm
![]() $||\cdot ||$
on
$||\cdot ||$
on
![]() $\mathbb {G}$
, for which, whenever
$\mathbb {G}$
, for which, whenever
![]() $\alpha \ge 0$
and
$\alpha \ge 0$
and
![]() $E\subset \mathbb {G}$
is such that
$E\subset \mathbb {G}$
is such that
![]() $\mathscr {H}^{\alpha }(E) <+\infty $
, the following are equivalent
$\mathscr {H}^{\alpha }(E) <+\infty $
, the following are equivalent
-
(i)
 $\alpha \in \mathbb {N}$
and E is covered up to an
$\alpha \in \mathbb {N}$
and E is covered up to an
 $\mathscr {H}^{\alpha }$
-null set by countably many Lipschitz images of compact subsets of
$\mathscr {H}^{\alpha }$
-null set by countably many Lipschitz images of compact subsets of
 $\mathbb {R}^{\alpha }$
;
$\mathbb {R}^{\alpha }$
; -
(ii)
 $\Theta ^{\alpha }(E,x) = 1$
for
$\Theta ^{\alpha }(E,x) = 1$
for
 $\mathscr {H}^{\alpha }$
-almost all
$\mathscr {H}^{\alpha }$
-almost all
 $x\in E$
.
$x\in E$
.
Let us briefly discuss the result and its connection with the existing literature. In the Heisenberg groups and in the parabolic spaces [Reference Merlo24, Reference Merlo25, Reference Merlo, Mourgoglou and Puliatti26], the objects that solve the
![]() $1$
-codimensional density problem are not Euclidean rectifiable in general. In both cases, they are just
$1$
-codimensional density problem are not Euclidean rectifiable in general. In both cases, they are just
![]() $1/2$
-Hölder surfaces that can be approximated in the
$1/2$
-Hölder surfaces that can be approximated in the
![]() $1/2$
-Hölder metric by smooth surfaces. Therefore, what our result is implicitly stating is that the Hausdorff density for such high-dimensional intrinsically rectifiable sets, with respect to the natural norm we construct, must be strictly smaller than
$1/2$
-Hölder metric by smooth surfaces. Therefore, what our result is implicitly stating is that the Hausdorff density for such high-dimensional intrinsically rectifiable sets, with respect to the natural norm we construct, must be strictly smaller than
![]() $1$
, and that the sets having unit density for the Hausdorff measure must be low-dimensional. Thus, a more precise assessment of what we prove is the following:
$1$
, and that the sets having unit density for the Hausdorff measure must be low-dimensional. Thus, a more precise assessment of what we prove is the following:
Theorem 1.3. Given a homogeneous group
![]() $\mathbb {G}$
, there is a homogeneous norm
$\mathbb {G}$
, there is a homogeneous norm
![]() $||\cdot ||$
on
$||\cdot ||$
on
![]() $\mathbb {G}$
, for which, whenever
$\mathbb {G}$
, for which, whenever
![]() $\alpha \ge 0$
and
$\alpha \ge 0$
and
![]() $E\subset \mathbb {G}$
is a Borel set for which
$E\subset \mathbb {G}$
is a Borel set for which
![]() $\Theta ^{\alpha }(E,x)=1$
for
$\Theta ^{\alpha }(E,x)=1$
for
![]() $\mathscr {H}^{\alpha }$
-almost every
$\mathscr {H}^{\alpha }$
-almost every
![]() $x\in E$
, then
$x\in E$
, then
![]() $\alpha $
is an integer and varies among the topological dimensions of the homogeneous subgroups of the first layer
$\alpha $
is an integer and varies among the topological dimensions of the homogeneous subgroups of the first layer
![]() $V_1$
of
$V_1$
of
![]() $\mathbb {G}$
and E is
$\mathbb {G}$
and E is
![]() $\alpha $
-rectifiable.
$\alpha $
-rectifiable.
For instance, in the first Heisenberg group
![]() $\mathbb {H}^1$
, the only possible values for
$\mathbb {H}^1$
, the only possible values for
![]() $\alpha $
are
$\alpha $
are
![]() $0$
and
$0$
and
![]() $1$
, while the Hausdorff dimension of
$1$
, while the Hausdorff dimension of
![]() $\mathbb {H}^1$
is
$\mathbb {H}^1$
is
![]() $4$
. This means, in particular, that on high-dimensional (intrinsic) rectifiable sets in Carnot groups, the Hausdorff measure and the spherical Hausdorff measure do not coincide, which is in stark contrast with what happens in Euclidean space (see, for instance, [Reference Federer9, Theorem 3.2.26]).
$4$
. This means, in particular, that on high-dimensional (intrinsic) rectifiable sets in Carnot groups, the Hausdorff measure and the spherical Hausdorff measure do not coincide, which is in stark contrast with what happens in Euclidean space (see, for instance, [Reference Federer9, Theorem 3.2.26]).
Our proof relies on the following observations. First, the Carathéodory construction which yields the measure
![]() $\mathscr {H}^{\alpha }$
is obtained by coverings with arbitrary closed sets. This roughly means that if the
$\mathscr {H}^{\alpha }$
is obtained by coverings with arbitrary closed sets. This roughly means that if the
![]() $\mathscr {H}^{\alpha }$
-measure of a set E is (
$\mathscr {H}^{\alpha }$
-measure of a set E is (
![]() $\sigma $
-)finite, given a set S of very small diameter, say
$\sigma $
-)finite, given a set S of very small diameter, say
![]() $2r$
, containing an
$2r$
, containing an
![]() $x\in E$
, one must have
$x\in E$
, one must have
![]() $\mathscr {H}^{\alpha }(E\cap S)\lesssim (2r)^{\alpha }$
(see Theorem 2.5). On the other hand, item (ii) of Theorem 1.2 implies also
$\mathscr {H}^{\alpha }(E\cap S)\lesssim (2r)^{\alpha }$
(see Theorem 2.5). On the other hand, item (ii) of Theorem 1.2 implies also
![]() $\mathscr {H}^{\alpha }(B(x,r)\cap E)\gtrsim (2r)^{\alpha }$
. Thus, if there exists a set G strictly containing the unit ball but with diameter no larger than
$\mathscr {H}^{\alpha }(B(x,r)\cap E)\gtrsim (2r)^{\alpha }$
. Thus, if there exists a set G strictly containing the unit ball but with diameter no larger than
![]() $2$
, then
$2$
, then
![]() $\mathscr {H}^{\alpha }(x*\delta _r(G)\setminus B(x,r)))/(2r)^{\alpha }$
must be very small (this assumption implies, in particular, that the unit ball is not isodiametric). The second observation is that for specific choices of the metric, such a set G exists and can be chosen in a way that the above constraints force the set E with unit Hausdorff density to be concentrated along the horizontal directions, namely, along
$\mathscr {H}^{\alpha }(x*\delta _r(G)\setminus B(x,r)))/(2r)^{\alpha }$
must be very small (this assumption implies, in particular, that the unit ball is not isodiametric). The second observation is that for specific choices of the metric, such a set G exists and can be chosen in a way that the above constraints force the set E with unit Hausdorff density to be concentrated along the horizontal directions, namely, along
![]() $V_1$
. More precisely, using the first observation at small scales, we prove that E can be covered by
$V_1$
. More precisely, using the first observation at small scales, we prove that E can be covered by
![]() $(1+\varepsilon )$
-Lipschitz graphs above
$(1+\varepsilon )$
-Lipschitz graphs above
![]() $V_1$
for
$V_1$
for
![]() $\varepsilon $
arbitrarily small. Together with the fact that the projection
$\varepsilon $
arbitrarily small. Together with the fact that the projection
![]() $\pi _1$
of
$\pi _1$
of
![]() $\mathbb {G}$
onto the space
$\mathbb {G}$
onto the space
![]() $V_1$
is
$V_1$
is
![]() $1$
-Lipschitz, this implies that the projection
$1$
-Lipschitz, this implies that the projection
![]() $\pi _1(E)$
has Hausdorff density
$\pi _1(E)$
has Hausdorff density
![]() $1$
. As the restriction of our metric to
$1$
. As the restriction of our metric to
![]() $V_1$
is euclidean, we can apply Theorem 1.1 to show that
$V_1$
is euclidean, we can apply Theorem 1.1 to show that
![]() $\pi _1(E)$
is euclidean rectifiable and, using the graph maps above, that E is as well. For the details, see the proof of Theorem 1.3 on page 10.
$\pi _1(E)$
is euclidean rectifiable and, using the graph maps above, that E is as well. For the details, see the proof of Theorem 1.3 on page 10.
In the bulk of the paper, we stick to the smooth-box distance, defined by equation (4.1), as it is a natural metric which makes sense in every homogeneous group and makes the construction and computations relatively easy. A similar construction can be achieved in many other cases, such as for the Koranyi norm in the first Heisenberg group, see Proposition 6.1, and similarly to H-type groups endowed with the gauge norm. On the other hand, we stress that our construction does not work for the Carnot-Carathéodory distance in the Heisenberg group, even though the unit ball for this distance is also far from being isodiametric.
The isodiametric problem in a homogeneous group consists in maximising the volume over all compact sets with diameter at most
![]() $2$
. As discussed above, this problem is deeply connected to that of characterising sets with unit Hausdorff density (see Theorem 3.4). In a finite dimensional vector space, it is known that the unit ball is the unique maximiser, up to translations [Reference Mel’nikov23]. If
$2$
. As discussed above, this problem is deeply connected to that of characterising sets with unit Hausdorff density (see Theorem 3.4). In a finite dimensional vector space, it is known that the unit ball is the unique maximiser, up to translations [Reference Mel’nikov23]. If
![]() $\mathbb {G}$
is a homogeneous group which is not a Banach space, we expect that the unit ball is not isodiametric for any homogeneous norm. Indeed, in homogeneous groups of step
$\mathbb {G}$
is a homogeneous group which is not a Banach space, we expect that the unit ball is not isodiametric for any homogeneous norm. Indeed, in homogeneous groups of step
![]() $2$
or above, there always exists a distance for which the unit ball is not isodiametric, see [Reference Rigot30], and there are many examples of nonisodiametric balls in homogeneous groups [Reference Leonardi, Rigot and Vittone18, Reference Metelichenko27]. The only groups in which we know of a general proof are those in which the diameter of the unit ball is strictly smaller than
$2$
or above, there always exists a distance for which the unit ball is not isodiametric, see [Reference Rigot30], and there are many examples of nonisodiametric balls in homogeneous groups [Reference Leonardi, Rigot and Vittone18, Reference Metelichenko27]. The only groups in which we know of a general proof are those in which the diameter of the unit ball is strictly smaller than
![]() $2$
, such as
$2$
, such as
![]() $\mathbb {R}$
with the snowflake distance
$\mathbb {R}$
with the snowflake distance
![]() $|\cdot |^{1/2}$
. The problem of checking whether in step higher than
$|\cdot |^{1/2}$
. The problem of checking whether in step higher than
![]() $2$
every ball is not isodiametric is hard already in the parabolic plane. One can prove that a vast array of metrics have a ball which is not isodiametric. However, to provide an argument working for any norm, one soon finds technical obstructions. One of the first obstacles is that there are norms in the parabolic plane for which every point of the boundary of the unit ball lies at distance
$2$
every ball is not isodiametric is hard already in the parabolic plane. One can prove that a vast array of metrics have a ball which is not isodiametric. However, to provide an argument working for any norm, one soon finds technical obstructions. One of the first obstacles is that there are norms in the parabolic plane for which every point of the boundary of the unit ball lies at distance
![]() $2$
from another, so that one cannot ‘add a small set’ to the ball, as one does for more usual metrics. Examples of this phenomenon are the balls induced by the norms
$2$
from another, so that one cannot ‘add a small set’ to the ball, as one does for more usual metrics. Examples of this phenomenon are the balls induced by the norms
 $$ \begin{align*} \lVert (x,t) \lVert_1 &:= \lvert x\lvert + \lvert t \lvert^{1/2} \quad \text{(see Remark 3.20 in [27])}\\ \lVert (x,t) \lVert_{\#} &:= \max \{ \lvert x \lvert, \lvert t\lvert^{1/2} - \mathrm{sign}(t)x\}. \end{align*} $$
$$ \begin{align*} \lVert (x,t) \lVert_1 &:= \lvert x\lvert + \lvert t \lvert^{1/2} \quad \text{(see Remark 3.20 in [27])}\\ \lVert (x,t) \lVert_{\#} &:= \max \{ \lvert x \lvert, \lvert t\lvert^{1/2} - \mathrm{sign}(t)x\}. \end{align*} $$
It is worth noting that our result is also relevant when passing from homogeneous groups to the more general context of metric spaces. In [Reference Le Donne16] and [Reference Le Donne and Golo17, Theorem 1.6], it is proved that if a doubling metric measure space has unique tangents at almost every point, then almost all these tangents are metric Lie groups admitting dilations (and if the space is geodesic, then the Lie groups are Carnot groups). These groups are thus ‘universal tangents’, and since density and rectifiability are infinitesimal properties of metric spaces, one could expect that if the convergence to the tangent is ‘fast enough’, our result could be used to prove by blowup the conjecture in a bigger class of metric spaces. The class of metric groups with dilations is larger than that of homogeneous groups, but we prove in Section 5, that any metric group with dilation is biLipschitz equivalent to a group with a slightly more general smooth-box distance for which the unit ball is not isodiametric and the conclusion of Theorem 1.2 holds, meaning that nothing too exotic is to be expected, even though as mentioned above, biLipschitz changes of norm are notoriously difficult to handle for density questions.
The structure of this paper is the following: Section 2 contains notations and basic results on homogeneous groups and measures. Section 3 is devoted to a comparison of the notions of surface measures in Carnot groups. Section 4 contains the proof of Theorem 1.3. In section 5, we address the more general notion of groups with dilations. Finally, in Section 6, we focus on the first Heisenberg group with the Koranyi norm and discuss the full resolution of the density problem in that setting.
2 Preliminaries
We recall that a positive grading of a Lie algebra
![]() $\mathfrak {g}$
is a direct-sum decomposition
$\mathfrak {g}$
is a direct-sum decomposition
![]() $\mathfrak g=V_1\, \oplus \, V_2 \, \oplus \dots \oplus \, V_s$
, for some integer
$\mathfrak g=V_1\, \oplus \, V_2 \, \oplus \dots \oplus \, V_s$
, for some integer
![]() $s\geq 1$
, where
$s\geq 1$
, where
![]() $V_s\neq 0$
and
$V_s\neq 0$
and
![]() $[V_1,V_j]\subseteq V_{j+1}$
for all integers
$[V_1,V_j]\subseteq V_{j+1}$
for all integers
![]() $j\in \{1,\ldots ,s\}$
and where we set
$j\in \{1,\ldots ,s\}$
and where we set
![]() $V_{s+1}=0$
. A positive grading is said to be a stratification, if
$V_{s+1}=0$
. A positive grading is said to be a stratification, if
![]() $[V_1,V_j]=V_{j+1}$
for all
$[V_1,V_j]=V_{j+1}$
for all
![]() $j\in \{1,\ldots ,s\}$
. We also recall that the first layer
$j\in \{1,\ldots ,s\}$
. We also recall that the first layer
![]() $V_1$
of a stratification is usually referred to as the horizontal layer. A homogeneous group
$V_1$
of a stratification is usually referred to as the horizontal layer. A homogeneous group
![]() $\mathbb {G}$
of step s is a connected and simply connected Lie group whose Lie algebra
$\mathbb {G}$
of step s is a connected and simply connected Lie group whose Lie algebra
![]() $\mathfrak g$
admits a positive grading
$\mathfrak g$
admits a positive grading
![]() $\mathfrak g=V_1\, \oplus \, V_2 \, \oplus \dots \oplus \, V_s$
. See [Reference Le Donne15], for precise definitions, in particular, it can be decomposed as a direct sum:
$\mathfrak g=V_1\, \oplus \, V_2 \, \oplus \dots \oplus \, V_s$
. See [Reference Le Donne15], for precise definitions, in particular, it can be decomposed as a direct sum:
where the finite dimensional vector spaces
![]() $V_{\ell }$
are called layers and
$V_{\ell }$
are called layers and
![]() $\kappa $
is the step of
$\kappa $
is the step of
![]() $\mathbb {G}$
. It will always be assumed that
$\mathbb {G}$
. It will always be assumed that
![]() $V_1\neq \{0\}$
(see Remark 2.6). Such a group can be endowed with a family of dilations
$V_1\neq \{0\}$
(see Remark 2.6). Such a group can be endowed with a family of dilations
![]() $(\delta _{\lambda })_{\lambda>0}$
defined by:
$(\delta _{\lambda })_{\lambda>0}$
defined by:
By the Baker-Campbell-Hausdorff formula, up to diffeomorphisms, the group operation can be written as follows, for
![]() $p,q\in \mathbb {G}$
and
$p,q\in \mathbb {G}$
and
![]() $\ell \in \{1,\dots , \kappa \}$
:
$\ell \in \{1,\dots , \kappa \}$
:
where
![]() $Q=(Q_1,\dots ,Q_s):\mathbb {R}^n\times \mathbb {R}^n \to V_1\oplus \ldots \oplus V_s$
, and the
$Q=(Q_1,\dots ,Q_s):\mathbb {R}^n\times \mathbb {R}^n \to V_1\oplus \ldots \oplus V_s$
, and the
![]() $Q_i$
s have the following properties. For any
$Q_i$
s have the following properties. For any
![]() $i=1,\ldots s$
and any
$i=1,\ldots s$
and any
![]() $p,q\in \mathbb {G}$
, we have:
$p,q\in \mathbb {G}$
, we have:
-
(i)
 $Q_i(\delta _{\lambda } p,\delta _{\lambda } q)=\lambda ^iQ_i(p,q)$
,
$Q_i(\delta _{\lambda } p,\delta _{\lambda } q)=\lambda ^iQ_i(p,q)$
, -
(ii)
 $Q_i(p,q)=-Q_i(-q,-p)$
,
$Q_i(p,q)=-Q_i(-q,-p)$
, -
(iii)
 $Q_1=0$
and
$Q_1=0$
and
 $Q_i(p,q)=Q_i(p_1,\ldots ,p_{i-1},q_1,\ldots ,q_{i-1})$
.
$Q_i(p,q)=Q_i(p_1,\ldots ,p_{i-1},q_1,\ldots ,q_{i-1})$
.
Definition 2.1 (Homogeneous norm, homogeneous distance).
A distance
![]() $d:\mathbb {G}\times \mathbb {G}\to \mathbb {R}$
is homogeneous and left-invariant if for any
$d:\mathbb {G}\times \mathbb {G}\to \mathbb {R}$
is homogeneous and left-invariant if for any
![]() $x,y\in \mathbb {G}$
, there holds
$x,y\in \mathbb {G}$
, there holds
-
(i)
 $d(\delta _{\lambda } x,\delta _{\lambda } y)=\lambda d(x,y)$
for any
$d(\delta _{\lambda } x,\delta _{\lambda } y)=\lambda d(x,y)$
for any
 $\lambda>0$
,
$\lambda>0$
, -
(ii)
 $d(z *x,z* y)=d(x,y)$
for any
$d(z *x,z* y)=d(x,y)$
for any
 $z\in \mathbb {G}$
.
$z\in \mathbb {G}$
.
It is equivalent to define a homogeneous distance d and a homogeneous norm
![]() $||\cdot ||$
, as can be seen by writing
$||\cdot ||$
, as can be seen by writing
In the following, d is a left-invariant homogeneous metric on
![]() $\mathbb G$
and the corresponding closed ball with centre
$\mathbb G$
and the corresponding closed ball with centre
![]() $x\in \mathbb G$
and radius
$x\in \mathbb G$
and radius
![]() $r>0$
is denoted by
$r>0$
is denoted by
![]() $\mathrm {B}_d(x,r)$
. We will drop the subscript d when there is no ambiguity. As the first layer
$\mathrm {B}_d(x,r)$
. We will drop the subscript d when there is no ambiguity. As the first layer
![]() $V_1$
is assumed to be nondegenerate, the balls
$V_1$
is assumed to be nondegenerate, the balls
![]() $B_d(x,r)$
have diameter
$B_d(x,r)$
have diameter
![]() $2r$
. The following result, the elementary proof of which we learned in Metelichenko’s thesis [Reference Metelichenko27, Lemma 3.17], will be very useful.
$2r$
. The following result, the elementary proof of which we learned in Metelichenko’s thesis [Reference Metelichenko27, Lemma 3.17], will be very useful.
Proposition 2.2. If
![]() $||\cdot ||$
is a homogeneous norm on
$||\cdot ||$
is a homogeneous norm on
![]() $\mathbb {G}$
, then its restriction
$\mathbb {G}$
, then its restriction
![]() $|\cdot |$
to
$|\cdot |$
to
![]() $V_1$
is a vector space norm. Also, if
$V_1$
is a vector space norm. Also, if
![]() $\pi _1$
denotes the projection
$\pi _1$
denotes the projection
![]() $\mathbb {G}\to V_1$
,
$\mathbb {G}\to V_1$
,
![]() $(x_1,\dots ,x_{\kappa }) \mapsto x_1$
, then
$(x_1,\dots ,x_{\kappa }) \mapsto x_1$
, then
![]() $\pi _1$
is exactly
$\pi _1$
is exactly
![]() $1$
-Lipschitz with the norm
$1$
-Lipschitz with the norm
![]() $|\cdot |$
on
$|\cdot |$
on
![]() $V_1$
.
$V_1$
.
Proof. As
![]() $\pi _1(x_1,0,\dots ,0) = x_1,$
the projection
$\pi _1(x_1,0,\dots ,0) = x_1,$
the projection
![]() $\pi _1$
cannot have Lipschitz constant smaller than one. In order to prove the opposite bound, note that
$\pi _1$
cannot have Lipschitz constant smaller than one. In order to prove the opposite bound, note that
![]() $\pi _1$
is a group morphism, thus, it suffices to show that
$\pi _1$
is a group morphism, thus, it suffices to show that
![]() $\lvert \pi _1(x)\rvert \le ||x||$
for
$\lvert \pi _1(x)\rvert \le ||x||$
for
![]() $x\in \mathbb {G}$
. Fix
$x\in \mathbb {G}$
. Fix
![]() $x=(x_1,\dots ,x_{\kappa })\in \mathbb {G}$
. On the one hand, there holds
$x=(x_1,\dots ,x_{\kappa })\in \mathbb {G}$
. On the one hand, there holds
![]() $||\delta _{1/2}(x*x)|| = ||x*x||/2 \le ||x||$
, and on the other hand:
$||\delta _{1/2}(x*x)|| = ||x*x||/2 \le ||x||$
, and on the other hand:
Iterating this operation, and noting that
![]() $\delta _{1/2^n}((x*x)*\dots *(x*x)) \to (x_1, 0,\dots , 0)$
, one gets
$\delta _{1/2^n}((x*x)*\dots *(x*x)) \to (x_1, 0,\dots , 0)$
, one gets
![]() $||(x_1,0,\dots ,0)||\le ||x||$
. Finally, given
$||(x_1,0,\dots ,0)||\le ||x||$
. Finally, given
![]() $x_1$
and
$x_1$
and
![]() $y_1$
in
$y_1$
in
![]() $V_1$
, there holds
$V_1$
, there holds
and thus,
![]() $|\cdot |$
is a (vector-space) norm on
$|\cdot |$
is a (vector-space) norm on
![]() $V_1$
, since homogeneity and positivity are immediate.
$V_1$
, since homogeneity and positivity are immediate.
Since one of the themes of the paper is the distinction between the various types of Hausdorff measures, we introduce them here.
Definition 2.3 (Hausdorff and spherical measures).
For
![]() $\alpha \ge 0$
, define the
$\alpha \ge 0$
, define the
![]() $\alpha $
-dimensional Hausdorff measure relative to the left-invariant homogeneous distance d
$\alpha $
-dimensional Hausdorff measure relative to the left-invariant homogeneous distance d

Along with the Hausdorff measure, it is useful to study other surface measures, we will focus on two of them: the
![]() $\alpha $
-dimensional spherical measure:
$\alpha $
-dimensional spherical measure:

and the
![]() $\alpha $
-dimensional centred spherical measure:
$\alpha $
-dimensional centred spherical measure:
where

These three measures are Borel regular outer measures and are mutually absolutely continuous, more precisely,
![]() $\mathscr {H}^{\alpha }\leq \mathscr {S}^{\alpha }\leq \mathscr {C}^{\alpha } \leq 2^{\alpha }\mathscr {H}^{\alpha }$
.
$\mathscr {H}^{\alpha }\leq \mathscr {S}^{\alpha }\leq \mathscr {C}^{\alpha } \leq 2^{\alpha }\mathscr {H}^{\alpha }$
.
Definition 2.4 (Lower and upper densities).
If
![]() $\phi $
is a Radon measure on
$\phi $
is a Radon measure on
![]() $\mathbb {G}$
, and
$\mathbb {G}$
, and
![]() $\alpha>0$
, define the lower and upper
$\alpha>0$
, define the lower and upper
![]() $\alpha $
-densities of
$\alpha $
-densities of
![]() $\phi $
at x by
$\phi $
at x by
If the upper and lower densities coincide, their value is called the density of
![]() $\phi $
at x. If
$\phi $
at x. If
![]() $\phi = \mathscr {H}^{\alpha } \llcorner E$
, where E is a subset of
$\phi = \mathscr {H}^{\alpha } \llcorner E$
, where E is a subset of
![]() $\mathbb {G}$
, its density (respectively, upper, lower densities) is also called Hausdorff density of E and denoted
$\mathbb {G}$
, its density (respectively, upper, lower densities) is also called Hausdorff density of E and denoted
![]() $\Theta ^{\alpha }(E,x)$
.
$\Theta ^{\alpha }(E,x)$
.
The following fundamental result on Hausdorff measures lies at the core of this paper. It is a consequence of [Reference Federer9, Theorems 2.10.17 and 2.10.18] (see also Theorem 2.1 and Lemma 3.1 in [Reference Julia, Nicolussi Golo and Vittone12]).
Proposition 2.5. Suppose that
![]() $E\subset \mathbb {G}$
is a Borel set of
$E\subset \mathbb {G}$
is a Borel set of
![]() $\mathscr {H}^{\alpha }$
-finite measure. Then for
$\mathscr {H}^{\alpha }$
-finite measure. Then for
![]() $\mathscr {H}^{\alpha }$
-almost every
$\mathscr {H}^{\alpha }$
-almost every
![]() $x\in E$
, there holds:
$x\in E$
, there holds:

Moreover, in the case
![]() $E=\mathbb {G}$
, denoting by Q the homogeneous dimension of
$E=\mathbb {G}$
, denoting by Q the homogeneous dimension of
![]() $\mathbb {G}$
, for
$\mathbb {G}$
, for
![]() $x\in \mathbb {G}$
, there holds:
$x\in \mathbb {G}$
, there holds:

There is a degenerate case, which needs to be ruled out:
Proposition 2.6. If
![]() $V_1=\{0\}$
, then sets with unit Hausdorff density are necessarily of dimension
$V_1=\{0\}$
, then sets with unit Hausdorff density are necessarily of dimension
![]() $0$
.
$0$
.
Proof. First, let us show that a ball of radius r in such a group necessarily has diameter strictly less than
![]() $2r$
.
$2r$
.
In order to see this, let
![]() $\ell $
be the index of the first nontrivial layer and denote by
$\ell $
be the index of the first nontrivial layer and denote by
![]() $\mathbb {G}'$
the homogeneous group obtained from
$\mathbb {G}'$
the homogeneous group obtained from
![]() $\mathbb {G}$
by dividing by
$\mathbb {G}$
by dividing by
![]() $\ell $
the homogeneity of each layer of
$\ell $
the homogeneity of each layer of
![]() $\mathbb {G}$
. It is immediate to see that
$\mathbb {G}$
. It is immediate to see that
![]() $||\cdot ||^{\ell }$
is a norm on the homogeneous group
$||\cdot ||^{\ell }$
is a norm on the homogeneous group
![]() $\mathbb {G}'$
. Since the unit ball
$\mathbb {G}'$
. Since the unit ball
![]() $B(0,1)$
is the same in
$B(0,1)$
is the same in
![]() $\mathbb {G}$
and
$\mathbb {G}$
and
![]() $\mathbb {G}'$
, on the one hand, thanks to Proposition 2.2, we know that the diameter of
$\mathbb {G}'$
, on the one hand, thanks to Proposition 2.2, we know that the diameter of
![]() $B(0,1)$
in
$B(0,1)$
in
![]() $\mathbb {G}'$
is
$\mathbb {G}'$
is
![]() $2$
because the group has nontrivial first layer, on the other, in
$2$
because the group has nontrivial first layer, on the other, in
![]() $\mathbb {G}$
, its diameter is
$\mathbb {G}$
, its diameter is
![]() $2^{1/\ell }<2$
. By homogeneity, there exists
$2^{1/\ell }<2$
. By homogeneity, there exists
![]() $\varepsilon>0$
, such that
$\varepsilon>0$
, such that
![]() $\mathrm {diam}(B(x,r)) \le (1-\varepsilon ) (2r)$
for all
$\mathrm {diam}(B(x,r)) \le (1-\varepsilon ) (2r)$
for all
![]() $x\in \mathbb {G}$
and all
$x\in \mathbb {G}$
and all
![]() $r>0$
. Given
$r>0$
. Given
![]() $E\subset \mathbb {G}$
with Hausdorff
$E\subset \mathbb {G}$
with Hausdorff
![]() $\alpha $
-density
$\alpha $
-density
![]() $1 \mathscr {H}^{\alpha }$
-almost everywhere, using the first statement of Proposition 2.5 at a point where it holds, for small enough
$1 \mathscr {H}^{\alpha }$
-almost everywhere, using the first statement of Proposition 2.5 at a point where it holds, for small enough
![]() $r>0$
, one gets
$r>0$
, one gets
Dividing by
![]() $(2r)^{\alpha }$
and letting r go to zero contradicts the Hausdorff density hypothesis if
$(2r)^{\alpha }$
and letting r go to zero contradicts the Hausdorff density hypothesis if
![]() $\alpha>0$
.
$\alpha>0$
.
3 Comparison of surface measures in Carnot groups
Throughout this section,
![]() $\mathbb {G}$
will be a fixed Carnot group and d a fixed homogeneous left-invariant distance on
$\mathbb {G}$
will be a fixed Carnot group and d a fixed homogeneous left-invariant distance on
![]() $\mathbb {G}$
.
$\mathbb {G}$
.
Definition 3.1 (
 $C^1_{\mathrm H}(\mathbb {G}, \mathbb {G}')$
-rectifiable sets).
$C^1_{\mathrm H}(\mathbb {G}, \mathbb {G}')$
-rectifiable sets).
Let
![]() $\mathbb G'$
be another Carnot group endowed with the left-invariant homogeneous distance
$\mathbb G'$
be another Carnot group endowed with the left-invariant homogeneous distance
![]() $d'$
. Let
$d'$
. Let
![]() $\Omega \subseteq \mathbb G$
be open, and let
$\Omega \subseteq \mathbb G$
be open, and let
![]() $f:\Omega \to \mathbb G'$
be a map. We say that f is Pansu differentiable at
$f:\Omega \to \mathbb G'$
be a map. We say that f is Pansu differentiable at
![]() $x\in \Omega $
if there exists a homogeneous homomorphism
$x\in \Omega $
if there exists a homogeneous homomorphism
![]() $Df_x:\mathbb G\to \mathbb G'$
, such that
$Df_x:\mathbb G\to \mathbb G'$
, such that
 $$ \begin{align*}\lim_{y\to x}\frac{d'(f(x)^{-1}\cdot f(y),Df_x(x^{-1}\cdot y))}{d(x,y)}=0. \end{align*} $$
$$ \begin{align*}\lim_{y\to x}\frac{d'(f(x)^{-1}\cdot f(y),Df_x(x^{-1}\cdot y))}{d(x,y)}=0. \end{align*} $$
Moreover, we say that f is of class
![]() $C^1_{\mathrm H}$
in
$C^1_{\mathrm H}$
in
![]() $\Omega $
if the map
$\Omega $
if the map
![]() $x\mapsto Df_x$
is continuous from
$x\mapsto Df_x$
is continuous from
![]() $\Omega $
to the space of homogeneous homomorphisms from
$\Omega $
to the space of homogeneous homomorphisms from
![]() $\mathbb G$
to
$\mathbb G$
to
![]() $\mathbb G'$
. Given an arbitrary Carnot group
$\mathbb G'$
. Given an arbitrary Carnot group
![]() $\mathbb G$
, we say that
$\mathbb G$
, we say that
![]() $\Gamma \subseteq \mathbb G$
is a
$\Gamma \subseteq \mathbb G$
is a
![]() $C^1_{\mathrm H}$
-submanifold of
$C^1_{\mathrm H}$
-submanifold of
![]() $\mathbb G$
if there exists a Carnot group
$\mathbb G$
if there exists a Carnot group
![]() $\mathbb G'$
, such that for every
$\mathbb G'$
, such that for every
![]() $p\in \Gamma $
, there exists an open neighbourhood
$p\in \Gamma $
, there exists an open neighbourhood
![]() $\Omega $
of p and a function
$\Omega $
of p and a function
![]() $f\in C^1_{\mathrm H}(\Omega ;\mathbb G')$
, such that
$f\in C^1_{\mathrm H}(\Omega ;\mathbb G')$
, such that
and
![]() $Df_p:\mathbb G\to \mathbb G'$
is surjective and
$Df_p:\mathbb G\to \mathbb G'$
is surjective and
![]() ${\mathrm Ker}(Df_p)$
admits a complementary subgroup. In this case, we say that
${\mathrm Ker}(Df_p)$
admits a complementary subgroup. In this case, we say that
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $C^1_{\mathrm H}(\mathbb G,\mathbb G')$
-submanifold. Finally, we say that
$C^1_{\mathrm H}(\mathbb G,\mathbb G')$
-submanifold. Finally, we say that
![]() $\Gamma \subseteq \mathbb G$
is a
$\Gamma \subseteq \mathbb G$
is a
![]() $(\mathbb G,\mathbb G')$
-rectifiable set if
$(\mathbb G,\mathbb G')$
-rectifiable set if
![]() $\mathscr {H}^{Q-Q'}(\Gamma ) <+\infty $
and there exist countably many subsets
$\mathscr {H}^{Q-Q'}(\Gamma ) <+\infty $
and there exist countably many subsets
![]() $\Gamma _i$
of
$\Gamma _i$
of
![]() $\mathbb G$
that are
$\mathbb G$
that are
![]() $C^1_{\mathrm H}(\mathbb G,\mathbb G')$
-submanifolds, such that
$C^1_{\mathrm H}(\mathbb G,\mathbb G')$
-submanifolds, such that
 $$ \begin{align*}\mathscr{H}^{\mathcal{Q}-\mathcal{Q}'}\left(\Gamma\setminus\bigcup_{i=1}^{+\infty}\Gamma_i\right)=0. \end{align*} $$
$$ \begin{align*}\mathscr{H}^{\mathcal{Q}-\mathcal{Q}'}\left(\Gamma\setminus\bigcup_{i=1}^{+\infty}\Gamma_i\right)=0. \end{align*} $$
At
![]() $\mathscr {H}^{Q-Q'}\llcorner \Gamma $
-almost every point x,
$\mathscr {H}^{Q-Q'}\llcorner \Gamma $
-almost every point x,
![]() $\Gamma $
admits a tangent
$\Gamma $
admits a tangent
![]() $\mathbb {V}(x)$
, which is a homogeneous subgroup of
$\mathbb {V}(x)$
, which is a homogeneous subgroup of
![]() $\mathbb {G}$
with homogeneous dimension
$\mathbb {G}$
with homogeneous dimension
![]() $Q-Q'$
.
$Q-Q'$
.
Definition 3.2 (Tangent measures).
Let
![]() $\phi $
be a Radon measure on
$\phi $
be a Radon measure on
![]() $\mathbb G$
. For any
$\mathbb G$
. For any
![]() $x\in \mathbb G$
and any
$x\in \mathbb G$
and any
![]() $r>0$
, we define the rescaled measure
$r>0$
, we define the rescaled measure
The
![]() $\alpha $
-dimensional tangents to
$\alpha $
-dimensional tangents to
![]() $\phi $
at x are the Radon measures
$\phi $
at x are the Radon measures
![]() $\nu $
, which are weak* limits of a sequence
$\nu $
, which are weak* limits of a sequence
![]() $r_i^{-\alpha } T_{x,r_i} \phi $
for
$r_i^{-\alpha } T_{x,r_i} \phi $
for
![]() $r_i\to 0$
. The set of these measures is denoted by
$r_i\to 0$
. The set of these measures is denoted by
![]() $\mathrm {Tan}_{\alpha }(\phi ,x)$
.
$\mathrm {Tan}_{\alpha }(\phi ,x)$
.
Definition 3.3. Let
![]() $\phi $
be a Radon measure in
$\phi $
be a Radon measure in
![]() $\mathbb {G}$
, and let
$\mathbb {G}$
, and let
![]() $h\in \mathbb {N}$
. We say that
$h\in \mathbb {N}$
. We say that
![]() $\phi $
is
$\phi $
is
![]() $\mathscr {P}_h$
-rectifiable if
$\mathscr {P}_h$
-rectifiable if
-
(i)
 $0<\Theta ^h_*(\phi ,x)\leq \Theta ^{h,*}(\phi ,x)<\infty $
for
$0<\Theta ^h_*(\phi ,x)\leq \Theta ^{h,*}(\phi ,x)<\infty $
for
 $\phi $
-almost every
$\phi $
-almost every
 $x\in \mathbb {G}$
;
$x\in \mathbb {G}$
; -
(ii) for
 $\phi $
-almost every
$\phi $
-almost every
 $x\in \mathbb {G}$
, there exists a homogeneous subgroup
$x\in \mathbb {G}$
, there exists a homogeneous subgroup
 $\mathbb V(x)$
of
$\mathbb V(x)$
of
 $\mathbb {G}$
of Hausdorff dimension
$\mathbb {G}$
of Hausdorff dimension
 $h\in \mathbb {N}$
, such that
$h\in \mathbb {N}$
, such that
 $\mathrm {Tan}_h(\phi ,x)\subseteq \{\lambda \mathscr {H}^h\llcorner \mathbb V(x):\lambda>0\}$
.
$\mathrm {Tan}_h(\phi ,x)\subseteq \{\lambda \mathscr {H}^h\llcorner \mathbb V(x):\lambda>0\}$
.
The various surface measures on
![]() $(\mathbb {G},\mathbb {G}')$
-rectifiable sets are now well understood, as summed up in the following statement which is a combination of [Reference Antonelli and Merlo1, Theorem 1.1], [Reference Antonelli and Merlo2, Proposition 5.2], as well as the results of [Reference Julia, Nicolussi Golo and Vittone12].
$(\mathbb {G},\mathbb {G}')$
-rectifiable sets are now well understood, as summed up in the following statement which is a combination of [Reference Antonelli and Merlo1, Theorem 1.1], [Reference Antonelli and Merlo2, Proposition 5.2], as well as the results of [Reference Julia, Nicolussi Golo and Vittone12].
Theorem 3.4. Suppose that
![]() $\Gamma \subseteq \mathbb G$
is a Borel,
$\Gamma \subseteq \mathbb G$
is a Borel,
![]() $(\mathbb {G},\mathbb {G}')$
-rectifiable set. Then
$(\mathbb {G},\mathbb {G}')$
-rectifiable set. Then
![]() $\mathscr {H}^{Q-Q'}\llcorner \Gamma $
,
$\mathscr {H}^{Q-Q'}\llcorner \Gamma $
,
![]() $\mathscr S^{Q-Q'}\llcorner \Gamma $
and
$\mathscr S^{Q-Q'}\llcorner \Gamma $
and
![]() $\mathscr C^{Q-Q'} \llcorner \Gamma $
are
$\mathscr C^{Q-Q'} \llcorner \Gamma $
are
![]() $\mathscr {P}_{Q-Q'}$
-rectifiable. Furthermore, at almost every point
$\mathscr {P}_{Q-Q'}$
-rectifiable. Furthermore, at almost every point
![]() $x\in \Gamma $
$x\in \Gamma $
Finally, letting
![]() $\mathbb {V}(x)$
be the
$\mathbb {V}(x)$
be the
![]() $Q-Q'$
subgroup for which part (ii) of Definition 3.3 is satisfied
$Q-Q'$
subgroup for which part (ii) of Definition 3.3 is satisfied
where for a homogeneous subgroup
![]() $\mathbb {V}$
of
$\mathbb {V}$
of
![]() $\mathbb {G}$
with dimension
$\mathbb {G}$
with dimension
![]() $Q-Q'$
and a Haar measure
$Q-Q'$
and a Haar measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {V}$
, we write:
$\mathbb {V}$
, we write:
The above result tells us that the coefficients that allow to express the Hausdorff measure on smooth surfaces in terms of the centred Hausdorff measure or the spherical Hausdorff measure are almost everywhere the volume of the isodiametric is set in the tangents. (with respect to the centred or the spherical measures)
Corollary 3.5. Under the hypotheses of Theorem 3.4 and at a point x where its conclusions holds, suppose that
Then the intersection of
![]() $B(0,1)$
with
$B(0,1)$
with
![]() $\mathbb {V}(x)$
is an isodiametric shape in the homogeneous group
$\mathbb {V}(x)$
is an isodiametric shape in the homogeneous group
![]() $\mathbb {V}(x)$
with the metric given by the restriction of d.
$\mathbb {V}(x)$
with the metric given by the restriction of d.
Proof. Combining the Hausdorff density hypothesis (3.3) and the centred spherical density property (3.2) yields

However, since
![]() $\mathscr {C}^{Q-Q'}\llcorner \Gamma $
is
$\mathscr {C}^{Q-Q'}\llcorner \Gamma $
is
![]() $\mathscr {P}^{Q-Q'}$
-rectifiable and thanks to (3.2), there also holds
$\mathscr {P}^{Q-Q'}$
-rectifiable and thanks to (3.2), there also holds
 $$\begin{align*}\dfrac{(\mathscr{C}^{Q-Q'}\llcorner \mathbb{V}(x) )(B(0,1))}{2^{(Q-Q')}} = \lim_{r\to 0}\dfrac{(\mathscr{C}^{Q-Q'}\llcorner \Gamma )(B(x,r))}{(2r)^{(Q-Q')}} = 1, \end{align*}$$
$$\begin{align*}\dfrac{(\mathscr{C}^{Q-Q'}\llcorner \mathbb{V}(x) )(B(0,1))}{2^{(Q-Q')}} = \lim_{r\to 0}\dfrac{(\mathscr{C}^{Q-Q'}\llcorner \Gamma )(B(x,r))}{(2r)^{(Q-Q')}} = 1, \end{align*}$$
which implies that
![]() $B(0,1)$
realises the supremum of the right-hand side of (3.4). Therefore, the restriction of the unit ball
$B(0,1)$
realises the supremum of the right-hand side of (3.4). Therefore, the restriction of the unit ball
![]() $B(0,1)\cap \mathbb {V}(x)$
is isodiametric in the group
$B(0,1)\cap \mathbb {V}(x)$
is isodiametric in the group
![]() $\mathbb {V}(x)$
endowed with the restriction of the metric d.
$\mathbb {V}(x)$
endowed with the restriction of the metric d.
4 Sets with Hausdorff density
 $1$
in homogeneous groups
$1$
in homogeneous groups
One can endow a homogeneous group
![]() $\mathbb {G}$
as above with a smooth-box homogeneous norm of the form
$\mathbb {G}$
as above with a smooth-box homogeneous norm of the form
where
![]() $|x_{\ell }|$
stands for the euclidean norm of the vector
$|x_{\ell }|$
stands for the euclidean norm of the vector
![]() $x_{\ell }\in V_{\ell }$
and where
$x_{\ell }\in V_{\ell }$
and where
![]() $\varepsilon _1=1$
. In all the following, we suppose
$\varepsilon _1=1$
. In all the following, we suppose
![]() $\kappa \ge 2$
. Throughout the rest of this section, we will denote by
$\kappa \ge 2$
. Throughout the rest of this section, we will denote by
![]() $B(x,r)$
the ball of centre x and radius
$B(x,r)$
the ball of centre x and radius
![]() $r>0$
relative to the metric induced by the norm in (4.1). For a proof of the following lemma, we refer to the appendix of [Reference Franchi, Serapioni and Serra Cassano11].
$r>0$
relative to the metric induced by the norm in (4.1). For a proof of the following lemma, we refer to the appendix of [Reference Franchi, Serapioni and Serra Cassano11].
Lemma 4.1. Provided the
![]() $\varepsilon _{\ell }$
are small enough with respect to
$\varepsilon _{\ell }$
are small enough with respect to
![]() $\varepsilon _1,\dots ,\varepsilon _{\ell -1}$
, then the function (4.1) defines a homogeneous norm, and thus a metric, on
$\varepsilon _1,\dots ,\varepsilon _{\ell -1}$
, then the function (4.1) defines a homogeneous norm, and thus a metric, on
![]() $\mathbb {G}$
.
$\mathbb {G}$
.
The unit ball of this homogeneous norm is not isodiametric, indeed, it is easy to find a strictly larger set diameter
![]() $2$
. Fix
$2$
. Fix
![]() $19/10<\xi <2$
. Throughout the rest of the section, we choose
$19/10<\xi <2$
. Throughout the rest of the section, we choose
![]() $\varepsilon _2,\ldots ,\varepsilon _{\kappa }$
in such a way that the conclusion of Lemma 4.1 holds and
$\varepsilon _2,\ldots ,\varepsilon _{\kappa }$
in such a way that the conclusion of Lemma 4.1 holds and
Proposition 4.2. Let
![]() $\xi $
be the parameter chosen above, and define the set
$\xi $
be the parameter chosen above, and define the set
![]() $G(0,1)$
as the family of those
$G(0,1)$
as the family of those
![]() $(x_1,x_2,\ldots , x_{\kappa })=x\in \mathbb {G}$
for which
$(x_1,x_2,\ldots , x_{\kappa })=x\in \mathbb {G}$
for which
If the
![]() $\varepsilon _1,\ldots ,\varepsilon _{\kappa }$
are chosen small enough with respect to the
$\varepsilon _1,\ldots ,\varepsilon _{\kappa }$
are chosen small enough with respect to the
![]() $\tilde c_{\ell }$
, then the diameter of the set
$\tilde c_{\ell }$
, then the diameter of the set
![]() $G(0,1)$
is
$G(0,1)$
is
![]() $2$
and
$2$
and
![]() $B(0,1)\subseteq G(0,1)$
.
$B(0,1)\subseteq G(0,1)$
.
Proof. Checking layer by layer, one sees that
![]() $B(0,1)\subset G(0,1)\subset B(0,2)$
. It remains to prove that if
$B(0,1)\subset G(0,1)\subset B(0,2)$
. It remains to prove that if
![]() $x,y$
are points in
$x,y$
are points in
![]() $G(0,1)$
, there holds
$G(0,1)$
, there holds
![]() $||x^{-1}*y|| \le 2$
. This is also done layer by layer: for the first layer, one immediately has
$||x^{-1}*y|| \le 2$
. This is also done layer by layer: for the first layer, one immediately has
![]() $|y_1-x_1| \le 2$
. From the second layer onward, that is, for
$|y_1-x_1| \le 2$
. From the second layer onward, that is, for
![]() $\ell \geq 2$
, we have
$\ell \geq 2$
, we have
 $$ \begin{align} \varepsilon_{\ell}^{\ell}\lvert \pi_{\ell} (x^{-1}*y)\rvert &= \varepsilon_{\ell}^{\ell}\lvert -x_{\ell}+y_{\ell}+{Q}_{\ell}(-x_1,\ldots,-x_{\ell-1},y_1,\ldots,y_{\ell-1})\rvert \nonumber\\ &\leq \varepsilon_{\ell}^{\ell}\lvert x_{\ell}\rvert+\varepsilon_{\ell}^{\ell}\lvert y_{\ell}\rvert+\varepsilon_{\ell}^{\ell}\lvert{Q}_{\ell}(-x_1,\ldots,-x_{\ell-1},y_1,\ldots,y_{\ell-1})\rvert\\ &\leq 2\xi^{\ell-1}+\varepsilon_{\ell}^{\ell}\lvert{Q}_{\ell}(-x_1,\ldots,-x_{\ell-1},y_1,\ldots,y_{\ell-1})\rvert. \nonumber\end{align} $$
$$ \begin{align} \varepsilon_{\ell}^{\ell}\lvert \pi_{\ell} (x^{-1}*y)\rvert &= \varepsilon_{\ell}^{\ell}\lvert -x_{\ell}+y_{\ell}+{Q}_{\ell}(-x_1,\ldots,-x_{\ell-1},y_1,\ldots,y_{\ell-1})\rvert \nonumber\\ &\leq \varepsilon_{\ell}^{\ell}\lvert x_{\ell}\rvert+\varepsilon_{\ell}^{\ell}\lvert y_{\ell}\rvert+\varepsilon_{\ell}^{\ell}\lvert{Q}_{\ell}(-x_1,\ldots,-x_{\ell-1},y_1,\ldots,y_{\ell-1})\rvert\\ &\leq 2\xi^{\ell-1}+\varepsilon_{\ell}^{\ell}\lvert{Q}_{\ell}(-x_1,\ldots,-x_{\ell-1},y_1,\ldots,y_{\ell-1})\rvert. \nonumber\end{align} $$
Recall that each entry of
![]() $Q_{\ell }:(V_1\oplus \ldots \oplus V_{\ell -1})\times (V_1\oplus \ldots \oplus V_{\ell -1})\to V_{\ell }$
is a polynomial in the components of x and y of order lower than
$Q_{\ell }:(V_1\oplus \ldots \oplus V_{\ell -1})\times (V_1\oplus \ldots \oplus V_{\ell -1})\to V_{\ell }$
is a polynomial in the components of x and y of order lower than
![]() $\ell $
, and is
$\ell $
, and is
![]() $\ell $
homogeneous with respect to the group dilations. Hence, following the footsteps of [Reference Franchi, Serapioni and Serra Cassano11], we can find positive real numbers
$\ell $
homogeneous with respect to the group dilations. Hence, following the footsteps of [Reference Franchi, Serapioni and Serra Cassano11], we can find positive real numbers
![]() $\tilde c_{\ell }>0$
, such that
$\tilde c_{\ell }>0$
, such that
 $$ \begin{align} \begin{aligned} |Q_{\ell} (x,y)| &\le \sum_{j=1}^{\ell-1} c_{j,\ell} ||x||^j||y||^{\ell-j}\leq \tilde{c}_{\ell}\sum_{j=1}^{\ell-1} \binom{\ell}{j} ||x||^j||y||^{\ell-j}\\ &\leq \tilde{c}_{\ell}(||x||+||y||)^{\ell}\leq 2^{\ell-1}\tilde{c}_{\ell}(||x||^{\ell}+||y||^{\ell}), \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} |Q_{\ell} (x,y)| &\le \sum_{j=1}^{\ell-1} c_{j,\ell} ||x||^j||y||^{\ell-j}\leq \tilde{c}_{\ell}\sum_{j=1}^{\ell-1} \binom{\ell}{j} ||x||^j||y||^{\ell-j}\\ &\leq \tilde{c}_{\ell}(||x||+||y||)^{\ell}\leq 2^{\ell-1}\tilde{c}_{\ell}(||x||^{\ell}+||y||^{\ell}), \end{aligned}\end{align} $$
where the last inequality above comes from Jensen’s inequality. The above chain of inequalities together with (4.2) and (4.3) implies
 $$\begin{align*} \varepsilon_{\ell}^{\ell}\lvert \pi_{\ell} (x^{-1}*y)\rvert &= \varepsilon_{\ell}^{\ell}\lvert -x_{\ell}+y_{\ell}+{Q}_{\ell}(-x_1,\ldots,-x_{\ell-1},y_1,\ldots,y_{\ell-1})\rvert\\ &\leq 2\xi^{\ell-1}+2^{\ell-1}\varepsilon_{\ell}^{\ell}\tilde{c}_{\ell}(||x||^{\ell}+||y||^{\ell})\\ &\leq 2\xi^{\ell-1}+2^{\ell-1}\varepsilon_{\ell}^{\ell}\tilde{c}_{\ell}\cdot2 \leq 2^{\ell}, \nonumber \end{align*}$$
$$\begin{align*} \varepsilon_{\ell}^{\ell}\lvert \pi_{\ell} (x^{-1}*y)\rvert &= \varepsilon_{\ell}^{\ell}\lvert -x_{\ell}+y_{\ell}+{Q}_{\ell}(-x_1,\ldots,-x_{\ell-1},y_1,\ldots,y_{\ell-1})\rvert\\ &\leq 2\xi^{\ell-1}+2^{\ell-1}\varepsilon_{\ell}^{\ell}\tilde{c}_{\ell}(||x||^{\ell}+||y||^{\ell})\\ &\leq 2\xi^{\ell-1}+2^{\ell-1}\varepsilon_{\ell}^{\ell}\tilde{c}_{\ell}\cdot2 \leq 2^{\ell}, \nonumber \end{align*}$$
which concludes the proof.
Definition 4.3. For any
![]() $x\in \mathbb {G}$
and any
$x\in \mathbb {G}$
and any
![]() $r>0$
, we define
$r>0$
, we define
![]() $G(x,r):=x*\delta _r(G(0,1))$
.
$G(x,r):=x*\delta _r(G(0,1))$
.
Before passing to the proof of our main theorem, a technical result is needed: it quantifies how far
![]() $G(0,1)$
is far from
$G(0,1)$
is far from
![]() $B(0,1)$
, in the sense that
$B(0,1)$
, in the sense that
![]() $G(0,1)\backslash B(0,1)$
contains large balls.
$G(0,1)\backslash B(0,1)$
contains large balls.
Proposition 4.4. Define the functions
![]() $r, s:\mathbb {G}\to (0,+\infty )$
by
$r, s:\mathbb {G}\to (0,+\infty )$
by
 $$\begin{align*}r(x):=\max\Big\{\frac{\lVert x \lVert+\lvert x_1\rvert}{2}, \lVert x\rVert \Big(\frac{(1+10^{-1})(1+2^{\ell}\varepsilon_{\ell}^{\ell} c_{\ell})}{\xi^{\ell-1}}\Big )^{1/\ell} \text{ for } \ell = 2,\dots, \kappa \Big\}, \end{align*}$$
$$\begin{align*}r(x):=\max\Big\{\frac{\lVert x \lVert+\lvert x_1\rvert}{2}, \lVert x\rVert \Big(\frac{(1+10^{-1})(1+2^{\ell}\varepsilon_{\ell}^{\ell} c_{\ell})}{\xi^{\ell-1}}\Big )^{1/\ell} \text{ for } \ell = 2,\dots, \kappa \Big\}, \end{align*}$$
and
Then if
![]() $x\in \mathbb {G}$
satisfies
$x\in \mathbb {G}$
satisfies
![]() $|x_1|<||x||$
, there holds
$|x_1|<||x||$
, there holds
Proof. By homogeneity of the statement, it suffices to handle the case
![]() $\lVert x\rVert =1$
. Fix
$\lVert x\rVert =1$
. Fix
![]() $x\in \mathbb {G}$
with
$x\in \mathbb {G}$
with
![]() $||x||=1$
and
$||x||=1$
and
![]() $|x_1|<1$
. Notice that by (4.2),
$|x_1|<1$
. Notice that by (4.2),
![]() $r(x) < \lVert x \lVert $
and
$r(x) < \lVert x \lVert $
and
![]() $0<s(x)<10^{-1}$
. For
$0<s(x)<10^{-1}$
. For
![]() $y\in B(x,s(x))$
, there holds
$y\in B(x,s(x))$
, there holds
so that
![]() $y\notin B(0,r(x))$
. On the other hand, we claim that
$y\notin B(0,r(x))$
. On the other hand, we claim that
![]() $y\in G(0,r(x))$
, let us prove this layer by layer. Clearly
$y\in G(0,r(x))$
, let us prove this layer by layer. Clearly
Now consider a layer
![]() $\ell \ge 2$
, there holds
$\ell \ge 2$
, there holds
 $$ \begin{align*} \varepsilon_{\ell}^{\ell}\lvert y_{\ell}\lvert &\le \epsilon_{\ell}^{\ell} \lvert x_{\ell} \lvert + s(x)^{\ell} + 2^{\ell-1}\varepsilon_{\ell}^{\ell}\tilde{c}_{\ell}(||x||^{\ell}+s(x)^{\ell}) \\ &\le 1 + s(x)^{\ell} + 2^{\ell-1}\varepsilon_{\ell}^{\ell}\tilde{c}_{\ell}(1+s(x)^{\ell}) \\ &\le (1+ 2^{\ell-1}\varepsilon_{\ell}^{\ell} \tilde{c}_{\ell})(1+s(x)^{\ell}). \end{align*} $$
$$ \begin{align*} \varepsilon_{\ell}^{\ell}\lvert y_{\ell}\lvert &\le \epsilon_{\ell}^{\ell} \lvert x_{\ell} \lvert + s(x)^{\ell} + 2^{\ell-1}\varepsilon_{\ell}^{\ell}\tilde{c}_{\ell}(||x||^{\ell}+s(x)^{\ell}) \\ &\le 1 + s(x)^{\ell} + 2^{\ell-1}\varepsilon_{\ell}^{\ell}\tilde{c}_{\ell}(1+s(x)^{\ell}) \\ &\le (1+ 2^{\ell-1}\varepsilon_{\ell}^{\ell} \tilde{c}_{\ell})(1+s(x)^{\ell}). \end{align*} $$
Recalling the definition of
![]() $r(x)$
, we have
$r(x)$
, we have
Proposition 4.5. Let
![]() $0<\varepsilon <1$
. Assume E is a set in
$0<\varepsilon <1$
. Assume E is a set in
![]() $\mathbb {G}$
, such that
$\mathbb {G}$
, such that
Then, there exists a continuous function
![]() $\varphi :\pi _1(E)\to \mathbb {G}$
, such that
$\varphi :\pi _1(E)\to \mathbb {G}$
, such that
![]() $\varphi (\pi _1\vert _E)=\mathrm {Id}$
on E and that for any
$\varphi (\pi _1\vert _E)=\mathrm {Id}$
on E and that for any
![]() $a,b\in \pi _1(E)$
, we have
$a,b\in \pi _1(E)$
, we have
Proof. First, note that the projection
![]() $\pi _1$
is injective on E. To see this, pick two points
$\pi _1$
is injective on E. To see this, pick two points
![]() $x,y\in E$
, thanks to (4.5), there holds
$x,y\in E$
, thanks to (4.5), there holds
Thus,
![]() $\pi _1$
has an inverse on its image, denote it by
$\pi _1$
has an inverse on its image, denote it by
![]() $\varphi $
. Estimate (4.6) follows from (4.7).
$\varphi $
. Estimate (4.6) follows from (4.7).
Remark 4.6. By definition of r and s, it is clear that given positive parameters
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\alpha>0$
, there exists a
$\alpha>0$
, there exists a
![]() $k=k(\varepsilon ,\alpha )\in \mathbb {N}$
, such that if
$k=k(\varepsilon ,\alpha )\in \mathbb {N}$
, such that if
![]() $s(x)^{\alpha } \le 2 \lVert x\lVert ^{\alpha }/(k-1)$
for some
$s(x)^{\alpha } \le 2 \lVert x\lVert ^{\alpha }/(k-1)$
for some
![]() $x \in \mathbb {G}$
, then
$x \in \mathbb {G}$
, then
![]() $\lvert x_1\rvert \geq (1-\varepsilon )\lVert x\lVert $
.
$\lvert x_1\rvert \geq (1-\varepsilon )\lVert x\lVert $
.
With these tools at hand, we can now state and prove the main step in the proof of Theorem 1.3:
Proposition 4.7. Fix
![]() $\alpha , \varepsilon>0$
, and choose
$\alpha , \varepsilon>0$
, and choose
![]() $k=k(\varepsilon ,\alpha )\geq 2$
as in Remark 4.6. Let E be a Borel set, such that
$k=k(\varepsilon ,\alpha )\geq 2$
as in Remark 4.6. Let E be a Borel set, such that
For each
![]() $j\in \mathbb {N}$
, let
$j\in \mathbb {N}$
, let
![]() $E_{j,k}$
be the set of those
$E_{j,k}$
be the set of those
![]() $x\in E$
, such that
$x\in E$
, such that
Then
![]() $\mathscr {H}^{\alpha }(E\setminus \cup _{j\in \mathbb {N}}E_{j,k})=0$
and the set
$\mathscr {H}^{\alpha }(E\setminus \cup _{j\in \mathbb {N}}E_{j,k})=0$
and the set
![]() $E_{j,k}$
can be covered by images of
$E_{j,k}$
can be covered by images of
![]() $(1-\varepsilon )^{-1}$
-biLipschitz maps from a subset of
$(1-\varepsilon )^{-1}$
-biLipschitz maps from a subset of
![]() $V_1$
endowed with the euclidean metric to
$V_1$
endowed with the euclidean metric to
![]() $\mathbb {G}$
.
$\mathbb {G}$
.
Proof. By Propositions 2.5 and 4.2 and the properties of E for any
![]() $k\in \mathbb {N}$
, we have
$k\in \mathbb {N}$
, we have
![]() $\mathscr {H}^{\alpha }(E\setminus \cup _{j\in \mathbb {N}}E_{j,k})=0$
. Fix two indices
$\mathscr {H}^{\alpha }(E\setminus \cup _{j\in \mathbb {N}}E_{j,k})=0$
. Fix two indices
![]() $j,k\in \mathbb {N}$
and cover
$j,k\in \mathbb {N}$
and cover
![]() $E_{j,k}$
by countably many balls
$E_{j,k}$
by countably many balls
![]() $B(z_i,r_i)$
with
$B(z_i,r_i)$
with
![]() $r_i<(10j)^{-1}$
. For
$r_i<(10j)^{-1}$
. For
![]() $i\in \mathbb {N}$
, we will show that
$i\in \mathbb {N}$
, we will show that
![]() $E_{j,k}\cap B(z_i,r_i)$
is the image of a
$E_{j,k}\cap B(z_i,r_i)$
is the image of a
![]() $1$
-bi-Lipschitz map from a subset of the vector space
$1$
-bi-Lipschitz map from a subset of the vector space
![]() $V_1$
endowed with the Euclidean metric to
$V_1$
endowed with the Euclidean metric to
![]() $\mathbb {G}$
.
$\mathbb {G}$
.
Let
![]() $x,y\in E_{j,k}\cap B(z_i,r_i)$
and without loss of generality, since left translations are isometries, suppose that
$x,y\in E_{j,k}\cap B(z_i,r_i)$
and without loss of generality, since left translations are isometries, suppose that
![]() $x=0$
. Suppose that
$x=0$
. Suppose that
![]() $|y_1|<||y||$
. By Proposition 4.4, we know that
$|y_1|<||y||$
. By Proposition 4.4, we know that
![]() $B(y,s(y))\subset G(0,r)\backslash B(0,r)$
for some
$B(y,s(y))\subset G(0,r)\backslash B(0,r)$
for some
![]() $r\le ||y||<(10j)^{-1}$
. However, by definition of
$r\le ||y||<(10j)^{-1}$
. However, by definition of
![]() $E_{j,k}$
, there holds
$E_{j,k}$
, there holds
and
since
![]() $s(y)<||y||\leq (10j)^{-1}$
. In particular, combining (4.9) and (4.10) and the choice of r, we infer that
$s(y)<||y||\leq (10j)^{-1}$
. In particular, combining (4.9) and (4.10) and the choice of r, we infer that
 $$ \begin{align} \begin{aligned} \Big(1-\frac{1}{k}\Big)\Big (\dfrac{s(y)}{\lVert y \lVert}\Big)^{\alpha} &\le \frac{\mathscr{H}^{\alpha}\llcorner E(B(y,s(y)))}{(2\lVert y\rVert)^{\alpha}}\\[3pt] &\leq \frac{\mathscr{H}^{\alpha}\llcorner E(G(0,r)\backslash B(0,r))}{(2\lVert y\rVert)^{\alpha}}\leq \frac{2k^{-1}(2r)^{\alpha}}{(2\lVert y\rVert)^{\alpha}}\leq 2 k^{-1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \Big(1-\frac{1}{k}\Big)\Big (\dfrac{s(y)}{\lVert y \lVert}\Big)^{\alpha} &\le \frac{\mathscr{H}^{\alpha}\llcorner E(B(y,s(y)))}{(2\lVert y\rVert)^{\alpha}}\\[3pt] &\leq \frac{\mathscr{H}^{\alpha}\llcorner E(G(0,r)\backslash B(0,r))}{(2\lVert y\rVert)^{\alpha}}\leq \frac{2k^{-1}(2r)^{\alpha}}{(2\lVert y\rVert)^{\alpha}}\leq 2 k^{-1}. \end{aligned} \end{align} $$
By the choice of k and Remark 4.6, we conclude that for
![]() $i\in \mathbb {N}$
and
$i\in \mathbb {N}$
and
![]() $x,y\in B(z_i,r_i)\cap E_{j,k}$
, we have
$x,y\in B(z_i,r_i)\cap E_{j,k}$
, we have
and Proposition 4.5 concludes the proof.
Proof of Theorem 1.3.
As
![]() $\pi _1$
is 1-Lipschitz,
$\pi _1$
is 1-Lipschitz,
![]() $\pi _1(E)$
has
$\pi _1(E)$
has
![]() $\sigma $
-finite Hausdorff measure, in particular, it has upper Hausdorff density at most
$\sigma $
-finite Hausdorff measure, in particular, it has upper Hausdorff density at most
![]() $1$
,
$1$
,
![]() $\mathscr {H}^{\alpha }$
-almost everywhere. Fix
$\mathscr {H}^{\alpha }$
-almost everywhere. Fix
![]() $\eta>0$
, by Proposition 4.7, for every
$\eta>0$
, by Proposition 4.7, for every
![]() $\eta>0$
, E can be covered up to an
$\eta>0$
, E can be covered up to an
![]() $\mathscr {H}^{\alpha }$
-null set by countably many images of
$\mathscr {H}^{\alpha }$
-null set by countably many images of
![]() $(1+\eta )$
-biLipschitz maps
$(1+\eta )$
-biLipschitz maps
![]() $f_n^{\eta }$
defined on subsets
$f_n^{\eta }$
defined on subsets
![]() $A_n^{\eta }$
of
$A_n^{\eta }$
of
![]() $V_1$
. As E has unit Hausdorff density
$V_1$
. As E has unit Hausdorff density
![]() $\mathscr {H}^{\alpha }$
-almost everywhere, so do its subsets
$\mathscr {H}^{\alpha }$
-almost everywhere, so do its subsets
![]() $f_n^{\eta }(A_n^{\eta })$
at almost every point (see, for instance, [Reference Antonelli and Merlo2, Proposition 2.2]). Pick such a point
$f_n^{\eta }(A_n^{\eta })$
at almost every point (see, for instance, [Reference Antonelli and Merlo2, Proposition 2.2]). Pick such a point
![]() $x\in f_n^{\eta }(A_n^{\eta })$
. Writing
$x\in f_n^{\eta }(A_n^{\eta })$
. Writing
![]() $f:= f_n^{\eta }$
and
$f:= f_n^{\eta }$
and
![]() $A:= A_n^{\eta }$
for simplicity, there holds
$A:= A_n^{\eta }$
for simplicity, there holds
On the one hand, since
![]() $\pi _1$
is
$\pi _1$
is
![]() $1$
-Lipschitz, there holds
$1$
-Lipschitz, there holds
and on the other hand, as f is
![]() $(1+\eta )$
-Lipschitz, we have
$(1+\eta )$
-Lipschitz, we have
This implies
Letting r go to
![]() $0$
, we obtain a bound on the lower density of
$0$
, we obtain a bound on the lower density of
![]() $\pi _1(E)$
:
$\pi _1(E)$
:
Thus, for every
![]() $\eta>0$
, there is a subset of
$\eta>0$
, there is a subset of
![]() $\pi _1(E)$
of full
$\pi _1(E)$
of full
![]() $\mathscr {H}^{\alpha }$
-measure with lower Hausdorff density at least
$\mathscr {H}^{\alpha }$
-measure with lower Hausdorff density at least
![]() $(1+\eta )^{-\alpha }$
. Taking a countable intersection for a sequence of parameters
$(1+\eta )^{-\alpha }$
. Taking a countable intersection for a sequence of parameters
![]() $\eta $
going to zero yields a subset of
$\eta $
going to zero yields a subset of
![]() $\pi _1(E)$
of full measure with unit Hausdorff density. Note that the Hausdorff measure and the density on
$\pi _1(E)$
of full measure with unit Hausdorff density. Note that the Hausdorff measure and the density on
![]() $V_1$
are computed with respect to the euclidean norm. By Marstrand’s Theorem (see [Reference De Lellis8, Theorem 3.1], we have
$V_1$
are computed with respect to the euclidean norm. By Marstrand’s Theorem (see [Reference De Lellis8, Theorem 3.1], we have
![]() $\alpha \in \{1,\ldots ,n_1\}$
. Therefore, the main result of [Reference Mattila22] applies and
$\alpha \in \{1,\ldots ,n_1\}$
. Therefore, the main result of [Reference Mattila22] applies and
![]() $\pi _1(E)$
is euclidean rectifiable. Using the biLipschitz maps of Proposition 4.7, one therefore sees that E itself is
$\pi _1(E)$
is euclidean rectifiable. Using the biLipschitz maps of Proposition 4.7, one therefore sees that E itself is
![]() $\alpha $
-rectifiable (in the metric sense of Federer, see [Reference Federer9, Section 3.2.14]). In addition, by the Pansu-Rademacher Theorem, it is possible to show that the tangent measures of
$\alpha $
-rectifiable (in the metric sense of Federer, see [Reference Federer9, Section 3.2.14]). In addition, by the Pansu-Rademacher Theorem, it is possible to show that the tangent measures of
![]() $\mathscr {H}^{\alpha }\llcorner E$
must be almost everywhere the Haar measure of some subgroup of
$\mathscr {H}^{\alpha }\llcorner E$
must be almost everywhere the Haar measure of some subgroup of
![]() $V_1$
, and hence,
$V_1$
, and hence,
![]() $\alpha $
must be the dimension of one of those horizontal subgroups.
$\alpha $
must be the dimension of one of those horizontal subgroups.
5 The case of metric Lie groups admitting dilations
In this section, we discuss metric Lie groups admitting dilations, and show that they are not too different from homogeneous groups, in the sense that they admit biLipschitz equivalent ‘homogeneous’ distances for which Theorem 1.2 holds, with the same proof as above.
Definition 5.1. If
![]() $\mathbb {G}$
is a Lie group with Lie algebra
$\mathbb {G}$
is a Lie group with Lie algebra
![]() $\mathfrak {g}$
, a linear map
$\mathfrak {g}$
, a linear map
![]() $A:\mathfrak {g}\to \mathfrak {g}$
is a derivation if it obeys the Leibniz law
$A:\mathfrak {g}\to \mathfrak {g}$
is a derivation if it obeys the Leibniz law
![]() $A([x,y])= [A(x),y] + [x, A(y)]$
. A derivation determines a one parameter family of dilations
$A([x,y])= [A(x),y] + [x, A(y)]$
. A derivation determines a one parameter family of dilations
![]() $(0,+\infty )\to \mathrm {Aut}(\mathbb {G})$
:
$(0,+\infty )\to \mathrm {Aut}(\mathbb {G})$
:
A left-invariant distance d on
![]() $\mathbb {G}$
is A-homogeneous if for every
$\mathbb {G}$
is A-homogeneous if for every
![]() $\lambda \in (0,\infty )$
, we have
$\lambda \in (0,\infty )$
, we have
![]() $d(\delta _{\lambda } x,\delta _{\lambda } y )=\lambda d(x,y)$
.
$d(\delta _{\lambda } x,\delta _{\lambda } y )=\lambda d(x,y)$
.
Note that if A is diagonalisable in
![]() $\mathbb {R}$
with integer eigenvalues, then
$\mathbb {R}$
with integer eigenvalues, then
![]() $\mathbb {G}$
admits an A-homogeneous distance and is in fact a homogeneous group. If A is diagonalisable in
$\mathbb {G}$
admits an A-homogeneous distance and is in fact a homogeneous group. If A is diagonalisable in
![]() $\mathbb {R}$
, but not all eigenvalues are integers, we can construct an equivalent homogeneous distance on
$\mathbb {R}$
, but not all eigenvalues are integers, we can construct an equivalent homogeneous distance on
![]() $\mathbb {G}$
, such that the results of the previous section apply. This is relevant because combining Theorem 1.2, Corollary 2.6 and Lemma 6.1 from [Reference Le Donne and Golo17], yields the following:
$\mathbb {G}$
, such that the results of the previous section apply. This is relevant because combining Theorem 1.2, Corollary 2.6 and Lemma 6.1 from [Reference Le Donne and Golo17], yields the following:
Proposition 5.2. A Lie group endowed with an A-homogeneous distance for some derivation A of its Lie algebra is biLipschitz equivalent to a Lie group with an A-homogeneous distance, where A has real spectrum
![]() $1\leq t_1\leq \dots \leq t_{\kappa } <\infty $
. Moreover, denoting by
$1\leq t_1\leq \dots \leq t_{\kappa } <\infty $
. Moreover, denoting by
![]() $V_{t_j}$
the eigenspaces of A,
$V_{t_j}$
the eigenspaces of A,
![]() $A|_{V_1}$
is diagonalisable.
$A|_{V_1}$
is diagonalisable.
The authors of [Reference Le Donne and Golo17] construct an A-homogeneous distance on such groups, which is similar to the Koranyi norm. It is more convenient for us to define a smooth-box distance instead. The following statement contains the properties of this distance, which suffice to prove an analogue of Theorem 1.2.
Theorem 5.3. If
![]() $(\mathbb {G},A)$
is a Lie group endowed with an A-homogeneous distance for some derivation A of its Lie algebra, then
$(\mathbb {G},A)$
is a Lie group endowed with an A-homogeneous distance for some derivation A of its Lie algebra, then
-
(i) for each j, there exists an A-homogeneous distance
 $||\cdot ||$
on
$||\cdot ||$
on
 $\mathbb {G}$
defined by (5.1)where
$\mathbb {G}$
defined by (5.1)where $$ \begin{align} || (x_{t_1},\dots , x_{t_{\kappa}})|| := \max \{ \varepsilon_{t_j} ||x_{t_j}||_{V_{t_j}}^{1/t_j}, j=1,\dots, \kappa\}, \end{align} $$
$$ \begin{align} || (x_{t_1},\dots , x_{t_{\kappa}})|| := \max \{ \varepsilon_{t_j} ||x_{t_j}||_{V_{t_j}}^{1/t_j}, j=1,\dots, \kappa\}, \end{align} $$
 $\varepsilon _{t_1}= 1$
if
$\varepsilon _{t_1}= 1$
if
 $V_{t_1}\neq \{0\}$
and the other
$V_{t_1}\neq \{0\}$
and the other
 $\varepsilon _{t_j}$
are chosen suitably small with respect to the coefficients of the expression for the operation given by the Baker-Campbell-Hausdorff formula. Here, the norms
$\varepsilon _{t_j}$
are chosen suitably small with respect to the coefficients of the expression for the operation given by the Baker-Campbell-Hausdorff formula. Here, the norms
 $\lVert \cdot \rVert _{V_{t_j}}$
can be taken to be the euclidean norm on
$\lVert \cdot \rVert _{V_{t_j}}$
can be taken to be the euclidean norm on
 $V_{t_j}$
.
$V_{t_j}$
.
-
(ii) The projection
 $\pi _1:x\mapsto x_{t_1} \in V_{t_1}$
is
$\pi _1:x\mapsto x_{t_1} \in V_{t_1}$
is
 $1$
-Lipschitz continuous.
$1$
-Lipschitz continuous. -
(iii) If
 $B(x,r)$
denotes the balls relative to the norm
$B(x,r)$
denotes the balls relative to the norm
 $||\cdot ||$
, one can define
$||\cdot ||$
, one can define
 $G(0,1)$
in much the same way as Proposition 4.2 and one has
$G(0,1)$
in much the same way as Proposition 4.2 and one has
 $G(0,1)\supset B(0,1)$
as in Definition 4.3, and
$G(0,1)\supset B(0,1)$
as in Definition 4.3, and
 $G(0,1)$
has diameter
$G(0,1)$
has diameter
 $2$
.
$2$
.
Proof. The proof of (i) is a modification of that of [Reference Le Donne and Golo17, Theorem 1.2]. One first choses a basis of
![]() $\mathfrak {g}$
in which A is in Jordan normal form. Considering the spaces
$\mathfrak {g}$
in which A is in Jordan normal form. Considering the spaces
![]() $V_{t_j}$
one by one and rescaling their bases yields an euclidean norm on each
$V_{t_j}$
one by one and rescaling their bases yields an euclidean norm on each
![]() $V_{t_j}$
, such that for
$V_{t_j}$
, such that for
![]() $\lambda \in (0,1\,]$
, the operator norm of
$\lambda \in (0,1\,]$
, the operator norm of
![]() $\lambda ^{A}|_{V_{t_j}}$
is bounded from above by
$\lambda ^{A}|_{V_{t_j}}$
is bounded from above by
![]() $\lambda ^{t_j-\theta _j}$
for a
$\lambda ^{t_j-\theta _j}$
for a
![]() $\theta _j>0$
, which can be chosen arbitrarily small. As
$\theta _j>0$
, which can be chosen arbitrarily small. As
![]() $A|_{V_1}$
is diagonalisable in
$A|_{V_1}$
is diagonalisable in
![]() $\mathbb {R}$
, with eigenvalues at least
$\mathbb {R}$
, with eigenvalues at least
![]() $1$
, the operator norm of
$1$
, the operator norm of
![]() $\lambda ^{A}|_{V_1}$
is necessarily
$\lambda ^{A}|_{V_1}$
is necessarily
![]() $\lambda $
. Writing
$\lambda $
. Writing
![]() $||\cdot ||$
as in (5.1), it suffices to prove that the ‘unit ball’
$||\cdot ||$
as in (5.1), it suffices to prove that the ‘unit ball’
![]() $B:=\{x,||x||\le 1\}$
is A-convexFootnote
1
, that is, for
$B:=\{x,||x||\le 1\}$
is A-convexFootnote
1
, that is, for
![]() $\lambda \in (0,1)$
and
$\lambda \in (0,1)$
and
![]() $x,y$
in B, there holds
$x,y$
in B, there holds
This is done iteratively over the subspaces
![]() $V_{t_j}$
. For
$V_{t_j}$
. For
![]() $V_1$
it is clear. For
$V_1$
it is clear. For
![]() $V_{t_j}$
with
$V_{t_j}$
with
![]() $1<t_j<2$
, one proceeds as in Lemma 6.5 of [Reference Le Donne and Golo17] (the key remark being that the components of all commutators vanish in the layers of order less than
$1<t_j<2$
, one proceeds as in Lemma 6.5 of [Reference Le Donne and Golo17] (the key remark being that the components of all commutators vanish in the layers of order less than
![]() $2$
). For
$2$
). For
![]() $t_j=2$
, the reasoning of Lemma 6.7 in [Reference Le Donne and Golo17] works: for
$t_j=2$
, the reasoning of Lemma 6.7 in [Reference Le Donne and Golo17] works: for
![]() $x,y\in \mathbb {G}$
and
$x,y\in \mathbb {G}$
and
![]() $\lambda \in (0,1)$
, by the Baker-Campbell-Hausdorff formula, there holds
$\lambda \in (0,1)$
, by the Baker-Campbell-Hausdorff formula, there holds
So that
 $$ \begin{align*} \begin{aligned} \Vert ((\lambda^A x) \cdot ((1-\lambda)^Ay))_2\Vert_2 \le & \\ \lambda^2 (\Vert x_2 \Vert_2+ f(\lambda)) &+ (1-\lambda)^2 (\Vert y_2\Vert_2 + f(1-\lambda))+ C \lambda(1-\lambda) \Vert x_1\Vert_1 \Vert y_1\Vert_1, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \Vert ((\lambda^A x) \cdot ((1-\lambda)^Ay))_2\Vert_2 \le & \\ \lambda^2 (\Vert x_2 \Vert_2+ f(\lambda)) &+ (1-\lambda)^2 (\Vert y_2\Vert_2 + f(1-\lambda))+ C \lambda(1-\lambda) \Vert x_1\Vert_1 \Vert y_1\Vert_1, \end{aligned} \end{align*} $$
where f is an error term coming from the dilations and is subpolynomial in
![]() $|\log \lambda |$
. The whole controlled by a constant independent of
$|\log \lambda |$
. The whole controlled by a constant independent of
![]() $x,y$
. It then suffices to take
$x,y$
. It then suffices to take
![]() $\varepsilon _2$
small enough.
$\varepsilon _2$
small enough.
For
![]() $t_j>2$
, one needs to use the Baker-Campbell-Hausdorff formula, as in the proof that the smooth-box norm on a Carnot group is a metric (see the appendix of [Reference Franchi, Serapioni and Serra Cassano11]), but as for
$t_j>2$
, one needs to use the Baker-Campbell-Hausdorff formula, as in the proof that the smooth-box norm on a Carnot group is a metric (see the appendix of [Reference Franchi, Serapioni and Serra Cassano11]), but as for
![]() $t_j=2$
, it is slightly more subtle (see Proposition 6.8 in [Reference Le Donne and Golo17]).
$t_j=2$
, it is slightly more subtle (see Proposition 6.8 in [Reference Le Donne and Golo17]).
In order to prove (ii), pick
![]() $x= (x_1,x_{t_2},\dots , x_{t_{\kappa }})\in \mathbb {G}$
. It suffices to note that on the one hand
$x= (x_1,x_{t_2},\dots , x_{t_{\kappa }})\in \mathbb {G}$
. It suffices to note that on the one hand
which follows from convexity, and on the other hand, that iterating the procedure yields a sequence which tends to
![]() $(x_1,0,\dots )$
as in Proposition 2.2. The fact that the components of order
$(x_1,0,\dots )$
as in Proposition 2.2. The fact that the components of order
![]() $t_j>1$
tend to
$t_j>1$
tend to
![]() $0$
is a consequence of
$0$
is a consequence of
![]() $2 (1/2)^{t_j} <1$
. And the fact that the first component remains constant is clear because
$2 (1/2)^{t_j} <1$
. And the fact that the first component remains constant is clear because
![]() $A|_{V_1}$
is diagonalisable over
$A|_{V_1}$
is diagonalisable over
![]() $\mathbb {R}$
with eigenvalues
$\mathbb {R}$
with eigenvalues
![]() $1$
(in fact, it is the identity). The proof of (iii) is straightforward using the properties of
$1$
(in fact, it is the identity). The proof of (iii) is straightforward using the properties of
![]() $||\cdot ||$
and the method of the previous section.
$||\cdot ||$
and the method of the previous section.
Corollary 5.4. Suppose
![]() $\mathbb {G}$
is a Lie group endowed with an A-homogeneous distance for some derivation A of its Lie algebra. Then, there exists a biLipschitz equivalent A-homogeneous distance
$\mathbb {G}$
is a Lie group endowed with an A-homogeneous distance for some derivation A of its Lie algebra. Then, there exists a biLipschitz equivalent A-homogeneous distance
![]() $\lVert \cdot \rVert $
on
$\lVert \cdot \rVert $
on
![]() $\mathbb {G}$
, such that the following holds. Whenever
$\mathbb {G}$
, such that the following holds. Whenever
![]() $\alpha \ge 0$
and
$\alpha \ge 0$
and
![]() $E\subset \mathbb {G}$
is a Borel set for which
$E\subset \mathbb {G}$
is a Borel set for which
![]() $\Theta ^{\alpha }(E,x)=1$
for
$\Theta ^{\alpha }(E,x)=1$
for
![]() $\mathscr {H}^{\alpha }$
-almost every
$\mathscr {H}^{\alpha }$
-almost every
![]() $x\in E$
, then
$x\in E$
, then
![]() $\alpha $
is not larger than the dimension of the first layer of the Lie algebra of
$\alpha $
is not larger than the dimension of the first layer of the Lie algebra of
![]() $\mathbb {G}$
,
$\mathbb {G}$
,
![]() $\alpha $
is an integer and E is
$\alpha $
is an integer and E is
![]() $\alpha $
-rectifiable.
$\alpha $
-rectifiable.
6 Discussion of the results in the first Heisenberg group
The point of this section is to compare the results of this work with the existing literature in the particular case of the first Heisenberg group. The group law of
![]() $\mathbb {H}^1$
is given by
$\mathbb {H}^1$
is given by
where J is the standard symplectic
![]() $2\times 2$
matrix. Throughout this section, we will endow
$2\times 2$
matrix. Throughout this section, we will endow
![]() $\mathbb {H}^1$
with the Koranyi metric, which is the following homogeneous left-invariant distance
$\mathbb {H}^1$
with the Koranyi metric, which is the following homogeneous left-invariant distance
The fact that this formula defines a distance was first proved in [Reference Cygan7].
Before delving into the discussion, we recall that whenever we endow
![]() $\mathbb {H}^1$
with a left-invariant and homogeneous metric d, the metric space
$\mathbb {H}^1$
with a left-invariant and homogeneous metric d, the metric space
![]() $(\mathbb {H}^1,d)$
is a
$(\mathbb {H}^1,d)$
is a
![]() $2,3,4$
-purely unrectifiable metric space of Hausdorff dimension
$2,3,4$
-purely unrectifiable metric space of Hausdorff dimension
![]() $4$
(see [Reference Kirchheim and Preiss14]). Another property of the Koranyi metric is that its ball, like that of the smooth-box metric, is not isodiametric (see [Reference Rigot30, Theorem 3.5] and [Reference Schechter31, Theorem 38]).
$4$
(see [Reference Kirchheim and Preiss14]). Another property of the Koranyi metric is that its ball, like that of the smooth-box metric, is not isodiametric (see [Reference Rigot30, Theorem 3.5] and [Reference Schechter31, Theorem 38]).
Proposition 6.1. Let
![]() $G(0,1)$
be the subset of those
$G(0,1)$
be the subset of those
![]() $x=(x_1,x_2)\in \mathbb {H}^1$
, such that
$x=(x_1,x_2)\in \mathbb {H}^1$
, such that
Then
![]() $B(0,1)\subsetneq G(0,1)$
and
$B(0,1)\subsetneq G(0,1)$
and
![]() $\mathrm {diam}(G(0,1))\leq 2$
.
$\mathrm {diam}(G(0,1))\leq 2$
.
Remark 6.2. The proof follows the argument of Cygan’s proof of the subadditivity of the Koranyi norm [Reference Cygan7]. In particular, it works in any H-type group endowed with the gauge distance.
Proof. Let
![]() $p:=(x_1,x_2)$
and
$p:=(x_1,x_2)$
and
![]() $p':=(x^{\prime }_1, x^{\prime }_2)$
be points of
$p':=(x^{\prime }_1, x^{\prime }_2)$
be points of
![]() $G(0,1)$
. Using the symmetry of G, and to avoid annoying signs, we compute the distance between
$G(0,1)$
. Using the symmetry of G, and to avoid annoying signs, we compute the distance between
![]() $p^{-1}$
and
$p^{-1}$
and
![]() $p'$
, we can write
$p'$
, we can write
 $$ \begin{align*} \lVert p*p'\rVert^4 &= (|x_1|^2 + |x^{\prime}_1|^2 + 2 \langle x_1, x^{\prime}_1 \rangle)^2 + (x_2 + x^{\prime}_2 + 2 \langle x_1, J x^{\prime}_1\rangle)^2\\&= |x_1|^4 + |x^{\prime}_1|^4 + 4 \langle x_1,x^{\prime}_1\rangle^2 + 4 (|x_1|^2 + |x_2|^2)\langle x_1,x^{\prime}_1\rangle + 2 |x_1|^2 |x^{\prime}_1|^2\\& \quad + |x_2|^2 + |x^{\prime}_2|^2 + 4 \langle x_1, J x^{\prime}_1 \rangle^2 + 4 (x_2+x^{\prime}_2) \langle x_1,J x^{\prime}_1\rangle + 2 x_2 x^{\prime}_2\\&= (|x_1|^4 + |x_2|^2 ) + (|x^{\prime}_1|^4 + |x^{\prime}_2|^2) \\& \quad + 2 |x_1|^2|x^{\prime}_1|^2 + 2 x_2x^{\prime}_2\\& \quad + 4 \langle x_1,x^{\prime}_1\rangle^2 + 4\langle x_1, J x^{\prime}_1 \rangle^2\\& \quad + 4 |x_1|^2 \langle x_1,x^{\prime}_1\rangle + 4 x_2 \langle x_1,J x^{\prime}_1\rangle\\& \quad + 4 |x^{\prime}_1|^2 \langle x_1,x^{\prime}_1\rangle + 4 x^{\prime}_2 \langle x_1,J x^{\prime}_1\rangle. \end{align*} $$
$$ \begin{align*} \lVert p*p'\rVert^4 &= (|x_1|^2 + |x^{\prime}_1|^2 + 2 \langle x_1, x^{\prime}_1 \rangle)^2 + (x_2 + x^{\prime}_2 + 2 \langle x_1, J x^{\prime}_1\rangle)^2\\&= |x_1|^4 + |x^{\prime}_1|^4 + 4 \langle x_1,x^{\prime}_1\rangle^2 + 4 (|x_1|^2 + |x_2|^2)\langle x_1,x^{\prime}_1\rangle + 2 |x_1|^2 |x^{\prime}_1|^2\\& \quad + |x_2|^2 + |x^{\prime}_2|^2 + 4 \langle x_1, J x^{\prime}_1 \rangle^2 + 4 (x_2+x^{\prime}_2) \langle x_1,J x^{\prime}_1\rangle + 2 x_2 x^{\prime}_2\\&= (|x_1|^4 + |x_2|^2 ) + (|x^{\prime}_1|^4 + |x^{\prime}_2|^2) \\& \quad + 2 |x_1|^2|x^{\prime}_1|^2 + 2 x_2x^{\prime}_2\\& \quad + 4 \langle x_1,x^{\prime}_1\rangle^2 + 4\langle x_1, J x^{\prime}_1 \rangle^2\\& \quad + 4 |x_1|^2 \langle x_1,x^{\prime}_1\rangle + 4 x_2 \langle x_1,J x^{\prime}_1\rangle\\& \quad + 4 |x^{\prime}_1|^2 \langle x_1,x^{\prime}_1\rangle + 4 x^{\prime}_2 \langle x_1,J x^{\prime}_1\rangle. \end{align*} $$
Now we proceed as in [Reference Cygan7], using Cauchy-Schwarz and the inequality
![]() $\langle z,z'\rangle ^2 + \langle z,J z'\rangle ^2 \le |z|^2|z'|^2$
. Noting that
$\langle z,z'\rangle ^2 + \langle z,J z'\rangle ^2 \le |z|^2|z'|^2$
. Noting that
![]() $|x_2|^2\le 2(1-|x_1|^4)$
, we obtain
$|x_2|^2\le 2(1-|x_1|^4)$
, we obtain
 $$ \begin{align*} \lVert p*p'\rVert^4 &\le 4 - |x_1|^4 - |x^{\prime}_1|^4 \\& \quad + 4 |x_1|^2 |x^{\prime}_1|^2 + 2 (2-|x_1|^4)^{1/2}(2-|x^{\prime}_1|^4)^{1/2}\\& \quad + 4 \big ( (2-|x_1|^4)^{1/2} + (2-|x^{\prime}_1|^4)^{1/2} \big ) |x_1| |x^{\prime}_1|. \end{align*} $$
$$ \begin{align*} \lVert p*p'\rVert^4 &\le 4 - |x_1|^4 - |x^{\prime}_1|^4 \\& \quad + 4 |x_1|^2 |x^{\prime}_1|^2 + 2 (2-|x_1|^4)^{1/2}(2-|x^{\prime}_1|^4)^{1/2}\\& \quad + 4 \big ( (2-|x_1|^4)^{1/2} + (2-|x^{\prime}_1|^4)^{1/2} \big ) |x_1| |x^{\prime}_1|. \end{align*} $$
Using Young’s inequality for the terms on the second line yields
We need to show that the whole is smaller than
![]() $16$
, so it suffices to show:
$16$
, so it suffices to show:
Since
![]() $\sqrt {1+s} \le 1+ s/2$
, it suffices that there holds
$\sqrt {1+s} \le 1+ s/2$
, it suffices that there holds
Freezing the variable a, and differentiating, we remark that the maximum is reached at
![]() $b=1$
. So we just need to check that
$b=1$
. So we just need to check that
![]() $(5/2 - a^4/2) a \le 2$
for
$(5/2 - a^4/2) a \le 2$
for
![]() $a\in [\,0,1\,]$
, which we leave to the reader.
$a\in [\,0,1\,]$
, which we leave to the reader.
It is not hard to see that one can then obtain an analogue of Proposition 4.4, taking, for instance,
![]() $r(x) ^4:= |x_1|^4 + \frac 32 |x_2|^2$
and
$r(x) ^4:= |x_1|^4 + \frac 32 |x_2|^2$
and
![]() $s(x)^4 := c^4 |x_2|^2$
, for some
$s(x)^4 := c^4 |x_2|^2$
, for some
![]() $c>0$
small enough. This, in turn, implies that the proof of Theorem 1.3 can be adapted to this setting, and we get:
$c>0$
small enough. This, in turn, implies that the proof of Theorem 1.3 can be adapted to this setting, and we get:
Theorem 6.3. Suppose E is a Borel subset of
![]() $\mathbb {H}^1$
for which there exists an
$\mathbb {H}^1$
for which there exists an
![]() $\alpha>0$
, such that
$\alpha>0$
, such that
and where
![]() $B(x,r)$
is the ball relative to the Koranyi distance (see (6.1)). Then
$B(x,r)$
is the ball relative to the Koranyi distance (see (6.1)). Then
![]() $\alpha =1$
and E can be covered with countably many Lipschitz images of compact subsets of
$\alpha =1$
and E can be covered with countably many Lipschitz images of compact subsets of
![]() $\mathbb {R}$
up to an
$\mathbb {R}$
up to an
![]() $\mathscr {H}^1$
-null set.
$\mathscr {H}^1$
-null set.
Putting together [Reference Kirchheim13] and Theorem 6.3, we obtain, as in Theorem 1.2, that rectifiable sets are characterised by having unit density for the Hausdorff measure almost everywhere. Furthermore, thanks to the work of Antonelli, Chousionis, Magnani, Tyson and the second named author, the density problem, see [Reference Merlo24] for a proper definition, has a complete and satisfactory solution in
![]() $\mathbb {H}^1$
endowed with the Koranyi metric
$\mathbb {H}^1$
endowed with the Koranyi metric
Theorem 6.4 [Reference Antonelli and Merlo3, Reference Chousionis, Magnani and Tyson5, Reference Chousionis and Tyson6, Reference Merlo24, Reference Merlo25].
Let
![]() $\phi $
be a Radon measure on
$\phi $
be a Radon measure on
![]() $(\mathbb {H}^1,d)$
, such that the limit
$(\mathbb {H}^1,d)$
, such that the limit
exists and is positive and finite
![]() $\phi $
-almost everywhere, then
$\phi $
-almost everywhere, then
![]() $\phi \ll \mathscr {H}^{\alpha }$
,
$\phi \ll \mathscr {H}^{\alpha }$
,
![]() $\alpha \in \{0,1,\ldots ,4\}$
and
$\alpha \in \{0,1,\ldots ,4\}$
and
![]() $\phi $
is
$\phi $
is
![]() $\mathscr {P}_{\alpha }$
-rectifiable, or in other words
$\mathscr {P}_{\alpha }$
-rectifiable, or in other words
-
(i) if
 $\alpha =0$
, then
$\alpha =0$
, then
 $\phi $
is a sum of countably many multiples of Dirac masses;
$\phi $
is a sum of countably many multiples of Dirac masses; -
(ii) if
 $\alpha =1$
, then
$\alpha =1$
, then
 $\mathbb {H}^1$
can be covered
$\mathbb {H}^1$
can be covered
 $\phi $
-almost all by countably many Lipschitz images of
$\phi $
-almost all by countably many Lipschitz images of
 $\mathbb {R}$
;
$\mathbb {R}$
; -
(iii) if
 $\alpha =2$
, then
$\alpha =2$
, then
 $\phi $
-almost everywhere the blowups of the measure
$\phi $
-almost everywhere the blowups of the measure
 $\phi $
coincide with the vertical line
$\phi $
coincide with the vertical line
 $\mathscr {V}:=\mathrm {span}\{e_3\}$
, for a precise statement, we refer to the introduction of [Reference Antonelli and Merlo3];
$\mathscr {V}:=\mathrm {span}\{e_3\}$
, for a precise statement, we refer to the introduction of [Reference Antonelli and Merlo3]; -
(iv) if
 $\alpha =3$
, then
$\alpha =3$
, then
 $\mathbb {H}^1$
can be covered up to a
$\mathbb {H}^1$
can be covered up to a
 $\phi $
-null set by countably many
$\phi $
-null set by countably many
 $C^1_{\mathbb {H}^1}$
surfaces (see Definition 3.1).
$C^1_{\mathbb {H}^1}$
surfaces (see Definition 3.1).
For the last point, recall that
![]() $C^1_{\mathbb {H}^1}$
-surfaces, introduced in [Reference Franchi, Serapioni and Serra Cassano10], can be fractals from the euclidean perspective and that at the present time, it is unknown if they are ‘parabolic rectifiable’. This would mean that they can be covered up to a null set by countably many Lipschitz images of compact subsets of the parabolic plane, which is the model for homogeneous
$C^1_{\mathbb {H}^1}$
-surfaces, introduced in [Reference Franchi, Serapioni and Serra Cassano10], can be fractals from the euclidean perspective and that at the present time, it is unknown if they are ‘parabolic rectifiable’. This would mean that they can be covered up to a null set by countably many Lipschitz images of compact subsets of the parabolic plane, which is the model for homogeneous
![]() $1$
-codimensional subgroups of
$1$
-codimensional subgroups of
![]() $\mathbb {H}^1$
.
$\mathbb {H}^1$
.
The above result is the analogue of the celebrated Preiss’ rectifiability theorem, see [Reference Preiss28], in the first Heisenberg group
![]() $\mathbb {H}^1$
. Theorems 6.3 and 6.4 show that there are both great similarities and differences between the general homogeneous groups and euclidean space. On the one hand, the density problem has a natural solution in the form of Theorem 6.4. On the other, Theorem 6.3 tells us that
$\mathbb {H}^1$
. Theorems 6.3 and 6.4 show that there are both great similarities and differences between the general homogeneous groups and euclidean space. On the one hand, the density problem has a natural solution in the form of Theorem 6.4. On the other, Theorem 6.3 tells us that
![]() $C^1_{\mathbb {H}^1}$
-regular surfaces cannot have unit density for the Hausdorff measure. This phenomenon, however, should be expected in view of Theorem 3.4, which tells us that in order to have unit density for the Hausdorff measure at a point for a
$C^1_{\mathbb {H}^1}$
-regular surfaces cannot have unit density for the Hausdorff measure. This phenomenon, however, should be expected in view of Theorem 3.4, which tells us that in order to have unit density for the Hausdorff measure at a point for a
![]() $C^1_{\mathbb {H}^1}$
-surface, we need the intersection of the ball with the tangent plane at that point to be an isodiametric set.
$C^1_{\mathbb {H}^1}$
-surface, we need the intersection of the ball with the tangent plane at that point to be an isodiametric set.
Acknowledgments
A.J. wishes to thank Enrico Le Donne for interesting discussions. This work was completed at the HIM in Bonn during the 2022 Trimester Interactions between geometric measure theory, singular integrals, and partial differential equations. We wish to thank the organisers of this event and the Hausdorff Research Institute for Mathematics (HIM) staff. We also thank the anonymous referees for their comments and corrections. Both A.J. and A.M. were supported by the Simons Foundation grant 601941, GD. A.M. was partially supported by the Swiss National Science Foundation (grant 200021-204501 ‘Regularity of sub-Riemannian geodesics and applications’), by the European Research Council (ERC Starting Grant 713998 GeoMeG ‘Geometry of Metric Groups’) and by the European Union’s Horizon Europe research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 101065346.
Competing interest
The authors have no competing interest to declare.