FirstView articles
Contents
Article
The boundary rigidity for holomorphic self-maps on bounded symmetric domains with an interior fixed point
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2025, pp. 1-4
-
- Article
- Export citation
The
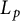 $L_p$ Gauss image problem for C-pseudo-cones
$L_p$ Gauss image problem for C-pseudo-cones
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2025, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Polynomial invariants for three-dimensional Leibniz algebras
- Part of:
-
- Published online by Cambridge University Press:
- 25 November 2025, pp. 1-20
-
- Article
- Export citation
Rational Delsarte designs and Galois fusions of association schemes
- Part of:
-
- Published online by Cambridge University Press:
- 18 November 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Localization operators on discrete Orlicz modulation spaces
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-21
-
- Article
- Export citation
An asymptotic formula for Tate–Shafarevich groups of CM elliptic curves at supersingular primes
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A deformation approach to the BFK formula
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the class of weak U-Dunford–Pettis operators
- Part of:
-
- Published online by Cambridge University Press:
- 12 November 2025, pp. 1-13
-
- Article
- Export citation
Erratum
Steiner Coset Partitions of Groups – ERRATUM
-
- Published online by Cambridge University Press:
- 07 November 2025, p. 1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Article
A remark on characterizing inner product spaces via strong three-point homogeneity
- Part of:
-
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Not every complete lattice can support a unital quantale
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2025, pp. 1-12
-
- Article
- Export citation
Cartan decomposition for
 $\mathrm {Sp}(1,n)$ and some applications to group dynamics
$\mathrm {Sp}(1,n)$ and some applications to group dynamics
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2025, pp. 1-17
-
- Article
- Export citation
Corrigendum
Correction to “Irreducible modules of modular Lie superalgebras and super version of the first Kac-Weisfeiler conjecture”
- Part of:
-
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Article
Perturbed cone theorems for proper harmonic maps
- Part of:
-
- Published online by Cambridge University Press:
- 22 October 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of
 $\mathbb {Q}$-linear maps from
$\mathbb {Q}$-linear maps from  $\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to
$\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to  $\mathbb {R}$
$\mathbb {R}$
- Part of:
-
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical range of Toeplitz and weighted composition operators on weighted Bergman spaces
- Part of:
-
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A short proof of the Hilton–Milner Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral gradient estimates on a closed surface
- Part of:
-
- Published online by Cambridge University Press:
- 10 October 2025, pp. 1-16
-
- Article
- Export citation
Harmonic exponential terms are polynomial
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2025, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hartshorne’s question on cofiniteness of complexes
- Part of:
-
- Published online by Cambridge University Press:
- 07 October 2025, pp. 1-14
-
- Article
- Export citation



















 .
.
























































