In this article, we investigate a free boundary problem for the Lotka–Volterra model consisting of an invasive species with density u and a native species with density v in one dimension. We assume that v undergoes diffusion and growth in 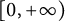$[0,+\infty )$, and u invades into the environment with spreading front $x=h(t)$ satisfying free boundary condition $h'(t)=-u_x(t,h(t))-\alpha $ for some decay rate 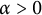$\alpha>0$, this is caused by the bad environment at the boundary. 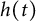When u is an inferior competitor, $u(t,x)$ and $h(t)$ tend to 0 within a finite time, while another specie 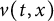$v(t,x)$ tends to a stationary 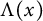$\Lambda (x)$ defined on the half-line. When u is a superior competitor, we have a trichotomy result: spreading of u and vanishing of v (i.e., as 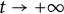$t \to +\infty $, $h(t)$ goes to $+\infty $ and 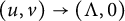$(u,v)\to (\Lambda ,0)$); the transition case (i.e., as 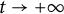$t \to +\infty $, $(u,v)\to (w_\alpha , \eta _\alpha )$, $h(t)$ tends to a finite point); vanishing of u and spreading of v (i.e., 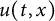$u(t,x)$ and $h(t)$ tends to 0 within a finite time, 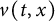$v(t,x)$ converges to 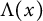$\Lambda (x)$). Additionally, we show that this trichotomy result depends on the initial data $u(0,x)$.