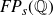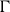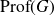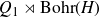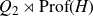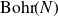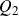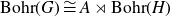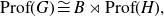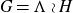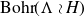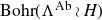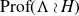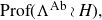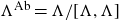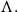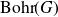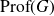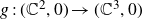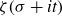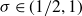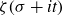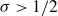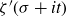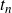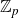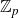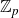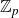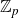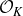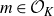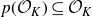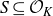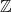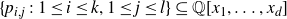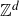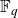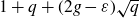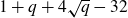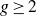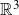Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
Three Schur functors related to pre-Lie algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 16 October 2023, pp. 441-458
- Print publication:
- March 2024
-
- Article
- Export citation

In Defence of a Dynamic View of Reality
-
- Published by:
- Jagiellonian University Press
- Published online:
- 14 October 2023
- Print publication:
- 29 April 2022
PSP volume 175 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 13 October 2023, pp. b1-b5
- Print publication:
- November 2023
-
- Article
-
- You have access
- Export citation
PSP volume 175 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 13 October 2023, pp. f1-f2
- Print publication:
- November 2023
-
- Article
-
- You have access
- Export citation
On subdirect products of type FPn of limit groups over Droms RAAGs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 417-440
- Print publication:
- March 2024
-
- Article
- Export citation
Abelian tropical covers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 October 2023, pp. 395-416
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Bohr compactifications and profinite completions of group extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 373-393
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonvarying, affine and extremal geometry of strata of differentials
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 361-371
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the topology of the transversal slice of a quasi-homogeneous map germ
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 339-359
- Print publication:
- March 2024
-
- Article
- Export citation
Spirals of Riemann’s Zeta-Function — Curvature, Denseness and Universality
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 325-338
- Print publication:
- March 2024
-
- Article
- Export citation
A problem of Erdős–Graham–Granville–Selfridge on integral points on hyperelliptic curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 309-323
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of fine Selmer groups over
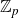 $\mathbb{Z}_{p}$-extensions
$\mathbb{Z}_{p}$-extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 287-308
- Print publication:
- March 2024
-
- Article
- Export citation
Multiple recurrence and popular differences for polynomial patterns in rings of integers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 239-278
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some torsion-free solvable groups with few subquotients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 279-286
- Print publication:
- March 2024
-
- Article
- Export citation
Lower bounds on the maximal number of rational points on curves over finite fields
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 213-238
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Categories of graphs for operadic structures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 155-212
- Print publication:
- January 2024
-
- Article
- Export citation
Non-Orientable Lagrangian Fillings of Legendrian Knots
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 123-153
- Print publication:
- January 2024
-
- Article
- Export citation
Chapter 4 - Solutions of the Schrödinger Equation in Three Dimensions
-
- Book:
- Quantum Mechanics with Concept Maps
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 95-126
-
- Chapter
- Export citation
Contents
-
- Book:
- Quantum Mechanics with Concept Maps
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp vii-x
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Quantum Mechanics with Concept Maps
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp iv-iv
-
- Chapter
- Export citation