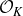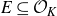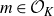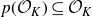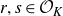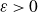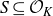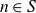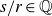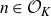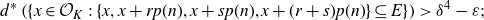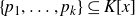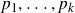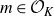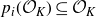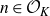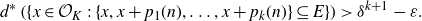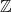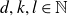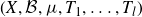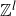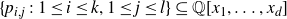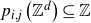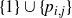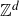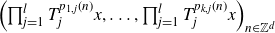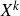1. Introduction
1·1. Background and main results
Let
![]() $(X, \mathcal{B}, \mu, T)$
be an invertible probability measure-preserving system. A classical result of Khintchine [
Reference Khintchine31
] says that for any
$(X, \mathcal{B}, \mu, T)$
be an invertible probability measure-preserving system. A classical result of Khintchine [
Reference Khintchine31
] says that for any
![]() $A \in \mathcal{B}$
,
$A \in \mathcal{B}$
,
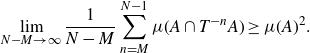 \begin{align*} \lim_{N - M \to \infty}{\frac{1}{N-M} \sum_{n=M}^{N-1}{\mu(A \cap T^{-n}A)}} \ge \mu(A)^2.\end{align*}
\begin{align*} \lim_{N - M \to \infty}{\frac{1}{N-M} \sum_{n=M}^{N-1}{\mu(A \cap T^{-n}A)}} \ge \mu(A)^2.\end{align*}
As a consequence, for any
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is syndetic, meaning that it has bounded gaps (equivalently, finitely many translates of R cover
![]() $\mathbb{Z}$
). Furstenberg showed in [
Reference Furstenberg22
] that for any
$\mathbb{Z}$
). Furstenberg showed in [
Reference Furstenberg22
] that for any
![]() $A \in \mathcal{B}$
and any
$A \in \mathcal{B}$
and any
![]() $k \in \mathbb{N}$
,
$k \in \mathbb{N}$
,
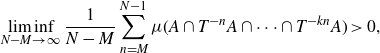 \begin{align*} \liminf_{N - M \to \infty}{\frac{1}{N-M} \sum_{n=M}^{N-1}{\mu(A \cap T^{-n}A \cap \dots \cap T^{-kn}A)}} > 0,\end{align*}
\begin{align*} \liminf_{N - M \to \infty}{\frac{1}{N-M} \sum_{n=M}^{N-1}{\mu(A \cap T^{-n}A \cap \dots \cap T^{-kn}A)}} > 0,\end{align*}
from which it follows that
is syndetic for some
![]() $c > 0$
. One may ask, for these longer expressions, if c can be made arbitrarily close to
$c > 0$
. One may ask, for these longer expressions, if c can be made arbitrarily close to
![]() $\mu(A)^{k+1}$
. (By considering weakly mixing systems, it is clear that c cannot exceed
$\mu(A)^{k+1}$
. (By considering weakly mixing systems, it is clear that c cannot exceed
![]() $\mu(A)^{k+1}$
in general.) A somewhat surprising answer was given in [
Reference Bergelson6
]:
$\mu(A)^{k+1}$
in general.) A somewhat surprising answer was given in [
Reference Bergelson6
]:
Theorem 1·1 ([ Reference Bergelson6 , theorems 1·2 and 1·3]).
-
(1) For any ergodic invertible probability measure-preserving system
 $(X, \mathcal{B}, \mu,T)$
, any
$(X, \mathcal{B}, \mu,T)$
, any
 $\varepsilon > 0$
, and any
$\varepsilon > 0$
, and any
 $A \in \mathcal{B}$
, the set (1·1)is syndetic.
$A \in \mathcal{B}$
, the set (1·1)is syndetic. \begin{align} \left\{ n \in \mathbb{Z} \;:\; \mu(A \cap T^{-n}A \cap T^{-2n}A) > \mu(A)^3 - \varepsilon \right\} \end{align}
\begin{align} \left\{ n \in \mathbb{Z} \;:\; \mu(A \cap T^{-n}A \cap T^{-2n}A) > \mu(A)^3 - \varepsilon \right\} \end{align}
-
(2) For any ergodic invertible probability measure-preserving system
 $(X, \mathcal{B}, \mu,T)$
, any
$(X, \mathcal{B}, \mu,T)$
, any
 $\varepsilon > 0$
, and any
$\varepsilon > 0$
, and any
 $A \in \mathcal{B}$
, the set is syndetic.
$A \in \mathcal{B}$
, the set is syndetic. \begin{align*} \left\{ n \in \mathbb{Z} \;:\; \mu(A \cap T^{-n} A \cap T^{-2n}A \cap T^{-3n}A) > \mu(A)^4 - \varepsilon \right\} \end{align*}
\begin{align*} \left\{ n \in \mathbb{Z} \;:\; \mu(A \cap T^{-n} A \cap T^{-2n}A \cap T^{-3n}A) > \mu(A)^4 - \varepsilon \right\} \end{align*}
-
(3) There exists an ergodic system
 $(X, \mathcal{B}, \mu, T)$
with the following property: for any integer
$(X, \mathcal{B}, \mu, T)$
with the following property: for any integer
 $l \geq 1$
, there is a set
$l \geq 1$
, there is a set
 $A =A(l) \in \mathcal{B}$
of positive measure such that for every integer
$A =A(l) \in \mathcal{B}$
of positive measure such that for every integer \begin{align*} \mu(A \cap T^{-n}A \cap T^{-2n} A \cap T^{-3n}A\cap T^{-4n}A ) \leq \frac 12\mu(A)^l \end{align*}
\begin{align*} \mu(A \cap T^{-n}A \cap T^{-2n} A \cap T^{-3n}A\cap T^{-4n}A ) \leq \frac 12\mu(A)^l \end{align*}
 $n \neq 0$
.
$n \neq 0$
.
In the terminology of [
Reference Ackelsberg, Bergelson and Best2
], Theorem 1·1 shows that the families
![]() $\{n, 2n\}$
and
$\{n, 2n\}$
and
![]() $\{n, 2n, 3n\}$
have the large intersections property, while
$\{n, 2n, 3n\}$
have the large intersections property, while
![]() $\{n, 2n, \dots, kn\}$
does not have the large intersections property for
$\{n, 2n, \dots, kn\}$
does not have the large intersections property for
![]() $k \ge 4$
. The combinatorial content, via Furstenberg’s correspondence principle, is that, for arithmetic progression of length 3 and 4, one can find a “popular” common difference: if
$k \ge 4$
. The combinatorial content, via Furstenberg’s correspondence principle, is that, for arithmetic progression of length 3 and 4, one can find a “popular” common difference: if
![]() $E \subseteq \mathbb{Z}$
has positive upper Banach density
$E \subseteq \mathbb{Z}$
has positive upper Banach density
![]() $d^*(E) = \delta > 0$
and
$d^*(E) = \delta > 0$
and
![]() $\varepsilon > 0$
, then there exists (syndetically many)
$\varepsilon > 0$
, then there exists (syndetically many)
![]() $n \ne 0$
such that
$n \ne 0$
such that
and there exists (syndetically many)
![]() $m \ne 0$
such that
$m \ne 0$
such that
A natural question to ask is whether various extensions of Szemerédi’s theorem also admit large intersections variants.
The polynomial Szemerédi theorem of the second author and Leibman [
Reference Bergelson and Leibman7
] extends Furstenberg’s result to polynomial configurations. We say that a polynomial
![]() $p(x) \in \mathbb{Q}[x]$
is integer-valued if
$p(x) \in \mathbb{Q}[x]$
is integer-valued if
![]() $p(\mathbb{Z}) \subseteq \mathbb{Z}$
.
$p(\mathbb{Z}) \subseteq \mathbb{Z}$
.
Theorem 1·2 ([
Reference Bergelson and Leibman7
, special case of theorem A]). Let
![]() $p_1, \dots, p_k \in \mathbb{Q}[x]$
be integer-valued polynomials with zero constant term. Then for any invertible probability measure-preserving system
$p_1, \dots, p_k \in \mathbb{Q}[x]$
be integer-valued polynomials with zero constant term. Then for any invertible probability measure-preserving system
![]() $(X, \mathcal{B}, \mu, T)$
and any
$(X, \mathcal{B}, \mu, T)$
and any
![]() $A \in \mathcal{B}$
with
$A \in \mathcal{B}$
with
![]() $\mu(A) > 0$
, there exists
$\mu(A) > 0$
, there exists
![]() $c > 0$
such that the set
$c > 0$
such that the set
has positive lower density, i.e.
![]() $\liminf_{N \to \infty}{{|R \cap \{1, \dots, N\}|}/{N}} > 0$
.
$\liminf_{N \to \infty}{{|R \cap \{1, \dots, N\}|}/{N}} > 0$
.
The conclusion of Theorem 1·2 was strengthened in [
Reference Bergelson and McCutcheon12
, theorem 0·1], where it was shown that R is syndetic for some
![]() $c > 0$
depending on A.
$c > 0$
depending on A.
There is a wider variety of combinatorial configurations in play when polynomials are introduced, and there is not yet a full classification of which families of polynomials have the large intersections property. However, large intersections variants of the polynomial Szemerédi theorem are known for two natural classes of polynomial configurations: independent polynomials and polynomials that are integer multiples of a fixed polynomial (for
![]() $k=2, 3$
). This is summarised by the following two results, which we seek to extend in this paper:
$k=2, 3$
). This is summarised by the following two results, which we seek to extend in this paper:
Theorem 1·3 ([
Reference Frantzikinakis and Kra21
, theorem 1·3]). Let
![]() $p_1, \dots, p_k \in \mathbb{Q}[x]$
be linearly independent integer-valued polynomials with zero constant term. Then for any invertible probability measure-preserving system, any
$p_1, \dots, p_k \in \mathbb{Q}[x]$
be linearly independent integer-valued polynomials with zero constant term. Then for any invertible probability measure-preserving system, any
![]() $A \in \mathcal{B}$
, and any
$A \in \mathcal{B}$
, and any
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is syndetic.
Theorem 1·4 ([
Reference Frantzikinakis19
, theorem C]). Let
![]() $p \in \mathbb{Q}[x]$
be an integer-valued polynomial with zero constant term, and let
$p \in \mathbb{Q}[x]$
be an integer-valued polynomial with zero constant term, and let
![]() $a, b \in \mathbb{Z}$
be nonzero and distinct. Then for any ergodic invertible probability measure-preserving system, any
$a, b \in \mathbb{Z}$
be nonzero and distinct. Then for any ergodic invertible probability measure-preserving system, any
![]() $A \in \mathcal{B}$
, and any
$A \in \mathcal{B}$
, and any
![]() $\varepsilon > 0$
, the sets
$\varepsilon > 0$
, the sets
and
are syndetic.
We have so far stated all results about polynomial multiple recurrence only for polynomials with zero constant term. The essential feature of such families of polynomials is that they avoid “local obstructions.” To be precise, we say that a family of polynomials
![]() $\{p_1, \dots, p_k\}$
is jointly intersective if for every
$\{p_1, \dots, p_k\}$
is jointly intersective if for every
![]() $m \in \mathbb{N}$
, there exists
$m \in \mathbb{N}$
, there exists
![]() $n \in \mathbb{Z}$
such that
$n \in \mathbb{Z}$
such that
![]() $p_i(n) \in m\mathbb{Z}$
for every
$p_i(n) \in m\mathbb{Z}$
for every
![]() $i = 1, \dots, k$
. If a family of polynomials is not jointly intersective, then the set appearing in (1·2) will be trivial for some rotations on finitely many points. In [
Reference Bergelson, Leibman and Lesigne11
], it was shown that there are no other obstacles to multiple recurrence:
$i = 1, \dots, k$
. If a family of polynomials is not jointly intersective, then the set appearing in (1·2) will be trivial for some rotations on finitely many points. In [
Reference Bergelson, Leibman and Lesigne11
], it was shown that there are no other obstacles to multiple recurrence:
Theorem 1·5 ([
Reference Bergelson, Leibman and Lesigne11
, theorem 1·1]). For a family of integer-valued polynomials
![]() $\mathcal{P} = \{p_1, \dots, p_k\} \subseteq \mathbb{Q}[x]$
, the following are equivalent:
$\mathcal{P} = \{p_1, \dots, p_k\} \subseteq \mathbb{Q}[x]$
, the following are equivalent:
-
(i)
 $\mathcal{P}$
is jointly intersective;
$\mathcal{P}$
is jointly intersective;
-
(ii) for any probability measure-preserving system
 $(X, \mathcal{B}, \mu, T)$
and any
$(X, \mathcal{B}, \mu, T)$
and any
 $A \in \mathcal{B}$
, there exists
$A \in \mathcal{B}$
, there exists
 $c > 0$
such that is syndetic.
$c > 0$
such that is syndetic. \begin{align*} \left\{ n \in \mathbb{Z} \;:\; \mu \left( A \cap T^{-p_1(n)}A \cap \dots \cap T^{-p_k(n)}A \right) > c \right\} \end{align*}
\begin{align*} \left\{ n \in \mathbb{Z} \;:\; \mu \left( A \cap T^{-p_1(n)}A \cap \dots \cap T^{-p_k(n)}A \right) > c \right\} \end{align*}
The proofs of Theorems 1·3 and 1·4 can also be easily modified to apply to families of jointly intersective polynomials.
The polynomial Szemerédi theorem is in fact known for polynomials of several variables with zero constant term (see [
Reference Bergelson and Leibman7
, theorem A] for the result with positive lower density and [
Reference Bergelson and McCutcheon13
, theorem 0·7] for syndeticity). For polynomials arising from rings of integers, the polynomial Szemerédi theorem holds for all jointly intersective polynomials. We now make this result precise. Fix a number field K and denote by
![]() $\mathcal{O}_K$
its ring of integers. By an
$\mathcal{O}_K$
its ring of integers. By an
![]() $\mathcal{O}_K$
-system, we will mean a quadruple
$\mathcal{O}_K$
-system, we will mean a quadruple
![]() $(X, \mathcal{B}, \mu, T)$
, where T is a measure-preserving action of
$(X, \mathcal{B}, \mu, T)$
, where T is a measure-preserving action of
![]() $(\mathcal{O}_K,+)$
on a probability space
$(\mathcal{O}_K,+)$
on a probability space
![]() $(X, \mathcal{B}, \mu)$
.
$(X, \mathcal{B}, \mu)$
.
Definition 1·6. A family of
![]() $\mathcal{O}_K$
-valued polynomials
$\mathcal{O}_K$
-valued polynomials
![]() $\{p_1, \dots, p_k\}$
is jointly intersective if for every finite index subgroup
$\{p_1, \dots, p_k\}$
is jointly intersective if for every finite index subgroup
![]() $\Lambda \subseteq (\mathcal{O}_K, +)$
, there exists
$\Lambda \subseteq (\mathcal{O}_K, +)$
, there exists
![]() $\xi \in \mathcal{O}_K$
such that
$\xi \in \mathcal{O}_K$
such that
![]() $\{p_1(\xi), \dots, p_k(\xi)\} \subseteq \Lambda$
.
$\{p_1(\xi), \dots, p_k(\xi)\} \subseteq \Lambda$
.
Recall that in an abelian group G, a set
![]() $E \subseteq G$
is syndetic if finitely many translates of E cover G. That is,
$E \subseteq G$
is syndetic if finitely many translates of E cover G. That is,
![]() $G = \bigcup_{i=1}^m{(E + g_i)}$
for some
$G = \bigcup_{i=1}^m{(E + g_i)}$
for some
![]() $g_1, \dots, g_m \in G$
.
$g_1, \dots, g_m \in G$
.
Theorem 1·7 ([
Reference Bergelson and Robertson14
, theorem 1·6]). Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $p_1, \dots, p_k \in \mathcal{O}_K[x]$
be jointly intersective polynomials. For any
$p_1, \dots, p_k \in \mathcal{O}_K[x]$
be jointly intersective polynomials. For any
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $(X, \mathcal{B}, \mu, T)$
and any
$(X, \mathcal{B}, \mu, T)$
and any
![]() $A \in \mathcal{B}$
, there exists
$A \in \mathcal{B}$
, there exists
![]() $c > 0$
such that the set
$c > 0$
such that the set
is syndetic.
It is therefore natural to ask whether Khintchine-type recurrence theorems hold for polynomial configurations in rings of integers. That is, under what conditions on the polynomials
![]() $\{p_1, \dots, p_k\}$
can the constant c in (1·3) be made arbitrarily close to
$\{p_1, \dots, p_k\}$
can the constant c in (1·3) be made arbitrarily close to
![]() $\mu(A)^{k+1}$
?
$\mu(A)^{k+1}$
?
In this paper, we provide an answer to this question in natural and important cases by proving extensions of Theorems 1·3 and 1·4.
Theorem A.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
$\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
![]() $\mathcal{O}_K$
-valued polynomials. Then for any measure-preserving
$\mathcal{O}_K$
-valued polynomials. Then for any measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
,
$\left( X, \mathcal{B}, \mu, T \right)$
,
![]() $A \in \mathcal{B}$
, and
$A \in \mathcal{B}$
, and
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is syndetic.
Theorem B.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $p(x) \in K[x]$
be an
$p(x) \in K[x]$
be an
![]() $\mathcal{O}_K$
-valued intersective polynomial. Let
$\mathcal{O}_K$
-valued intersective polynomial. Let
![]() $r,s \in \mathcal{O}_K$
be distinct and nonzero. Then for any ergodic measure-preserving
$r,s \in \mathcal{O}_K$
be distinct and nonzero. Then for any ergodic measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
,
$\left( X, \mathcal{B}, \mu, T \right)$
,
![]() $A \in \mathcal{B}$
, and
$A \in \mathcal{B}$
, and
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is syndetic.
Moreover, if
![]() ${s}/{r} \in \mathbb{Q}$
, then
${s}/{r} \in \mathbb{Q}$
, then
is syndetic.
Note that for a pair of polynomials
![]() $\{p,q\} \subseteq K[x] \setminus \{0\}$
, either p and q are linearly independent over K or
$\{p,q\} \subseteq K[x] \setminus \{0\}$
, either p and q are linearly independent over K or
![]() $q = cp$
for some
$q = cp$
for some
![]() $c \in K$
. Thus, we have the following immediate consequence of Theorems A and B together:
$c \in K$
. Thus, we have the following immediate consequence of Theorems A and B together:
Corollary 1·8.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Suppose
$\mathcal{O}_K$
. Suppose
![]() $\{p, q\} \subseteq K[x]$
is a jointly intersective pair of
$\{p, q\} \subseteq K[x]$
is a jointly intersective pair of
![]() $\mathcal{O}_K$
-valued polynomials. Then for any ergodic measure-preserving
$\mathcal{O}_K$
-valued polynomials. Then for any ergodic measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
, any
$\left( X, \mathcal{B}, \mu, T \right)$
, any
![]() $A \in \mathcal{B}$
, and any
$A \in \mathcal{B}$
, and any
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is syndetic.
Theorem A shows that for independent families of any size, we can achieve Khintchine-type results. In contrast, Theorem B only demonstrates a Khintchine-type result for configurations of length three or four and requires ergodicity of the system (for counterexamples in the non-ergodic case, see [
Reference Ackelsberg, Bergelson and Best2
, section 11·1]). Moreover, for length four, we have made additional assumptions, which we discuss below. To complete the picture, we now address what happens for patterns of length five and longer. For concreteness, let us consider general polynomial families of the form
![]() $\{a_1p, \dots, a_kp\}$
, where
$\{a_1p, \dots, a_kp\}$
, where
![]() $a_i \in \mathcal{O}_K$
and
$a_i \in \mathcal{O}_K$
and
![]() $p(x) \in K[x]$
is
$p(x) \in K[x]$
is
![]() $\mathcal{O}_K$
-valued. In the simplest case when
$\mathcal{O}_K$
-valued. In the simplest case when
![]() $K = \mathbb{Q}$
and
$K = \mathbb{Q}$
and
![]() $a_i = i$
, a combinatorial construction of Ruzsa rules out Khintchine-type results when
$a_i = i$
, a combinatorial construction of Ruzsa rules out Khintchine-type results when
![]() $k \ge 4$
(see item 3 of Theorem 1·1 above). In [
Reference Ackelsberg, Bergelson and Best2
, corollary 12·14], this was generalised to any number field K and any integers
$k \ge 4$
(see item 3 of Theorem 1·1 above). In [
Reference Ackelsberg, Bergelson and Best2
, corollary 12·14], this was generalised to any number field K and any integers
![]() $a_i \in \mathbb{Z}$
for
$a_i \in \mathbb{Z}$
for
![]() $k \ge 4$
. Furthermore, [
Reference Ackelsberg, Bergelson and Best2
, proposition 12·13] gives a combinatorial criterion for checking the case
$k \ge 4$
. Furthermore, [
Reference Ackelsberg, Bergelson and Best2
, proposition 12·13] gives a combinatorial criterion for checking the case
![]() $k = 4$
for any coefficients
$k = 4$
for any coefficients
![]() $a_i \in \mathcal{O}_K$
. We do not know how to prove the requisite combinatorial result, but we believe that Khintchine-type results will fail for any non-trivial family
$a_i \in \mathcal{O}_K$
. We do not know how to prove the requisite combinatorial result, but we believe that Khintchine-type results will fail for any non-trivial family
![]() $\{a_1p, \dots, a_kp\}$
with
$\{a_1p, \dots, a_kp\}$
with
![]() $k \ge 4$
.
$k \ge 4$
.
Now we turn to the other conditions imposed for the patterns of length four appearing in Theorem B. The strategy of proof in Theorem B is to reduce to the linear case
![]() $p(n) = n$
and then apply knowledge about linear patterns. General Khintchine-type results for linear patterns appear in [
Reference Ackelsberg, Bergelson and Best2
] (subsequently improved in [
Reference Ackelsberg1, Reference Ackelsberg, Bergelson and Shalom3
]), where a similar distinction is made between patterns of length three and of length four:
$p(n) = n$
and then apply knowledge about linear patterns. General Khintchine-type results for linear patterns appear in [
Reference Ackelsberg, Bergelson and Best2
] (subsequently improved in [
Reference Ackelsberg1, Reference Ackelsberg, Bergelson and Shalom3
]), where a similar distinction is made between patterns of length three and of length four:
Theorem 1·9 ([
Reference Ackelsberg, Bergelson and Best2
, theorems 1·10 and 1·11]). Let
![]() $(G,+)$
be a countable discrete abelian group. Let
$(G,+)$
be a countable discrete abelian group. Let
![]() $\left( X, \mathcal{B}, \mu, (T_g)_{g \in G} \right)$
be an ergodic measure-preserving G-system. Let
$\left( X, \mathcal{B}, \mu, (T_g)_{g \in G} \right)$
be an ergodic measure-preserving G-system. Let
![]() $A \in \mathcal{B}$
and
$A \in \mathcal{B}$
and
![]() $\varepsilon > 0$
.
$\varepsilon > 0$
.
-
(1) suppose
 $\varphi, \psi \;:\; G \to G$
are homomorphisms such that the subgroups
$\varphi, \psi \;:\; G \to G$
are homomorphisms such that the subgroups
 $\varphi(G)$
,
$\varphi(G)$
,
 $\psi(G)$
, and
$\psi(G)$
, and
 $(\psi-\varphi)(G)$
have finite index in G. Then is syndetic in G.
$(\psi-\varphi)(G)$
have finite index in G. Then is syndetic in G. \begin{align*} \left\{ g \in G \;:\; \mu \left( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A \right) > \mu(A)^3 - \varepsilon \right\} \end{align*}
\begin{align*} \left\{ g \in G \;:\; \mu \left( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A \right) > \mu(A)^3 - \varepsilon \right\} \end{align*}
-
(2) suppose
 $r, s \in \mathbb{Z}$
are distinct and nonzero such that the subgroups rG, sG,
$r, s \in \mathbb{Z}$
are distinct and nonzero such that the subgroups rG, sG,
 $(r+s)G$
, and
$(r+s)G$
, and
 $(s-r)G$
have finite index in G. Then is syndetic in G.
$(s-r)G$
have finite index in G. Then is syndetic in G. \begin{align*} \left\{ g \in G \;:\; \mu \left( A \cap T_{rg}^{-1}A \cap T_{sg}^{-1}A \cap T_{(r+s)g}^{-1}A \right) > \mu(A)^4 - \varepsilon \right\} \end{align*}
\begin{align*} \left\{ g \in G \;:\; \mu \left( A \cap T_{rg}^{-1}A \cap T_{sg}^{-1}A \cap T_{(r+s)g}^{-1}A \right) > \mu(A)^4 - \varepsilon \right\} \end{align*}
The second half of Theorem 1·9 was also proved independently in [
Reference Shalom37
, theorem 1·3]. By absorbing a constant into the polynomial p in Theorem B, imposing the condition
![]() $\frac{s}{r} \in \mathbb{Q}$
is equivalent to assuming
$\frac{s}{r} \in \mathbb{Q}$
is equivalent to assuming
![]() $r, s \in \mathbb{Z}$
, so our assumptions allow us to apply Theorem 1·9 in the linear case
$r, s \in \mathbb{Z}$
, so our assumptions allow us to apply Theorem 1·9 in the linear case
![]() $p(n) = n$
.
$p(n) = n$
.
In [
Reference Berger, Sah, Sawhney and Tidor16
], it was shown that, for a related finitary problem, there are automorphisms
![]() $\varphi$
and
$\varphi$
and
![]() $\psi$
such that
$\psi$
such that
![]() $\varphi + \psi$
and
$\varphi + \psi$
and
![]() $\psi - \varphi$
are also automorphisms but for which a Khintchine-type result fails:
$\psi - \varphi$
are also automorphisms but for which a Khintchine-type result fails:
Theorem 1·10 ([
Reference Berger, Sah, Sawhney and Tidor16
, theorem 1·3]). There is an absolute constant
![]() $c > 0$
such that the following holds. If
$c > 0$
such that the following holds. If
![]() $\alpha \in (0, c)$
, then for all sufficiently large n (depending on
$\alpha \in (0, c)$
, then for all sufficiently large n (depending on
![]() $\alpha$
), there is a set
$\alpha$
), there is a set
![]() $A \subseteq (\mathbb{F}_5^n)^2$
with
$A \subseteq (\mathbb{F}_5^n)^2$
with
![]() $|A| \ge \alpha \cdot 5^{2n}$
such that
$|A| \ge \alpha \cdot 5^{2n}$
such that
for all
![]() $(a, b) \in (\mathbb{F}_5^n)^2 \setminus \{(0,0)\}$
.
$(a, b) \in (\mathbb{F}_5^n)^2 \setminus \{(0,0)\}$
.
The authors of [ Reference Berger, Sah, Sawhney and Tidor16 ] explain the failure of large intersections in Theorem 1·10 as a consequence of an eigenvalue condition. Namely, for the corresponding matrices
the eigenvalues of
![]() $M_1M_2^{-1}$
are negatives of each other. They also show that in the absence of such an eigenvalue condition, a Khintchine-type result holds for patterns
$M_1M_2^{-1}$
are negatives of each other. They also show that in the absence of such an eigenvalue condition, a Khintchine-type result holds for patterns
(see [ Reference Berger, Sah, Sawhney and Tidor16 , theorem 1·2]).
In our context of rings of integers, we can translate the eigenvalue condition into an algebraic criterion. Recall that two algebraic numbers
![]() $\alpha, \beta \in K$
are conjugate (over
$\alpha, \beta \in K$
are conjugate (over
![]() $\mathbb{Q}$
) if they have the same minimal polynomial (over
$\mathbb{Q}$
) if they have the same minimal polynomial (over
![]() $\mathbb{Q}$
). Equivalently, there is a field automorphism
$\mathbb{Q}$
). Equivalently, there is a field automorphism
![]() $\varphi \;:\; K \to K$
such that
$\varphi \;:\; K \to K$
such that
![]() $\varphi(\alpha) = \beta$
. If we denote by
$\varphi(\alpha) = \beta$
. If we denote by
![]() $M_{\alpha}$
the
$M_{\alpha}$
the
![]() $\mathbb{Q}$
-linear map
$\mathbb{Q}$
-linear map
![]() $M_{\alpha}x = \alpha x$
on the
$M_{\alpha}x = \alpha x$
on the
![]() $\mathbb{Q}$
-vector space K, then the eigenvalues of
$\mathbb{Q}$
-vector space K, then the eigenvalues of
![]() $M_{\alpha}$
are exactly the conjugates of
$M_{\alpha}$
are exactly the conjugates of
![]() $\alpha$
(this follows from, e.g., [
Reference Conrad18
, theorem 5·9], which gives a formula for the characteristic polynomial of
$\alpha$
(this follows from, e.g., [
Reference Conrad18
, theorem 5·9], which gives a formula for the characteristic polynomial of
![]() $M_{\alpha}$
). We therefore make the following conjecture:
$M_{\alpha}$
). We therefore make the following conjecture:
Conjecture 1·11.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $r, s \in \mathcal{O}_K$
be distinct and nonzero. The following are equivalent:
$r, s \in \mathcal{O}_K$
be distinct and nonzero. The following are equivalent:
-
(i) for any ergodic measure-preserving
 $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
 $(X, \mathcal{B}, \mu, T)$
, any
$(X, \mathcal{B}, \mu, T)$
, any
 $A \in \mathcal{B}$
, any
$A \in \mathcal{B}$
, any
 $\varepsilon > 0$
, and any
$\varepsilon > 0$
, and any
 $\mathcal{O}_K$
-valued intersective polynomial
$\mathcal{O}_K$
-valued intersective polynomial
 $p \in K[x]$
, the set is syndetic;
$p \in K[x]$
, the set is syndetic; \begin{align*} \left\{ n \in \mathcal{O}_K \;:\; \mu \left( A \cap T^{-rp(n)}A \cap T^{-sp(n)}A \cap T^{-(r+s)p(n)}A \right) > \mu(A)^4 - \varepsilon \right\} \end{align*}
\begin{align*} \left\{ n \in \mathcal{O}_K \;:\; \mu \left( A \cap T^{-rp(n)}A \cap T^{-sp(n)}A \cap T^{-(r+s)p(n)}A \right) > \mu(A)^4 - \varepsilon \right\} \end{align*}
-
(ii) no two conjugates of
 ${s}/{r}$
over
${s}/{r}$
over
 $\mathbb{Q}$
are negatives of each other.
$\mathbb{Q}$
are negatives of each other.
1·2. Method
In order to prove Khintchine-type recurrence results such as Theorem A and Theorem B, it is natural to consider associated multiple ergodic averages. The appropriate averaging schemes in rings of integers are those arising from Følner sequences. A Følner sequence in
![]() $(\mathcal{O}_K, +)$
is a sequence of subsets
$(\mathcal{O}_K, +)$
is a sequence of subsets
![]() $(\Phi_N)_{N \in \mathbb{N}}$
of
$(\Phi_N)_{N \in \mathbb{N}}$
of
![]() $\mathcal{O}_K$
such that, for every
$\mathcal{O}_K$
such that, for every
![]() $n \in \mathcal{O}_K$
,
$n \in \mathcal{O}_K$
,
Examples of Følner sequences include boxes in
![]() $\mathcal{O}_K \cong \mathbb{Z}^d$
with increasing side lengths. We say that a sequence
$\mathcal{O}_K \cong \mathbb{Z}^d$
with increasing side lengths. We say that a sequence
![]() $(u_n)_{n \in \mathcal{O}_K}$
has uniform Cesàro limit u, denoted
$(u_n)_{n \in \mathcal{O}_K}$
has uniform Cesàro limit u, denoted
![]() $\text{UC-}\lim_{n \in \mathcal{O}_K}{u_n} = u$
, if
$\text{UC-}\lim_{n \in \mathcal{O}_K}{u_n} = u$
, if
for every Følner sequence
![]() $(\Phi_N)_{N \in \mathbb{N}}$
in
$(\Phi_N)_{N \in \mathbb{N}}$
in
![]() $(\mathcal{O}_K, +)$
. The usefulness of uniform Cesàro limits in proving Khintchine-type theorems comes from the following routine fact (for a proof, see [
Reference Ackelsberg, Bergelson and Best2
, lemma 1·9]):
$(\mathcal{O}_K, +)$
. The usefulness of uniform Cesàro limits in proving Khintchine-type theorems comes from the following routine fact (for a proof, see [
Reference Ackelsberg, Bergelson and Best2
, lemma 1·9]):
Proposition 1·12.
A set
![]() $S \subseteq \mathcal{O}_K$
is syndetic if and only if for any Følner sequence
$S \subseteq \mathcal{O}_K$
is syndetic if and only if for any Følner sequence
![]() $(\Phi_N)_{N \in \mathbb{N}}$
in
$(\Phi_N)_{N \in \mathbb{N}}$
in
![]() $(\mathcal{O}_K, +)$
, one has
$(\mathcal{O}_K, +)$
, one has
![]() $\bigcup_{N \in \mathbb{N}}{\Phi_N} \cap S \ne \emptyset$
.
$\bigcup_{N \in \mathbb{N}}{\Phi_N} \cap S \ne \emptyset$
.
Rather than computing the multiple ergodic averages
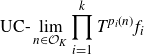 \begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}}\end{align}
\begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}}\end{align}
directly for an arbitrary
![]() $\mathcal{O}_K$
-system, we reduce to computing the averages (1·7) in simpler classes of systems. To be precise, we say a system
$\mathcal{O}_K$
-system, we reduce to computing the averages (1·7) in simpler classes of systems. To be precise, we say a system
![]() $\textbf{Y} = \left( Y, \mathcal{D}, \nu, S \right)$
is a factor of
$\textbf{Y} = \left( Y, \mathcal{D}, \nu, S \right)$
is a factor of
![]() $\textbf{X} = \left( X, \mathcal{B}, \mu, T \right)$
if there are full measure subsets
$\textbf{X} = \left( X, \mathcal{B}, \mu, T \right)$
if there are full measure subsets
![]() $X_0 \subseteq X$
and
$X_0 \subseteq X$
and
![]() $Y_0 \subseteq Y$
and a measure-preserving map
$Y_0 \subseteq Y$
and a measure-preserving map
![]() $\pi \;:\; X_0 \to Y_0$
such that
$\pi \;:\; X_0 \to Y_0$
such that
![]() $S^n\pi(x) = \pi(T^nx)$
for every
$S^n\pi(x) = \pi(T^nx)$
for every
![]() $x \in X_0$
,
$x \in X_0$
,
![]() $n \in \mathcal{O}_K$
. There is a natural correspondence between the factor Y and the T-invariant sub-
$n \in \mathcal{O}_K$
. There is a natural correspondence between the factor Y and the T-invariant sub-
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\pi^{-1}(\mathcal{D})$
. This allows us to take conditional expectations, and in a standard abuse of notation, we write
$\pi^{-1}(\mathcal{D})$
. This allows us to take conditional expectations, and in a standard abuse of notation, we write
![]() $\mathbb{E}\left[ {f} \mid {Y} \right] \;:\!=\; \mathbb{E}\left[ {f} \mid {\pi^{-1}(\mathcal{D})} \right]$
. The factor
$\mathbb{E}\left[ {f} \mid {Y} \right] \;:\!=\; \mathbb{E}\left[ {f} \mid {\pi^{-1}(\mathcal{D})} \right]$
. The factor
![]() $\textbf{Y}$
is characteristic for a family of sequences
$\textbf{Y}$
is characteristic for a family of sequences
![]() $\{a_1(n), \dots, a_k(n)\}, n \in \mathcal{O}_K$
, if for any
$\{a_1(n), \dots, a_k(n)\}, n \in \mathcal{O}_K$
, if for any
![]() $f_1, \dots, f_k \in L^{\infty}(\mu)$
,
$f_1, \dots, f_k \in L^{\infty}(\mu)$
,
 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\left( \prod_{i=1}^k{T^{a_i(n)}f_i} - \prod_{i=1}^k{T^{a_i(n)}\mathbb{E}\left[ {f_i} \mid {Y} \right]} \right)} = 0\end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\left( \prod_{i=1}^k{T^{a_i(n)}f_i} - \prod_{i=1}^k{T^{a_i(n)}\mathbb{E}\left[ {f_i} \mid {Y} \right]} \right)} = 0\end{align*}
in
![]() $L^2(\mu)$
.
$L^2(\mu)$
.
The main family of factors that we will deal with is the family of nilfactors
![]() $(\mathcal{Z}_r)_{r \in \mathbb{N}}$
(also called Host–Kra factors from the work of Host and Kra on
$(\mathcal{Z}_r)_{r \in \mathbb{N}}$
(also called Host–Kra factors from the work of Host and Kra on
![]() $\mathbb{Z}$
-actions [
Reference Host and Kra30
]). Assume for this discussion that T is an ergodic action of
$\mathbb{Z}$
-actions [
Reference Host and Kra30
]). Assume for this discussion that T is an ergodic action of
![]() $\mathcal{O}_K$
. The factor
$\mathcal{O}_K$
. The factor
![]() $\mathcal{Z}_r$
is defined to be the minimal factor that is characteristic for all families
$\mathcal{Z}_r$
is defined to be the minimal factor that is characteristic for all families
![]() $\{l_1n, \dots, l_{r+1}n\}$
with
$\{l_1n, \dots, l_{r+1}n\}$
with
![]() $l_1, \dots, l_{r+1} \in \mathcal{O}_K$
distinct and nonzero. For our purposes, it will suffice to discuss some general properties of nilfactors.
$l_1, \dots, l_{r+1} \in \mathcal{O}_K$
distinct and nonzero. For our purposes, it will suffice to discuss some general properties of nilfactors.
The tower of factors
![]() $\mathcal{Z}_1 \subseteq \mathcal{Z}_2 \subseteq \dots$
is a sequence of compact extensions. The first factor,
$\mathcal{Z}_1 \subseteq \mathcal{Z}_2 \subseteq \dots$
is a sequence of compact extensions. The first factor,
![]() $\mathcal{Z}_1$
, is the Kronecker factor, which is the smallest factor for which every eigenfunction is measurable. As a measure-preserving system, it is isomorphic to an action by rotations on a compact abelian group. The Kronecker factor contains a subfactor that will also be of interest, namely the rational Kronecker factor, denoted
$\mathcal{Z}_1$
, is the Kronecker factor, which is the smallest factor for which every eigenfunction is measurable. As a measure-preserving system, it is isomorphic to an action by rotations on a compact abelian group. The Kronecker factor contains a subfactor that will also be of interest, namely the rational Kronecker factor, denoted
![]() $\mathcal{K}_{rat}$
, which is an inverse limit of finite rotational systems (for a more detailed discussion of the rational Kronecker factor, see Section 2.1).
$\mathcal{K}_{rat}$
, which is an inverse limit of finite rotational systems (for a more detailed discussion of the rational Kronecker factor, see Section 2.1).
The higher-level nilfactors also have the structure of (inverse limits of) “rotational” systems but on more complex algebraic objects. Let G be an r-step nilpotent Lie group and
![]() $\Gamma < G$
a co-compact discrete subgroup. The quotient space
$\Gamma < G$
a co-compact discrete subgroup. The quotient space
![]() $X = G/\Gamma$
is called an r-step nilmanifold. An r-step nilsystem is a system
$X = G/\Gamma$
is called an r-step nilmanifold. An r-step nilsystem is a system
![]() $(X, \mathcal{B}, \mu, T)$
, where
$(X, \mathcal{B}, \mu, T)$
, where
![]() $X = G/\Gamma$
is an r-step nilmanifold,
$X = G/\Gamma$
is an r-step nilmanifold,
![]() $\mu$
is the Haar probability measure on X, and T is an
$\mu$
is the Haar probability measure on X, and T is an
![]() $(\mathcal{O}_K,+)$
-action by niltranslations, i.e. transformations of the form
$(\mathcal{O}_K,+)$
-action by niltranslations, i.e. transformations of the form
![]() $x \mapsto ax$
for some
$x \mapsto ax$
for some
![]() $a \in G$
. The nilfactor
$a \in G$
. The nilfactor
![]() $\mathcal{Z}_r$
is an inverse limit of r-step nilsystems. For
$\mathcal{Z}_r$
is an inverse limit of r-step nilsystems. For
![]() $\mathbb{Z}$
-actions, this was established by Host and Kra in [
Reference Host and Kra30
] and independently by Ziegler in [
Reference Ziegler39
]. For our generality of
$\mathbb{Z}$
-actions, this was established by Host and Kra in [
Reference Host and Kra30
] and independently by Ziegler in [
Reference Ziegler39
]. For our generality of
![]() $\mathcal{O}_K$
-systems, this follows from [
Reference Griesmer27
, theorem 4·1·2].
$\mathcal{O}_K$
-systems, this follows from [
Reference Griesmer27
, theorem 4·1·2].
By careful application of the van der Corput differencing trick, one can reduce polynomial expressions to (potentially much longer) linear expressions. This works so long as the polynomials
![]() $p_1, \dots, p_k$
are essentially distinct, meaning that
$p_1, \dots, p_k$
are essentially distinct, meaning that
![]() $p_j - p_i$
is non-constant for every
$p_j - p_i$
is non-constant for every
![]() $i \ne j$
. Hence, for any family of essentially distinct polynomial sequences
$i \ne j$
. Hence, for any family of essentially distinct polynomial sequences
![]() $\{p_1(n), \dots, p_k(n)\}, n \in \mathcal{O}_K$
, there is a characteristic factor that is a nilfactor (but the step of the nilfactor may far exceed
$\{p_1(n), \dots, p_k(n)\}, n \in \mathcal{O}_K$
, there is a characteristic factor that is a nilfactor (but the step of the nilfactor may far exceed
![]() $k-1$
in general):
$k-1$
in general):
Theorem 1·13 (cf. [
Reference Bergelson and Robertson14
, theorem 5·2]). Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Suppose
$\mathcal{O}_K$
. Suppose
![]() $\{p_1, \dots, p_k\} \subseteq K[x]$
are non-constant and essentially distinct
$\{p_1, \dots, p_k\} \subseteq K[x]$
are non-constant and essentially distinct
![]() $\mathcal{O}_K$
-valued polynomials. Then there is an
$\mathcal{O}_K$
-valued polynomials. Then there is an
![]() $r \in \mathbb{N}$
such that for any ergodic
$r \in \mathbb{N}$
such that for any ergodic
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $(X, \mathcal{B}, \mu, T)$
and any
$(X, \mathcal{B}, \mu, T)$
and any
![]() $f_1, \dots, f_k \in L^{\infty}(\mu)$
,
$f_1, \dots, f_k \in L^{\infty}(\mu)$
,
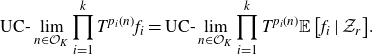 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)} \mathbb{E}\left[ {f_i} \mid {\mathcal{Z}_r} \right]}}. \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)} \mathbb{E}\left[ {f_i} \mid {\mathcal{Z}_r} \right]}}. \end{align*}
in
![]() $L^2(\mu)$
.
$L^2(\mu)$
.
For the specific configurations appearing in Theorem A (independent polynomials) and in Theorem B (multiples of a single polynomial), we can control the step of the characteristic nilfactors. In order to properly formulate our results, we need one more definition.
Definition 1·14. A family of polynomials
![]() $\{p_1, \dots, p_k\} \subseteq K[x]$
is independent if for all
$\{p_1, \dots, p_k\} \subseteq K[x]$
is independent if for all
![]() $(c_1, \dots, c_k) \in K^k \setminus \{0\}$
, the polynomial
$(c_1, \dots, c_k) \in K^k \setminus \{0\}$
, the polynomial
![]() $\sum_{i=1}^k{c_ip_i}$
is non-constant.
$\sum_{i=1}^k{c_ip_i}$
is non-constant.
Note that the family
![]() $\{p_1, \dots, p_k\}$
is independent if and only if
$\{p_1, \dots, p_k\}$
is independent if and only if
![]() $\{1, p_1, \dots, p_k\}$
is linearly independent over K. Furthermore, a jointly intersective family
$\{1, p_1, \dots, p_k\}$
is linearly independent over K. Furthermore, a jointly intersective family
![]() $\{p_1, \dots, p_k\}$
is independent if and only if it is linearly independent.
$\{p_1, \dots, p_k\}$
is independent if and only if it is linearly independent.
Theorem C.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Suppose
$\mathcal{O}_K$
. Suppose
![]() $p_1, \dots, p_k \in K[x]$
are independent and
$p_1, \dots, p_k \in K[x]$
are independent and
![]() $\mathcal{O}_K$
-valued. Then for any ergodic measure-preserving
$\mathcal{O}_K$
-valued. Then for any ergodic measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
and any
$\left( X, \mathcal{B}, \mu, T \right)$
and any
![]() $f_1, \dots, f_k \in L^{\infty}(\mu)$
,
$f_1, \dots, f_k \in L^{\infty}(\mu)$
,
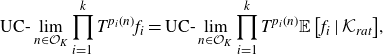 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)} \mathbb{E}\left[ {f_i} \mid {\mathcal{K}_{rat}} \right]}}, \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)} \mathbb{E}\left[ {f_i} \mid {\mathcal{K}_{rat}} \right]}}, \end{align*}
where the limits are taken in
![]() $L^2(\mu)$
.
$L^2(\mu)$
.
Theorem D.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $p(x) \in K[x]$
be a non-constant
$p(x) \in K[x]$
be a non-constant
![]() $\mathcal{O}_K$
-valued polynomial. Then for any ergodic measure-preserving
$\mathcal{O}_K$
-valued polynomial. Then for any ergodic measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
, any
$\left( X, \mathcal{B}, \mu, T \right)$
, any
![]() $l_1, \dots, l_k \in \mathcal{O}_K$
distinct and nonzero, and any
$l_1, \dots, l_k \in \mathcal{O}_K$
distinct and nonzero, and any
![]() $f_1, \dots, f_k \in L^{\infty}(\mu)$
,
$f_1, \dots, f_k \in L^{\infty}(\mu)$
,
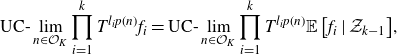 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{l_ip(n)}f_i}} = \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{l_ip(n)} \mathbb{E}\left[ {f_i} \mid {\mathcal{Z}_{k-1}} \right]}}, \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{l_ip(n)}f_i}} = \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{l_ip(n)} \mathbb{E}\left[ {f_i} \mid {\mathcal{Z}_{k-1}} \right]}}, \end{align*}
where the limits are taken in
![]() $L^2(\mu)$
. Moreover, if T is totally ergodic, then this limit does not depend on the polynomial p.
$L^2(\mu)$
. Moreover, if T is totally ergodic, then this limit does not depend on the polynomial p.
We will prove Theorems C and D via equidistribution results for polynomial sequences in nilmanifolds, which are of independent interest (see Theorem 3·3 and Proposition 3·12 below). After several reductions, the main technical result in the proof of Theorem C is the following far-reaching generalisation of Weyl’s polynomial equidistribution theorem for families of independent polynomials in several variables:
Theorem 1·15 (Theorem 3·8). Let
![]() $d, l, k, m \in \mathbb{N}$
. Let
$d, l, k, m \in \mathbb{N}$
. Let
![]() $\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le l\} \subseteq \mathbb{Q}[x_1, \dots, x_d]$
be
$\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le l\} \subseteq \mathbb{Q}[x_1, \dots, x_d]$
be
![]() $\mathbb{Z}$
-valued and independent over
$\mathbb{Z}$
-valued and independent over
![]() $\mathbb{Q}$
. Let
$\mathbb{Q}$
. Let
![]() $T_1, \dots, T_l \;:\; \mathbb{T}^m \to \mathbb{T}^m$
be commuting unipotent affine transformations generating an ergodic
$T_1, \dots, T_l \;:\; \mathbb{T}^m \to \mathbb{T}^m$
be commuting unipotent affine transformations generating an ergodic
![]() $\mathbb{Z}^l$
-action. Then the polynomial sequence
$\mathbb{Z}^l$
-action. Then the polynomial sequence
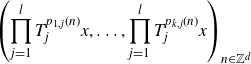 \begin{align*} \left( \prod_{j=1}^l{T_j^{p_{1,j}(n)}}x, \dots, \prod_{j=1}^l{T_j^{p_{k,j}(n)}}x \right)_{n \in \mathbb{Z}^d} \end{align*}
\begin{align*} \left( \prod_{j=1}^l{T_j^{p_{1,j}(n)}}x, \dots, \prod_{j=1}^l{T_j^{p_{k,j}(n)}}x \right)_{n \in \mathbb{Z}^d} \end{align*}
is well-distributed in
![]() $\mathbb{T}^{mk}$
for all x in a co-meager set of full measure.
$\mathbb{T}^{mk}$
for all x in a co-meager set of full measure.
The upshot of Theorem C is that we may compute multiple ergodic averages for independent polynomials by studying the corresponding averages in a finite rotational system, where computations are much easier to carry out. Similarly, Theorem D says that in order to compute multiple ergodic averages for k distinct multiples of a fixed polynomial, we can make use of the algebraic structure of a
![]() $(k-1)$
-step nilsystem.
$(k-1)$
-step nilsystem.
From here, we can follow a standard technique to deduce the corresponding Khintchine-type results. The assumption that the families of polynomials under consideration are jointly intersective, together with a standard approximation argument, allows us to reduce to the case that the action T is totally ergodic, i.e. that
![]() $\mathcal{K}_{rat}$
is trivial. For independent polynomials, Theorem C guarantees that
$\mathcal{K}_{rat}$
is trivial. For independent polynomials, Theorem C guarantees that
for totally ergodic T, from which Theorem A immediately follows. The details of this argument are carried out in Section 4.1. When all of the polynomials involved are multiples of a fixed polynomial and T is totally ergodic, Theorem D says that the relevant multiple ergodic average can be reduced to a linear average (corresponding to
![]() $p(n) = n$
). We are therefore able to capitalise on Khintchine-type results for linear averages (see Theorem 1·9 above) and extend them to the polynomial configurations we consider in Theorem B. The full details of this argument appear in Section 4.2.
$p(n) = n$
). We are therefore able to capitalise on Khintchine-type results for linear averages (see Theorem 1·9 above) and extend them to the polynomial configurations we consider in Theorem B. The full details of this argument appear in Section 4.2.
1·3. Notions of largeness
Syndeticity is just one of many notions of largeness that naturally appear in ergodic theory and combinatorics. While it is useful in quantifying the size of subsets, it does not have all of the properties that one may desire. To illustrate one shortcoming of syndeticity, we return to Szemerédi’s theorem. Consider the family of sets
![]() $\mathcal{R}_k \;:\!=\; \{R_k(\textbf{X}, A) \;:\; \textbf{X} = (X, \mathcal{B}, \mu, T)\;\text{mps}, A \in \mathcal{B}, \mu(A) > 0\}$
, where
$\mathcal{R}_k \;:\!=\; \{R_k(\textbf{X}, A) \;:\; \textbf{X} = (X, \mathcal{B}, \mu, T)\;\text{mps}, A \in \mathcal{B}, \mu(A) > 0\}$
, where
The family
![]() $\mathcal{R}_k$
has the filter property: for any
$\mathcal{R}_k$
has the filter property: for any
![]() $R, S \in \mathcal{R}_k$
, we have
$R, S \in \mathcal{R}_k$
, we have
![]() $R \cap S \ne \emptyset$
. Indeed, given two measure-preserving systems
$R \cap S \ne \emptyset$
. Indeed, given two measure-preserving systems
![]() $\textbf{X} = (X, \mathcal{B}, \mu, T)$
and
$\textbf{X} = (X, \mathcal{B}, \mu, T)$
and
![]() $\textbf{Y} = (Y, \mathcal{D}, \nu, S)$
, one can form the product system
$\textbf{Y} = (Y, \mathcal{D}, \nu, S)$
, one can form the product system
![]() $\textbf{X} \times \textbf{Y}$
and easily verify that
$\textbf{X} \times \textbf{Y}$
and easily verify that
One may hope that there is a different notion of largeness that captures this filter property. To discuss one such notion, we introduce the class of IP sets.
Let
![]() $(x_n)_{n \in \mathbb{N}}$
be a sequence in
$(x_n)_{n \in \mathbb{N}}$
be a sequence in
![]() $\mathcal{O}_K$
. The finite sum set associated to
$\mathcal{O}_K$
. The finite sum set associated to
![]() $(x_n)_{n \in \mathbb{N}}$
is the set
$(x_n)_{n \in \mathbb{N}}$
is the set
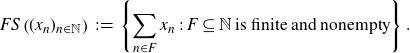 \begin{align*} FS\left( (x_n)_{n \in \mathbb{N}} \right) \;:\!=\; \left\{ \sum_{n \in F}{x_n} \;:\; F \subseteq \mathbb{N}\;\text{is finite and nonempty} \right\}.\end{align*}
\begin{align*} FS\left( (x_n)_{n \in \mathbb{N}} \right) \;:\!=\; \left\{ \sum_{n \in F}{x_n} \;:\; F \subseteq \mathbb{N}\;\text{is finite and nonempty} \right\}.\end{align*}
We say that
![]() $A \subseteq \mathcal{O}_K$
is an IP set if
$A \subseteq \mathcal{O}_K$
is an IP set if
![]() $A \supseteq FS\left( (x_n)_{n \in \mathbb{N}} \right)$
for some infinite sequence
$A \supseteq FS\left( (x_n)_{n \in \mathbb{N}} \right)$
for some infinite sequence
![]() $(x_n)_{n \in \mathbb{N}}$
. A theorem of Hindman [
Reference Hindman28
] asserts that IP sets are partition regular:
$(x_n)_{n \in \mathbb{N}}$
. A theorem of Hindman [
Reference Hindman28
] asserts that IP sets are partition regular:
Theorem 1·16 (Hindman’s Theorem [
Reference Hindman28
, theorem 3·1]). Let A be an IP set. If A is finitely partitioned
![]() $A = \bigcup_{i=1}^r{C_i}$
, then for some
$A = \bigcup_{i=1}^r{C_i}$
, then for some
![]() $i_0 \in \{1, \dots, r\}$
,
$i_0 \in \{1, \dots, r\}$
,
![]() $C_{i_0}$
is an IP set.
$C_{i_0}$
is an IP set.
A set E is
![]() $\text{IP}^*$
if
$\text{IP}^*$
if
![]() $E \cap A \ne \emptyset$
for every IP set A. It follows from Theorem 1·16 that
$E \cap A \ne \emptyset$
for every IP set A. It follows from Theorem 1·16 that
![]() $\text{IP}^*$
sets have the filter property. From this point of view, the IP polynomial Szemerédi theorem is more satisfactory:
$\text{IP}^*$
sets have the filter property. From this point of view, the IP polynomial Szemerédi theorem is more satisfactory:
Theorem 1·17 ([
Reference Bergelson and McCutcheon13
, theorem 0·7]). Let
![]() $p_1, \dots, p_k \in \mathbb{Q}[x]$
be integer-valued polynomials with zero constant term. Then for any ergodic invertible probability measure-preserving system and any
$p_1, \dots, p_k \in \mathbb{Q}[x]$
be integer-valued polynomials with zero constant term. Then for any ergodic invertible probability measure-preserving system and any
![]() $A \in \mathcal{B}$
, the set
$A \in \mathcal{B}$
, the set
is
![]() $\text{IP}^*$
.
$\text{IP}^*$
.
Remark 1·18. For the linear pattern
![]() $p_i(n) = in$
, Theorem 1·17 follows from [
Reference Furstenberg and Katznelson23
, theorem A].
$p_i(n) = in$
, Theorem 1·17 follows from [
Reference Furstenberg and Katznelson23
, theorem A].
When bounding the size of the intersections from below, the filter property is no longer a straightforward consequence from considering product systems. Furthermore,
![]() $\text{IP}^*$
turns out to be too strong of a notion of largeness. (Indeed, in a skew-product system on the torus
$\text{IP}^*$
turns out to be too strong of a notion of largeness. (Indeed, in a skew-product system on the torus
![]() $\mathbb{T}^2$
, one can find a set A for which the set (1·1) fails to be
$\mathbb{T}^2$
, one can find a set A for which the set (1·1) fails to be
![]() $\text{IP}^*$
for small
$\text{IP}^*$
for small
![]() $\varepsilon > 0$
.) However, we can use a slightly weaker notion that retains the filter property. Define the upper Banach density of a set
$\varepsilon > 0$
.) However, we can use a slightly weaker notion that retains the filter property. Define the upper Banach density of a set
![]() $E \subseteq \mathcal{O}_K$
by
$E \subseteq \mathcal{O}_K$
by
We say that E is almost
![]() $\text{IP}^*$
, or
$\text{IP}^*$
, or
![]() $\text{AIP}^*$
for short, if E can be written as
$\text{AIP}^*$
for short, if E can be written as
![]() $E = A \setminus B$
, where A is an
$E = A \setminus B$
, where A is an
![]() $\text{IP}^*$
set and B is a set with
$\text{IP}^*$
set and B is a set with
![]() $d^*(B) = 0$
. In [
Reference Bergelson and Robertson14
], it was shown that the set (1·3) in Theorem 1·7 is in fact a shift of an
$d^*(B) = 0$
. In [
Reference Bergelson and Robertson14
], it was shown that the set (1·3) in Theorem 1·7 is in fact a shift of an
![]() $\text{AIP}^*$
set.
$\text{AIP}^*$
set.
In a similar vein, Theorem 1·3 was strengthened in [
Reference Bergelson and Leibman9
]. There, the notion of largeness used is the even stronger notion of
![]() $\text{AVIP}_0^*$
, which we define in Section 5.
$\text{AVIP}_0^*$
, which we define in Section 5.
Theorem 1·19 ([
Reference Bergelson and Leibman9
, theorem 4·2]). Let
![]() $p_1, \dots, p_k \in \mathbb{Q}[x]$
be linearly independent integer-valued polynomials with zero constant term. Then for any ergodic invertible probability measure-preserving system, any
$p_1, \dots, p_k \in \mathbb{Q}[x]$
be linearly independent integer-valued polynomials with zero constant term. Then for any ergodic invertible probability measure-preserving system, any
![]() $A \in \mathcal{B}$
, and any
$A \in \mathcal{B}$
, and any
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is
![]() $\text{AVIP}_0^*$
.
$\text{AVIP}_0^*$
.
In Section 5, we similarly strengthen the conclusions of Theorem A and Theorem B. In particular, we show that, if T is ergodic, then the sets (1·4), (1·5) and (1·6) are shifts of
![]() $\text{AVIP}_0^*$
sets (see Theorem 5·6 and Theorem 5·7).
$\text{AVIP}_0^*$
sets (see Theorem 5·6 and Theorem 5·7).
1·4. Combinatorial applications
We deduce several combinatorial facts from the ergodic-theoretic theorems above. For some of the combinatorial results, we have stronger finitary versions. For other combinatorial facts derived from ergodic-theoretic results under the assumption of ergodicity, we cannot easily deduce finitary consequences. This distinction arises from subtleties in Furstenberg’s correspondence principle, which we discuss in more detail below. The first version of Furstenberg’s correspondence principle that we will use is as follows:
Theorem 1·20 ([
Reference Bergelson4
, theorem 4·17]). Fix a Følner sequence
![]() $\Phi = (\Phi_N)_{N \in \mathbb{N}}$
in
$\Phi = (\Phi_N)_{N \in \mathbb{N}}$
in
![]() $\mathcal{O}_K$
. Suppose
$\mathcal{O}_K$
. Suppose
![]() $E \subseteq \mathcal{O}_K$
has positive upper density along
$E \subseteq \mathcal{O}_K$
has positive upper density along
![]() $\Phi$
, i.e.
$\Phi$
, i.e.
![]() $\overline{d}_{\Phi}(E) \;:\!=\; \limsup_{N \to \infty}{{|E \cap \Phi_N|}/{|\Phi_N|}} > 0$
. Then there exists an
$\overline{d}_{\Phi}(E) \;:\!=\; \limsup_{N \to \infty}{{|E \cap \Phi_N|}/{|\Phi_N|}} > 0$
. Then there exists an
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $(X, \mathcal{B}, \mu, T)$
and a set
$(X, \mathcal{B}, \mu, T)$
and a set
![]() $A \in \mathcal{B}$
with
$A \in \mathcal{B}$
with
![]() $\mu(A) = \overline{d}_{\Phi}(E)$
such that, for any
$\mu(A) = \overline{d}_{\Phi}(E)$
such that, for any
![]() $k \in \mathbb{N}$
and any
$k \in \mathbb{N}$
and any
![]() $n_1, \dots, n_k \in \mathcal{O}_K$
, one has
$n_1, \dots, n_k \in \mathcal{O}_K$
, one has
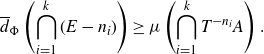 \begin{align} \overline{d}_{\Phi} \left( \bigcap_{i=1}^k{(E - n_i)} \right) \ge \mu \left( \bigcap_{i=1}^k{T^{-n_i}A} \right). \end{align}
\begin{align} \overline{d}_{\Phi} \left( \bigcap_{i=1}^k{(E - n_i)} \right) \ge \mu \left( \bigcap_{i=1}^k{T^{-n_i}A} \right). \end{align}
Applying Theorem 1·20 directly alongside Theorem A, we get the following:
Theorem 1·21.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
$\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
![]() $\mathcal{O}_K$
-valued polynomials. Fix a Følner sequence
$\mathcal{O}_K$
-valued polynomials. Fix a Følner sequence
![]() $\Phi = (\Phi_N)_{N \in \mathbb{N}}$
and suppose
$\Phi = (\Phi_N)_{N \in \mathbb{N}}$
and suppose
![]() $E \subseteq \mathcal{O}_K$
satisfies
$E \subseteq \mathcal{O}_K$
satisfies
![]() $\overline{d}_{\Phi}(E) > 0$
. Then for any
$\overline{d}_{\Phi}(E) > 0$
. Then for any
![]() $\varepsilon > 0$
,
$\varepsilon > 0$
,
is syndetic.
Taking the natural Følner sequence
![]() $\Phi_N = \{1, \dots, N\}^d$
under the isomorphism
$\Phi_N = \{1, \dots, N\}^d$
under the isomorphism
![]() $\mathcal{O}_K \cong \mathbb{Z}^d$
, we deduce a related finitary result:
$\mathcal{O}_K \cong \mathbb{Z}^d$
, we deduce a related finitary result:
Corollary 1·22.
Let K be a degree d number field with ring of integers
![]() $\mathcal{O}_K \cong \mathbb{Z}^d$
. Let
$\mathcal{O}_K \cong \mathbb{Z}^d$
. Let
![]() $\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
$\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
![]() $\mathcal{O}_K$
-valued polynomials. For any
$\mathcal{O}_K$
-valued polynomials. For any
![]() $\delta, \varepsilon > 0$
, there exists
$\delta, \varepsilon > 0$
, there exists
![]() $N = N(\delta, \varepsilon) \in \mathbb{N}$
such that: if
$N = N(\delta, \varepsilon) \in \mathbb{N}$
such that: if
![]() $A \subseteq \{1, \dots, N\}^d$
with
$A \subseteq \{1, \dots, N\}^d$
with
![]() $|A| > \delta N^d$
, then A contains at least
$|A| > \delta N^d$
, then A contains at least
![]() $(\delta^{k+1} - \varepsilon)N^d$
configurations of the form
$(\delta^{k+1} - \varepsilon)N^d$
configurations of the form
![]() $\{x, x + p_1(n), \dots, x + p_k(n)\}$
for some
$\{x, x + p_1(n), \dots, x + p_k(n)\}$
for some
![]() $n \ne 0$
.
$n \ne 0$
.
Proof. Let
![]() $\delta, \varepsilon > 0$
, and suppose no such N exists. That is, for some sequence
$\delta, \varepsilon > 0$
, and suppose no such N exists. That is, for some sequence
![]() $N_m \to \infty$
, we can find sets
$N_m \to \infty$
, we can find sets
![]() $A_m \subseteq \{1, \dots, N\}^d$
with
$A_m \subseteq \{1, \dots, N\}^d$
with
![]() $|A_m| > \delta N_m^d$
such that
$|A_m| > \delta N_m^d$
such that
for every
![]() $n \ne 0$
.
$n \ne 0$
.
By passing to a subsequence if necessary, we may assume
exists for all
![]() $r \in \mathbb{N}$
,
$r \in \mathbb{N}$
,
![]() $n_1, \dots, n_r \in \mathcal{O}_K$
, and
$n_1, \dots, n_r \in \mathcal{O}_K$
, and
![]() $i_1, \dots, i_r \in \{0, 1\}$
, where
$i_1, \dots, i_r \in \{0, 1\}$
, where
![]() $A_{m,0} = A_m$
and
$A_{m,0} = A_m$
and
![]() $A_{m,1} = \mathcal{O}_K \setminus A_m$
. Then we may define a measure on
$A_{m,1} = \mathcal{O}_K \setminus A_m$
. Then we may define a measure on
![]() $X = \{0,1\}^{\mathcal{O}_K}$
by letting
$X = \{0,1\}^{\mathcal{O}_K}$
by letting
and extending using Kolmogorov’s extension theorem. Note that the shift map
![]() $(T^nx)(m) = x(n+m)$
preserves the measure
$(T^nx)(m) = x(n+m)$
preserves the measure
![]() $\mu$
. Taking
$\mu$
. Taking
![]() $A = \{x \in X \;:\; x_0 = 1\}$
, we have
$A = \{x \in X \;:\; x_0 = 1\}$
, we have
and on the other hand,
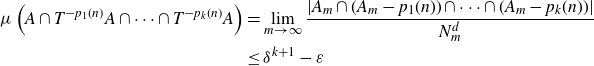 \begin{align*} \mu \left( A \cap T^{-p_1(n)}A \cap \dots \cap T^{-p_k(n)}A \right) & = \lim_{m \to \infty}{\frac{\left| A_m \cap (A_m - p_1(n)) \cap \dots \cap (A_m - p_k(n)) \right|}{N_m^d}} \\ & \le \delta^{k+1} - \varepsilon \end{align*}
\begin{align*} \mu \left( A \cap T^{-p_1(n)}A \cap \dots \cap T^{-p_k(n)}A \right) & = \lim_{m \to \infty}{\frac{\left| A_m \cap (A_m - p_1(n)) \cap \dots \cap (A_m - p_k(n)) \right|}{N_m^d}} \\ & \le \delta^{k+1} - \varepsilon \end{align*}
for
![]() $n \ne 0$
. This contradicts Theorem A.
$n \ne 0$
. This contradicts Theorem A.
Note that the system in Theorem 1·20 may not be ergodic. To obtain an inequality similar to (1·8) while ensuring that the system is ergodic, one needs to allow for replacing the density along
![]() $\Phi$
by the density along some other Følner sequence depending on the choice of translates
$\Phi$
by the density along some other Følner sequence depending on the choice of translates
![]() $n_1, \dots, n_k$
. (An example due to Hindman [
Reference Hindman29
] can be used to show that, for certain sets E, the measure-preserving system in the conclusion of Theorem 1·20 is necessarily non-ergodic; see the discussion following theorem 1·3 in [
Reference Bergelson and Ferré Moragues5
] for more detail.) Using the notion of upper Banach density, we can formulate an ergodic version of Furstenberg’s correspondence principle:
$n_1, \dots, n_k$
. (An example due to Hindman [
Reference Hindman29
] can be used to show that, for certain sets E, the measure-preserving system in the conclusion of Theorem 1·20 is necessarily non-ergodic; see the discussion following theorem 1·3 in [
Reference Bergelson and Ferré Moragues5
] for more detail.) Using the notion of upper Banach density, we can formulate an ergodic version of Furstenberg’s correspondence principle:
Theorem 1·23.
Suppose
![]() $E \subseteq \mathcal{O}_K$
has positive upper Banach density. Then there exists an ergodic
$E \subseteq \mathcal{O}_K$
has positive upper Banach density. Then there exists an ergodic
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $(X, \mathcal{B}, \mu, T)$
and a set
$(X, \mathcal{B}, \mu, T)$
and a set
![]() $A \in \mathcal{B}$
with
$A \in \mathcal{B}$
with
![]() $\mu(A) = d^*(E)$
such that, for any
$\mu(A) = d^*(E)$
such that, for any
![]() $k \in \mathbb{N}$
and any
$k \in \mathbb{N}$
and any
![]() $n_1, \dots, n_k \in \mathcal{O}_K$
, one has
$n_1, \dots, n_k \in \mathcal{O}_K$
, one has
 \begin{align*} d^* \left( \bigcap_{i=1}^k{(E - n_i)} \right) \ge \mu \left( \bigcap_{i=1}^k{T^{-n_i}A} \right). \end{align*}
\begin{align*} d^* \left( \bigcap_{i=1}^k{(E - n_i)} \right) \ge \mu \left( \bigcap_{i=1}^k{T^{-n_i}A} \right). \end{align*}
For
![]() $\mathbb{Z}$
-actions, Theorem 1·23 appears in [
Reference Bergelson6
, proposition 3·1], utilising an observation of Emmanuel Lesigne based on the original argument of Furstenberg. For a general version in amenable groups (a class containing all countable abelian groups), see [
Reference Bergelson and Ferré Moragues5
, theorem 2·8].
$\mathbb{Z}$
-actions, Theorem 1·23 appears in [
Reference Bergelson6
, proposition 3·1], utilising an observation of Emmanuel Lesigne based on the original argument of Furstenberg. For a general version in amenable groups (a class containing all countable abelian groups), see [
Reference Bergelson and Ferré Moragues5
, theorem 2·8].
As a consequence, we obtain the following combinatorial version of Theorem 5·7:
Theorem 1·24.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $p(x) \in K[x]$
be an
$p(x) \in K[x]$
be an
![]() $\mathcal{O}_K$
-valued intersective polynomial. Let
$\mathcal{O}_K$
-valued intersective polynomial. Let
![]() $r,s \in \mathcal{O}_K$
be distinct and nonzero. Then for any set
$r,s \in \mathcal{O}_K$
be distinct and nonzero. Then for any set
![]() $E \subseteq \mathcal{O}_K$
with
$E \subseteq \mathcal{O}_K$
with
![]() $d^*(E) > 0$
and any
$d^*(E) > 0$
and any
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is
![]() $\text{AVIP}_{0,+}^*$
(in particular, it is syndetic).
$\text{AVIP}_{0,+}^*$
(in particular, it is syndetic).
Moreover, if
![]() $\frac{s}{r} \in \mathbb{Q}$
, then
$\frac{s}{r} \in \mathbb{Q}$
, then
is
![]() $\text{AVIP}_{0,+}^*$
(in particular, it is syndetic).
$\text{AVIP}_{0,+}^*$
(in particular, it is syndetic).
As discussed above, the ergodicity assumption in Theorems B and 5·7 precludes us from easily deducing finitary results along the lines of Corollary 1·22. Nevertheless, we suspect that a finitary analogue holds, which we formulate below:
Conjecture 1·25.
Let K be a degree d number field with ring of integers
![]() $\mathcal{O}_K \cong \mathbb{Z}^d$
. Suppose
$\mathcal{O}_K \cong \mathbb{Z}^d$
. Suppose
![]() $p(x) \in K[x]$
is an
$p(x) \in K[x]$
is an
![]() $\mathcal{O}_K$
-valued intersective polynomial.
$\mathcal{O}_K$
-valued intersective polynomial.
-
(1) let
 $r, s \in \mathcal{O}_K$
be distinct and nonzero. For any
$r, s \in \mathcal{O}_K$
be distinct and nonzero. For any
 $\delta, \varepsilon > 0$
, there exists
$\delta, \varepsilon > 0$
, there exists
 $N = N(\varepsilon, \delta) \in \mathbb{N}$
such that: if
$N = N(\varepsilon, \delta) \in \mathbb{N}$
such that: if
 $A \subseteq \{1, \dots, N\}^d$
with
$A \subseteq \{1, \dots, N\}^d$
with
 $|A| > \delta N^d$
, then A contains at least
$|A| > \delta N^d$
, then A contains at least
 $(\delta^3 - \varepsilon)N^d$
configurations of the form
$(\delta^3 - \varepsilon)N^d$
configurations of the form
 $\{x, x + rp(n), x + sp(n)\}$
for some
$\{x, x + rp(n), x + sp(n)\}$
for some
 $n \ne 0$
.
$n \ne 0$
. -
(2) let
 $r, s \in \mathcal{O}_K$
be distinct and nonzero such that
$r, s \in \mathcal{O}_K$
be distinct and nonzero such that
 ${s}/{r} \in \mathbb{Q}$
(or more generally, no two conjugates of
${s}/{r} \in \mathbb{Q}$
(or more generally, no two conjugates of
 $\frac{s}{r}$
are negatives of each other). For any
$\frac{s}{r}$
are negatives of each other). For any
 $\delta, \varepsilon > 0$
, there exists
$\delta, \varepsilon > 0$
, there exists
 $N = N(\varepsilon, \delta) \in \mathbb{N}$
such that: if
$N = N(\varepsilon, \delta) \in \mathbb{N}$
such that: if
 $A \subseteq \{1, \dots, N\}^d$
with
$A \subseteq \{1, \dots, N\}^d$
with
 $|A| > \delta N^d$
, then A contains at least
$|A| > \delta N^d$
, then A contains at least
 $(\delta^4 - \varepsilon)N^d$
configurations of the form
$(\delta^4 - \varepsilon)N^d$
configurations of the form
 $\{x, x + rp(n), x + sp(n), x + rp(n) + sp(n)\}$
for some
$\{x, x + rp(n), x + sp(n), x + rp(n) + sp(n)\}$
for some
 $n \ne 0$
.
$n \ne 0$
.
In the simplest case when
![]() $K = \mathbb{Q}$
and
$K = \mathbb{Q}$
and
![]() $p(n) = n$
, Conjecture 1·25 was posed as a question in [
Reference Bergelson6
] and verified in [
Reference Green25
, theorem 1·10] and [
Reference Green and Tao26
, theorem 1·12]. For more general linear patterns (the case
$p(n) = n$
, Conjecture 1·25 was posed as a question in [
Reference Bergelson6
] and verified in [
Reference Green25
, theorem 1·10] and [
Reference Green and Tao26
, theorem 1·12]. For more general linear patterns (the case
![]() $p(n) = n$
), closely related finitary results were recently established in [
Reference Berger, Sah, Sawhney and Tidor16, 32
].
$p(n) = n$
), closely related finitary results were recently established in [
Reference Berger, Sah, Sawhney and Tidor16, 32
].
1·5. Outline of the paper
The structure of the paper is as follows. In Section 2, we collect several useful facts that will be used repeatedly in the proofs of the main theorems. Section 3 is devoted to proving Theorems C and D on characteristic factors corresponding to the polynomial configurations of interest via equidistribution results on nilmanifolds. Using the knowledge of characteristic factors, we prove Khintchine-type results (Theorems A and B in Section 4. Finally, Section 5 handles the refinements of our Khintchine-type theorems to conclude stronger combinatorial properties about the abundance of combinatorial configurations.
2. Preliminaries
2·1. Rational Kronecker factor
Recall that the Kronecker factor for an ergodic measure-preserving system is spanned by eigenfunctions. As suggested by the name, the rational Kronecker factor will be spanned by eigenfunctions with rational eigenvalues. To make this precise, we need to define what it means for an eigenvalue (a group character) to be rational.
Since the additive group structure for the ring of integers in a degree d extension of
![]() $\mathbb{Q}$
is
$\mathbb{Q}$
is
![]() $\mathbb{Z}^d$
, we say that a character
$\mathbb{Z}^d$
, we say that a character
![]() $\chi \;:\; \mathbb{Z}^d \to \mathbb{T}$
is rational if there is an element
$\chi \;:\; \mathbb{Z}^d \to \mathbb{T}$
is rational if there is an element
![]() $(q_1, \dots, q_d) \in \mathbb{Q}^d$
such that
$(q_1, \dots, q_d) \in \mathbb{Q}^d$
such that
For notational convenience, we will let
![]() $e \;:\; \mathbb{R} \to \mathbb{T}$
be the function
$e \;:\; \mathbb{R} \to \mathbb{T}$
be the function
![]() $e(x) = e^{2\pi ix}$
so that we can write equation (2·1) in the more compact form
$e(x) = e^{2\pi ix}$
so that we can write equation (2·1) in the more compact form
for the usual dot product
![]() $\cdot$
on
$\cdot$
on
![]() $\mathbb{R}^d$
.
$\mathbb{R}^d$
.
The property of rational characters that we will utilise later on is periodicity. Given a number field K with ring of integers
![]() $\mathcal{O}_K$
, we say that a character
$\mathcal{O}_K$
, we say that a character
![]() $\chi \;:\; \mathcal{O}_K \to \mathbb{T}$
is periodic, with period
$\chi \;:\; \mathcal{O}_K \to \mathbb{T}$
is periodic, with period
![]() $p \in \mathcal{O}_K$
, if for all
$p \in \mathcal{O}_K$
, if for all
![]() $n, m \in \mathcal{O}_K$
, we have
$n, m \in \mathcal{O}_K$
, we have
To translate this back into language where rationality makes sense, take an integral basis
![]() $\{b_1, \dots, b_d\}$
so that
$\{b_1, \dots, b_d\}$
so that
![]() $(\mathcal{O}_K,+) \cong \bigoplus_{i=1}^d{\mathbb{Z} \cdot b_i}$
. Since
$(\mathcal{O}_K,+) \cong \bigoplus_{i=1}^d{\mathbb{Z} \cdot b_i}$
. Since
![]() $\widehat{\mathbb{Z}^d} \cong \mathbb{T}^d$
, there is an element
$\widehat{\mathbb{Z}^d} \cong \mathbb{T}^d$
, there is an element
![]() $\alpha \in \mathbb{T}^d$
so that
$\alpha \in \mathbb{T}^d$
so that
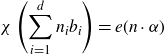 \begin{align*} \chi \left( \sum_{i=1}^d{n_ib_i} \right) = e(n \cdot \alpha)\end{align*}
\begin{align*} \chi \left( \sum_{i=1}^d{n_ib_i} \right) = e(n \cdot \alpha)\end{align*}
for
![]() $n \in \mathbb{Z}^d$
. We can then say that
$n \in \mathbb{Z}^d$
. We can then say that
![]() $\chi \;:\; \mathcal{O}_K \to \mathbb{T}$
is rational if
$\chi \;:\; \mathcal{O}_K \to \mathbb{T}$
is rational if
![]() $\alpha \in \mathbb{Q}^d/\mathbb{Z}^d$
. We now show that rationality and periodicity coincide:
$\alpha \in \mathbb{Q}^d/\mathbb{Z}^d$
. We now show that rationality and periodicity coincide:
Lemma 2·1.
A character
![]() $\chi \;:\; \mathcal{O}_K \to \mathbb{T}$
is rational if and only if it is periodic.
$\chi \;:\; \mathcal{O}_K \to \mathbb{T}$
is rational if and only if it is periodic.
Proof. Suppose
![]() $\chi$
is rational, say
$\chi$
is rational, say
![]() $\chi(n) = e(n \cdot q)$
with
$\chi(n) = e(n \cdot q)$
with
![]() $q = (q_1, \dots, q_d) \in \mathbb{Q}^d$
. Choose
$q = (q_1, \dots, q_d) \in \mathbb{Q}^d$
. Choose
![]() $D \in \mathbb{Z}$
so that
$D \in \mathbb{Z}$
so that
![]() $Dq_i \in \mathbb{Z}$
for every
$Dq_i \in \mathbb{Z}$
for every
![]() $i = 1, \dots, d$
, and set
$i = 1, \dots, d$
, and set
![]() $p \;:\!=\; D \left( \sum_{i=1}^d{b_i} \right)$
. We claim that p is a period for
$p \;:\!=\; D \left( \sum_{i=1}^d{b_i} \right)$
. We claim that p is a period for
![]() $\chi$
. Indeed, given
$\chi$
. Indeed, given
![]() $m = \sum_{i=1}^d{m_i b_i} \in \mathcal{O}_K$
, we have
$m = \sum_{i=1}^d{m_i b_i} \in \mathcal{O}_K$
, we have
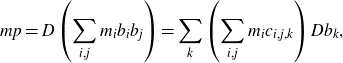 \begin{align*} mp = D \left( \sum_{i,j}{m_i b_i b_j} \right) = \sum_k{\left( \sum_{i,j}{m_i c_{i,j,k}} \right) D b_k}, \end{align*}
\begin{align*} mp = D \left( \sum_{i,j}{m_i b_i b_j} \right) = \sum_k{\left( \sum_{i,j}{m_i c_{i,j,k}} \right) D b_k}, \end{align*}
where
![]() $c_{i,j,k} \in \mathbb{Z}$
so that
$c_{i,j,k} \in \mathbb{Z}$
so that
![]() $b_ib_j = \sum_k{c_{i,j,k}b_k}$
. Hence,
$b_ib_j = \sum_k{c_{i,j,k}b_k}$
. Hence,
![]() $mp \cdot q = \sum_k{\left( \sum_{i,j}{m_i c_{i,j,k}} \right) D q_k} \in \mathbb{Z}$
, so
$mp \cdot q = \sum_k{\left( \sum_{i,j}{m_i c_{i,j,k}} \right) D q_k} \in \mathbb{Z}$
, so
![]() $\chi(mp) = e(mp \cdot q) = 1$
for every
$\chi(mp) = e(mp \cdot q) = 1$
for every
![]() $m \in \mathcal{O}_K$
.
$m \in \mathcal{O}_K$
.
Conversely, suppose
![]() $\chi$
is periodic with period
$\chi$
is periodic with period
![]() $p \in \mathcal{O}_K$
. Let
$p \in \mathcal{O}_K$
. Let
![]() $\alpha \in \mathbb{T}^d$
such that
$\alpha \in \mathbb{T}^d$
such that
![]() $\chi(n) = e(n \cdot \alpha)$
. Since
$\chi(n) = e(n \cdot \alpha)$
. Since
![]() $\{b_1, \dots, b_d\}$
is a
$\{b_1, \dots, b_d\}$
is a
![]() $\mathbb{Q}$
-basis for K, we can write
$\mathbb{Q}$
-basis for K, we can write
![]() ${1}/{p} = \sum_{i=1}^d{a_ib_i}$
for some
${1}/{p} = \sum_{i=1}^d{a_ib_i}$
for some
![]() $a_1, \dots, a_d \in \mathbb{Q}$
. Let
$a_1, \dots, a_d \in \mathbb{Q}$
. Let
![]() $D \in \mathbb{Z}$
such that
$D \in \mathbb{Z}$
such that
![]() $Da_i \in \mathbb{Z}$
for every
$Da_i \in \mathbb{Z}$
for every
![]() $i = 1, \dots, d$
. Then
$i = 1, \dots, d$
. Then
![]() ${D}/{p}$
is a
${D}/{p}$
is a
![]() $\mathbb{Z}$
-linear combination of basis elements, so
$\mathbb{Z}$
-linear combination of basis elements, so
![]() $\frac{D}{p} \in \mathcal{O}_K$
. Now let
$\frac{D}{p} \in \mathcal{O}_K$
. Now let
![]() $m_i = {D}{p}/ b_i \in \mathcal{O}_K$
. Since
$m_i = {D}{p}/ b_i \in \mathcal{O}_K$
. Since
![]() $\chi$
is p-periodic, we have
$\chi$
is p-periodic, we have
That is,
![]() $D\alpha_i \in \mathbb{Z}$
, so
$D\alpha_i \in \mathbb{Z}$
, so
![]() $\alpha_i \in \mathbb{Q}$
for all
$\alpha_i \in \mathbb{Q}$
for all
![]() $i = 1, \dots, d$
. Thus,
$i = 1, \dots, d$
. Thus,
![]() $\chi$
is rational.
$\chi$
is rational.
Now we can give our definition:
Definition 2·2. Let K be a number field, and let
![]() $\mathcal{O}_K$
be its ring of integers. Let
$\mathcal{O}_K$
be its ring of integers. Let
![]() $\textbf{X} = \left( X, \mathcal{B}, \mu, T \right)$
be an ergodic
$\textbf{X} = \left( X, \mathcal{B}, \mu, T \right)$
be an ergodic
![]() $\mathcal{O}_K$
-system. The rational Kronecker factor of
$\mathcal{O}_K$
-system. The rational Kronecker factor of
![]() $\textbf{X}$
, denoted by
$\textbf{X}$
, denoted by
![]() $\mathcal{K}_{rat}(\textbf{X})$
, is the factor generated by the algebra
$\mathcal{K}_{rat}(\textbf{X})$
, is the factor generated by the algebra
Building on Lemma 2·1, we can characterize total ergodicity in several equivalent ways:
Proposition 2·3.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\textbf{X} = (X, \mathcal{B}, \mu, T)$
be an ergodic
$\textbf{X} = (X, \mathcal{B}, \mu, T)$
be an ergodic
![]() $\mathcal{O}_K$
-system. The following are equivalent:
$\mathcal{O}_K$
-system. The following are equivalent:
-
(i) the rational Kronecker factor
 $\mathcal{K}_{rat}(\textbf{X})$
is trivial;
$\mathcal{K}_{rat}(\textbf{X})$
is trivial;
-
(ii) for every
 $r \in \mathcal{O}_K \setminus \{0\}$
,
$r \in \mathcal{O}_K \setminus \{0\}$
,
 $(T^{rn})_{n \in \mathcal{O}_K}$
is ergodic;
$(T^{rn})_{n \in \mathcal{O}_K}$
is ergodic;
-
(iii) for every finite index subgroup
 $\Lambda \subseteq (\mathcal{O}_K, +)$
, the action
$\Lambda \subseteq (\mathcal{O}_K, +)$
, the action
 $(T^n)_{n \in \Lambda}$
is ergodic.
$(T^n)_{n \in \Lambda}$
is ergodic.
Proof. Since
![]() $r\mathcal{O}_K$
has finite index in
$r\mathcal{O}_K$
has finite index in
![]() $\mathcal{O}_K$
, we trivially have the implication (iii)
$\mathcal{O}_K$
, we trivially have the implication (iii)
![]() $\implies$
(ii). We will show (i)
$\implies$
(ii). We will show (i)
![]() $\implies$
(iii) and (ii)
$\implies$
(iii) and (ii)
![]() $\implies$
(i).
$\implies$
(i).
-
(i)
 $\implies$
(iii). Suppose
$\implies$
(iii). Suppose
 $\mathcal{K}_{rat}(\textbf{X})$
is trivial. Let
$\mathcal{K}_{rat}(\textbf{X})$
is trivial. Let
 $\Lambda \subseteq (\mathcal{O}_K,+)$
be a finite index subgroup, and suppose
$\Lambda \subseteq (\mathcal{O}_K,+)$
be a finite index subgroup, and suppose
 $T^nf = f$
for every
$T^nf = f$
for every
 $n \in \Lambda$
. Then the orbit
$n \in \Lambda$
. Then the orbit
 $\{T^nf \;:\; n \in \mathcal{O}_K\}$
is finite: it consists of the elements
$\{T^nf \;:\; n \in \mathcal{O}_K\}$
is finite: it consists of the elements
 $T^mf$
for m in a finite set F satisfying
$T^mf$
for m in a finite set F satisfying
 $\Lambda + F = \mathcal{O}_K$
. In particular, the orbit is (pre-)compact, so f is a linear combination of eigenfunctions,
$\Lambda + F = \mathcal{O}_K$
. In particular, the orbit is (pre-)compact, so f is a linear combination of eigenfunctions,
 $f = \sum_i{c_if_i}$
, with
$f = \sum_i{c_if_i}$
, with
 $T^nf_i = \chi_i(n)f_i$
for some characters
$T^nf_i = \chi_i(n)f_i$
for some characters
 $\chi_i \;:\; \mathcal{O}_K \to \mathbb{T}$
. Since
$\chi_i \;:\; \mathcal{O}_K \to \mathbb{T}$
. Since
 $T^nf = f$
for
$T^nf = f$
for
 $n \in \Lambda$
, we have
$n \in \Lambda$
, we have
 $\chi_i(n) = 1$
for
$\chi_i(n) = 1$
for
 $n \in \Lambda$
. Therefore,
$n \in \Lambda$
. Therefore,
 $\chi_i$
takes only the finitely many values
$\chi_i$
takes only the finitely many values
 $\chi_i(m)$
,
$\chi_i(m)$
,
 $m \in F$
. It follows that
$m \in F$
. It follows that
 $\chi_i$
is rational. But
$\chi_i$
is rational. But
 $\mathcal{K}_{rat}(\textbf{X})$
is trivial, so in fact
$\mathcal{K}_{rat}(\textbf{X})$
is trivial, so in fact
 $\chi_i = 1$
. Hence,
$\chi_i = 1$
. Hence,
 $T^nf = f$
for every
$T^nf = f$
for every
 $n \in \mathcal{O}_K$
. Since
$n \in \mathcal{O}_K$
. Since
 $(T^n)_{n \in \mathcal{O}_K}$
is ergodic, we have that f is a constant function. Thus,
$(T^n)_{n \in \mathcal{O}_K}$
is ergodic, we have that f is a constant function. Thus,
 $(T^n)_{n \in \Lambda}$
is ergodic.
$(T^n)_{n \in \Lambda}$
is ergodic. -
(ii)
 $\implies$
(i). We prove the contrapositive. Suppose
$\implies$
(i). We prove the contrapositive. Suppose
 $\mathcal{K}_{rat}(\textbf{X})$
is not trivial. Then there is a non-constant function
$\mathcal{K}_{rat}(\textbf{X})$
is not trivial. Then there is a non-constant function
 $f \in L^2(\mu)$
and a rational character
$f \in L^2(\mu)$
and a rational character
 $\chi \;:\; \mathcal{O}_K \to \mathbb{T}$
such that
$\chi \;:\; \mathcal{O}_K \to \mathbb{T}$
such that
 $T^nf = \chi(n)f$
for
$T^nf = \chi(n)f$
for
 $n \in \mathcal{O}_K$
. By Lemma 2·1,
$n \in \mathcal{O}_K$
. By Lemma 2·1,
 $\chi$
is periodic, say with period p. That is,
$\chi$
is periodic, say with period p. That is,
 $\chi(n+pm) = \chi(n)$
for
$\chi(n+pm) = \chi(n)$
for
 $n, m \in \mathcal{O}_K$
. But then
$n, m \in \mathcal{O}_K$
. But then
 $T^{pn}f = \chi(pn)f = f$
for every
$T^{pn}f = \chi(pn)f = f$
for every
 $n \in \mathcal{O}_K$
. Hence,
$n \in \mathcal{O}_K$
. Hence,
 $(T^{pn})_{n \in \mathbb{N}}$
is not ergodic, so (ii) fails.
$(T^{pn})_{n \in \mathbb{N}}$
is not ergodic, so (ii) fails.
2·2. Nilsystems
Proposition 2·4.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $(X, \mathcal{B}, \mu, T)$
be an ergodic
$(X, \mathcal{B}, \mu, T)$
be an ergodic
![]() $\mathcal{O}_K$
-nilsystem. Then T is totally ergodic if and only if X is connected.
$\mathcal{O}_K$
-nilsystem. Then T is totally ergodic if and only if X is connected.
Proof. Write
![]() $X = G/\Gamma$
. Let
$X = G/\Gamma$
. Let
![]() $a \;:\; \mathcal{O}_K \to G$
be a homomorphism so that
$a \;:\; \mathcal{O}_K \to G$
be a homomorphism so that
![]() $T^nx = a(n) \cdot x$
for
$T^nx = a(n) \cdot x$
for
![]() $n \in \mathcal{O}_K$
and
$n \in \mathcal{O}_K$
and
![]() $x \in X$
. Let
$x \in X$
. Let
![]() $x_0$
denote the image of the identity element in X.
$x_0$
denote the image of the identity element in X.
Suppose T is totally ergodic, and let
![]() $X_0$
be the connected component of
$X_0$
be the connected component of
![]() $x_0$
. Since X is compact, it is a disjoint union of finitely many translates of
$x_0$
. Since X is compact, it is a disjoint union of finitely many translates of
![]() $X_0$
, say
$X_0$
, say
![]() $X = \bigcup_{i=0}^{k-1}{X_i}$
with
$X = \bigcup_{i=0}^{k-1}{X_i}$
with
![]() $X_i = g_iX_0$
. Hence, G permutes the components
$X_i = g_iX_0$
. Hence, G permutes the components
![]() $X_0, \dots, X_{k-1}$
, giving a homomorphism
$X_0, \dots, X_{k-1}$
, giving a homomorphism
![]() $\varphi \;:\; G \to S_k$
, where
$\varphi \;:\; G \to S_k$
, where
![]() $S_k$
is the symmetric group on k symbols. This in turn gives a homomorphism
$S_k$
is the symmetric group on k symbols. This in turn gives a homomorphism
![]() $\omega = \varphi \circ a \;:\; \mathcal{O}_K \to S_k$
. Let
$\omega = \varphi \circ a \;:\; \mathcal{O}_K \to S_k$
. Let
![]() $\Omega = \ker{\omega} \subseteq \mathcal{O}_K$
. Since
$\Omega = \ker{\omega} \subseteq \mathcal{O}_K$
. Since
![]() $S_k$
is a finite group,
$S_k$
is a finite group,
![]() $\Omega$
has finite index in
$\Omega$
has finite index in
![]() $\mathcal{O}_K$
. Therefore,
$\mathcal{O}_K$
. Therefore,
![]() $(T^n)_{n \in \Omega}$
acts ergodically on X (see Proposition 2·3(iii)). In particular,
$(T^n)_{n \in \Omega}$
acts ergodically on X (see Proposition 2·3(iii)). In particular,
![]() $\overline{\{a(n)x_0 \;:\; n \in \Omega\}} = X$
. But for
$\overline{\{a(n)x_0 \;:\; n \in \Omega\}} = X$
. But for
![]() $n \in \Omega$
, we have
$n \in \Omega$
, we have
![]() $a(n)X_i = X_i$
, so
$a(n)X_i = X_i$
, so
![]() $a(n)x_0 \in X_0$
. Thus,
$a(n)x_0 \in X_0$
. Thus,
![]() $X = X_0$
.
$X = X_0$
.
Conversely, suppose X is connected, and let
![]() $r \in \mathcal{O}_K \setminus \{0\}$
. The group
$r \in \mathcal{O}_K \setminus \{0\}$
. The group
![]() $r\mathcal{O}_K$
has finite index in
$r\mathcal{O}_K$
has finite index in
![]() $\mathcal{O}_K$
, so let
$\mathcal{O}_K$
, so let
![]() $s_0, \dots, s_{k-1} \in \mathcal{O}_K$
such that
$s_0, \dots, s_{k-1} \in \mathcal{O}_K$
such that
![]() $\bigcup_{i=0}^{k-1}{(r\mathcal{O}_K + s_i)} = \mathcal{O}_K$
. Let
$\bigcup_{i=0}^{k-1}{(r\mathcal{O}_K + s_i)} = \mathcal{O}_K$
. Let
![]() $Y \;:\!=\; \overline{\{a(rn)x_0 \;:\; n \in \mathcal{O}_K\}}$
. Then by ergodicity of T, we have
$Y \;:\!=\; \overline{\{a(rn)x_0 \;:\; n \in \mathcal{O}_K\}}$
. Then by ergodicity of T, we have
![]() $X = \bigcup_{i=0}^{k-1}{a(s_i)Y}$
. We claim that for
$X = \bigcup_{i=0}^{k-1}{a(s_i)Y}$
. We claim that for
![]() $0 \le i, j \le k-1$
, the sets
$0 \le i, j \le k-1$
, the sets
![]() $a(s_i)Y$
and
$a(s_i)Y$
and
![]() $a(s_j)Y$
are either disjoint or identical. Indeed, suppose
$a(s_j)Y$
are either disjoint or identical. Indeed, suppose
![]() $x \in a(s_i)Y \cap a(s_j)Y$
. Then there are sequences
$x \in a(s_i)Y \cap a(s_j)Y$
. Then there are sequences
![]() $(n_t)_{t \in \mathbb{N}}$
and
$(n_t)_{t \in \mathbb{N}}$
and
![]() $(m_t)_{t \in \mathbb{N}}$
in
$(m_t)_{t \in \mathbb{N}}$
in
![]() $\mathcal{O}_K$
such that
$\mathcal{O}_K$
such that
Let
![]() $(\gamma_t)_{t \in \mathbb{N}}$
and
$(\gamma_t)_{t \in \mathbb{N}}$
and
![]() $(\delta_t)_{t \in \mathbb{N}}$
be sequences in
$(\delta_t)_{t \in \mathbb{N}}$
be sequences in
![]() $\Gamma$
and
$\Gamma$
and
![]() $g \in G$
with
$g \in G$
with
![]() $g\Gamma = x$
so that
$g\Gamma = x$
so that
Then
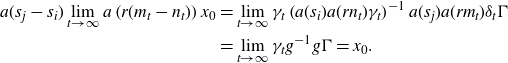 \begin{align*} a(s_j - s_i) \lim_{t \to \infty}{a \left( r (m_t - n_t) \right) x_0} & = \lim_{t \to \infty}{\gamma_t \left( a(s_i) a(rn_t) \gamma_t \right)^{-1} a(s_j) a(rm_t) \delta_t \Gamma} \\ & = \lim_{t \to \infty}{\gamma_t g^{-1} g \Gamma} = x_0. \end{align*}
\begin{align*} a(s_j - s_i) \lim_{t \to \infty}{a \left( r (m_t - n_t) \right) x_0} & = \lim_{t \to \infty}{\gamma_t \left( a(s_i) a(rn_t) \gamma_t \right)^{-1} a(s_j) a(rm_t) \delta_t \Gamma} \\ & = \lim_{t \to \infty}{\gamma_t g^{-1} g \Gamma} = x_0. \end{align*}
It follows that
![]() $a(s_j-s_i)Y = Y$
, so multiplying by
$a(s_j-s_i)Y = Y$
, so multiplying by
![]() $a(s_i)$
, we get
$a(s_i)$
, we get
![]() $a(s_i)Y = a(s_j)Y$
.
$a(s_i)Y = a(s_j)Y$
.
But then we have written X as a finite disjoint union of closed sets. Since X is connected, we must have
![]() $a(s_i)Y = X$
for every
$a(s_i)Y = X$
for every
![]() $i = 0, \dots, k-1$
. In particular,
$i = 0, \dots, k-1$
. In particular,
![]() $Y = X$
, so
$Y = X$
, so
![]() $(T^{rn})_{n \in \mathcal{O}_K}$
is ergodic.
$(T^{rn})_{n \in \mathcal{O}_K}$
is ergodic.
2·3. Weyl systems
The results in this paper depend critically on understanding polynomial orbits in Weyl systems. Following [
Reference Bergelson, Leibman and Lesigne10
], we call a topological dynamical system (X, T) a Weyl system if X is a compact abelian Lie group and T is a
![]() $\mathbb{Z}^d$
-action by unipotent affine tranformations. In proving our multiple recurrence results, we will focus our attention on connected Weyl systems, that is Weyl systems where X is connected (and hence a torus).
$\mathbb{Z}^d$
-action by unipotent affine tranformations. In proving our multiple recurrence results, we will focus our attention on connected Weyl systems, that is Weyl systems where X is connected (and hence a torus).
The main result on polynomial orbits is the following:
Proposition 2·5. (cf. [
Reference Bergelson, Leibman and Lesigne10
, proposition 3·2]). Let (X, T) be a
![]() $\mathbb{Z}^d$
-Weyl system and
$\mathbb{Z}^d$
-Weyl system and
![]() $p_1, \dots, p_m \;:\; \mathbb{Z}^d \to \mathbb{Z}^d$
polynomials. Then for every
$p_1, \dots, p_m \;:\; \mathbb{Z}^d \to \mathbb{Z}^d$
polynomials. Then for every
![]() $x \in X$
,
$x \in X$
,
![]() $Y \;:\!=\; \overline{\left\{ \left( T^{p_1(n)}x, \dots, T^{p_m(n)}x \right) \;:\; n \in \mathbb{Z}^d \right\}}$
is a union of finitely many subtori
$Y \;:\!=\; \overline{\left\{ \left( T^{p_1(n)}x, \dots, T^{p_m(n)}x \right) \;:\; n \in \mathbb{Z}^d \right\}}$
is a union of finitely many subtori
![]() $(Y_w)_{w \in W}$
of
$(Y_w)_{w \in W}$
of
![]() $X^m$
. Moreover, there is a homomorphism
$X^m$
. Moreover, there is a homomorphism
![]() $\omega \;:\; \mathbb{Z}^d \to W$
such that the sequence
$\omega \;:\; \mathbb{Z}^d \to W$
such that the sequence
![]() $\left( T^{p_1(n)}x, \dots, T^{p_m(n)}x \right)_{n \in \omega^{-1}(w)}$
is well-distributed in
$\left( T^{p_1(n)}x, \dots, T^{p_m(n)}x \right)_{n \in \omega^{-1}(w)}$
is well-distributed in
![]() $Y_w$
for each
$Y_w$
for each
![]() $w \in W$
.
$w \in W$
.
This can be seen via a multivariable version of Weyl’s theorem on polynomial equidistribution in tori (see the explanation of [ Reference Bergelson, Leibman and Lesigne10 , proposition 3·2]) or as a special case of a more general result due to Leibman:
Theorem 2·6. ([
Reference Leibman35
, theorem B*]). Let
![]() $X = G/\Gamma$
be a nilmanifold. Let
$X = G/\Gamma$
be a nilmanifold. Let
![]() $g \;:\; \mathbb{Z}^d \to G$
be a polynomial map, and let
$g \;:\; \mathbb{Z}^d \to G$
be a polynomial map, and let
![]() $x \in X$
. There is a connected closed subgroup
$x \in X$
. There is a connected closed subgroup
![]() $H \subseteq G$
, a homomorphism
$H \subseteq G$
, a homomorphism
![]() $\omega \;:\; \mathbb{Z}^d \to W$
onto a finite group W, and a set
$\omega \;:\; \mathbb{Z}^d \to W$
onto a finite group W, and a set
![]() $\{x_w \;:\; w \in W\} \subseteq X$
such that the sets
$\{x_w \;:\; w \in W\} \subseteq X$
such that the sets
![]() $Y_w \;:\!=\; Hx_w$
,
$Y_w \;:\!=\; Hx_w$
,
![]() $w \in W$
, are closed in X and
$w \in W$
, are closed in X and
![]() $\left( g(n)x \right)_{n \in \omega^{-1}(w)}$
is well-distributed in
$\left( g(n)x \right)_{n \in \omega^{-1}(w)}$
is well-distributed in
![]() $Y_w$
for every
$Y_w$
for every
![]() $w \in W$
.
$w \in W$
.
As a consequence, we can deduce a simple criterion for checking that a polynomial sequence is well-distributed in a torus. First we need some notation. For a sequence
![]() $u \;:\; \mathbb{Z}^d \to \mathbb{T}^m$
with polynomial coordinates
$u \;:\; \mathbb{Z}^d \to \mathbb{T}^m$
with polynomial coordinates
![]() $u(n) = \left( u_1(n), \dots, u_m(n) \right)$
, we write
$u(n) = \left( u_1(n), \dots, u_m(n) \right)$
, we write
Corollary 2·7.
Let
![]() $\alpha_1, \dots, \alpha_r$
be rationally independent irrational elements of
$\alpha_1, \dots, \alpha_r$
be rationally independent irrational elements of
![]() $\mathbb{T}$
. Let
$\mathbb{T}$
. Let
![]() $u_1, \dots, u_r \;:\; \mathbb{Z}^l \to \mathbb{Z}^m$
be polynomials with zero constant term. Then the sequence
$u_1, \dots, u_r \;:\; \mathbb{Z}^l \to \mathbb{Z}^m$
be polynomials with zero constant term. Then the sequence
is well-distributed in the subtorus
![]() $\text{span}(u_1) + \cdots + \text{span}(u_r) \pmod{1}$
of
$\text{span}(u_1) + \cdots + \text{span}(u_r) \pmod{1}$
of
![]() $\mathbb{T}^m$
.
$\mathbb{T}^m$
.
Proof. The case
![]() $d = 1$
is handled by [
Reference Bergelson, Leibman and Lesigne10
, corollary 3·3]. The same proof works for general
$d = 1$
is handled by [
Reference Bergelson, Leibman and Lesigne10
, corollary 3·3]. The same proof works for general
![]() $d \in \mathbb{N}$
.
$d \in \mathbb{N}$
.
2·4. Properties of polynomials
Definition 2·8. The polynomials
![]() $p_1, \dots, p_m \in \mathbb{Q}[x_1, \dots, x_d]$
are algebraically independent (over
$p_1, \dots, p_m \in \mathbb{Q}[x_1, \dots, x_d]$
are algebraically independent (over
![]() $\mathbb{Q}$
) if, for every nonzero
$\mathbb{Q}$
) if, for every nonzero
![]() $f \in \mathbb{Q}[x_1, \dots, x_m]$
, the polynomial
$f \in \mathbb{Q}[x_1, \dots, x_m]$
, the polynomial
![]() $f(p_1, \dots, p_m)$
is nonzero.
$f(p_1, \dots, p_m)$
is nonzero.
Proposition 2·9.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $p(x) \in K[x]$
be a nonconstant
$p(x) \in K[x]$
be a nonconstant
![]() $\mathcal{O}_K$
-valued polynomial. Fix an integral basis
$\mathcal{O}_K$
-valued polynomial. Fix an integral basis
![]() $\{b_1, \dots, b_d\} \subseteq \mathcal{O}_K$
, and let
$\{b_1, \dots, b_d\} \subseteq \mathcal{O}_K$
, and let
![]() $p_1, \dots, p_d \in \mathbb{Q}[x_1, \dots, x_d]$
be
$p_1, \dots, p_d \in \mathbb{Q}[x_1, \dots, x_d]$
be
![]() $\mathbb{Z}$
-valued polynomials so that
$\mathbb{Z}$
-valued polynomials so that
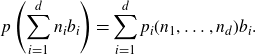 \begin{align*} p \left( \sum_{i=1}^d{n_ib_i} \right) = \sum_{i=1}^d{p_i(n_1, \dots, n_d)b_i}. \end{align*}
\begin{align*} p \left( \sum_{i=1}^d{n_ib_i} \right) = \sum_{i=1}^d{p_i(n_1, \dots, n_d)b_i}. \end{align*}
Then the polynomials
![]() $p_1, \dots, p_d$
are algebraically independent (over
$p_1, \dots, p_d$
are algebraically independent (over
![]() $\mathbb{Q}$
).
$\mathbb{Q}$
).
Proof. By [ Reference Lefschetz34 , chapter I, 11·4], it suffices to check that the Jacobian matrix
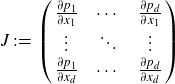 \begin{align*} J \;:\!=\; \left( \begin{array}{c@{\quad}c@{\quad}c} \frac{\partial p_1}{\partial x_1} & \cdots & \frac{\partial p_d}{\partial x_1} \\ \vdots & \ddots & \vdots \\ \frac{\partial p_1}{\partial x_d} & \cdots & \frac{\partial p_d}{\partial x_d} \end{array} \right) \end{align*}
\begin{align*} J \;:\!=\; \left( \begin{array}{c@{\quad}c@{\quad}c} \frac{\partial p_1}{\partial x_1} & \cdots & \frac{\partial p_d}{\partial x_1} \\ \vdots & \ddots & \vdots \\ \frac{\partial p_1}{\partial x_d} & \cdots & \frac{\partial p_d}{\partial x_d} \end{array} \right) \end{align*}
has full rank.
But the ith row of the Jacobian matrix is given by
Since p is nonconstant,
![]() $p'(x) \not\equiv 0$
. Moreover,
$p'(x) \not\equiv 0$
. Moreover,
![]() $\{b_1, \dots, b_d\}$
is linearly independent over
$\{b_1, \dots, b_d\}$
is linearly independent over
![]() $\mathbb{Q}$
, so the rows of J are linearly independent. Therefore, J has full rank, so
$\mathbb{Q}$
, so the rows of J are linearly independent. Therefore, J has full rank, so
![]() $p_1, \dots p_d$
are algebraically independent.
$p_1, \dots p_d$
are algebraically independent.
Proposition 2·10.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
, and let
$\mathcal{O}_K$
, and let
![]() $\{b_1, \dots, b_d\}$
be an integral basis in
$\{b_1, \dots, b_d\}$
be an integral basis in
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\{p_1, \dots, p_k\} \subseteq K[x]$
be an independent family of polynomials (over K). For each
$\{p_1, \dots, p_k\} \subseteq K[x]$
be an independent family of polynomials (over K). For each
![]() $i = 1, \dots, k$
, let
$i = 1, \dots, k$
, let
![]() $p_{i,1}, \dots, p_{i,d} \in \mathbb{Q}[x_1, \dots, x_d]$
be the coordinate polynomials so that
$p_{i,1}, \dots, p_{i,d} \in \mathbb{Q}[x_1, \dots, x_d]$
be the coordinate polynomials so that
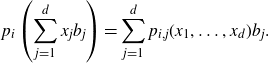 \begin{align*} p_i \left( \sum_{j=1}^d{x_jb_j} \right) = \sum_{j=1}^d{p_{i,j}(x_1, \dots, x_d)b_j}. \end{align*}
\begin{align*} p_i \left( \sum_{j=1}^d{x_jb_j} \right) = \sum_{j=1}^d{p_{i,j}(x_1, \dots, x_d)b_j}. \end{align*}
Then the family
![]() $\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\} \subseteq \mathbb{Q}[x_1, \dots, x_d]$
is independent (over
$\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\} \subseteq \mathbb{Q}[x_1, \dots, x_d]$
is independent (over
![]() $\mathbb{Q}$
). That is, for any
$\mathbb{Q}$
). That is, for any
![]() $(c_{i,j})_{1 \le i \le k, 1 \le j \le d} \in \mathbb{Q}^{kd} \setminus \{0\}$
, the polynomial
$(c_{i,j})_{1 \le i \le k, 1 \le j \le d} \in \mathbb{Q}^{kd} \setminus \{0\}$
, the polynomial
![]() $\sum_{i=1}^k{\sum_{j=1}^d{c_{i,j}p_{i,j}}}$
is nonconstant.
$\sum_{i=1}^k{\sum_{j=1}^d{c_{i,j}p_{i,j}}}$
is nonconstant.
Proof. First, since
![]() $\{b_1, \dots, b_d\}$
is linearly independent over
$\{b_1, \dots, b_d\}$
is linearly independent over
![]() $\mathbb{Q}$
, the family
$\mathbb{Q}$
, the family
![]() $\{b_jp_i \;:\; 1 \le i \le k, 1 \le j \le d\} \subseteq K[x]$
is independent over
$\{b_jp_i \;:\; 1 \le i \le k, 1 \le j \le d\} \subseteq K[x]$
is independent over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Now let
![]() $q_{i,j} \in \mathbb{Q}[x_1, \dots, x_d]$
be the
$q_{i,j} \in \mathbb{Q}[x_1, \dots, x_d]$
be the
![]() $b_1$
-coordinate of
$b_1$
-coordinate of
![]() $b_jp_i$
. That is,
$b_jp_i$
. That is,
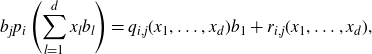 \begin{align*} b_jp_i \left( \sum_{l=1}^d{x_lb_l} \right) = q_{i,j}(x_1, \dots, x_d)b_1 + r_{i,j}(x_1, \dots, x_d), \end{align*}
\begin{align*} b_jp_i \left( \sum_{l=1}^d{x_lb_l} \right) = q_{i,j}(x_1, \dots, x_d)b_1 + r_{i,j}(x_1, \dots, x_d), \end{align*}
where
![]() $r_{i,j}(x_1, \dots, x_d) \in \text{span}_{\mathbb{Q}}\{b_2, \dots, b_d\}$
. We claim that
$r_{i,j}(x_1, \dots, x_d) \in \text{span}_{\mathbb{Q}}\{b_2, \dots, b_d\}$
. We claim that
![]() $\{q_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\}$
is independent over
$\{q_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\}$
is independent over
![]() $\mathbb{Q}$
. Suppose not. Then for some
$\mathbb{Q}$
. Suppose not. Then for some
![]() $(c_{i,j})_{1 \le i \le k, 1 \le j \le d} \in \mathbb{Q}^{kd} \setminus \{0\}$
and some
$(c_{i,j})_{1 \le i \le k, 1 \le j \le d} \in \mathbb{Q}^{kd} \setminus \{0\}$
and some
![]() $c \in \mathbb{Q}$
, we have
$c \in \mathbb{Q}$
, we have
 \begin{align*} \sum_{i=1}^k{\sum_{j=1}^d{c_{i,j}q_{i,j}(x_1, \dots, x_d)}} = c. \end{align*}
\begin{align*} \sum_{i=1}^k{\sum_{j=1}^d{c_{i,j}q_{i,j}(x_1, \dots, x_d)}} = c. \end{align*}
Then
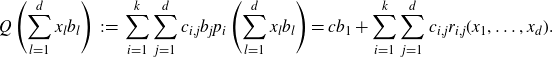 \begin{align*} Q \left( \sum_{l=1}^d{x_lb_l} \right) \;:\!=\; \sum_{i=1}^k{\sum_{j=1}^d{c_{i,j}b_jp_i \left( \sum_{l=1}^d{x_lb_l} \right)}} = cb_1 + \sum_{i=1}^k{\sum_{j=1}^d{c_{i,j}r_{i,j}(x_1, \dots, x_d)}}. \end{align*}
\begin{align*} Q \left( \sum_{l=1}^d{x_lb_l} \right) \;:\!=\; \sum_{i=1}^k{\sum_{j=1}^d{c_{i,j}b_jp_i \left( \sum_{l=1}^d{x_lb_l} \right)}} = cb_1 + \sum_{i=1}^k{\sum_{j=1}^d{c_{i,j}r_{i,j}(x_1, \dots, x_d)}}. \end{align*}
Hence, for the polynomial function
![]() $f \left( \sum_{l=1}^d{x_lb_l} \right) \;:\!=\; x_1 - c$
, we have
$f \left( \sum_{l=1}^d{x_lb_l} \right) \;:\!=\; x_1 - c$
, we have
![]() $f(Q) = 0$
. By Proposition 2·9, it follows that Q is constant. But
$f(Q) = 0$
. By Proposition 2·9, it follows that Q is constant. But
![]() $\{b_jp_i \;:\; 1 \le i \le k, 1 \le j \le d\}$
is independent over
$\{b_jp_i \;:\; 1 \le i \le k, 1 \le j \le d\}$
is independent over
![]() $\mathbb{Q}$
, so this is a contradiction.
$\mathbb{Q}$
, so this is a contradiction.
For
![]() $1 \le j, l, m \le d$
, let
$1 \le j, l, m \le d$
, let
![]() $a_{j,l,m} \in \mathbb{Z}$
so that
$a_{j,l,m} \in \mathbb{Z}$
so that
![]() $b_jb_l = \sum_{m=1}^d{a_{j,l,m}b_m}$
. By direct computation, we have
$b_jb_l = \sum_{m=1}^d{a_{j,l,m}b_m}$
. By direct computation, we have
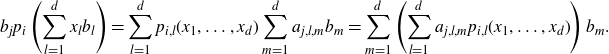 \begin{align*} b_jp_i \left( \sum_{l=1}^d{x_lb_l} \right) = \sum_{l=1}^d{p_{i,l}(x_1, \dots, x_d) \sum_{m=1}^d{a_{j,l,m}b_m}} = \sum_{m=1}^d{ \left( \sum_{l=1}^d{a_{j,l,m}p_{i,l}(x_1, \dots, x_d)} \right) b_m}. \end{align*}
\begin{align*} b_jp_i \left( \sum_{l=1}^d{x_lb_l} \right) = \sum_{l=1}^d{p_{i,l}(x_1, \dots, x_d) \sum_{m=1}^d{a_{j,l,m}b_m}} = \sum_{m=1}^d{ \left( \sum_{l=1}^d{a_{j,l,m}p_{i,l}(x_1, \dots, x_d)} \right) b_m}. \end{align*}
Thus,
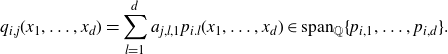 \begin{align*} q_{i,j}(x_1, \dots, x_d) = \sum_{l=1}^d{a_{j,l,1}p_{i.l}(x_1, \dots, x_d)} \in \text{span}_{\mathbb{Q}}{\{p_{i,1}, \dots, p_{i,d}\}}. \end{align*}
\begin{align*} q_{i,j}(x_1, \dots, x_d) = \sum_{l=1}^d{a_{j,l,1}p_{i.l}(x_1, \dots, x_d)} \in \text{span}_{\mathbb{Q}}{\{p_{i,1}, \dots, p_{i,d}\}}. \end{align*}
Therefore,
![]() $\text{span}{\left( \{1\} \cup \{q_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\} \right)} \subseteq \text{span}{\left( \{1\} \cup \{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\} \right)}$
. It follows that
$\text{span}{\left( \{1\} \cup \{q_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\} \right)} \subseteq \text{span}{\left( \{1\} \cup \{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\} \right)}$
. It follows that
![]() $\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\}$
is independent over
$\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le d\}$
is independent over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Lemma 2·11.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\{p_1, \dots, p_k\} \subseteq K[x]$
be jointly intersective
$\{p_1, \dots, p_k\} \subseteq K[x]$
be jointly intersective
![]() $\mathcal{O}_K$
-valued polynomials. Let
$\mathcal{O}_K$
-valued polynomials. Let
![]() $r \in \mathcal{O}_K \setminus \{0\}$
. Then there exists
$r \in \mathcal{O}_K \setminus \{0\}$
. Then there exists
![]() $\xi \in \mathcal{O}_K$
and
$\xi \in \mathcal{O}_K$
and
![]() $D \in \mathcal{O}_K \setminus \{0\}$
such that
$D \in \mathcal{O}_K \setminus \{0\}$
such that
for
![]() $i = 1, \dots, k$
.
$i = 1, \dots, k$
.
Proof. The subgroup
![]() $r\mathcal{O}_K$
has finite index in
$r\mathcal{O}_K$
has finite index in
![]() $\mathcal{O}_K$
, so there exists
$\mathcal{O}_K$
, so there exists
![]() $\xi \in \mathcal{O}_K$
such that
$\xi \in \mathcal{O}_K$
such that
![]() $p_i(\xi) \in r\mathcal{O}_K$
for
$p_i(\xi) \in r\mathcal{O}_K$
for
![]() $i = 1, \dots, k$
.
$i = 1, \dots, k$
.
Fix
![]() $1 \le i \le k$
. Now write
$1 \le i \le k$
. Now write
![]() $p_i(x) = a_m x^m + \cdots + a_1 x + a_0$
with
$p_i(x) = a_m x^m + \cdots + a_1 x + a_0$
with
![]() $a_0, a_1, \dots, a_m \in K$
. Since
$a_0, a_1, \dots, a_m \in K$
. Since
![]() $p_i$
is
$p_i$
is
![]() $\mathcal{O}_K$
-valued, we have
$\mathcal{O}_K$
-valued, we have
![]() $a_0 = p_i(0) \in \mathcal{O}_K$
. Let
$a_0 = p_i(0) \in \mathcal{O}_K$
. Let
![]() $D_i \in \mathcal{O}_K$
so that
$D_i \in \mathcal{O}_K$
so that
![]() $D_ia_j \in \mathcal{O}_K$
for all
$D_ia_j \in \mathcal{O}_K$
for all
![]() $j = 1, \dots, m$
. We claim
$j = 1, \dots, m$
. We claim
![]() $p_i(\xi + D_ir\mathcal{O}_K) \subseteq r\mathcal{O}_K$
. Indeed, for
$p_i(\xi + D_ir\mathcal{O}_K) \subseteq r\mathcal{O}_K$
. Indeed, for
![]() $n \in \mathcal{O}_K$
, we have
$n \in \mathcal{O}_K$
, we have
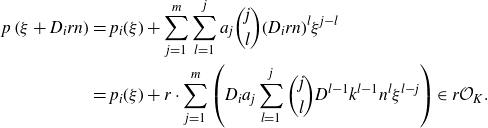 \begin{align*} p \left( \xi + D_irn \right) & = p_i(\xi) + \sum_{j=1}^m{\sum_{l=1}^j{a_j\binom{j}{l}(D_irn)^l\xi^{j-l}}} \\ & = p_i(\xi) + r \cdot \sum_{j=1}^m{\left( D_ia_j \sum_{l=1}^j{\binom{j}{l}D^{l-1}k^{l-1}n^l \xi^{l-j}} \right)} \in r \mathcal{O}_K. \end{align*}
\begin{align*} p \left( \xi + D_irn \right) & = p_i(\xi) + \sum_{j=1}^m{\sum_{l=1}^j{a_j\binom{j}{l}(D_irn)^l\xi^{j-l}}} \\ & = p_i(\xi) + r \cdot \sum_{j=1}^m{\left( D_ia_j \sum_{l=1}^j{\binom{j}{l}D^{l-1}k^{l-1}n^l \xi^{l-j}} \right)} \in r \mathcal{O}_K. \end{align*}
Taking
![]() $D = r \cdot \text{lcm}(D_1, \dots, D_k)$
completes the proof.
$D = r \cdot \text{lcm}(D_1, \dots, D_k)$
completes the proof.
2·5. Eligible collections
Theorem C and Theorem D each establish characteristic factors for certain polynomial configurations in ergodic systems. In both cases, it is significantly easier to deal with totally ergodic systems. The notion of eligible collections, introduced by Frantzikinakis in [
Reference Frantzikinakis19
] for
![]() $\mathbb{Z}$
-valued polynomials, can be utilized to reduce the ergodic case to the simpler case in which the system is totally ergodic.
$\mathbb{Z}$
-valued polynomials, can be utilized to reduce the ergodic case to the simpler case in which the system is totally ergodic.
Definition 2·12. Let
![]() $\mathcal{P}$
be a collection of families of k
$\mathcal{P}$
be a collection of families of k
![]() $\mathcal{O}_K$
-valued polynomials. We say that
$\mathcal{O}_K$
-valued polynomials. We say that
![]() $\mathcal{P}$
is eligible if for any
$\mathcal{P}$
is eligible if for any
![]() $\{p_1, \dots, p_k\} \in \mathcal{P}$
, we have:
$\{p_1, \dots, p_k\} \in \mathcal{P}$
, we have:
-
(i)
 $\{p_1(n) - p_1(0), \dots, p_k(n) - p_k(0)\} \in \mathcal{P}$
;
$\{p_1(n) - p_1(0), \dots, p_k(n) - p_k(0)\} \in \mathcal{P}$
; -
(ii)
 $\{p_1(rn+s), \dots, p_k(rn+s)\} \in \mathcal{P}$
for any
$\{p_1(rn+s), \dots, p_k(rn+s)\} \in \mathcal{P}$
for any
 $r, s \in \mathcal{O}_K$
with
$r, s \in \mathcal{O}_K$
with
 $r \ne 0$
;
$r \ne 0$
; -
(iii)
 $\{cp_1(n), \dots, cp_k(n)\} \in \mathcal{P}$
for any
$\{cp_1(n), \dots, cp_k(n)\} \in \mathcal{P}$
for any
 $c \in K \setminus \{0\}$
such that
$c \in K \setminus \{0\}$
such that
 $cp_i$
is
$cp_i$
is
 $\mathcal{O}_K$
-valued for
$\mathcal{O}_K$
-valued for
 $i = 1, \dots, k$
.
$i = 1, \dots, k$
.
Proposition 2·13 (cf. [
Reference Frantzikinakis19
, proposition 4·1]). Let
![]() $\mathcal{P}$
be eligible. Suppose that for some
$\mathcal{P}$
be eligible. Suppose that for some
![]() $m \in \mathbb{N}$
, the nilfactor
$m \in \mathbb{N}$
, the nilfactor
![]() $\mathcal{Z}_m$
is characteristic for every
$\mathcal{Z}_m$
is characteristic for every
![]() $P \in \mathcal{P}$
in totally ergodic systems. Then
$P \in \mathcal{P}$
in totally ergodic systems. Then
![]() $\mathcal{Z}_m$
is characteristic for every
$\mathcal{Z}_m$
is characteristic for every
![]() $P \in \mathcal{P}$
in ergodic systems.
$P \in \mathcal{P}$
in ergodic systems.
Proof. Let
![]() $(X, \mathcal{B}, \mu, T)$
be an ergodic
$(X, \mathcal{B}, \mu, T)$
be an ergodic
![]() $\mathcal{O}_K$
-system. Let
$\mathcal{O}_K$
-system. Let
![]() $f_1, \dots, f_k \in L^{\infty}(\mu)$
, and suppose
$f_1, \dots, f_k \in L^{\infty}(\mu)$
, and suppose
![]() $\mathbb{E}\left[ {f_i} \mid {\mathcal{Z}_m} \right] = 0$
for some
$\mathbb{E}\left[ {f_i} \mid {\mathcal{Z}_m} \right] = 0$
for some
![]() $i = 1, \dots, k$
. Without loss of generality,
$i = 1, \dots, k$
. Without loss of generality,
![]() $i = 1$
. We want to show
$i = 1$
. We want to show
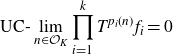 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{p_i(n)}f_i} } = 0 \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{p_i(n)}f_i} } = 0 \end{align*}
in
![]() $L^2(\mu)$
. Shifting by the constant terms and using property (i), we may assume
$L^2(\mu)$
. Shifting by the constant terms and using property (i), we may assume
![]() $p_i(0) = 0$
.
$p_i(0) = 0$
.
By Theorem 1·13, we may assume that
![]() $X = G/\Gamma$
is a nilmanifold and T acts by niltranslations
$X = G/\Gamma$
is a nilmanifold and T acts by niltranslations
![]() $T^nx = a(n)x$
with
$T^nx = a(n)x$
with
![]() $a(n) \in G$
. We claim that there exists
$a(n) \in G$
. We claim that there exists
![]() $r \in \mathcal{O}_K$
such that the (finitely many) ergodic components of the action
$r \in \mathcal{O}_K$
such that the (finitely many) ergodic components of the action
![]() $\left( T^{rn} \right)_{n \in \mathcal{O}_K}$
are totally ergodic. Let
$\left( T^{rn} \right)_{n \in \mathcal{O}_K}$
are totally ergodic. Let
![]() $\mathcal{Z}$
be the Kronecker factor of (X, T). This is an action by rotations on an abelian Lie group of the form
$\mathcal{Z}$
be the Kronecker factor of (X, T). This is an action by rotations on an abelian Lie group of the form
![]() $\mathbb{Z}_{a_1} \times \cdots \times \mathbb{Z}_{a_d} \times \mathbb{T}^{c}$
with
$\mathbb{Z}_{a_1} \times \cdots \times \mathbb{Z}_{a_d} \times \mathbb{T}^{c}$
with
![]() $a_1, \dots, a_d \in \mathbb{N}, c \in \mathbb{N} \cup \{0\}$
. Set
$a_1, \dots, a_d \in \mathbb{N}, c \in \mathbb{N} \cup \{0\}$
. Set
![]() $a \;:\!=\; \prod_{j=1}^d{a_j} \in \mathbb{N}$
. Letting
$a \;:\!=\; \prod_{j=1}^d{a_j} \in \mathbb{N}$
. Letting
![]() $r = a(b_1 + \cdots + b_d)$
, where
$r = a(b_1 + \cdots + b_d)$
, where
![]() $\{b_1, \dots, b_d\}$
is an integral basis for
$\{b_1, \dots, b_d\}$
is an integral basis for
![]() $\mathcal{O}_K$
, we then have that the ergodic components of
$\mathcal{O}_K$
, we then have that the ergodic components of
![]() $\left( T^{rn} \right)_{n \in \mathcal{O}_K}$
are totally ergodic (we have trivialized the rational component of the Kronecker factor).
$\left( T^{rn} \right)_{n \in \mathcal{O}_K}$
are totally ergodic (we have trivialized the rational component of the Kronecker factor).
Since
![]() $p_i(0) = 0$
for each
$p_i(0) = 0$
for each
![]() $i = 1, \dots, k$
, there exist
$i = 1, \dots, k$
, there exist
![]() $D \in \mathcal{O}_K \setminus \{0\}$
so that the polynomials
$D \in \mathcal{O}_K \setminus \{0\}$
so that the polynomials
![]() $q_i(n) \;:\!=\; r^{-1}p_i(Dn)$
are
$q_i(n) \;:\!=\; r^{-1}p_i(Dn)$
are
![]() $\mathcal{O}_K$
-valued by Lemma 2·11. By properties (ii) and (iii),
$\mathcal{O}_K$
-valued by Lemma 2·11. By properties (ii) and (iii),
![]() $\{q_1, \dots, q_k\} \in \mathcal{P}$
.
$\{q_1, \dots, q_k\} \in \mathcal{P}$
.
Now,
![]() $\left( T^{rn} \right)_{n \in \mathcal{O}_K}$
has finitely many ergodic components and
$\left( T^{rn} \right)_{n \in \mathcal{O}_K}$
has finitely many ergodic components and
![]() $\mathcal{Z}_m(T^{rn}) \subseteq \mathcal{Z}_m(T^n)$
, so
$\mathcal{Z}_m(T^{rn}) \subseteq \mathcal{Z}_m(T^n)$
, so
![]() $\mathbb{E}\left[ {f_1} \mid {\mathcal{Z}^{(j)}_m} \right] = 0$
, where
$\mathbb{E}\left[ {f_1} \mid {\mathcal{Z}^{(j)}_m} \right] = 0$
, where
![]() $\mathcal{Z}^{(j)}_m$
is the nilfactor for the jth ergodic component of
$\mathcal{Z}^{(j)}_m$
is the nilfactor for the jth ergodic component of
![]() $T^{rn}$
. Summing over the finitely many ergodic components of
$T^{rn}$
. Summing over the finitely many ergodic components of
![]() $T^{rn}$
, we thus have
$T^{rn}$
, we thus have
 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{p_i(Dn)}f_i} } = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{r \cdot q_i(n)}f_i} } = 0. \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{p_i(Dn)}f_i} } = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{r \cdot q_i(n)}f_i} } = 0. \end{align*}
Note that by the proof of Lemma 2·11,
![]() $p_i(Dn + s) \equiv p_i(s) \pmod{r\mathcal{O}_K}$
. Hence,
$p_i(Dn + s) \equiv p_i(s) \pmod{r\mathcal{O}_K}$
. Hence,
![]() $q^{(s)}_i(n) \;:\!=\; r^{-1}(p_i(Dn+s) - p_i(s))$
is
$q^{(s)}_i(n) \;:\!=\; r^{-1}(p_i(Dn+s) - p_i(s))$
is
![]() $\mathcal{O}_K$
-valued. Moreover, since
$\mathcal{O}_K$
-valued. Moreover, since
![]() $\mathcal{P}$
is eligible, we have
$\mathcal{P}$
is eligible, we have
![]() $\left\{ q^{(s)}_1, \dots, q^{(s)}_k \right\} \in \mathcal{P}$
. By assumption,
$\left\{ q^{(s)}_1, \dots, q^{(s)}_k \right\} \in \mathcal{P}$
. By assumption,
![]() $\mathbb{E}\left[ {f_i} \mid {\mathcal{Z}_m} \right] = 0$
for some
$\mathbb{E}\left[ {f_i} \mid {\mathcal{Z}_m} \right] = 0$
for some
![]() $i = 1, \dots, k$
. It follows that
$i = 1, \dots, k$
. It follows that
![]() $\mathbb{E}\left[ {T^{p_i(s)}f_i} \mid {\mathcal{Z}_m} \right] = 0$
, since
$\mathbb{E}\left[ {T^{p_i(s)}f_i} \mid {\mathcal{Z}_m} \right] = 0$
, since
![]() $\mathcal{Z}_m$
is T-invariant. Thus, by the argument in the previous paragraph, we have
$\mathcal{Z}_m$
is T-invariant. Thus, by the argument in the previous paragraph, we have
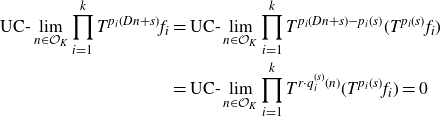 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{p_i(Dn+s)}f_i} } & = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{p_i(Dn+s)-p_i(s)}(T^{p_i(s)}f_i)} } \\ & = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{r \cdot q^{(s)}_i(n)}(T^{p_i(s)}f_i)} } = 0 \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{p_i(Dn+s)}f_i} } & = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{p_i(Dn+s)-p_i(s)}(T^{p_i(s)}f_i)} } \\ & = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{r \cdot q^{(s)}_i(n)}(T^{p_i(s)}f_i)} } = 0 \end{align*}
for
![]() $s \in \mathcal{O}_K/r\mathcal{O}_K$
. This completes the proof.
$s \in \mathcal{O}_K/r\mathcal{O}_K$
. This completes the proof.
3. Characteristic factors
3·1. Proof of Theorem C
We want to prove that the rational Kronecker factor,
![]() $\mathcal{K}_{rat}$
, is characteristic for the average
$\mathcal{K}_{rat}$
, is characteristic for the average
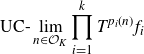 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}}\end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}}\end{align*}
when
![]() $p_1, \dots, p_k \in K[x]$
are independent
$p_1, \dots, p_k \in K[x]$
are independent
![]() $\mathcal{O}_K$
-valued polynomials.
$\mathcal{O}_K$
-valued polynomials.
We will first prove a special case:
Theorem 3·1.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Suppose
$\mathcal{O}_K$
. Suppose
![]() $p_1, \dots, p_k \in K[x]$
are independent
$p_1, \dots, p_k \in K[x]$
are independent
![]() $\mathcal{O}_K$
-valued polynomials. If
$\mathcal{O}_K$
-valued polynomials. If
![]() $\left( X, \mathcal{B}, \mu, T \right)$
is a totally ergodic
$\left( X, \mathcal{B}, \mu, T \right)$
is a totally ergodic
![]() $\mathcal{O}_K$
-system and
$\mathcal{O}_K$
-system and
![]() $f_1, \dots, f_k \in L^{\infty}(\mu)$
, then
$f_1, \dots, f_k \in L^{\infty}(\mu)$
, then
 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = \prod_{i=1}^k{\int_X{f_i\;d\mu}}. \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = \prod_{i=1}^k{\int_X{f_i\;d\mu}}. \end{align*}
Remark 3·2. After a previous version of this paper appeared on arXiv, Best and Ferré Moragues reproved Theorem 3·1 using a different method (see [ Reference Best and Ferré Moragues17 , thoerem 1·6]).
3·1·1. Reduction to Weyl systems
Recall that a sequence
![]() $(x_n)_{n \in \mathcal{O}_K}$
in a compact topological space X is well-distributed with respect to a probability measure
$(x_n)_{n \in \mathcal{O}_K}$
in a compact topological space X is well-distributed with respect to a probability measure
![]() $\mu$
on X if
$\mu$
on X if
![]() $\text{UC-}\lim_{n \in \mathcal{O}_K}{\delta_{x_n}} = \mu$
in the weak-* topology. That is, for any continuous function
$\text{UC-}\lim_{n \in \mathcal{O}_K}{\delta_{x_n}} = \mu$
in the weak-* topology. That is, for any continuous function
![]() $f \;:\; X \to \mathbb{C}$
and any Følner sequence
$f \;:\; X \to \mathbb{C}$
and any Følner sequence
![]() $(\Phi_N)_{N \in \mathbb{N}}$
in
$(\Phi_N)_{N \in \mathbb{N}}$
in
![]() $(\mathcal{O}_K, +)$
, one has
$(\mathcal{O}_K, +)$
, one has
By Theorem 1·13, Theorem 3·1 is equivalent to the following equidistribution result:
Theorem 3·3.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $(X, \mathcal{B}, \mu, T)$
be a totally ergodic
$(X, \mathcal{B}, \mu, T)$
be a totally ergodic
![]() $\mathcal{O}_K$
-nilsystem. Let
$\mathcal{O}_K$
-nilsystem. Let
![]() $\{p_1, \dots, p_k\} \subseteq K[x]$
be independent
$\{p_1, \dots, p_k\} \subseteq K[x]$
be independent
![]() $\mathcal{O}_K$
-valued polynomials. Then for almost every
$\mathcal{O}_K$
-valued polynomials. Then for almost every
![]() $x \in X$
, the sequence
$x \in X$
, the sequence
![]() $\left( T^{p_1(n)}x, \dots, T^{p_k(n)}x \right)_{n \in \mathcal{O}_K}$
is well-distributed in
$\left( T^{p_1(n)}x, \dots, T^{p_k(n)}x \right)_{n \in \mathcal{O}_K}$
is well-distributed in
![]() $X^k$
.
$X^k$
.
Having reduced to an equidistribution result on nilmanifolds, we can now make several more reductions. First, by Proposition 2·4, the nilmanifold in Theorem 3·3 is necessarily connected, since it admits a totally ergodic action by niltranslations. Next, by Proposition 2·10, we may expand the polynomials
![]() $p_1, \dots, p_k$
in coordinates with respect to an integral basis in order to obtain an independent family of
$p_1, \dots, p_k$
in coordinates with respect to an integral basis in order to obtain an independent family of
![]() $\mathbb{Z}$
-valued polynomials. Hence, Theorem 3·3 follows from:
$\mathbb{Z}$
-valued polynomials. Hence, Theorem 3·3 follows from:
Theorem 3·4.
Let
![]() $d, k, l \in \mathbb{N}$
. Let
$d, k, l \in \mathbb{N}$
. Let
![]() $\left( X, \mathcal{B}, \mu, T \right)$
be an ergodic, connected
$\left( X, \mathcal{B}, \mu, T \right)$
be an ergodic, connected
![]() $\mathbb{Z}^l$
-nilsystem. Let
$\mathbb{Z}^l$
-nilsystem. Let
![]() $\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le l\} \subseteq \mathbb{Q}[x_1, \dots, x_d]$
be a family of independent
$\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le l\} \subseteq \mathbb{Q}[x_1, \dots, x_d]$
be a family of independent
![]() $\mathbb{Z}$
-valued polynomials. Then the sequence
$\mathbb{Z}$
-valued polynomials. Then the sequence
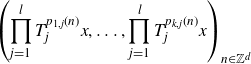 \begin{align*} \left( \prod_{j=1}^l{T_j^{p_{1,j}(n)}}x, \dots, \prod_{j=1}^l{T_j^{p_{k,j}(n)}}x \right)_{n \in \mathbb{Z}^d} \end{align*}
\begin{align*} \left( \prod_{j=1}^l{T_j^{p_{1,j}(n)}}x, \dots, \prod_{j=1}^l{T_j^{p_{k,j}(n)}}x \right)_{n \in \mathbb{Z}^d} \end{align*}
is well-distributed in
![]() $X^k$
for every x in a co-meager set of full measure.
$X^k$
for every x in a co-meager set of full measure.
Now we will reduce from a connected nilystem to the case that (X, T) is a Weyl system, i.e. X is a finite-dimensional torus and T acts by unipotent affine transformations. Let
![]() $G_0$
be the connected component of the identity in G,
$G_0$
be the connected component of the identity in G,
![]() $Z = X/[G_0, G_0]$
, and
$Z = X/[G_0, G_0]$
, and
![]() $\pi \;:\; G \to Z$
the projection map. The following result of Leibman shows that we can reduce to studying orbits in Z:
$\pi \;:\; G \to Z$
the projection map. The following result of Leibman shows that we can reduce to studying orbits in Z:
Theorem 3·5 ([
Reference Leibman35
, theorem C]). Let
![]() $X = G/\Gamma$
be a connected nilmanifold,
$X = G/\Gamma$
be a connected nilmanifold,
![]() $x \in X$
, and
$x \in X$
, and
![]() $g \;:\; \mathbb{Z}^d \to G$
a polynomial map. The following are equivalent:
$g \;:\; \mathbb{Z}^d \to G$
a polynomial map. The following are equivalent:
-
(i) the orbit
 $\left\{ g(n)x \;:\; n \in \mathbb{Z}^d \right\}$
is dense in X;
$\left\{ g(n)x \;:\; n \in \mathbb{Z}^d \right\}$
is dense in X; -
(ii)
 $\left\{ g(n)\pi(x) \;:\; n \in \mathbb{Z}^d \right\}$
is dense in Z;
$\left\{ g(n)\pi(x) \;:\; n \in \mathbb{Z}^d \right\}$
is dense in Z; -
(iii)
 $\left( g(n)x \right)_{n \in \mathbb{Z}^d}$
is well-distributed in X;
$\left( g(n)x \right)_{n \in \mathbb{Z}^d}$
is well-distributed in X; -
(iv)
 $\left( g(n)\pi(x) \right)_{n \in \mathbb{Z}^d}$
is well-distributed in Z.
$\left( g(n)\pi(x) \right)_{n \in \mathbb{Z}^d}$
is well-distributed in Z.
Lemma 3·6 (cf. [
Reference Frantzikinakis and Kra20
, proposition 2·1]). Without loss of generality,
![]() $G_0$
is abelian.
$G_0$
is abelian.
Proof. Use Theorem 3·5 to reduce to the projection onto Z. Now,
![]() $(G/[G_0, G_0])_0$
is an abelian group, and a factor of a totally ergodic system is totally ergodic.
$(G/[G_0, G_0])_0$
is an abelian group, and a factor of a totally ergodic system is totally ergodic.
Lemma 3·7 (cf. [ Reference Frantzikinakis and Kra20 , propositions 3·1 and 3·2]). Without loss of generality, (X,T) is a connected Weyl system.
Proof. To reduce from a connected nilsystem such that
![]() $G_0$
is abelian to a connected Weyl system, see [
Reference Frantzikinakis and Kra20
, proposition 3·1]. The isomorphism between a niltranslation and a unipotent affine transformation does not depend on the element of G defining the niltranslation, so the result still holds for d commuting niltranslations.
$G_0$
is abelian to a connected Weyl system, see [
Reference Frantzikinakis and Kra20
, proposition 3·1]. The isomorphism between a niltranslation and a unipotent affine transformation does not depend on the element of G defining the niltranslation, so the result still holds for d commuting niltranslations.
We have therefore reduced Theorem 3·1 to the following result about well-distribution of polynomial orbits for unipotent affine actions on tori:
Theorem 3·8.
Let
![]() $d, l, k, m \in \mathbb{N}$
. Let
$d, l, k, m \in \mathbb{N}$
. Let
![]() $\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le l\} \subseteq \mathbb{Q}[x_1, \dots, x_d]$
be
$\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le l\} \subseteq \mathbb{Q}[x_1, \dots, x_d]$
be
![]() $\mathbb{Z}$
-valued and independent over
$\mathbb{Z}$
-valued and independent over
![]() $\mathbb{Q}$
. Let
$\mathbb{Q}$
. Let
![]() $T_1, \dots, T_l \;:\; \mathbb{T}^m \to \mathbb{T}^m$
be commuting unipotent affine transformations generating an ergodic
$T_1, \dots, T_l \;:\; \mathbb{T}^m \to \mathbb{T}^m$
be commuting unipotent affine transformations generating an ergodic
![]() $\mathbb{Z}^l$
-action. Then the polynomial sequence
$\mathbb{Z}^l$
-action. Then the polynomial sequence
 \begin{align*} \left( \prod_{j=1}^l{T_j^{p_{1,j}(n)}}x, \dots, \prod_{j=1}^l{T_j^{p_{k,j}(n)}}x \right)_{n \in \mathbb{Z}^d} \end{align*}
\begin{align*} \left( \prod_{j=1}^l{T_j^{p_{1,j}(n)}}x, \dots, \prod_{j=1}^l{T_j^{p_{k,j}(n)}}x \right)_{n \in \mathbb{Z}^d} \end{align*}
is well-distributed in
![]() $\mathbb{T}^{mk}$
for all x in a co-meager set of full measure.
$\mathbb{T}^{mk}$
for all x in a co-meager set of full measure.
3·1·2. Equidistribution of
 $\mathbb{Z}^l$
-polynomial sequences
$\mathbb{Z}^l$
-polynomial sequences
In order to prove Theorem 3·8, we will use two classic results in equidistribution. The first is a multivariable version of Weyl’s polynomial equidistribution theorem.
Lemma 3·9 (cf. [
Reference Weyl38
, Satz 20]). Fix
![]() $d \in \mathbb{N}$
. Let
$d \in \mathbb{N}$
. Let
![]() $p(x_1, \dots, x_d) \in \mathbb{R}[x_1, \dots, x_d]$
. If at least one coefficient of p other than the constant term is irrational, then the
$p(x_1, \dots, x_d) \in \mathbb{R}[x_1, \dots, x_d]$
. If at least one coefficient of p other than the constant term is irrational, then the
![]() $\mathbb{Z}^d$
-sequence
$\mathbb{Z}^d$
-sequence
![]() $\left( p(n_1, \dots, n_d) \right)_{n \in \mathbb{Z}^d}$
is well-distributed mod 1.
$\left( p(n_1, \dots, n_d) \right)_{n \in \mathbb{Z}^d}$
is well-distributed mod 1.
Remark 3·10. Weyl proved Lemma 3·9 in the case
![]() $d=2$
, with indications of how to prove the case of general d, for Følner sequences that are increasing dilations of a fixed set. Lemma 3·9 in its full generality is today an easy exercise with the help of an appropriate variant of the van der Corput trick (see, e.g. [
Reference Bergelson and McCutcheon13
, lemma A6]).
$d=2$
, with indications of how to prove the case of general d, for Følner sequences that are increasing dilations of a fixed set. Lemma 3·9 in its full generality is today an easy exercise with the help of an appropriate variant of the van der Corput trick (see, e.g. [
Reference Bergelson and McCutcheon13
, lemma A6]).
The next lemma allows one to reduce equidistribution in a multidimensional torus to equidistribution in the circle.
Lemma 3·11.
Fix
![]() $d, m \in \mathbb{N}$
. A
$d, m \in \mathbb{N}$
. A
![]() $\mathbb{Z}^d$
-sequence
$\mathbb{Z}^d$
-sequence
![]() $u \;:\; \mathbb{Z}^d \to \mathbb{T}^m$
is well-distributed in
$u \;:\; \mathbb{Z}^d \to \mathbb{T}^m$
is well-distributed in
![]() $\mathbb{T}^m$
if and only if for every
$\mathbb{T}^m$
if and only if for every
![]() $c \in \mathbb{Z}^m \setminus \{0\}$
, the sequence
$c \in \mathbb{Z}^m \setminus \{0\}$
, the sequence
![]() $c \cdot u(n) = c_1u_1(n) + \cdots + c_mu_m(n)$
is well-distributed in
$c \cdot u(n) = c_1u_1(n) + \cdots + c_mu_m(n)$
is well-distributed in
![]() $\mathbb{T}$
.
$\mathbb{T}$
.
Proof. See [
Reference Kuipers and Niederreiter33
, theorem 6·3] for the case
![]() $d = 1$
. The same argument works for general
$d = 1$
. The same argument works for general
![]() $d \in \mathbb{N}$
.
$d \in \mathbb{N}$
.
With these two lemmas at hand, we are now ready to prove Theorem 3·8.
Proof of Theorem 3·8. For each
![]() $j = 1, \dots, l$
, we can write
$j = 1, \dots, l$
, we can write
![]() $T_jx = A_jx + \alpha_j$
for some unipotent
$T_jx = A_jx + \alpha_j$
for some unipotent
![]() $(m \times m)$
-matrix
$(m \times m)$
-matrix
![]() $A_j$
with integer entries and a vector
$A_j$
with integer entries and a vector
![]() $\alpha_j \in \mathbb{T}^m$
. Since the matrices
$\alpha_j \in \mathbb{T}^m$
. Since the matrices
![]() $A_1, \dots, A_l$
commute, they are simultaneously triangularisable. That is, there is a matrix P with rational entries and lower-triangular matrices
$A_1, \dots, A_l$
commute, they are simultaneously triangularisable. That is, there is a matrix P with rational entries and lower-triangular matrices
![]() $B_j$
such that
$B_j$
such that
![]() $A_jP = PB_j$
. Multiplying P by a common denominator of its entries, we may assume that P has integer entries. Then P is well-defined as a surjective endomorphism of
$A_jP = PB_j$
. Multiplying P by a common denominator of its entries, we may assume that P has integer entries. Then P is well-defined as a surjective endomorphism of
![]() $\mathbb{T}^m$
. (One can show that in general, P cannot be assumed to be an automorphism.) Let
$\mathbb{T}^m$
. (One can show that in general, P cannot be assumed to be an automorphism.) Let
![]() $\beta_j \in \mathbb{T}^m$
such that
$\beta_j \in \mathbb{T}^m$
such that
![]() $P\beta_j = \alpha_j$
, and set
$P\beta_j = \alpha_j$
, and set
![]() $S_jx \;:\!=\; B_jx + \beta_j$
. Then we have
$S_jx \;:\!=\; B_jx + \beta_j$
. Then we have
![]() $T_jPx = A_jPx + \alpha_j = PB_jx + P\beta_j = PS_jx$
. That is, T is a factor of S with factor map
$T_jPx = A_jPx + \alpha_j = PB_jx + P\beta_j = PS_jx$
. That is, T is a factor of S with factor map
![]() $P \;:\; \mathbb{T}^m \to \mathbb{T}^m$
.
$P \;:\; \mathbb{T}^m \to \mathbb{T}^m$
.
Now we check that S is an ergodic
![]() $\mathbb{Z}^l$
-action on
$\mathbb{Z}^l$
-action on
![]() $\mathbb{T}^m$
. For
$\mathbb{T}^m$
. For
![]() $n = (n_1, \dots, n_l) \in \mathbb{Z}^l$
, let
$n = (n_1, \dots, n_l) \in \mathbb{Z}^l$
, let
![]() $S^n \;:\!=\; \prod_{j=1}^l{S_j^{n_j}}$
and
$S^n \;:\!=\; \prod_{j=1}^l{S_j^{n_j}}$
and
![]() $T^n \;:\!=\; \prod_{j=1}^l{T_j^{n_j}}$
. Suppose
$T^n \;:\!=\; \prod_{j=1}^l{T_j^{n_j}}$
. Suppose
![]() $A \subseteq \mathbb{T}^m$
is S-invariant. That is,
$A \subseteq \mathbb{T}^m$
is S-invariant. That is,
![]() $S^nA = A$
for every
$S^nA = A$
for every
![]() $n \in \mathbb{Z}^l$
. Applying the factor map
$n \in \mathbb{Z}^l$
. Applying the factor map
![]() $P \;:\; \mathbb{T}^m \to \mathbb{T}^m$
, we have
$P \;:\; \mathbb{T}^m \to \mathbb{T}^m$
, we have
![]() $PA = PS^nA = T^nPA$
, so PA is a T-invariant set. But T is ergodic by assumption, so
$PA = PS^nA = T^nPA$
, so PA is a T-invariant set. But T is ergodic by assumption, so
![]() $\mu(PA) \in \{0,1\}$
. If
$\mu(PA) \in \{0,1\}$
. If
![]() $\mu(PA) = 0$
, then
$\mu(PA) = 0$
, then
![]() $\mu(A) \le \mu(P^{-1}PA) = \mu(A) = 0$
. On the other hand, if
$\mu(A) \le \mu(P^{-1}PA) = \mu(A) = 0$
. On the other hand, if
![]() $\mu(PA) = 1$
, then
$\mu(PA) = 1$
, then
![]() $\mu(A) \ge {1}/{|\det(P)|}$
.
$\mu(A) \ge {1}/{|\det(P)|}$
.
Assume A is an S-invariant set of minimal positive measure so that
![]() $\left. S \right|_A \;:\; A \to A$
is ergodic. Let
$\left. S \right|_A \;:\; A \to A$
is ergodic. Let
![]() $x \in A$
be a generic point for
$x \in A$
be a generic point for
![]() $\left. S \right|_A$
. Then by Proposition 2·5, A differs from the set
$\left. S \right|_A$
. Then by Proposition 2·5, A differs from the set
![]() $Y = \overline{\left\{S^nx \;:\; n \in \mathbb{Z}^l\right\}}$
by a null-set, and Y is a subtorus of
$Y = \overline{\left\{S^nx \;:\; n \in \mathbb{Z}^l\right\}}$
by a null-set, and Y is a subtorus of
![]() $\mathbb{T}^m$
. But
$\mathbb{T}^m$
. But
![]() $\mu(Y) = \mu(A) > 0$
, so
$\mu(Y) = \mu(A) > 0$
, so
![]() $Y = \mathbb{T}^m$
. Thus, for any S-invariant set A of positive measure, we have
$Y = \mathbb{T}^m$
. Thus, for any S-invariant set A of positive measure, we have
![]() $\mu(A) = 1$
. Therefore, S is ergodic.
$\mu(A) = 1$
. Therefore, S is ergodic.
The above argument shows that, without loss of generality, we may assume that the transformations
![]() $T_j$
are of the form
$T_j$
are of the form
 \begin{align*} T_jx = \left( x_1 + \alpha^{(j)}_1, x_2 + a^{(j)}_{2,1}x_1 + \alpha^{(j)}_2, \dots, x_m + \sum_{r=1}^{m-1}{a^{(j)}_{m,r}x_r} + \alpha^{(j)}_m \right) \end{align*}
\begin{align*} T_jx = \left( x_1 + \alpha^{(j)}_1, x_2 + a^{(j)}_{2,1}x_1 + \alpha^{(j)}_2, \dots, x_m + \sum_{r=1}^{m-1}{a^{(j)}_{m,r}x_r} + \alpha^{(j)}_m \right) \end{align*}
for
![]() $x = (x_1, \dots, x_m) \in \mathbb{T}^m$
.
$x = (x_1, \dots, x_m) \in \mathbb{T}^m$
.
Let
![]() $u_x(n) \;:\!=\; \left( T^{p_1(n)}x, \dots, T^{p_k(n)}x \right)$
for
$u_x(n) \;:\!=\; \left( T^{p_1(n)}x, \dots, T^{p_k(n)}x \right)$
for
![]() $x \in \mathbb{T}^m$
and
$x \in \mathbb{T}^m$
and
![]() $n \in \mathbb{Z}^d$
, where
$n \in \mathbb{Z}^d$
, where
![]() $T^{p_i(n)}$
denotes the transformation
$T^{p_i(n)}$
denotes the transformation
![]() $\prod_{j=1}^l{T_j^{p_{i,j}(n)}}$
. We now break the proof into two cases, depending on the coefficients
$\prod_{j=1}^l{T_j^{p_{i,j}(n)}}$
. We now break the proof into two cases, depending on the coefficients
![]() $a^{(j)}_{s,r}$
.
$a^{(j)}_{s,r}$
.
First consider the case
![]() $a^{(j)}_{s,r} = 0$
for all
$a^{(j)}_{s,r} = 0$
for all
![]() $1 \le j \le l$
,
$1 \le j \le l$
,
![]() $2 \le s \le m$
, and
$2 \le s \le m$
, and
![]() $1 \le r \le s-1$
. That is,
$1 \le r \le s-1$
. That is,
is a toral rotation for
![]() $j = 1, \dots, l$
. Let
$j = 1, \dots, l$
. Let
![]() $\alpha \;:\; \mathbb{Z}^l \to \mathbb{T}^m$
be the homomorphism
$\alpha \;:\; \mathbb{Z}^l \to \mathbb{T}^m$
be the homomorphism
![]() $\alpha(n_1, \dots, n_l) = \sum_{j=1}^l{n_j\alpha^{(j)}}$
. Then for any
$\alpha(n_1, \dots, n_l) = \sum_{j=1}^l{n_j\alpha^{(j)}}$
. Then for any
![]() $x \in \mathbb{T}^m$
, we have
$x \in \mathbb{T}^m$
, we have
Now let
![]() $(c_{i,s})_{1 \le i \le k, 1 \le s \le m} \in \mathbb{Z}^{mk} \setminus \{0\}$
. By Lemma 3·11, it suffices to show
$(c_{i,s})_{1 \le i \le k, 1 \le s \le m} \in \mathbb{Z}^{mk} \setminus \{0\}$
. By Lemma 3·11, it suffices to show
 \begin{align*} c \cdot u_0(n) = \sum_{i=1}^k{c_i \cdot \alpha(p_i(n))} \end{align*}
\begin{align*} c \cdot u_0(n) = \sum_{i=1}^k{c_i \cdot \alpha(p_i(n))} \end{align*}
is well-distributed in
![]() $\mathbb{T}$
. For each
$\mathbb{T}$
. For each
![]() $i = 1, \dots, k$
and
$i = 1, \dots, k$
and
![]() $n \in \mathbb{Z}^l$
, we have
$n \in \mathbb{Z}^l$
, we have
 \begin{align*} c_i \cdot \alpha(n) = \sum_{s=1}^m{c_{i,s} \sum_{j=1}^l{n_j\alpha^{(j)}_s}} = \sum_{j=1}^l{n_j \sum_{s=1}^m{c_{i,s}\alpha^{(j)}_s}}. \end{align*}
\begin{align*} c_i \cdot \alpha(n) = \sum_{s=1}^m{c_{i,s} \sum_{j=1}^l{n_j\alpha^{(j)}_s}} = \sum_{j=1}^l{n_j \sum_{s=1}^m{c_{i,s}\alpha^{(j)}_s}}. \end{align*}
Letting
![]() $\beta_i = \left( \sum_{s=1}^m{c_{i,s}\alpha^{(1)}_s}, \dots, \sum_{s=1}^m{c_{i,s}\alpha^{(l)}_s} \right) \in \mathbb{T}^l$
, we therefore have
$\beta_i = \left( \sum_{s=1}^m{c_{i,s}\alpha^{(1)}_s}, \dots, \sum_{s=1}^m{c_{i,s}\alpha^{(l)}_s} \right) \in \mathbb{T}^l$
, we therefore have
Thus,
 \begin{align*} c \cdot u_0(n) = \sum_{i=1}^k{\beta_i \cdot p_i(n)} = \sum_{i=1}^k{\sum_{j=1}^l{\beta_{i,j}p_{i,j}(n)}}, \end{align*}
\begin{align*} c \cdot u_0(n) = \sum_{i=1}^k{\beta_i \cdot p_i(n)} = \sum_{i=1}^k{\sum_{j=1}^l{\beta_{i,j}p_{i,j}(n)}}, \end{align*}
which is well-distributed by Lemma 3·9.
Now suppose
![]() $a^{(j)}_{s,r} \ne 0$
for some
$a^{(j)}_{s,r} \ne 0$
for some
![]() $1 \le j \le l, 2 \le s \le m$
, and
$1 \le j \le l, 2 \le s \le m$
, and
![]() $1 \le r \le s-1$
. Let
$1 \le r \le s-1$
. Let
![]() $x = (x_1, \dots, x_m)$
so that
$x = (x_1, \dots, x_m)$
so that
![]() $\{1, x_1, \dots, x_m\}$
is linearly independent over
$\{1, x_1, \dots, x_m\}$
is linearly independent over
![]() $\mathbb{Q} \left( \left\{ \alpha^{(j)}_s \;:\; 1 \le j \le l, 1 \le s \le m \right\} \right)$
.
$\mathbb{Q} \left( \left\{ \alpha^{(j)}_s \;:\; 1 \le j \le l, 1 \le s \le m \right\} \right)$
.
Put
![]() $r_0 \;:\!=\; \max \left\{ 1 \le r \le m-1 \;:\; a^{(j)}_{s,r} \ne 0\;\text{for some}\;1 \le j \le l\;\text{and}\;r+1 \le s \le m \right\}$
, and let
$r_0 \;:\!=\; \max \left\{ 1 \le r \le m-1 \;:\; a^{(j)}_{s,r} \ne 0\;\text{for some}\;1 \le j \le l\;\text{and}\;r+1 \le s \le m \right\}$
, and let
![]() $S \;:\!=\; \left\{ r_0 + 1 \le s \le m \;:\; a^{(j)}_{s,r_0} \ne 0\;\text{for some}\;1 \le j \le l \right\}$
. For
$S \;:\!=\; \left\{ r_0 + 1 \le s \le m \;:\; a^{(j)}_{s,r_0} \ne 0\;\text{for some}\;1 \le j \le l \right\}$
. For
![]() $s \in S$
, let
$s \in S$
, let
We claim that without loss of generality,
![]() $\{v_s \;:\; s \in S\}$
is linearly independent over
$\{v_s \;:\; s \in S\}$
is linearly independent over
![]() $\mathbb{Q}$
. Indeed, suppose
$\mathbb{Q}$
. Indeed, suppose
![]() $\sum_{s \in S}{c_sv_s} = 0$
for some
$\sum_{s \in S}{c_sv_s} = 0$
for some
![]() $(c_s)_{s \in S} \in \mathbb{Z}^S \setminus \{0\}$
. Taking
$(c_s)_{s \in S} \in \mathbb{Z}^S \setminus \{0\}$
. Taking
![]() $s_0 \;:\!=\; \max\{ s \in S \;:\; c_s \ne 0 \}$
, we can perform a change of variables
$s_0 \;:\!=\; \max\{ s \in S \;:\; c_s \ne 0 \}$
, we can perform a change of variables
In the new coordinates, this gives
![]() $\widetilde{v}_{s_0} = 0$
, so
$\widetilde{v}_{s_0} = 0$
, so
![]() $\widetilde{S} = S \setminus \{s_0\}$
and linear dependence is removed. Moreover, this change of variables is
$\widetilde{S} = S \setminus \{s_0\}$
and linear dependence is removed. Moreover, this change of variables is
![]() $|c_{s_0}|$
-to-one, so well-distribution in the new coordinates implies well-distribution in the original system, since orbit closures of polynomial sequences must be finite unions of subtori (see Proposition 2·5).
$|c_{s_0}|$
-to-one, so well-distribution in the new coordinates implies well-distribution in the original system, since orbit closures of polynomial sequences must be finite unions of subtori (see Proposition 2·5).
Assume now that
![]() $\{v_s \;:\; s \in S\}$
is linearly independent over
$\{v_s \;:\; s \in S\}$
is linearly independent over
![]() $\mathbb{Q}$
. Let
$\mathbb{Q}$
. Let
![]() $(c_{i,s})_{1 \le i \le k, 1 \le s \le m} \in \mathbb{Z}^{mk} \setminus \{0\}$
. If
$(c_{i,s})_{1 \le i \le k, 1 \le s \le m} \in \mathbb{Z}^{mk} \setminus \{0\}$
. If
![]() $c_{i,s} = 0$
for
$c_{i,s} = 0$
for
![]() $1 \le i \le k$
and
$1 \le i \le k$
and
![]() $s \in S$
, then we can reduce to the lower-dimensional torus consisting of those coordinates not in the set S. Thus, we may assume
$s \in S$
, then we can reduce to the lower-dimensional torus consisting of those coordinates not in the set S. Thus, we may assume
![]() $c_{i,s} \ne 0$
for some
$c_{i,s} \ne 0$
for some
![]() $1 \le i \le k$
and
$1 \le i \le k$
and
![]() $s \in S$
. Now expand
$s \in S$
. Now expand
where
![]() $P_s$
is
$P_s$
is
![]() $\mathbb{Z}$
-valued for each
$\mathbb{Z}$
-valued for each
![]() $s = 1, \dots, m$
and R(n) is linearly independent from
$s = 1, \dots, m$
and R(n) is linearly independent from
![]() $\{x_1, \dots, x_s\}$
over
$\{x_1, \dots, x_s\}$
over
![]() $\mathbb{Q}$
for every
$\mathbb{Q}$
for every
![]() $n \in \mathbb{Z}^d$
. By the restriction on the coordinates of x, we can compute
$n \in \mathbb{Z}^d$
. By the restriction on the coordinates of x, we can compute
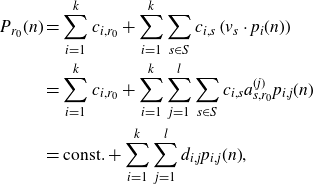 \begin{align*} P_{r_0}(n) & = \sum_{i=1}^k{c_{i,r_0}} + \sum_{i=1}^k{\sum_{s \in S}{c_{i,s} \left( v_s \cdot p_i(n) \right)}} \\ & = \sum_{i=1}^k{c_{i,r_0}} + \sum_{i=1}^k{\sum_{j=1}^l{\sum_{s \in S}{c_{i,s}a^{(j)}_{s,r_0}p_{i,j}(n)}}} \\ & = \text{const.} + \sum_{i=1}^k{\sum_{j=1}^l{d_{i,j}p_{i,j}(n)}}, \end{align*}
\begin{align*} P_{r_0}(n) & = \sum_{i=1}^k{c_{i,r_0}} + \sum_{i=1}^k{\sum_{s \in S}{c_{i,s} \left( v_s \cdot p_i(n) \right)}} \\ & = \sum_{i=1}^k{c_{i,r_0}} + \sum_{i=1}^k{\sum_{j=1}^l{\sum_{s \in S}{c_{i,s}a^{(j)}_{s,r_0}p_{i,j}(n)}}} \\ & = \text{const.} + \sum_{i=1}^k{\sum_{j=1}^l{d_{i,j}p_{i,j}(n)}}, \end{align*}
where
for
![]() $1 \le i \le k$
. By assumption,
$1 \le i \le k$
. By assumption,
![]() $(c_{i,s})_{1 \le i \le k, s \in S} \ne 0$
. Since
$(c_{i,s})_{1 \le i \le k, s \in S} \ne 0$
. Since
![]() $\{v_s \;:\; s \in S\}$
is linearly independent over
$\{v_s \;:\; s \in S\}$
is linearly independent over
![]() $\mathbb{Q}$
, this implies that
$\mathbb{Q}$
, this implies that
![]() $d_{i,j} \ne 0$
for some
$d_{i,j} \ne 0$
for some
![]() $1 \le i \le k$
and
$1 \le i \le k$
and
![]() $1 \le j \le l$
. Therefore,
$1 \le j \le l$
. Therefore,
![]() $P_{r_0}(n)$
is nonconstant, since
$P_{r_0}(n)$
is nonconstant, since
![]() $\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le l\}$
is an independent family. It follows that the polynomial
$\{p_{i,j} \;:\; 1 \le i \le k, 1 \le j \le l\}$
is an independent family. It follows that the polynomial
![]() $c \cdot u_x(n)$
has at least one irrational coefficient other than the constant term, so
$c \cdot u_x(n)$
has at least one irrational coefficient other than the constant term, so
![]() $c \cdot u_x(n)$
is well-distributed in
$c \cdot u_x(n)$
is well-distributed in
![]() $\mathbb{T}$
by Lemma 3·9.
$\mathbb{T}$
by Lemma 3·9.
We have shown that
![]() $c \cdot u_x(n)$
is well-distributed in
$c \cdot u_x(n)$
is well-distributed in
![]() $\mathbb{T}$
for every
$\mathbb{T}$
for every
![]() $c \in \mathbb{Z}^{mk} \setminus \{0\}$
. By Lemma 3·11, it follows that
$c \in \mathbb{Z}^{mk} \setminus \{0\}$
. By Lemma 3·11, it follows that
![]() $u_x(n)$
is well-distributed in
$u_x(n)$
is well-distributed in
![]() $\mathbb{T}^{mk}$
as desired.
$\mathbb{T}^{mk}$
as desired.
Let E be the set of exceptional points
![]() $x \in \mathbb{T}^m$
such that
$x \in \mathbb{T}^m$
such that
![]() $\left( u_x(n) \right)_{n \in \mathbb{Z}^d}$
is not well-distributed in
$\left( u_x(n) \right)_{n \in \mathbb{Z}^d}$
is not well-distributed in
![]() $\mathbb{T}^{mk}$
. The above argument show that if
$\mathbb{T}^{mk}$
. The above argument show that if
![]() $x = (x_1, \dots, x_m) \in E$
, then
$x = (x_1, \dots, x_m) \in E$
, then
for some coefficients
For each such choice of coefficients
![]() $(c_r)_{r=0}^m$
, the equation (3·1) defines a subtorus of dimension
$(c_r)_{r=0}^m$
, the equation (3·1) defines a subtorus of dimension
![]() $m-1$
. Hence, E is contained in a countable union of
$m-1$
. Hence, E is contained in a countable union of
![]() $(m-1)$
-dimensional subtori. In particular, E is both a set of measure zero and meager in
$(m-1)$
-dimensional subtori. In particular, E is both a set of measure zero and meager in
![]() $\mathbb{T}^m$
.
$\mathbb{T}^m$
.
3·1·3. The general case
Theorem 3·1 says the for totally ergodic systems, the trivial factor is characteristic for independent polynomials
![]() $\{p_1, \dots, p_k\}$
. In particular, the Kronecker factor
$\{p_1, \dots, p_k\}$
. In particular, the Kronecker factor
![]() $\mathcal{Z} = \mathcal{Z}_1$
is characteristic. Now, the collection of all families of independent
$\mathcal{Z} = \mathcal{Z}_1$
is characteristic. Now, the collection of all families of independent
![]() $\mathcal{O}_K$
-valued polynomials is clearly eligible, so by Proposition 2·13, the Kronecker factor is characteristic for independent polynomials in any ergodic system.
$\mathcal{O}_K$
-valued polynomials is clearly eligible, so by Proposition 2·13, the Kronecker factor is characteristic for independent polynomials in any ergodic system.
In order to prove Theorem C, it remains only to reduce from the Kronecker factor to the rational Kronecker factor. We want to prove: if
![]() $\mathbb{E}\left[ {f_i} \mid {\mathcal{K}_{rat}} \right] = 0$
for some
$\mathbb{E}\left[ {f_i} \mid {\mathcal{K}_{rat}} \right] = 0$
for some
![]() $i = 1, \dots, k$
, then
$i = 1, \dots, k$
, then
![]() $\text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = 0$
. Since the Kronecker factor is spanned by eigenfunctions, we may assume that
$\text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = 0$
. Since the Kronecker factor is spanned by eigenfunctions, we may assume that
![]() $f_i$
is an eigenfunction with eigenvalue
$f_i$
is an eigenfunction with eigenvalue
![]() $\alpha_i \in \mathbb{T}^d$
for
$\alpha_i \in \mathbb{T}^d$
for
![]() $i = 1, \dots, k$
. That is,
$i = 1, \dots, k$
. That is,
![]() $T^nf_i = e(n \cdot \alpha_i)f_i$
. The condition that
$T^nf_i = e(n \cdot \alpha_i)f_i$
. The condition that
![]() $\mathbb{E}\left[ {f_i} \mid {\mathcal{K}_{rat}} \right] = 0$
means that
$\mathbb{E}\left[ {f_i} \mid {\mathcal{K}_{rat}} \right] = 0$
means that
![]() $\alpha_i \notin \mathbb{Q}^d$
for some
$\alpha_i \notin \mathbb{Q}^d$
for some
![]() $i = 1, \dots, k$
. Expanding the multiple ergodic average, we have
$i = 1, \dots, k$
. Expanding the multiple ergodic average, we have
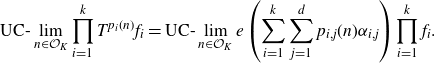 \begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = \text{UC-}\lim_{n \in \mathcal{O}_K}{e \left( \sum_{i=1}^k{\sum_{j=1}^d{p_{i,j}(n) \alpha_{i,j}}} \right) \prod_{i=1}^k{f_i}}.\end{align}
\begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^k{T^{p_i(n)}f_i}} = \text{UC-}\lim_{n \in \mathcal{O}_K}{e \left( \sum_{i=1}^k{\sum_{j=1}^d{p_{i,j}(n) \alpha_{i,j}}} \right) \prod_{i=1}^k{f_i}}.\end{align}
Since
![]() $\alpha_{i,j} \notin \mathbb{Q}$
for some
$\alpha_{i,j} \notin \mathbb{Q}$
for some
![]() $1 \le i \le k$
and
$1 \le i \le k$
and
![]() $1 \le j \le d$
, the polynomial
$1 \le j \le d$
, the polynomial
![]() $\sum_{i=1}^k{\sum_{j=1}^d{p_{i,j}(n)\alpha_{i,j}}}$
has an irrational coefficient other than the constant term. Thus, by Lemma 3·9, the average (3·2) is equal to 0 as desired.
$\sum_{i=1}^k{\sum_{j=1}^d{p_{i,j}(n)\alpha_{i,j}}}$
has an irrational coefficient other than the constant term. Thus, by Lemma 3·9, the average (3·2) is equal to 0 as desired.
3·2. Proof of Theorem D
We follow the approach of Frantzikinakis (see [ Reference Frantzikinakis19 , theorem A]), modifying as necessary to upgrade to our multidimensional setting.
The polynomials
![]() $l_1p(n), \dots, l_kp(n)$
are essentially distinct, so the characteristic factor for the averages
$l_1p(n), \dots, l_kp(n)$
are essentially distinct, so the characteristic factor for the averages
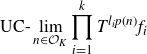 \begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{l_ip(n)}f_i} }\end{align}
\begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{l_ip(n)}f_i} }\end{align}
is a nilfactor,
![]() $\mathcal{Z}_r$
, for some
$\mathcal{Z}_r$
, for some
![]() $r \in \mathbb{Z}$
, by Theorem 1·13. The content of Theorem D is thus to show that
$r \in \mathbb{Z}$
, by Theorem 1·13. The content of Theorem D is thus to show that
![]() $r = k-1$
.
$r = k-1$
.
We do this in several steps. First, we will show that for totally ergodic systems, the limit (3·3) does not depend on p. As a consequence,
![]() $\mathcal{Z}_{k-1}$
is characteristic for totally ergodic systems, since it is characteristic when
$\mathcal{Z}_{k-1}$
is characteristic for totally ergodic systems, since it is characteristic when
![]() $p(n) = n$
. We then apply Proposition 2·13 to conclude that
$p(n) = n$
. We then apply Proposition 2·13 to conclude that
![]() $\mathcal{Z}_{k-1}$
is characteristic in any ergodic system.
$\mathcal{Z}_{k-1}$
is characteristic in any ergodic system.
3·2·1. Totally ergodic systems
For this section, we will assume that
![]() $\left( X, \mathcal{B}, \mu, T \right)$
is a totally ergodic
$\left( X, \mathcal{B}, \mu, T \right)$
is a totally ergodic
![]() $\mathcal{O}_K$
-system, and we set out to prove that the limit (3·3) is independent of the choice of polynomial p.
$\mathcal{O}_K$
-system, and we set out to prove that the limit (3·3) is independent of the choice of polynomial p.
By Theorem 1·13 and a standard approximation argument, we may further assume that
![]() $X = G/\Gamma$
is a nilmanifold and T is an action by niltranslations
$X = G/\Gamma$
is a nilmanifold and T is an action by niltranslations
![]() $T^nx = a(n)x$
with
$T^nx = a(n)x$
with
![]() $a(n) \in G$
. It therefore suffices to show that the orbits
$a(n) \in G$
. It therefore suffices to show that the orbits
![]() $\left\{\left( T^{l_1p(n)}x, \dots, T^{l_kp(n)}x \right) \;:\; n \in \mathcal{O}_K\right\}$
and
$\left\{\left( T^{l_1p(n)}x, \dots, T^{l_kp(n)}x \right) \;:\; n \in \mathcal{O}_K\right\}$
and
![]() $\left\{\left( T^{l_1n}x, \dots, T^{l_kn}x \right) \;:\; n \in \mathcal{O}_K\right\}$
are equidistributed for almost every
$\left\{\left( T^{l_1n}x, \dots, T^{l_kn}x \right) \;:\; n \in \mathcal{O}_K\right\}$
are equidistributed for almost every
![]() $x \in X$
. Equivalently, letting
$x \in X$
. Equivalently, letting
![]() $g(n) \;:\!=\; \left( a(l_1n), \dots, a(l_kn) \right) \in G^k$
and
$g(n) \;:\!=\; \left( a(l_1n), \dots, a(l_kn) \right) \in G^k$
and
![]() $\widetilde{x} = (x, \dots, x) \in X^k$
, we want to show that
$\widetilde{x} = (x, \dots, x) \in X^k$
, we want to show that
![]() $\left\{ g(p(n))\widetilde{x} \;:\; n \in \mathcal{O}_K \right\}$
and
$\left\{ g(p(n))\widetilde{x} \;:\; n \in \mathcal{O}_K \right\}$
and
![]() $\left\{ g(n)\widetilde{x} \;:\; n \in \mathcal{O}_K \right\}$
are equidistributed for almost every
$\left\{ g(n)\widetilde{x} \;:\; n \in \mathcal{O}_K \right\}$
are equidistributed for almost every
![]() $x \in X$
. Now, by Theorem 3·5, it is enough to show that these sequences have the same closure in
$x \in X$
. Now, by Theorem 3·5, it is enough to show that these sequences have the same closure in
![]() $X^k$
.
$X^k$
.
By Proposition 2·9, any nonconstant polynomial
![]() $p \in K[x]$
has algebraically independent coordinates, so we will prove a related result about
$p \in K[x]$
has algebraically independent coordinates, so we will prove a related result about
![]() $\mathbb{Z}^d$
-valued polynomials with algebraically independent coordinates:
$\mathbb{Z}^d$
-valued polynomials with algebraically independent coordinates:
Proposition 3·12 (cf. [
Reference Frantzikinakis19
, Proposition 2·7]). Let
![]() $X = G/\Gamma$
be a nilmanifold,
$X = G/\Gamma$
be a nilmanifold,
![]() $g \;:\; \mathbb{Z}^l \to G$
a polynomial sequence, and
$g \;:\; \mathbb{Z}^l \to G$
a polynomial sequence, and
![]() $x \in X$
. Suppose
$x \in X$
. Suppose
![]() $p \;:\; \mathbb{Z}^d \to \mathbb{Z}^l$
is a polynomial with algebraically independent coordinates. If
$p \;:\; \mathbb{Z}^d \to \mathbb{Z}^l$
is a polynomial with algebraically independent coordinates. If
![]() $Y \;:\!=\; \overline{\left\{ g(n)x \;:\; n \in \mathbb{Z}^l \right\}}$
is connected, then
$Y \;:\!=\; \overline{\left\{ g(n)x \;:\; n \in \mathbb{Z}^l \right\}}$
is connected, then
![]() $\overline{\left\{ g(p(n))x \;:\; n \in \mathbb{Z}^d \right\}} = Y$
.
$\overline{\left\{ g(p(n))x \;:\; n \in \mathbb{Z}^d \right\}} = Y$
.
Proof. By Theorem 2·6, Y is a subnilmanifold
![]() $H/\Delta$
. Now by Theorem 3·5, we may replace H by
$H/\Delta$
. Now by Theorem 3·5, we may replace H by
![]() $H/[H_0,H_0]$
and assume that
$H/[H_0,H_0]$
and assume that
![]() $H_0$
is abelian. As in Lemma 3·7, we may further reduce to the case that
$H_0$
is abelian. As in Lemma 3·7, we may further reduce to the case that
![]() $Y = \mathbb{T}^m$
and
$Y = \mathbb{T}^m$
and
![]() $g(n)x = T_1^{p_1(n)} \cdots T_k^{p_k(n)}x$
with
$g(n)x = T_1^{p_1(n)} \cdots T_k^{p_k(n)}x$
with
![]() $T_i$
unipotent affine actions. The coordinates of
$T_i$
unipotent affine actions. The coordinates of
![]() $\left\{ g(n)x \;:\; n \in \mathbb{Z}^l \right\}$
are real polynomials in
$\left\{ g(n)x \;:\; n \in \mathbb{Z}^l \right\}$
are real polynomials in
![]() $n \in \mathbb{Z}^l$
, so it remains to show: if
$n \in \mathbb{Z}^l$
, so it remains to show: if
![]() $u \;:\; \mathbb{Z}^l \to \mathbb{T}^m$
is a sequence with polynomial coordinates and
$u \;:\; \mathbb{Z}^l \to \mathbb{T}^m$
is a sequence with polynomial coordinates and
![]() $\overline{\left\{ u(n) \;:\; n \in \mathbb{Z}^l \right\}} = \mathbb{T}^m$
, then
$\overline{\left\{ u(n) \;:\; n \in \mathbb{Z}^l \right\}} = \mathbb{T}^m$
, then
![]() $\overline{\left\{ u(p(n)) \;:\; n \in \mathbb{Z}^d \right\}} = \mathbb{T}^m$
for every polynomial
$\overline{\left\{ u(p(n)) \;:\; n \in \mathbb{Z}^d \right\}} = \mathbb{T}^m$
for every polynomial
![]() $p \;:\; \mathbb{Z}^d \to \mathbb{Z}^l$
with algebraically independent coordinates.
$p \;:\; \mathbb{Z}^d \to \mathbb{Z}^l$
with algebraically independent coordinates.
The polynomial u(n) can be decomposed as
![]() $u(n) = u(0) + u_0(n)q + u_1(n)\alpha_1 + \cdots + u_r(n)\alpha_r$
, where
$u(n) = u(0) + u_0(n)q + u_1(n)\alpha_1 + \cdots + u_r(n)\alpha_r$
, where
![]() $q \in \mathbb{Q}$
,
$q \in \mathbb{Q}$
,
![]() $\alpha_1, \dots, \alpha_r \in \mathbb{R}$
are linearly independent irrational numbers and
$\alpha_1, \dots, \alpha_r \in \mathbb{R}$
are linearly independent irrational numbers and
![]() $u_i \;:\; \mathbb{Z}^l \to \mathbb{Z}^m$
are polynomials with
$u_i \;:\; \mathbb{Z}^l \to \mathbb{Z}^m$
are polynomials with
![]() $u_i(0) = 0$
. By Corollary 2·7, the orbit
$u_i(0) = 0$
. By Corollary 2·7, the orbit
![]() $\left\{ u(n) \;:\; n \in \mathbb{Z}^l \right\}$
is dense in
$\left\{ u(n) \;:\; n \in \mathbb{Z}^l \right\}$
is dense in
![]() $\mathbb{T}^m$
if and only if
$\mathbb{T}^m$
if and only if
Thus, it suffices to prove
![]() $\text{span}(u_i \circ p) = \text{span}(u_i)$
for each
$\text{span}(u_i \circ p) = \text{span}(u_i)$
for each
![]() $i = 1, \dots, r$
.
$i = 1, \dots, r$
.
Fix
![]() $1 \le i \le r$
. Suppose the coordinates of
$1 \le i \le r$
. Suppose the coordinates of
![]() $u_i \circ p$
satisfy a linear relation
$u_i \circ p$
satisfy a linear relation
![]() $\sum_{j=1}^m{c_ju_{i,j}(p(n))} = 0$
for some
$\sum_{j=1}^m{c_ju_{i,j}(p(n))} = 0$
for some
![]() $c_1, \dots, c_m \in \mathbb{Z}$
, where
$c_1, \dots, c_m \in \mathbb{Z}$
, where
![]() $u_i = (u_{i,1}, \dots, u_{i,m})$
with
$u_i = (u_{i,1}, \dots, u_{i,m})$
with
![]() $u_{i,j} \;:\; \mathbb{Z}^l \to \mathbb{Z}$
. Let
$u_{i,j} \;:\; \mathbb{Z}^l \to \mathbb{Z}$
. Let
![]() $v \;:\; \mathbb{Z}^l \to \mathbb{Z}$
be the polynomial
$v \;:\; \mathbb{Z}^l \to \mathbb{Z}$
be the polynomial
![]() $v(n) \;:\!=\; \sum_{j=1}^m{c_ju_{i,j}(n)}$
. Then
$v(n) \;:\!=\; \sum_{j=1}^m{c_ju_{i,j}(n)}$
. Then
![]() $v \circ p = 0$
. But the coordinates of p are algebraically independent, so we must have
$v \circ p = 0$
. But the coordinates of p are algebraically independent, so we must have
![]() $v = 0$
. That is, the coordinates of
$v = 0$
. That is, the coordinates of
![]() $u_i$
satisfies the the same linear relation. Therefore,
$u_i$
satisfies the the same linear relation. Therefore,
![]() $\text{span}(u_i \circ p) = \text{span}(u_i)$
as desired.
$\text{span}(u_i \circ p) = \text{span}(u_i)$
as desired.
It remains only to show that
![]() $Y \;:\!=\; \overline{\left\{ g(n) \widetilde{x} \;:\; n \in \mathcal{O}_K \right\}}$
is connected. This is where we use that the system is totally ergodic. Let
$Y \;:\!=\; \overline{\left\{ g(n) \widetilde{x} \;:\; n \in \mathcal{O}_K \right\}}$
is connected. This is where we use that the system is totally ergodic. Let
![]() $Y_w = Hx_w$
,
$Y_w = Hx_w$
,
![]() $w \in W$
, as in Theorem 2·6. Since W is a finite group,
$w \in W$
, as in Theorem 2·6. Since W is a finite group,
![]() $\omega^{-1}(0) \subseteq \mathbb{Z}^d$
has finite index in
$\omega^{-1}(0) \subseteq \mathbb{Z}^d$
has finite index in
![]() $\mathbb{Z}^d$
. Because T is totally ergodic, we therefore have
$\mathbb{Z}^d$
. Because T is totally ergodic, we therefore have
![]() $Y_0 = Y$
, so Y is indeed connected.
$Y_0 = Y$
, so Y is indeed connected.
In summary, we have shown the following:
Theorem 3·13.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\left( X, \mathcal{B}, \mu, T \right)$
be a totally ergodic
$\left( X, \mathcal{B}, \mu, T \right)$
be a totally ergodic
![]() $\mathcal{O}_K$
-system. Let
$\mathcal{O}_K$
-system. Let
![]() $p(x) \in K[x]$
be a non-constant
$p(x) \in K[x]$
be a non-constant
![]() $\mathcal{O}_K$
-valued polynomial. Let
$\mathcal{O}_K$
-valued polynomial. Let
![]() $l_1, \dots, l_k \in \mathcal{O}_K$
be distinct and nonzero. Then
$l_1, \dots, l_k \in \mathcal{O}_K$
be distinct and nonzero. Then
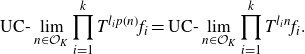 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{l_ip(n)}f_i} } = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{l_in}f_i} }. \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{l_ip(n)}f_i} } = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \prod_{i=1}^k{T^{l_in}f_i} }. \end{align*}
3·2·2. General case
Now we prove Theorem D. Letting
![]() $l \;:\!=\; \gcd(l_1, \dots, l_k)$
and replacing
$l \;:\!=\; \gcd(l_1, \dots, l_k)$
and replacing
![]() $l_1, \dots, l_k$
by
$l_1, \dots, l_k$
by
![]() $l'_i \;:\!=\; {l_i}/{l}$
and p by lp, we may assume without loss of generality that
$l'_i \;:\!=\; {l_i}/{l}$
and p by lp, we may assume without loss of generality that
![]() $l = 1$
. By [
Reference Griesmer27
, theorem 4·1·2], the characteristic factor for
$l = 1$
. By [
Reference Griesmer27
, theorem 4·1·2], the characteristic factor for
![]() $\{l_1n, \dots, l_kn\}$
is
$\{l_1n, \dots, l_kn\}$
is
![]() $\mathcal{Z}_{k-1}$
. Thus, by Theorem 3·13,
$\mathcal{Z}_{k-1}$
. Thus, by Theorem 3·13,
![]() $\mathcal{Z}_{k-1}$
is characteristic for
$\mathcal{Z}_{k-1}$
is characteristic for
![]() $\{l_1p(n), \dots, l_kp(n)\}$
in the case of totally ergodic systems. It is easily checked that the collection
$\{l_1p(n), \dots, l_kp(n)\}$
in the case of totally ergodic systems. It is easily checked that the collection
is eligible (see Definition 2·12) under the assumption that
![]() $l = \gcd(l_1, \dots, l_k) = 1$
. Hence, Theorem D follows by Proposition 2·13.
$l = \gcd(l_1, \dots, l_k) = 1$
. Hence, Theorem D follows by Proposition 2·13.
4. Large intersections
Having established characteristic factors for the polynomial multiple ergodic averages of interest, we now move to deducing the related Khintchine-type theorems.
4·1. Proof of Theorem A
We want to prove Theorem A, restated here for the convenience of the reader:
Theorem A.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
$\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
![]() $\mathcal{O}_K$
-valued polynomials. Then for any measure-preserving
$\mathcal{O}_K$
-valued polynomials. Then for any measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
,
$\left( X, \mathcal{B}, \mu, T \right)$
,
![]() $A \in \mathcal{B}$
, and
$A \in \mathcal{B}$
, and
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is syndetic.
We will prove the following stronger statement:
Theorem 4·1.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Suppose
$\mathcal{O}_K$
. Suppose
![]() $\{p_1, \dots, p_k\} \subseteq K[x]$
is a jointly intersective family of linearly independent
$\{p_1, \dots, p_k\} \subseteq K[x]$
is a jointly intersective family of linearly independent
![]() $\mathcal{O}_K$
-valued polynomials. Then for any measure-preserving
$\mathcal{O}_K$
-valued polynomials. Then for any measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
,
$\left( X, \mathcal{B}, \mu, T \right)$
,
![]() $A \in \mathcal{B}$
, and
$A \in \mathcal{B}$
, and
![]() $\varepsilon > 0$
, there exist
$\varepsilon > 0$
, there exist
![]() $\xi \in \mathcal{O}_K$
and
$\xi \in \mathcal{O}_K$
and
![]() $D \in \mathcal{O}_K \setminus \{0\}$
such that
$D \in \mathcal{O}_K \setminus \{0\}$
such that
Assuming Theorem 4·1, the set
is syndetic by Proposition 1·12. Since
![]() $\xi + D\mathcal{O}_K$
is syndetic in
$\xi + D\mathcal{O}_K$
is syndetic in
![]() $\mathcal{O}_K$
, Theorem 4·1 follows immediately.
$\mathcal{O}_K$
, Theorem 4·1 follows immediately.
Proof of Theorem 4·1. First assume that T is ergodic. The rational Kronecker factor
![]() $\mathcal{K}_{rat}$
is the inverse limit of the periodic factors
$\mathcal{K}_{rat}$
is the inverse limit of the periodic factors
![]() $\mathcal{K}_r \;:\!=\; \left\{ f \in L^2(\mu) \;:\; T^{rn}f = f\;\text{for all}\;n \in \mathcal{O}_K \right\}$
,
$\mathcal{K}_r \;:\!=\; \left\{ f \in L^2(\mu) \;:\; T^{rn}f = f\;\text{for all}\;n \in \mathcal{O}_K \right\}$
,
![]() $r \in \mathcal{O}_K$
. Note that
$r \in \mathcal{O}_K$
. Note that
![]() $\mathcal{K}_r \subseteq \mathcal{K}_s$
if
$\mathcal{K}_r \subseteq \mathcal{K}_s$
if
![]() $r \mid s$
in
$r \mid s$
in
![]() $\mathcal{O}_K$
. Thus, we may approximate
$\mathcal{O}_K$
. Thus, we may approximate
![]() $\mathcal{K}_{rat}$
by
$\mathcal{K}_{rat}$
by
![]() $\mathcal{K}_r$
for some
$\mathcal{K}_r$
for some
![]() $r \in \mathcal{O}_K$
. To be precise, there exists
$r \in \mathcal{O}_K$
. To be precise, there exists
![]() $r \in \mathcal{O}_K$
such that
$r \in \mathcal{O}_K$
such that
Now, the system
![]() $\left( X, \mathcal{B}, \mu, (T^{rn})_{n \in \mathcal{O}_K} \right)$
has finitely many ergodic components. In fact, for some
$\left( X, \mathcal{B}, \mu, (T^{rn})_{n \in \mathcal{O}_K} \right)$
has finitely many ergodic components. In fact, for some
![]() $m \le [\mathcal{O}_K \;:\; r\mathcal{O}_K]$
, X can be partitioned into m disjoint sets
$m \le [\mathcal{O}_K \;:\; r\mathcal{O}_K]$
, X can be partitioned into m disjoint sets
![]() $X_1, \dots, X_m \in \mathcal{B}$
with
$X_1, \dots, X_m \in \mathcal{B}$
with
![]() $\mu(X_j) = {1}/{m}$
such that
$\mu(X_j) = {1}/{m}$
such that
![]() $\mu \left( X_j \triangle T^{-rn}X_j \right) = 0$
and
$\mu \left( X_j \triangle T^{-rn}X_j \right) = 0$
and
![]() $\left( X, \mathcal{B}, \mu_j, (T^{rn})_{n \in \mathcal{O}_K} \right)$
is ergodic, where
$\left( X, \mathcal{B}, \mu_j, (T^{rn})_{n \in \mathcal{O}_K} \right)$
is ergodic, where
![]() $\mu_j(B) = m \cdot \mu(B \cap X_j)$
.
$\mu_j(B) = m \cdot \mu(B \cap X_j)$
.
By Lemma 2·11, let
![]() $\xi \in \mathcal{O}_K$
and
$\xi \in \mathcal{O}_K$
and
![]() $D \in \mathcal{O}_K \setminus \{0\}$
such that
$D \in \mathcal{O}_K \setminus \{0\}$
such that
![]() $p_i(\xi + D\mathcal{O}_K) \subseteq r\mathcal{O}_K$
for
$p_i(\xi + D\mathcal{O}_K) \subseteq r\mathcal{O}_K$
for
![]() $i = 1, \dots, k$
. For each
$i = 1, \dots, k$
. For each
![]() $i = 1, \dots, k$
, let
$i = 1, \dots, k$
, let
![]() $q_i(x) \in K[x]$
be the
$q_i(x) \in K[x]$
be the
![]() $\mathcal{O}_K$
-valued polynomial
$\mathcal{O}_K$
-valued polynomial
![]() $q_i(x) \;:\!=\; r^{-1} p_i(\xi + Dx)$
. Then by Theorem C,
$q_i(x) \;:\!=\; r^{-1} p_i(\xi + Dx)$
. Then by Theorem C,
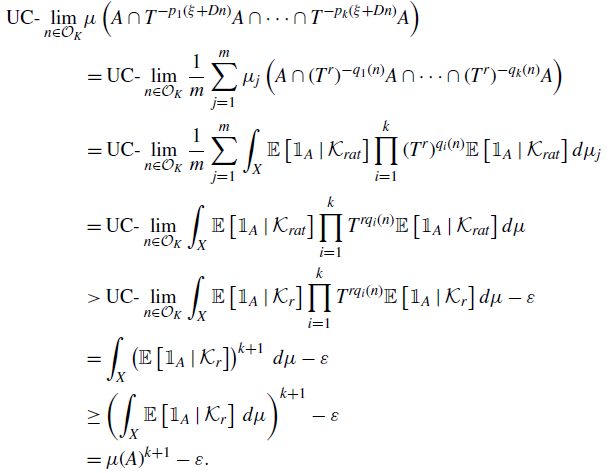 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}&{\mu \left( A \cap T^{-p_1(\xi + Dn)}A \cap \cdots \cap T^{-p_k(\xi + Dn)}A \right)} \\ & = \text{UC-}\lim_{n \in \mathcal{O}_K}{\frac{1}{m} \sum_{j=1}^m{ \mu_j \left( A \cap (T^r)^{-q_1(n)}A \cap \cdots \cap (T^r)^{-q_k(n)}A \right)}} \\ & = \text{UC-}\lim_{n \in \mathcal{O}_K}{\frac{1}{m} \sum_{j=1}^m{ \int_X{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_{rat}} \right] \prod_{i=1}^k{(T^r)^{q_i(n)}\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_{rat}} \right]}\;d\mu_j}}} \\ & = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \int_X{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_{rat}} \right] \prod_{i=1}^k{T^{rq_i(n)}\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_{rat}} \right]}\;d\mu}} \\ & > \text{UC-}\lim_{n \in \mathcal{O}_K}{ \int_X{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_r} \right] \prod_{i=1}^k{T^{rq_i(n)}\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_r} \right]}\;d\mu}} - \varepsilon \\ & = \int_X{ \left( \mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_r} \right] \right)^{k+1}\;d\mu} - \varepsilon \\ & \ge \left( \int_X{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_r} \right]\;d\mu} \right)^{k+1} - \varepsilon \\ & = \mu(A)^{k+1} - \varepsilon. \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}&{\mu \left( A \cap T^{-p_1(\xi + Dn)}A \cap \cdots \cap T^{-p_k(\xi + Dn)}A \right)} \\ & = \text{UC-}\lim_{n \in \mathcal{O}_K}{\frac{1}{m} \sum_{j=1}^m{ \mu_j \left( A \cap (T^r)^{-q_1(n)}A \cap \cdots \cap (T^r)^{-q_k(n)}A \right)}} \\ & = \text{UC-}\lim_{n \in \mathcal{O}_K}{\frac{1}{m} \sum_{j=1}^m{ \int_X{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_{rat}} \right] \prod_{i=1}^k{(T^r)^{q_i(n)}\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_{rat}} \right]}\;d\mu_j}}} \\ & = \text{UC-}\lim_{n \in \mathcal{O}_K}{ \int_X{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_{rat}} \right] \prod_{i=1}^k{T^{rq_i(n)}\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_{rat}} \right]}\;d\mu}} \\ & > \text{UC-}\lim_{n \in \mathcal{O}_K}{ \int_X{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_r} \right] \prod_{i=1}^k{T^{rq_i(n)}\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_r} \right]}\;d\mu}} - \varepsilon \\ & = \int_X{ \left( \mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_r} \right] \right)^{k+1}\;d\mu} - \varepsilon \\ & \ge \left( \int_X{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{K}_r} \right]\;d\mu} \right)^{k+1} - \varepsilon \\ & = \mu(A)^{k+1} - \varepsilon. \end{align*}
Now suppose T is not ergodic. Let
![]() $\mu = \int_{\Omega}{\mu_{\omega}\;d\rho(\omega)}$
be the ergodic decomposition. For each
$\mu = \int_{\Omega}{\mu_{\omega}\;d\rho(\omega)}$
be the ergodic decomposition. For each
![]() $\omega \in \Omega$
, let
$\omega \in \Omega$
, let
![]() $r_{\omega} \in \mathcal{O}_K$
be minimal (with respect to divisibility) so that
$r_{\omega} \in \mathcal{O}_K$
be minimal (with respect to divisibility) so that
The function
![]() $\omega \mapsto r_{\omega}$
is measurable, so we may define
$\omega \mapsto r_{\omega}$
is measurable, so we may define
![]() $\Omega_r \;:\!=\; \{\omega \in \Omega \;:\; r_{\omega} \mid r\}$
and let
$\Omega_r \;:\!=\; \{\omega \in \Omega \;:\; r_{\omega} \mid r\}$
and let
![]() $\mu_r \;:\!=\; \int_{\Omega_r}{\mu_{\omega}\;d\rho(\omega)}$
. Then let
$\mu_r \;:\!=\; \int_{\Omega_r}{\mu_{\omega}\;d\rho(\omega)}$
. Then let
![]() $r \in \mathcal{O}_K$
so that
$r \in \mathcal{O}_K$
so that
![]() $\rho(\Omega \setminus \Omega_r) < {\varepsilon}/{2}$
.
$\rho(\Omega \setminus \Omega_r) < {\varepsilon}/{2}$
.
Note that in the proof of the ergodic case, the numbers
![]() $\xi$
and D depend only on r and not on
$\xi$
and D depend only on r and not on
![]() $\mu$
. Thus, for every
$\mu$
. Thus, for every
![]() $\omega \in \Omega_r$
, we have
$\omega \in \Omega_r$
, we have
Now we integrate over
![]() $\Omega$
:
$\Omega$
:
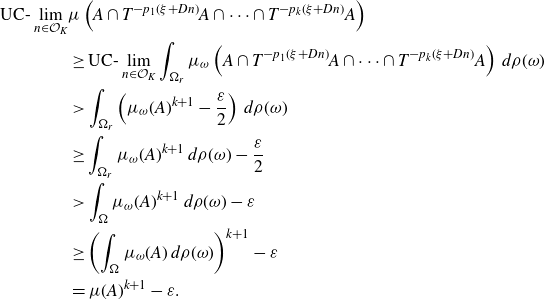 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}&{\mu \left( A \cap T^{-p_1(\xi + Dn)}A \cap \cdots \cap T^{-p_k(\xi + Dn)}A \right)} \\ & \ge \text{UC-}\lim_{n \in \mathcal{O}_K}{\int_{\Omega_r}{ \mu_{\omega} \left( A \cap T^{-p_1(\xi + Dn)}A \cap \cdots \cap T^{-p_k(\xi + Dn)}A \right)\;d\rho(\omega)}} \\ & > \int_{\Omega_r}{\left( \mu_{\omega}(A)^{k+1} - \frac{\varepsilon}{2} \right)\;d\rho(\omega)} \\ & \ge \int_{\Omega_r}{\mu_{\omega}(A)^{k+1}\;d\rho(\omega)} - \frac{\varepsilon}{2} \\ & > \int_{\Omega}{\mu_{\omega}(A)^{k+1}\;d\rho(\omega)} - \varepsilon \\ & \ge \left( \int_{\Omega}{\mu_{\omega}(A)\;d\rho(\omega)} \right)^{k+1} - \varepsilon \\ & = \mu(A)^{k+1} - \varepsilon. \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}&{\mu \left( A \cap T^{-p_1(\xi + Dn)}A \cap \cdots \cap T^{-p_k(\xi + Dn)}A \right)} \\ & \ge \text{UC-}\lim_{n \in \mathcal{O}_K}{\int_{\Omega_r}{ \mu_{\omega} \left( A \cap T^{-p_1(\xi + Dn)}A \cap \cdots \cap T^{-p_k(\xi + Dn)}A \right)\;d\rho(\omega)}} \\ & > \int_{\Omega_r}{\left( \mu_{\omega}(A)^{k+1} - \frac{\varepsilon}{2} \right)\;d\rho(\omega)} \\ & \ge \int_{\Omega_r}{\mu_{\omega}(A)^{k+1}\;d\rho(\omega)} - \frac{\varepsilon}{2} \\ & > \int_{\Omega}{\mu_{\omega}(A)^{k+1}\;d\rho(\omega)} - \varepsilon \\ & \ge \left( \int_{\Omega}{\mu_{\omega}(A)\;d\rho(\omega)} \right)^{k+1} - \varepsilon \\ & = \mu(A)^{k+1} - \varepsilon. \end{align*}
4·2. Proof of Theorem B
Now we turn to proving Theorem B, restated below:
Theorem B.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $p(x) \in K[x]$
be an
$p(x) \in K[x]$
be an
![]() $\mathcal{O}_K$
-valued intersective polynomial. Let
$\mathcal{O}_K$
-valued intersective polynomial. Let
![]() $r,s \in \mathcal{O}_K$
be distinct and nonzero. Then for any ergodic measure-preserving
$r,s \in \mathcal{O}_K$
be distinct and nonzero. Then for any ergodic measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
,
$\left( X, \mathcal{B}, \mu, T \right)$
,
![]() $A \in \mathcal{B}$
, and
$A \in \mathcal{B}$
, and
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is syndetic.
Moreover, if
![]() ${s}/{r} \in \mathbb{Q}$
, then
${s}/{r} \in \mathbb{Q}$
, then
is syndetic.
First we will prove the special case when T is totally ergodic. In this case, by applying Theorem D, we can compute limits explicitly:
Theorem 4·2.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\textbf{X} = (X, \mathcal{B}, \mu, T)$
be a totally ergodic
$\textbf{X} = (X, \mathcal{B}, \mu, T)$
be a totally ergodic
![]() $\mathcal{O}_K$
-system. Let Z be a compact abelian group and
$\mathcal{O}_K$
-system. Let Z be a compact abelian group and
![]() $\alpha \;:\; (\mathcal{O}_K, +) \to Z$
a homomorphism such that the Kronecker factor of
$\alpha \;:\; (\mathcal{O}_K, +) \to Z$
a homomorphism such that the Kronecker factor of
![]() $\textbf{X}$
is isomorphic to the system
$\textbf{X}$
is isomorphic to the system
![]() $\mathbf{Z} = (Z, \mathcal{B}_Z, \mu_Z, S)$
, where
$\mathbf{Z} = (Z, \mathcal{B}_Z, \mu_Z, S)$
, where
![]() $\mathcal{B}_Z$
is the Borel
$\mathcal{B}_Z$
is the Borel
![]() $\sigma$
-algebra,
$\sigma$
-algebra,
![]() $\mu_Z$
is the Haar probability measure, and S acts by rotations
$\mu_Z$
is the Haar probability measure, and S acts by rotations
![]() $S^nz = z + \alpha_n$
for
$S^nz = z + \alpha_n$
for
![]() $n \in \mathcal{O}_K$
.
$n \in \mathcal{O}_K$
.
-
(1) Let
 $r, s \in \mathcal{O}_K$
distinct and nonzero,
$r, s \in \mathcal{O}_K$
distinct and nonzero,
 $p(x) \in K[x]$
an
$p(x) \in K[x]$
an
 $\mathcal{O}_K$
-valued polynomial, and
$\mathcal{O}_K$
-valued polynomial, and
 $f_1, f_2 \in L^{\infty}(\mu)$
. Then (4·1)in
$f_1, f_2 \in L^{\infty}(\mu)$
. Then (4·1)in \begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{T^{rp(n)}f_1(x) \cdot T^{sp(n)}f_2(x)} = \int_{Z^2}{\widetilde{f_1}(z+u) \widetilde{f_2}(z+v)\;d\nu(u,v)} \end{align}
\begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{T^{rp(n)}f_1(x) \cdot T^{sp(n)}f_2(x)} = \int_{Z^2}{\widetilde{f_1}(z+u) \widetilde{f_2}(z+v)\;d\nu(u,v)} \end{align}
 $L^2(\mu)$
, where
$L^2(\mu)$
, where
 $x \mapsto z$
is the factor map,
$x \mapsto z$
is the factor map,
 $\widetilde{f} = \mathbb{E}\left[ {f} \mid {Z} \right]$
, and
$\widetilde{f} = \mathbb{E}\left[ {f} \mid {Z} \right]$
, and
 $\nu$
is the Haar measure on the subgroup
$\nu$
is the Haar measure on the subgroup
 $\overline{\left\{ \left( \alpha_{rn}, \alpha_{sn} \right) \;:\; n \in \mathcal{O}_K \right\}} \subseteq Z^2$
.
$\overline{\left\{ \left( \alpha_{rn}, \alpha_{sn} \right) \;:\; n \in \mathcal{O}_K \right\}} \subseteq Z^2$
.
-
(2) Let
 $a_1, a_2 \in \mathbb{Z} \setminus \{0\}$
be coprime, and put
$a_1, a_2 \in \mathbb{Z} \setminus \{0\}$
be coprime, and put
 $a_3 = a_1 + a_2$
. There is a compact abelian group H such that the nilfactor
$a_3 = a_1 + a_2$
. There is a compact abelian group H such that the nilfactor
 $(X, \mathcal{Z}_2, \mu, T)$
is isomorphic to a skew-product system
$(X, \mathcal{Z}_2, \mu, T)$
is isomorphic to a skew-product system
 $\mathbf{Z} \times_{\sigma} H$
, and there exists a function
$\mathbf{Z} \times_{\sigma} H$
, and there exists a function
 $\psi \;:\; Z^2 \to H$
such that
$\psi \;:\; Z^2 \to H$
such that
 $\psi(0,\cdot) = 0$
and
$\psi(0,\cdot) = 0$
and
 $t \mapsto \psi(t, \cdot)$
is continuous as a function from Z to the space
$t \mapsto \psi(t, \cdot)$
is continuous as a function from Z to the space
 $\mathcal{M}(Z,H)$
of measurable functions
$\mathcal{M}(Z,H)$
of measurable functions
 $Z \to H$
in the topology of convergence in measure, and integers
$Z \to H$
in the topology of convergence in measure, and integers
 $b_1, b_2, b_3 \in \mathbb{Z}$
such that: for any
$b_1, b_2, b_3 \in \mathbb{Z}$
such that: for any
 $\mathcal{O}_K$
-valued polynomial
$\mathcal{O}_K$
-valued polynomial
 $p(x) \in K[x]$
and any
$p(x) \in K[x]$
and any
 $f_1, f_2, f_3 \in L^{\infty}(\mu)$
, we have (4·2)in
$f_1, f_2, f_3 \in L^{\infty}(\mu)$
, we have (4·2)in \begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^3{T^{a_ip(n)}f_i(x)}} = \int_{Z \times H^2}{ \prod_{i=1}^3{\widetilde{f}_i(z + a_it, h + a_iu + a_i^2v + b_i \psi(t,z))}\;dt\;du\;dv} \end{align}
\begin{align} \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^3{T^{a_ip(n)}f_i(x)}} = \int_{Z \times H^2}{ \prod_{i=1}^3{\widetilde{f}_i(z + a_it, h + a_iu + a_i^2v + b_i \psi(t,z))}\;dt\;du\;dv} \end{align}
 $L^2(\mu)$
, where
$L^2(\mu)$
, where
 $\widetilde{f} = \mathbb{E}\left[ {f} \mid {\mathcal{Z}_2} \right]$
.
$\widetilde{f} = \mathbb{E}\left[ {f} \mid {\mathcal{Z}_2} \right]$
.
Proof. Since the system
![]() $\textbf{X}$
is totally ergodic, the limits
$\textbf{X}$
is totally ergodic, the limits
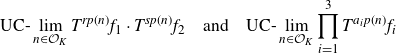 \begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{T^{rp(n)}f_1 \cdot T^{sp(n)}f_2} \quad \text{and} \quad \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^3{T^{a_ip(n)}f_i}} \end{align*}
\begin{align*} \text{UC-}\lim_{n \in \mathcal{O}_K}{T^{rp(n)}f_1 \cdot T^{sp(n)}f_2} \quad \text{and} \quad \text{UC-}\lim_{n \in \mathcal{O}_K}{\prod_{i=1}^3{T^{a_ip(n)}f_i}} \end{align*}
are independent of the choice of the polynomial p by Theorem D. Thus, we may assume without loss of generality that
![]() $p(n) = n$
. The identity (4·1) is then a special case of [
Reference Ackelsberg, Bergelson and Best2
, theorem 3·1], and (4·2) is a special case of [
Reference Ackelsberg, Bergelson and Best2
, theorem 7·1].
$p(n) = n$
. The identity (4·1) is then a special case of [
Reference Ackelsberg, Bergelson and Best2
, theorem 3·1], and (4·2) is a special case of [
Reference Ackelsberg, Bergelson and Best2
, theorem 7·1].
Corollary 4·3.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\textbf{X} = (X, \mathcal{B}, \mu, T)$
be a totally ergodic
$\textbf{X} = (X, \mathcal{B}, \mu, T)$
be a totally ergodic
![]() $\mathcal{O}_K$
-system with Kronecker factor
$\mathcal{O}_K$
-system with Kronecker factor
![]() $(\mathbf{Z}, \alpha)$
.
$(\mathbf{Z}, \alpha)$
.
-
(1) Let
 $r, s \in \mathcal{O}_K$
distinct and nonzero,
$r, s \in \mathcal{O}_K$
distinct and nonzero,
 $p(x) \in K[x]$
an
$p(x) \in K[x]$
an
 $\mathcal{O}_K$
-valued polynomial, and
$\mathcal{O}_K$
-valued polynomial, and
 $f_0, f_1, f_2 \in L^{\infty}(\mu)$
. Then for any continuous function
$f_0, f_1, f_2 \in L^{\infty}(\mu)$
. Then for any continuous function
 $\eta \;:\; Z^2 \to \mathbb{C}$
, we have (4·3)in
$\eta \;:\; Z^2 \to \mathbb{C}$
, we have (4·3)in \begin{align} \begin{split} \text{UC-}\lim_{n \in \mathcal{O}_K}&{\eta \left( \alpha_{rp(n)}, \alpha_{sp(n)} \right) \int_X{f_0 \cdot T^{rp(n)}f_1 \cdot T^{sp(n)}f_2\;d\mu}} \\ & = \int_{Z^3}{\eta(u,v) \widetilde{f_0}(z) \widetilde{f_1}(z+u) \widetilde{f_2}(z+v)\;dz\;d\nu(u,v)} \end{split} \end{align}
\begin{align} \begin{split} \text{UC-}\lim_{n \in \mathcal{O}_K}&{\eta \left( \alpha_{rp(n)}, \alpha_{sp(n)} \right) \int_X{f_0 \cdot T^{rp(n)}f_1 \cdot T^{sp(n)}f_2\;d\mu}} \\ & = \int_{Z^3}{\eta(u,v) \widetilde{f_0}(z) \widetilde{f_1}(z+u) \widetilde{f_2}(z+v)\;dz\;d\nu(u,v)} \end{split} \end{align}
 $L^2(\mu)$
, where
$L^2(\mu)$
, where
 $x \mapsto z$
is the factor map,
$x \mapsto z$
is the factor map,
 $\widetilde{f} = \mathbb{E}\left[ {f} \mid {Z} \right]$
, and
$\widetilde{f} = \mathbb{E}\left[ {f} \mid {Z} \right]$
, and
 $\nu$
is the Haar measure on the subgroup
$\nu$
is the Haar measure on the subgroup
 $\overline{\left\{ \left( \alpha_{rn}, \alpha_{sn} \right) \;:\; n \in \mathcal{O}_K \right\}} \subseteq Z^2$
.
$\overline{\left\{ \left( \alpha_{rn}, \alpha_{sn} \right) \;:\; n \in \mathcal{O}_K \right\}} \subseteq Z^2$
.
-
(2) Let
 $a_1, a_2 \in \mathbb{Z} \setminus \{0\}$
be coprime, and put
$a_1, a_2 \in \mathbb{Z} \setminus \{0\}$
be coprime, and put
 $a_0 = 0, a_3 = a_1 + a_2$
. Let H,
$a_0 = 0, a_3 = a_1 + a_2$
. Let H,
 $\psi$
, and
$\psi$
, and
 $b_i$
be as in Theorem 4·2(2). Let
$b_i$
be as in Theorem 4·2(2). Let
 $p(x) \in K[x]$
be an
$p(x) \in K[x]$
be an
 $\mathcal{O}_K$
-valued polynomial, and let
$\mathcal{O}_K$
-valued polynomial, and let
 $f_0, f_1, f_2, f_3 \in L^{\infty}(\mu)$
. Then for any continuous function
$f_0, f_1, f_2, f_3 \in L^{\infty}(\mu)$
. Then for any continuous function
 $\eta \;:\; Z \to \mathbb{C}$
, (4·4)in
$\eta \;:\; Z \to \mathbb{C}$
, (4·4)in \begin{align} \begin{split} \text{UC-}\lim_{n \in \mathcal{O}_K}&{\eta \left( \alpha_{p(n)} \right) \int_X{\prod_{i=0}^3{T^{a_ip(n)}f_i}\;d\mu}} \\ & = \int_{Z^2 \times H^3}{\eta(t) \prod_{i=0}^3{\widetilde{f}_i(z + a_it, h + a_iu + a_i^2v + b_i \psi(t,z))}\;dz\;dt\;dh\;du\;dv} \end{split} \end{align}
\begin{align} \begin{split} \text{UC-}\lim_{n \in \mathcal{O}_K}&{\eta \left( \alpha_{p(n)} \right) \int_X{\prod_{i=0}^3{T^{a_ip(n)}f_i}\;d\mu}} \\ & = \int_{Z^2 \times H^3}{\eta(t) \prod_{i=0}^3{\widetilde{f}_i(z + a_it, h + a_iu + a_i^2v + b_i \psi(t,z))}\;dz\;dt\;dh\;du\;dv} \end{split} \end{align}
 $L^2(\mu)$
, where
$L^2(\mu)$
, where
 $\widetilde{f} = \mathbb{E}\left[ {f} \mid {\mathcal{Z}_2} \right]$
.
$\widetilde{f} = \mathbb{E}\left[ {f} \mid {\mathcal{Z}_2} \right]$
.
Proof.
-
(1) Since
 $Z^2$
is a compact abelian group, we may assume by the Stone–Weierstrass theorem that
$Z^2$
is a compact abelian group, we may assume by the Stone–Weierstrass theorem that
 $\eta(u,v) = \lambda_1(u)\lambda_2(v)$
for
$\eta(u,v) = \lambda_1(u)\lambda_2(v)$
for
 $u, v \in Z$
, where
$u, v \in Z$
, where
 $\lambda_1, \lambda_2 \in \widehat{Z}$
. Defining for
$\lambda_1, \lambda_2 \in \widehat{Z}$
. Defining for
 $i = 1, 2$
, the formula (4·3) then follows by applying (4·1) to the functions
$i = 1, 2$
, the formula (4·3) then follows by applying (4·1) to the functions
 $g_1, g_2$
and integrating against
$g_1, g_2$
and integrating against
 $g_0$
.
$g_0$
.
-
(2) Again, without loss of generality, we may assume
 $\eta = \lambda \in \widehat{Z}$
. Since
$\eta = \lambda \in \widehat{Z}$
. Since
 $\gcd(a_1, a_2) = 1$
, there are integers
$\gcd(a_1, a_2) = 1$
, there are integers
 $c_1, c_2 \in \mathbb{Z}$
so that
$c_1, c_2 \in \mathbb{Z}$
so that
 $c_1a_1 + c_2a_2 = 1$
. Let
$c_1a_1 + c_2a_2 = 1$
. Let
 $c_3 = 0$
and
$c_3 = 0$
and
 $c_0 = -(c_1+c_2)$
so that Then define
$c_0 = -(c_1+c_2)$
so that Then define \begin{align*} \sum_{i=0}^3{c_i} = 0 \quad \text{and} \quad \sum_{i=0}^3{c_ia_i} = 1. \end{align*}
\begin{align*} \sum_{i=0}^3{c_i} = 0 \quad \text{and} \quad \sum_{i=0}^3{c_ia_i} = 1. \end{align*}
 $g_i(x) \;:\!=\; \lambda(c_iz) f_i(x)$
for
$g_i(x) \;:\!=\; \lambda(c_iz) f_i(x)$
for
 $i = 0, 1, 2, 3$
. Applying the formula (4·2) for the functions
$i = 0, 1, 2, 3$
. Applying the formula (4·2) for the functions
 $g_1, g_2, g_3$
and integrating against
$g_1, g_2, g_3$
and integrating against
 $g_0$
produces the desired formula (4·1).
$g_0$
produces the desired formula (4·1).
Proposition 4·4.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $(X, \mathcal{B}, \mu, T)$
be a totally ergodic
$(X, \mathcal{B}, \mu, T)$
be a totally ergodic
![]() $\mathcal{O}_K$
-system,
$\mathcal{O}_K$
-system,
![]() $r, s \in \mathcal{O}_K$
distinct and nonzero, and
$r, s \in \mathcal{O}_K$
distinct and nonzero, and
![]() $p(x) \in K[x]$
an
$p(x) \in K[x]$
an
![]() $\mathcal{O}_K$
-valued polynomial. Then for any
$\mathcal{O}_K$
-valued polynomial. Then for any
![]() $A \in \mathcal{B}$
with
$A \in \mathcal{B}$
with
![]() $\mu(A) > 0$
and any
$\mu(A) > 0$
and any
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is syndetic.
Moreover, if
![]() ${s}/{r} \in \mathbb{Q}$
, then
${s}/{r} \in \mathbb{Q}$
, then
is syndetic.
Remark 4·5. We do not assume that the polynomial p is intersective in Proposition 4·4. This is because, in the totally ergodic setting, there are no “local obstructions” that need to be avoided. In order to extend to the ergodic setting, however, we will have to restrict to intersective polynomials.
Proof of Proposition 4·4. We adapt the method from [ Reference Frantzikinakis19 ].
First we prove the double recurrence result. Using the formula (4·3) with
![]() $f_i = \mathbb{1}_A$
and choosing
$f_i = \mathbb{1}_A$
and choosing
![]() $\eta$
supported on a small neighborhood of 0, it suffices to show
$\eta$
supported on a small neighborhood of 0, it suffices to show
But this follows immediately from Jensen’s inequality, so
is syndetic.
Now we move to triple recurrence. Since
![]() $\frac{s}{r} \in \mathbb{Q}$
, we can write
$\frac{s}{r} \in \mathbb{Q}$
, we can write
![]() $r = a_1k$
and
$r = a_1k$
and
![]() $s = a_2k$
for some coprime
$s = a_2k$
for some coprime
![]() $a_1, a_2 \in \mathbb{Z}$
and some
$a_1, a_2 \in \mathbb{Z}$
and some
![]() $k \in K$
. Let
$k \in K$
. Let
![]() $q(n) = kp(n)$
. Note that
$q(n) = kp(n)$
. Note that
![]() $a_1q(n) = rp(n)$
and
$a_1q(n) = rp(n)$
and
![]() $a_2q(n) = sp(n)$
are
$a_2q(n) = sp(n)$
are
![]() $\mathcal{O}_K$
-valued. Therefore, q is itself
$\mathcal{O}_K$
-valued. Therefore, q is itself
![]() $\mathcal{O}_K$
-valued, since
$\mathcal{O}_K$
-valued, since
![]() $\gcd(a_1, a_2) = 1$
. Hence, without loss of generality, we will assume that r and s are coprime integers.
$\gcd(a_1, a_2) = 1$
. Hence, without loss of generality, we will assume that r and s are coprime integers.
Now put
![]() $a_0 = 0$
,
$a_0 = 0$
,
![]() $a_1 = r$
,
$a_1 = r$
,
![]() $a_2 = s$
, and
$a_2 = s$
, and
![]() $a_3 = r + s$
. Applying formula (4·4) with
$a_3 = r + s$
. Applying formula (4·4) with
![]() $f_i = \mathbb{1}_A$
and choosing the function
$f_i = \mathbb{1}_A$
and choosing the function
![]() $\eta$
to be supported on a small neighbourhood of 0, we want to show
$\eta$
to be supported on a small neighbourhood of 0, we want to show
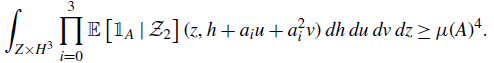 \begin{align} \int_{Z \times H^3}{\prod_{i=0}^3{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{Z}_2} \right](z, h + a_iu + a_i^2v)}\;dh\;du\;dv\;dz} \ge \mu(A)^4. \end{align}
\begin{align} \int_{Z \times H^3}{\prod_{i=0}^3{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{Z}_2} \right](z, h + a_iu + a_i^2v)}\;dh\;du\;dv\;dz} \ge \mu(A)^4. \end{align}
Fix
![]() $z \in Z$
, and let
$z \in Z$
, and let
![]() $F_z \;:\; H \to [0,1]$
be the function
$F_z \;:\; H \to [0,1]$
be the function
![]() $F_z(x) = \mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{Z}_2} \right](z,x)$
. Now we perform several changes of variables. First, take
$F_z(x) = \mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{Z}_2} \right](z,x)$
. Now we perform several changes of variables. First, take
![]() $h = a_3x$
:
$h = a_3x$
:
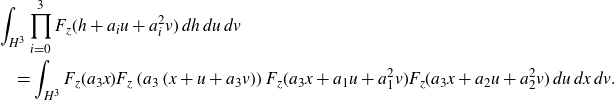 \begin{align*} & \int_{H^3}{\prod_{i=0}^3{F_z(h + a_iu + a_i^2v)}\;dh\;du\;dv} \\ & \quad = \int_{H^3}{F_z(a_3x) F_z\left( a_3\left( x + u + a_3v \right) \right) F_z(a_3x + a_1u + a_1^2v) F_z(a_3x + a_2u + a_2^2v)\;du\;dx\;dv}. \end{align*}
\begin{align*} & \int_{H^3}{\prod_{i=0}^3{F_z(h + a_iu + a_i^2v)}\;dh\;du\;dv} \\ & \quad = \int_{H^3}{F_z(a_3x) F_z\left( a_3\left( x + u + a_3v \right) \right) F_z(a_3x + a_1u + a_1^2v) F_z(a_3x + a_2u + a_2^2v)\;du\;dx\;dv}. \end{align*}
Next,
![]() $x + u + a_3v = y$
:
$x + u + a_3v = y$
:
Now,
![]() $a_1(x+y) - a_1a_2v = w$
:
$a_1(x+y) - a_1a_2v = w$
:
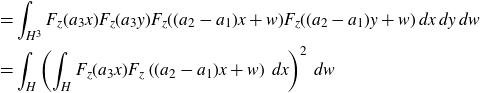 \begin{align*} &= \int_{H^3}{F_z(a_3x) F_z(a_3y) F_z((a_2-a_1)x + w) F_z((a_2-a_1)y + w)\;dx\;dy\;dw} \\ & = \int_H{\left( \int_H{F_z(a_3x) F_z \left( (a_2 - a_1)x + w \right)\;dx}\right)^2\;dw} \end{align*}
\begin{align*} &= \int_{H^3}{F_z(a_3x) F_z(a_3y) F_z((a_2-a_1)x + w) F_z((a_2-a_1)y + w)\;dx\;dy\;dw} \\ & = \int_H{\left( \int_H{F_z(a_3x) F_z \left( (a_2 - a_1)x + w \right)\;dx}\right)^2\;dw} \end{align*}
Apply Jensen's inequality:
Finally, let
![]() $w + (a_2-a_1)x = u\; \textrm{and}\; a_3x = t$
:
$w + (a_2-a_1)x = u\; \textrm{and}\; a_3x = t$
:
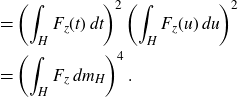 \begin{align*} & = \left( \int_H{F_z(t)\;dt} \right)^2 \left( \int_H{F_z(u)\;du} \right)^2 \\ & = \left( \int_H{F_z\;dm_H} \right)^4. \end{align*}
\begin{align*} & = \left( \int_H{F_z(t)\;dt} \right)^2 \left( \int_H{F_z(u)\;du} \right)^2 \\ & = \left( \int_H{F_z\;dm_H} \right)^4. \end{align*}
Thus, applying Jensen’s inequality one more time, we have
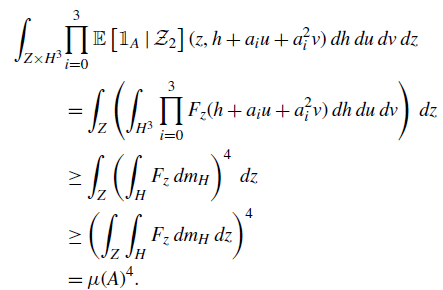 \begin{align*} \int_{Z \times H^3}&{\prod_{i=0}^3{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{Z}_2} \right](z, h + a_iu + a_i^2v)}\;dh\;du\;dv\;dz} \\ &= \int_Z{\left( \int_{H^3}{\prod_{i=0}^3{F_z(h + a_iu + a_i^2v)}\;dh\;du\;dv} \right)\;dz} \\ & \ge \int_Z{ \left( \int_H{F_z\;dm_H} \right)^4\;dz} \\ & \ge \left( \int_Z{\int_H{F_z\;dm_H}\;dz} \right)^4 \\ & = \mu(A)^4. \end{align*}
\begin{align*} \int_{Z \times H^3}&{\prod_{i=0}^3{\mathbb{E}\left[ {\mathbb{1}_A} \mid {\mathcal{Z}_2} \right](z, h + a_iu + a_i^2v)}\;dh\;du\;dv\;dz} \\ &= \int_Z{\left( \int_{H^3}{\prod_{i=0}^3{F_z(h + a_iu + a_i^2v)}\;dh\;du\;dv} \right)\;dz} \\ & \ge \int_Z{ \left( \int_H{F_z\;dm_H} \right)^4\;dz} \\ & \ge \left( \int_Z{\int_H{F_z\;dm_H}\;dz} \right)^4 \\ & = \mu(A)^4. \end{align*}
That is, the inequality (4·5) holds, so the set
is syndetic.
We have proved Theorem B in the case when T is totally ergodic. We will now extend this to the general case that T is simply ergodic. Theorem D still applies, so by a standard approximation argument, we may assume without loss of generality that T acts by niltranslations. The Kronecker factor is then a group of the form
![]() $\mathbb{Z}_{a_1} \times \cdots \times \mathbb{Z}_{a_d} \times \mathbb{T}^{c}$
. As in the proof of Proposition 2·13, we can therefore find
$\mathbb{Z}_{a_1} \times \cdots \times \mathbb{Z}_{a_d} \times \mathbb{T}^{c}$
. As in the proof of Proposition 2·13, we can therefore find
![]() $k \in \mathcal{O}_K$
such that the Kronecker factor of
$k \in \mathcal{O}_K$
such that the Kronecker factor of
![]() $\left( T^{kn} \right)_{n \in \mathcal{O}_K}$
is connected, and hence each of the finitely many ergodic components of
$\left( T^{kn} \right)_{n \in \mathcal{O}_K}$
is connected, and hence each of the finitely many ergodic components of
![]() $\left( T^{kn} \right)_{n \in \mathcal{O}_K}$
is totally ergodic by Proposition 2·4. Let
$\left( T^{kn} \right)_{n \in \mathcal{O}_K}$
is totally ergodic by Proposition 2·4. Let
![]() $X_1, \dots, X_m$
the atoms of the
$X_1, \dots, X_m$
the atoms of the
![]() $\left( T^{kn} \right)_{n \in \mathcal{O}_K}$
-invariant
$\left( T^{kn} \right)_{n \in \mathcal{O}_K}$
-invariant
![]() $\sigma$
-algebra, and let
$\sigma$
-algebra, and let
![]() $\mu_j(B) \;:\!=\; m \cdot \mu(B \cap X_j)$
so that
$\mu_j(B) \;:\!=\; m \cdot \mu(B \cap X_j)$
so that
![]() $\mu$
has ergodic decomposition
$\mu$
has ergodic decomposition
![]() $\mu = ({1}/{m}) \sum_{j=1}^m{\mu_j}$
for the action
$\mu = ({1}/{m}) \sum_{j=1}^m{\mu_j}$
for the action
![]() $(T^{kn})_{n \in \mathcal{O}_K}$
.
$(T^{kn})_{n \in \mathcal{O}_K}$
.
By Lemma 2·11, let
![]() $\xi \in \mathcal{O}_K$
and
$\xi \in \mathcal{O}_K$
and
![]() $D \in \mathcal{O}_K \setminus \{0\}$
so that
$D \in \mathcal{O}_K \setminus \{0\}$
so that
![]() $p(\xi + D\mathcal{O}_K) \subseteq k\mathcal{O}_K$
. Let
$p(\xi + D\mathcal{O}_K) \subseteq k\mathcal{O}_K$
. Let
![]() $q(x) \in K[x]$
be the
$q(x) \in K[x]$
be the
![]() $\mathcal{O}_K$
-valued polynomial
$\mathcal{O}_K$
-valued polynomial
![]() $q(n) = k^{-1}p(\xi + Dn)$
for every
$q(n) = k^{-1}p(\xi + Dn)$
for every
![]() $n \in \mathcal{O}_K$
. Following the argument in the proof of Proposition 4·4, we can choose a continuous function
$n \in \mathcal{O}_K$
. Following the argument in the proof of Proposition 4·4, we can choose a continuous function
![]() $\eta$
concentrated on a sufficiently small neighborhood of 0 in
$\eta$
concentrated on a sufficiently small neighborhood of 0 in
![]() $Z^2$
with
$Z^2$
with
![]() $\int_{Z^2}{\eta\;d\nu} = 1$
so that
$\int_{Z^2}{\eta\;d\nu} = 1$
so that
for
![]() $j = 1, \dots, m$
. Summing over
$j = 1, \dots, m$
. Summing over
![]() $j = 1, \dots, m$
and applying Jensen’s inequality, we get
$j = 1, \dots, m$
and applying Jensen’s inequality, we get
from which it follows that
is syndetic in
![]() $\mathcal{O}_K$
.
$\mathcal{O}_K$
.
A similar argument with the ergodic decomposition can be used to show that, if
![]() $\frac{s}{r} \in \mathbb{Q}$
, then
$\frac{s}{r} \in \mathbb{Q}$
, then
is also syndetic.
Thus, the sets
and (if
![]() ${s}/{r} \in \mathbb{Q}$
)
${s}/{r} \in \mathbb{Q}$
)
are relatively syndetic in
![]() $\xi + D\mathcal{O}_K$
. But
$\xi + D\mathcal{O}_K$
. But
![]() $\xi + D\mathcal{O}_K$
is syndetic in
$\xi + D\mathcal{O}_K$
is syndetic in
![]() $\mathcal{O}_K$
, so we are done.
$\mathcal{O}_K$
, so we are done.
5. Refinements
5·1. Polynomial IP sets
Recall that a set
![]() $E \subseteq \mathcal{O}_K$
is
$E \subseteq \mathcal{O}_K$
is
![]() $\text{IP}^*$
if it intersects every finite sum set
$\text{IP}^*$
if it intersects every finite sum set
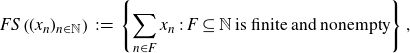 \begin{align*} FS \left( (x_n)_{n \in \mathbb{N}} \right) \;:\!=\; \left\{ \sum_{n \in F}{x_n} \;:\; F \subseteq \mathbb{N}\;\text{is finite and nonempty} \right\},\end{align*}
\begin{align*} FS \left( (x_n)_{n \in \mathbb{N}} \right) \;:\!=\; \left\{ \sum_{n \in F}{x_n} \;:\; F \subseteq \mathbb{N}\;\text{is finite and nonempty} \right\},\end{align*}
where
![]() $(x_n)_{n \in \mathbb{N}}$
is a sequence of distinct elements of
$(x_n)_{n \in \mathbb{N}}$
is a sequence of distinct elements of
![]() $\mathcal{O}_K$
. Similarly, we say E is
$\mathcal{O}_K$
. Similarly, we say E is
![]() $\text{IP}_r^*$
if it intersects every finite sum set of the form
$\text{IP}_r^*$
if it intersects every finite sum set of the form
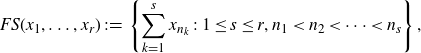 \begin{align*} FS(x_1, \dots, x_r) \;:\!=\; \left\{ \sum_{k=1}^s{x_{n_k}} \;:\; 1 \le s \le r, n_1 < n_2 < \dots < n_s \right\},\end{align*}
\begin{align*} FS(x_1, \dots, x_r) \;:\!=\; \left\{ \sum_{k=1}^s{x_{n_k}} \;:\; 1 \le s \le r, n_1 < n_2 < \dots < n_s \right\},\end{align*}
where
![]() $x_1, \dots, x_r \in \mathcal{O}_K$
are distinct and nonzero. Finally, E is called an
$x_1, \dots, x_r \in \mathcal{O}_K$
are distinct and nonzero. Finally, E is called an
![]() $\text{IP}_0^*$
set if E is
$\text{IP}_0^*$
set if E is
![]() $\text{IP}_r^*$
for some
$\text{IP}_r^*$
for some
![]() $r \in \mathbb{N}$
. Clearly, every
$r \in \mathbb{N}$
. Clearly, every
![]() $\text{IP}_0^*$
set is also
$\text{IP}_0^*$
set is also
![]() $\text{IP}^*$
, but the converse is not true.
$\text{IP}^*$
, but the converse is not true.
Now we will define polynomial generalisations of IP and
![]() $\text{IP}_0$
sets. For a set S, let
$\text{IP}_0$
sets. For a set S, let
![]() $\mathcal{F}(S)$
denote the semigroup of finite subsets of S with the union operation.
$\mathcal{F}(S)$
denote the semigroup of finite subsets of S with the union operation.
Definition 5·1. Let
![]() $(H,+)$
be an abelian group, and let
$(H,+)$
be an abelian group, and let
![]() $\varphi \;:\; \mathcal{F}(S) \to H$
.
$\varphi \;:\; \mathcal{F}(S) \to H$
.
-
(1) We say that
 $\varphi$
is linear if
$\varphi$
is linear if
 $\varphi(\alpha \cup \beta) = \varphi(\alpha) + \varphi(\beta)$
whenever
$\varphi(\alpha \cup \beta) = \varphi(\alpha) + \varphi(\beta)$
whenever
 $\alpha \cap \beta = \emptyset$
.
$\alpha \cap \beta = \emptyset$
. -
(2) For
 $\beta \in \mathcal{F}(S)$
, the
$\beta \in \mathcal{F}(S)$
, the
 $\beta$
-derivate of
$\beta$
-derivate of
 $\varphi$
is the function
$\varphi$
is the function
 $D_{\beta}\varphi \;:\; \mathcal{F}(S \setminus \beta) \to H$
given by
$D_{\beta}\varphi \;:\; \mathcal{F}(S \setminus \beta) \to H$
given by
 $D_{\beta}\varphi(\alpha) = \varphi(\alpha \cup \beta) - \varphi(\alpha)$
.
$D_{\beta}\varphi(\alpha) = \varphi(\alpha \cup \beta) - \varphi(\alpha)$
. -
(3) We say
 $\varphi$
is a polynomial of degree
$\varphi$
is a polynomial of degree
 $\le d$
if for any disjoint sets
$\le d$
if for any disjoint sets
 $\beta_0, \dots, \beta_d \in \mathcal{F}(S)$
, one has
$\beta_0, \dots, \beta_d \in \mathcal{F}(S)$
, one has
 $D_{\beta_0} D_{\beta_1} \cdots D_{\beta_d}\varphi = 0$
.
$D_{\beta_0} D_{\beta_1} \cdots D_{\beta_d}\varphi = 0$
.
Note that an IP set has the form
![]() $\{\varphi(\alpha) \;:\; \alpha \in \mathcal{F}(\mathbb{N}), \alpha \ne \emptyset\}$
for a linear mapping
$\{\varphi(\alpha) \;:\; \alpha \in \mathcal{F}(\mathbb{N}), \alpha \ne \emptyset\}$
for a linear mapping
![]() $\varphi \;:\; \mathcal{F}(S) \to \mathcal{O}_K$
with
$\varphi \;:\; \mathcal{F}(S) \to \mathcal{O}_K$
with
![]() $\varphi(\emptyset) = 0$
. For a polynomial mapping
$\varphi(\emptyset) = 0$
. For a polynomial mapping
![]() $\varphi \;:\; \mathcal{F}(S) \to \mathcal{O}_K$
, we call the corresponding set
$\varphi \;:\; \mathcal{F}(S) \to \mathcal{O}_K$
, we call the corresponding set
![]() $\{\varphi(\alpha) \;:\; \alpha \in \mathcal{F}(\mathbb{N}), \alpha \ne \emptyset\}$
a VIP set. Similarly, if
$\{\varphi(\alpha) \;:\; \alpha \in \mathcal{F}(\mathbb{N}), \alpha \ne \emptyset\}$
a VIP set. Similarly, if
![]() $\varphi \;:\; \mathcal{F}(\{1, \dots, r\} \to \mathcal{O}_K$
is a polynomial mapping of degree
$\varphi \;:\; \mathcal{F}(\{1, \dots, r\} \to \mathcal{O}_K$
is a polynomial mapping of degree
![]() $\le d$
with
$\le d$
with
![]() $\varphi(\emptyset) = 0$
, we say that
$\varphi(\emptyset) = 0$
, we say that
![]() $\{\varphi(\alpha) \;:\; \alpha \in \mathcal{F}(\{1, \dots, r\}), \alpha \ne \emptyset\}$
is
$\{\varphi(\alpha) \;:\; \alpha \in \mathcal{F}(\{1, \dots, r\}), \alpha \ne \emptyset\}$
is
![]() $\text{VIP}_{d,r}$
. A set
$\text{VIP}_{d,r}$
. A set
![]() $E \subseteq \mathcal{O}_K$
is
$E \subseteq \mathcal{O}_K$
is
![]() $\text{VIP}^*$
if it intersects every VIP set, and E is
$\text{VIP}^*$
if it intersects every VIP set, and E is
![]() $\text{VIP}_{d,r}^*$
if it intersects every
$\text{VIP}_{d,r}^*$
if it intersects every
![]() $\text{VIP}_{d,r}$
set. Finally, E is
$\text{VIP}_{d,r}$
set. Finally, E is
![]() $\text{VIP}_0^*$
if for any
$\text{VIP}_0^*$
if for any
![]() $d \in \mathbb{N}$
, E is
$d \in \mathbb{N}$
, E is
![]() $\text{VIP}_{d,r}^*$
for some
$\text{VIP}_{d,r}^*$
for some
![]() $r \in \mathbb{N}$
.
$r \in \mathbb{N}$
.
As we will see below,
![]() $\text{VIP}_0^*$
is an appropriate notion of largeness for nilsequences. However, for a multi-correlation sequence, which differs from a nilsequence by a nullsequence (see Theorem 5·4 below), we need the slightly weaker notion of
$\text{VIP}_0^*$
is an appropriate notion of largeness for nilsequences. However, for a multi-correlation sequence, which differs from a nilsequence by a nullsequence (see Theorem 5·4 below), we need the slightly weaker notion of
![]() $\text{AVIP}_0^*$
. A set E is almost-
$\text{AVIP}_0^*$
. A set E is almost-
![]() $\text{VIP}_0^*$
, or
$\text{VIP}_0^*$
, or
![]() $\text{AVIP}_0^*$
for short, if there is a
$\text{AVIP}_0^*$
for short, if there is a
![]() $\text{VIP}_0^*$
set A such that
$\text{VIP}_0^*$
set A such that
![]() $d^*(A \setminus E) = 0$
.
$d^*(A \setminus E) = 0$
.
For any notion of largeness discussed so far, we use the added decoration of
![]() $+$
in the subscript to indicate a shift. In particular,
$+$
in the subscript to indicate a shift. In particular,
![]() $\text{(A)VIP}_{0,+}^*$
means a shift of an
$\text{(A)VIP}_{0,+}^*$
means a shift of an
![]() $\text{(A)VIP}_0^*$
set.
$\text{(A)VIP}_0^*$
set.
5·2. Recurrence in nilmanifolds
Theorem 5·2 ([
Reference Bergelson and Leibman8
, theorem 0·6]). Let (X, T) be a
![]() $\mathbb{Z}^d$
-nilsystem. Then, for any
$\mathbb{Z}^d$
-nilsystem. Then, for any
![]() $x_0 \in X$
and any neighbourhood U of
$x_0 \in X$
and any neighbourhood U of
![]() $x_0$
, the set
$x_0$
, the set
is a
![]() $\text{VIP}_0^*$
set.
$\text{VIP}_0^*$
set.
Corollary 5·3.
Let
![]() $\varphi \;:\; \mathbb{Z}^d \to \mathbb{R}$
be a nilsequence. For any
$\varphi \;:\; \mathbb{Z}^d \to \mathbb{R}$
be a nilsequence. For any
![]() $c < \sup{\varphi}$
, the set
$c < \sup{\varphi}$
, the set
is
![]() $\text{VIP}_{0,+}^*$
.
$\text{VIP}_{0,+}^*$
.
Proof. Let
![]() $\varepsilon = \sup{\varphi} - c > 0$
. Then let (X, T) be a minimal nilsystem,
$\varepsilon = \sup{\varphi} - c > 0$
. Then let (X, T) be a minimal nilsystem,
![]() $x_0 \in X$
, and
$x_0 \in X$
, and
![]() $F \in C(X)$
such that
$F \in C(X)$
such that
![]() $\sup_{n \in \mathbb{Z}^d}{\left| \varphi(n) - F(T^nx_0) \right|} < {\varepsilon}/{2}$
. Note that
$\sup_{n \in \mathbb{Z}^d}{\left| \varphi(n) - F(T^nx_0) \right|} < {\varepsilon}/{2}$
. Note that
![]() $\sup{F} > \sup{\varphi} - {\varepsilon}/{2}$
.
$\sup{F} > \sup{\varphi} - {\varepsilon}/{2}$
.
Let
![]() $U \;:\!=\; \left\{ x \in X \;:\; F(x) > \sup{\varphi} - {\varepsilon}/{2} \right\}$
. Then U is a nonempty open set. Since (X, T) is minimal, we have
$U \;:\!=\; \left\{ x \in X \;:\; F(x) > \sup{\varphi} - {\varepsilon}/{2} \right\}$
. Then U is a nonempty open set. Since (X, T) is minimal, we have
![]() $T^mx_0 \in U$
for some
$T^mx_0 \in U$
for some
![]() $m \in \mathbb{Z}^d$
. By Theorem 5·2,
$m \in \mathbb{Z}^d$
. By Theorem 5·2,
is
![]() $\text{VIP}_0^*$
.
$\text{VIP}_0^*$
.
Suppose
![]() $n \in S$
. Then
$n \in S$
. Then
Therefore,
![]() $R \supseteq S + m$
is
$R \supseteq S + m$
is
![]() $\text{VIP}_{0,+}^*$
.
$\text{VIP}_{0,+}^*$
.
5·3. Nilsequence-nulsequence decomposition
Let
![]() $r \in \mathbb{N}$
. A basic r-step nilsequence is a function
$r \in \mathbb{N}$
. A basic r-step nilsequence is a function
![]() $\varphi(n) = F(T^nx_0)$
, where
$\varphi(n) = F(T^nx_0)$
, where
![]() $(X, \mathcal{B}, \mu, T)$
is an r-step nilsystem,
$(X, \mathcal{B}, \mu, T)$
is an r-step nilsystem,
![]() $F \;:\; X \to \mathbb{C}$
is a continuous function, and
$F \;:\; X \to \mathbb{C}$
is a continuous function, and
![]() $x_0 \in X$
. An r-step nilsequence is a uniform limit of basic r-step nilsequences. Knowing that a nilfactor is characteristic for polynomial multiple ergodic averages gives a decomposition of the corresponding multi-correlation sequences. Recall that a function
$x_0 \in X$
. An r-step nilsequence is a uniform limit of basic r-step nilsequences. Knowing that a nilfactor is characteristic for polynomial multiple ergodic averages gives a decomposition of the corresponding multi-correlation sequences. Recall that a function
![]() $\psi \;:\; \mathcal{O}_K \to \mathbb{C}$
is a nullsequence if
$\psi \;:\; \mathcal{O}_K \to \mathbb{C}$
is a nullsequence if
![]() $\text{UC-}\lim_{n \in \mathcal{O}_K}{|\psi(n)|^2} = 0$
.
$\text{UC-}\lim_{n \in \mathcal{O}_K}{|\psi(n)|^2} = 0$
.
Theorem 5·4.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $p_1, \dots, p_k \in K[x]$
be non-constant, essentially distinct,
$p_1, \dots, p_k \in K[x]$
be non-constant, essentially distinct,
![]() $\mathcal{O}_K$
-valued polynomials. Then for any ergodic measure-preserving
$\mathcal{O}_K$
-valued polynomials. Then for any ergodic measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
and any
$\left( X, \mathcal{B}, \mu, T \right)$
and any
![]() $f_0, f_1, \dots, f_k \in L^{\infty}(\mu)$
, there is a decomposition
$f_0, f_1, \dots, f_k \in L^{\infty}(\mu)$
, there is a decomposition
where
![]() $\varphi$
is a nilsequence and
$\varphi$
is a nilsequence and
![]() $\psi$
is a nullsequence.
$\psi$
is a nullsequence.
Proof. First, by [
Reference Bergelson and Robertson14
, theorem 5·2], there exists
![]() $r \in \mathbb{N}$
such that
$r \in \mathbb{N}$
such that
is a nullsequence, so we may assume that
![]() $(X, \mathcal{B}, \mu, T)$
is a nilsystem.
$(X, \mathcal{B}, \mu, T)$
is a nilsystem.
Next, up to a uniform approximation in n, we may assume that
![]() $f_0, f_1, \dots, f_k$
are continuous functions. Then by [
Reference Leibman36
, theorem 1·3], a(n) is the sum of a (basic) nilsequence and a nullsequence. Taking a uniform limit gives the desired decomposition.
$f_0, f_1, \dots, f_k$
are continuous functions. Then by [
Reference Leibman36
, theorem 1·3], a(n) is the sum of a (basic) nilsequence and a nullsequence. Taking a uniform limit gives the desired decomposition.
Proposition 5·5.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Suppose
$\mathcal{O}_K$
. Suppose
![]() $\varphi \;:\; \mathcal{O}_K \to \mathbb{C}$
is a nilsequence,
$\varphi \;:\; \mathcal{O}_K \to \mathbb{C}$
is a nilsequence,
![]() $\psi \;:\; \mathcal{O}_K \to \mathbb{C}$
is a nullsequence, and
$\psi \;:\; \mathcal{O}_K \to \mathbb{C}$
is a nullsequence, and
![]() $a(n) = \varphi(n) + \psi(n)$
. Suppose that for some
$a(n) = \varphi(n) + \psi(n)$
. Suppose that for some
![]() $c > 0$
, the set
$c > 0$
, the set
is syndetic. Then R(c’) is
![]() $\text{AVIP}_{0,+}^*$
for every
$\text{AVIP}_{0,+}^*$
for every
![]() $c' < c$
.
$c' < c$
.
Proof. Let
![]() $c' < c$
. Then the set
$c' < c$
. Then the set
has upper Banach density
![]() $d^*(E) = 0$
. Therefore,
$d^*(E) = 0$
. Therefore,
![]() $R(c) \setminus E$
is still syndetic; in particular, it is nonempty. But for
$R(c) \setminus E$
is still syndetic; in particular, it is nonempty. But for
![]() $n \in R(c) \setminus E$
, we have
$n \in R(c) \setminus E$
, we have
![]() $\varphi(n) > c - ({c-c'}/{2}) = ({c+c'}/{2})$
. So, by Corollary 5·3,
$\varphi(n) > c - ({c-c'}/{2}) = ({c+c'}/{2})$
. So, by Corollary 5·3,
is
![]() $\text{VIP}_{0,+}^*$
. Finally, since
$\text{VIP}_{0,+}^*$
. Finally, since
![]() $({c+c'})/{2} - ({c-c'})/{2} = c'$
, we have
$({c+c'})/{2} - ({c-c'})/{2} = c'$
, we have
![]() $R(c') \supseteq S \setminus E$
, so R(c’) is
$R(c') \supseteq S \setminus E$
, so R(c’) is
![]() $\text{AVIP}_{0,+}^*$
.
$\text{AVIP}_{0,+}^*$
.
By Theorem 5·4, Proposition 5·5 applies to polynomial multi-correlation sequences in ergodic systems. We can therefore strengthen the conclusions of Theorems 4·1 and 4·2, respectively, under the assumption of ergodicity:
Theorem 5·6.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
$\{p_1, \dots , p_k\} \subseteq K[x]$
be a jointly intersective family of linearly independent
![]() $\mathcal{O}_K$
-valued polynomials. Then for any ergodic measure-preserving
$\mathcal{O}_K$
-valued polynomials. Then for any ergodic measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
,
$\left( X, \mathcal{B}, \mu, T \right)$
,
![]() $A \in \mathcal{B}$
, and
$A \in \mathcal{B}$
, and
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is
![]() $\text{AVIP}_{0,+}^*$
.
$\text{AVIP}_{0,+}^*$
.
Theorem 5·7.
Let K be a number field with ring of integers
![]() $\mathcal{O}_K$
. Let
$\mathcal{O}_K$
. Let
![]() $p(x) \in K[x]$
be an
$p(x) \in K[x]$
be an
![]() $\mathcal{O}_K$
-valued intersective polynomial. Let
$\mathcal{O}_K$
-valued intersective polynomial. Let
![]() $r,s \in \mathcal{O}_K$
be distinct and nonzero. Then for any ergodic measure-preserving
$r,s \in \mathcal{O}_K$
be distinct and nonzero. Then for any ergodic measure-preserving
![]() $\mathcal{O}_K$
-system
$\mathcal{O}_K$
-system
![]() $\left( X, \mathcal{B}, \mu, T \right)$
,
$\left( X, \mathcal{B}, \mu, T \right)$
,
![]() $A \in \mathcal{B}$
, and
$A \in \mathcal{B}$
, and
![]() $\varepsilon > 0$
, the set
$\varepsilon > 0$
, the set
is
![]() $\text{AVIP}_{0,+}^*$
.
$\text{AVIP}_{0,+}^*$
.
Moreover, if
![]() $\frac{s}{r} \in \mathbb{Q}$
, then
$\frac{s}{r} \in \mathbb{Q}$
, then
is
![]() $\text{AVIP}_{0,+}^*$
.
$\text{AVIP}_{0,+}^*$
.
Acknowledgements
The authors thank Jonathan Lubin for providing a key idea in the proof of Proposition 2·10.