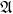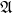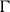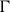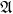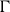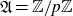Introduction
One of the starting points of tropical geometry is the observation that there is a deep analogy between the classical geometry of Riemann surfaces and the geometry of metric graphs, or more generally, (abstract) tropical curves.
Let X be a Riemann surface and let
![]() $B\subseteq X$
be a finite set. Ramified covers
$B\subseteq X$
be a finite set. Ramified covers
![]() $X'\rightarrow X$
that are branched over B are topological coverings of
$X'\rightarrow X$
that are branched over B are topological coverings of
![]() $X_0=X\setminus B$
, and the Galois correspondence classifies such covers in terms of the fundamental group
$X_0=X\setminus B$
, and the Galois correspondence classifies such covers in terms of the fundamental group
![]() $\pi_1(X_0,x_0)$
for some base point
$\pi_1(X_0,x_0)$
for some base point
![]() $x_0\in X_0$
. This beautiful and classical story is explained in many standard textbooks on Riemann surfaces, such as [
Reference Cavalieri and MilesCM16, Reference MirandaMir95, Reference SzamuelySza09
]. In particular, given a finite group
$x_0\in X_0$
. This beautiful and classical story is explained in many standard textbooks on Riemann surfaces, such as [
Reference Cavalieri and MilesCM16, Reference MirandaMir95, Reference SzamuelySza09
]. In particular, given a finite group
![]() $\mathfrak{G}$
, Galois covers with deck group
$\mathfrak{G}$
, Galois covers with deck group
![]() $\mathfrak{G}$
(not necessarily connected) are in one-to-one correspondence with monodromy representations
$\mathfrak{G}$
(not necessarily connected) are in one-to-one correspondence with monodromy representations
![]() $\pi_1(X_0,x_0)\to \mathfrak{G}$
. If
$\pi_1(X_0,x_0)\to \mathfrak{G}$
. If
![]() $\mathfrak{G}=\mathfrak{A}$
is abelian, the universal coefficient theorem implies that the set of such covers is equal to
$\mathfrak{G}=\mathfrak{A}$
is abelian, the universal coefficient theorem implies that the set of such covers is equal to
Replacing
![]() $H^1$
and
$H^1$
and
![]() $\pi_1$
with their étale counterparts, this correspondence holds over any algebraically closed field k whose characteristic is zero or relatively prime to
$\pi_1$
with their étale counterparts, this correspondence holds over any algebraically closed field k whose characteristic is zero or relatively prime to
![]() $|\mathfrak{A}|$
.
$|\mathfrak{A}|$
.
The natural tropical analogue of a non-constant holomorphic map of Riemann surfaces is a finite harmonic morphism
![]() $\Gamma'\rightarrow\Gamma$
of metric graphs (or tropical curves), which is a continuous map with finite fibers that pulls back harmonic functions on open subsets of
$\Gamma'\rightarrow\Gamma$
of metric graphs (or tropical curves), which is a continuous map with finite fibers that pulls back harmonic functions on open subsets of
![]() $\Gamma$
to harmonic functions on their preimages in
$\Gamma$
to harmonic functions on their preimages in
![]() $\Gamma'$
. Contrary to the algebraic case, a harmonic morphism need not be a topological covering map (even after finitely many points are removed), as harmonic morphisms allow for dilation along edges. Namely, via the natural identification of edges with real intervals, the restriction of a harmonic morphism
$\Gamma'$
. Contrary to the algebraic case, a harmonic morphism need not be a topological covering map (even after finitely many points are removed), as harmonic morphisms allow for dilation along edges. Namely, via the natural identification of edges with real intervals, the restriction of a harmonic morphism
![]() $\phi\;:\;\Gamma'\rightarrow\Gamma$
to an edge
$\phi\;:\;\Gamma'\rightarrow\Gamma$
to an edge
![]() $e'\subset\Gamma'$
is given by
$e'\subset\Gamma'$
is given by
The coefficient
![]() $d\in\mathbb{Z}_{>0}$
is known as the dilation factor of
$d\in\mathbb{Z}_{>0}$
is known as the dilation factor of
![]() $\phi$
along e
′. The behaviour of a harmonic morphism at a vertex
$\phi$
along e
′. The behaviour of a harmonic morphism at a vertex
![]() $v'\in \Gamma'$
is controlled by another phenomenon that we call dilation at vertices, which assigns a dilation factor to each vertex as well (see Section 1 below). We also note that dilation should not be confused with the distinct phenomenon of ramification for morphisms of weighted graphs, which we discuss at the end of Section 1.
$v'\in \Gamma'$
is controlled by another phenomenon that we call dilation at vertices, which assigns a dilation factor to each vertex as well (see Section 1 below). We also note that dilation should not be confused with the distinct phenomenon of ramification for morphisms of weighted graphs, which we discuss at the end of Section 1.
Dilation phenomena are inherent properties of morphisms of metric graphs, and arise naturally in tropicalisation constructions. For this reason, the fundamental group of a metric graph (specifically, its underlying topological space) cannot be used to classify its harmonic covers, and this classification problem is, to the best of our knowledge, currently open.
Classification of abelian tropical covers
Our first goal in this paper is to classify abelian harmonic covers of a fixed metric graph
![]() $\Gamma$
. Given a finite group
$\Gamma$
. Given a finite group
![]() $\mathfrak{G}$
, a harmonic
$\mathfrak{G}$
, a harmonic
![]() $\mathfrak{G}$
-cover of
$\mathfrak{G}$
-cover of
![]() $\Gamma$
is a harmonic morphism
$\Gamma$
is a harmonic morphism
![]() $\phi\;:\;\Gamma'\to \Gamma$
together with a fiberwise
$\phi\;:\;\Gamma'\to \Gamma$
together with a fiberwise
![]() $\mathfrak{G}$
-action, such that the dilation factor of
$\mathfrak{G}$
-action, such that the dilation factor of
![]() $\phi$
at a point
$\phi$
at a point
![]() $p'\in \Gamma'$
is equal to the order of its stabiliser group. If
$p'\in \Gamma'$
is equal to the order of its stabiliser group. If
![]() $\mathfrak{G}=\mathfrak{A}$
is abelian, then
$\mathfrak{G}=\mathfrak{A}$
is abelian, then
![]() $\phi$
admits a convenient cohomological description. Namely, for any
$\phi$
admits a convenient cohomological description. Namely, for any
![]() $p\in \Gamma$
the stabiliser groups of two points of
$p\in \Gamma$
the stabiliser groups of two points of
![]() $\phi^{-1}(p)$
are equal, hence the cover determines a family of subgroups
$\phi^{-1}(p)$
are equal, hence the cover determines a family of subgroups
![]() $D(p)\subseteq \mathfrak{A}$
indexed by
$D(p)\subseteq \mathfrak{A}$
indexed by
![]() $p\in \Gamma$
, an object which we call the
$p\in \Gamma$
, an object which we call the
![]() $\mathfrak{A}$
-dilation datum of the harmonic cover. Choosing a graph model for
$\mathfrak{A}$
-dilation datum of the harmonic cover. Choosing a graph model for
![]() $\Gamma$
, the
$\Gamma$
, the
![]() $\mathfrak{A}$
-dilation datum D determines (by taking quotients) a sheaf of abelian groups
$\mathfrak{A}$
-dilation datum D determines (by taking quotients) a sheaf of abelian groups
![]() $\mathfrak{A}_D$
on
$\mathfrak{A}_D$
on
![]() $\Gamma$
that we call the codilation sheaf.
$\Gamma$
that we call the codilation sheaf.
Theorem A (Theorem 2·3).
Let
![]() $\Gamma$
be a metric graph or tropical curve, let
$\Gamma$
be a metric graph or tropical curve, let
![]() $\mathfrak{A}$
be a finite abelian group, and let D be an
$\mathfrak{A}$
be a finite abelian group, and let D be an
![]() $\mathfrak{A}$
-dilation datum on
$\mathfrak{A}$
-dilation datum on
![]() $\Gamma$
. There is a natural bijection between the sheaf cohomology group
$\Gamma$
. There is a natural bijection between the sheaf cohomology group
![]() $H^1(\Gamma,\mathfrak{A}_D)$
and the set of harmonic
$H^1(\Gamma,\mathfrak{A}_D)$
and the set of harmonic
![]() $\mathfrak{A}$
-covers with
$\mathfrak{A}$
-covers with
![]() $\mathfrak{A}$
-dilation datum D.
$\mathfrak{A}$
-dilation datum D.
We refer to
![]() $H^1(\Gamma,\mathfrak{A}_D)$
as the dilated cohomology group of
$H^1(\Gamma,\mathfrak{A}_D)$
as the dilated cohomology group of
![]() $\Gamma$
with respect to the
$\Gamma$
with respect to the
![]() $\mathfrak{A}$
-dilation datum D. One may consider Theorem A as a first step towards a tropical analogue of geometric class field theory.
$\mathfrak{A}$
-dilation datum D. One may consider Theorem A as a first step towards a tropical analogue of geometric class field theory.
From algebraic to tropical covers (and back again)
There is a natural tropicalisation procedure that associates to a finite cover
![]() $F\colon X'\rightarrow X$
of smooth projective algebraic curves over a non-Archimedean field a harmonic morphism
$F\colon X'\rightarrow X$
of smooth projective algebraic curves over a non-Archimedean field a harmonic morphism
![]() $\phi\colon \Gamma_{X'}\rightarrow\Gamma_X$
between the dual tropical curves. In the literature one may find at least two ways to describe this process: one by restricting the associated map
$\phi\colon \Gamma_{X'}\rightarrow\Gamma_X$
between the dual tropical curves. In the literature one may find at least two ways to describe this process: one by restricting the associated map
![]() $F^{\textrm{an}}\colon X'^{\textrm{an}}\rightarrow X^{\textrm{an}}$
of Berkovich analytic spaces to the non-Archimedean skeletons, as in [
Reference Amini, Baker, Brugallé and RabinoffABBR15a, Reference Amini, Baker, Brugallé and RabinoffABBR15b
], the other from a moduli-theoretic point of view, as in [
Reference Cavalieri, Markwig and RanganathanCMR16
], using the moduli space of admissible covers. In Section 3 below we recall the latter approach, paying extra attention to the role of a finite automorphism group
$F^{\textrm{an}}\colon X'^{\textrm{an}}\rightarrow X^{\textrm{an}}$
of Berkovich analytic spaces to the non-Archimedean skeletons, as in [
Reference Amini, Baker, Brugallé and RabinoffABBR15a, Reference Amini, Baker, Brugallé and RabinoffABBR15b
], the other from a moduli-theoretic point of view, as in [
Reference Cavalieri, Markwig and RanganathanCMR16
], using the moduli space of admissible covers. In Section 3 below we recall the latter approach, paying extra attention to the role of a finite automorphism group
![]() $\mathfrak{G}$
. In particular, we describe how to associate to a
$\mathfrak{G}$
. In particular, we describe how to associate to a
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $F\colon X'\rightarrow X$
of algebraic curves a harmonic
$F\colon X'\rightarrow X$
of algebraic curves a harmonic
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $\phi\colon\Gamma_{X'}\rightarrow\Gamma_X$
of tropical curves.
$\phi\colon\Gamma_{X'}\rightarrow\Gamma_X$
of tropical curves.
Describing finite harmonic covers that arise as tropicalisations of finite algebraic covers is a highly non-trivial task, known as the realisability problem. We refer the reader to [
Reference CaporasoCap14
] and [
Reference Cavalieri, Markwig and RanganathanCMR16
] for details, including the connection to the still-open Hurwitz existence problem from the classical topology of Riemann surfaces (see [
Reference Pervova and PetronioPP06
] for a survey). In the abelian case, however, this problem admits a convenient homological solution, which we describe in Section 4. Given a tropical curve
![]() $\Gamma$
and a finite abelian group
$\Gamma$
and a finite abelian group
![]() $\mathfrak{A}$
, we introduce the extended homology group
$\mathfrak{A}$
, we introduce the extended homology group
![]() $H_1^{\textrm{ext}}(\Gamma,\mathfrak{A})$
whose elements encode local monodromy data of harmonic
$H_1^{\textrm{ext}}(\Gamma,\mathfrak{A})$
whose elements encode local monodromy data of harmonic
![]() $\mathfrak{A}$
-covers of
$\mathfrak{A}$
-covers of
![]() $\Gamma$
. In particular, a class
$\Gamma$
. In particular, a class
![]() $\eta \in H_1^{\textrm{ext}}(\Gamma,\mathfrak{A})$
determines an associated
$\eta \in H_1^{\textrm{ext}}(\Gamma,\mathfrak{A})$
determines an associated
![]() $\mathfrak{A}$
-dilation datum
$\mathfrak{A}$
-dilation datum
![]() $D_\eta$
, and the realisable covers are exactly the ones that have such
$D_\eta$
, and the realisable covers are exactly the ones that have such
![]() $\mathfrak{A}$
-dilation data:
$\mathfrak{A}$
-dilation data:
Theorem B (Theorem 4·4).
A harmonic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $\Gamma'\to \Gamma$
of tropical curves is realisable over a non-Archimedean field of residue characteristic zero or coprime to
$\Gamma'\to \Gamma$
of tropical curves is realisable over a non-Archimedean field of residue characteristic zero or coprime to
![]() $\vert \mathfrak{A}\vert$
if and only if its
$\vert \mathfrak{A}\vert$
if and only if its
![]() $\mathfrak{A}$
-dilation datum is associated to a class in the extended homology group
$\mathfrak{A}$
-dilation datum is associated to a class in the extended homology group
![]() $H_1^{\textrm{ext}}(\Gamma,\mathfrak{A})$
.
$H_1^{\textrm{ext}}(\Gamma,\mathfrak{A})$
.
In Section 5, we specialise to the case of cyclic covers of prime order. It turns out that our realisability criterion is closely related to the so-called nowhere-zero flow problem from graph theory. In particular, Tutte’s 5-flow conjecture has an equivalent formulation in terms of the existence of everywhere-dilated
![]() $\mathbb{Z}/5\mathbb{Z}$
-covers.
$\mathbb{Z}/5\mathbb{Z}$
-covers.
We briefly mention how our results may generalise to the case of a non-abelian group
![]() $\mathfrak{G}$
. A harmonic
$\mathfrak{G}$
. A harmonic
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $\Gamma'\to \Gamma$
determines the structure of a graph of groups on a model of
$\Gamma'\to \Gamma$
determines the structure of a graph of groups on a model of
![]() $\Gamma$
, and Bass–Serre theory classifies such covers in terms of an appropriately generalised fundamental group [
Reference SerreSer80, Reference BassBas93
]. However, there is no convenient generalisation of the homological realisability criterion, and the difficulties stemming from the Hurwitz existence problem cannot be avoided.
$\Gamma$
, and Bass–Serre theory classifies such covers in terms of an appropriately generalised fundamental group [
Reference SerreSer80, Reference BassBas93
]. However, there is no convenient generalisation of the homological realisability criterion, and the difficulties stemming from the Hurwitz existence problem cannot be avoided.
Earlier and related works
Graphs and tropical curves with group actions have been studied by a number of authors. The simplest example is the case of tropical hyperelliptic curves, which are
![]() $\mathbb{Z}/2\mathbb{Z}$
-covers of a tree (see [
Reference Amini, Baker, Brugallé and RabinoffABBR15b, Reference Bolognese, Brandt and ChuaBBC17, Reference Baker and NorineBN09, Reference CaporasoCap14, Reference ChanCha13, Reference LenLen17, Reference PanizzutPan16
]). Expanding on this, Brandt and Helminck [
Reference Brandt and Alexander HelminckBH20
] consider arbitrary cyclic covers of a tree. Helminck [
Reference Alexander HelminckHel17
] looks at the tropicalisation of arbitrary abelian covers of algebraic curves from a non-Archimedean perspective, as in [
Reference Amini, Baker, Brugallé and RabinoffABBR15a, Reference Amini, Baker, Brugallé and RabinoffABBR15b
]. Our Section 3 provides a moduli-theoretic approach to the same topic (with possibly non-abelian group) in the spirit of [
Reference Cavalieri, Markwig and RanganathanCMR16
].
$\mathbb{Z}/2\mathbb{Z}$
-covers of a tree (see [
Reference Amini, Baker, Brugallé and RabinoffABBR15b, Reference Bolognese, Brandt and ChuaBBC17, Reference Baker and NorineBN09, Reference CaporasoCap14, Reference ChanCha13, Reference LenLen17, Reference PanizzutPan16
]). Expanding on this, Brandt and Helminck [
Reference Brandt and Alexander HelminckBH20
] consider arbitrary cyclic covers of a tree. Helminck [
Reference Alexander HelminckHel17
] looks at the tropicalisation of arbitrary abelian covers of algebraic curves from a non-Archimedean perspective, as in [
Reference Amini, Baker, Brugallé and RabinoffABBR15a, Reference Amini, Baker, Brugallé and RabinoffABBR15b
]. Our Section 3 provides a moduli-theoretic approach to the same topic (with possibly non-abelian group) in the spirit of [
Reference Cavalieri, Markwig and RanganathanCMR16
].
In a different direction, Jensen and Len [
Reference Jensen and LenJL18
] consider
![]() $\mathbb{Z}/2\mathbb{Z}$
-covers of arbitrary tropical curves, and define the tropical Prym variety associated to such a cover. This object is equipped with a canonical polyhedral decomposition, leading to a combinatorial formula for its volume [
Reference Ghosh and ZakharovGZ23, Reference Len and ZakharovLZ22
]. A tropical version of Donagi’s n-gonal construction is investigated in [
Reference Röhrle and ZakharovRZ22
]. Applications to algebraic Prym–Brill–Noether theory are studied in [
Reference Len and UlirschLU21
] and [
Reference Creech, Len, Ritter and WuCLRW22
]. See [
Reference LenLen22
] for a survey on tropical Prym varieties. In a similar vein, Song [
Reference SongSon19
] considers
$\mathbb{Z}/2\mathbb{Z}$
-covers of arbitrary tropical curves, and define the tropical Prym variety associated to such a cover. This object is equipped with a canonical polyhedral decomposition, leading to a combinatorial formula for its volume [
Reference Ghosh and ZakharovGZ23, Reference Len and ZakharovLZ22
]. A tropical version of Donagi’s n-gonal construction is investigated in [
Reference Röhrle and ZakharovRZ22
]. Applications to algebraic Prym–Brill–Noether theory are studied in [
Reference Len and UlirschLU21
] and [
Reference Creech, Len, Ritter and WuCLRW22
]. See [
Reference LenLen22
] for a survey on tropical Prym varieties. In a similar vein, Song [
Reference SongSon19
] considers
![]() $\mathfrak{G}$
-invariant linear systems with the goal of studying their descent properties to the quotient.
$\mathfrak{G}$
-invariant linear systems with the goal of studying their descent properties to the quotient.
In [
Reference Alexander HelminckHel21
] Helminck studies the fundamental group of a metrised curve complex in the sense of Amini and Baker [
Reference Amini and BakerAB15
] (which are also crucially used in [
Reference Amini, Baker, Brugallé and RabinoffABBR15a, Reference Amini, Baker, Brugallé and RabinoffABBR15b
]). In his framework he proves a result that amounts to identifying the fundamental group of a metrised curve complex with the étale fundamental group of the generic fiber of its smoothing. Theorem B could have been proved using this framework, but we decided to use the moduli-theoretic approach of [
Reference Cavalieri, Markwig and RanganathanCMR16
] via
![]() $\mathfrak{G}$
-admissible covers in the sense of [
Reference Abramovich, Corti and VistoliACV03
].
$\mathfrak{G}$
-admissible covers in the sense of [
Reference Abramovich, Corti and VistoliACV03
].
Helminck’s result provides a new perspective on an older result of Sadi [ Reference SaïdiSaï97 ], which identifies the étale fundamental group of the generic fiber with the profinite completion of the fundamental group of a suitable graph of groups (in the sense of Bass and Serre [ Reference BassBas93, Reference SerreSer80 ]) that encodes the fundamental group of a metrised curve complex. From a moduli-theoretic perspective, a similar observation seems to be inherent in both [ Reference Bertin and RomagnyBR11 ] and [ Reference EkedahlEke95 ].
From a moduli-theoretic perspective, studying degenerations of
![]() $\mathfrak{G}$
-covers of algebraic curves is equivalent to studying the compactification of the moduli space of
$\mathfrak{G}$
-covers of algebraic curves is equivalent to studying the compactification of the moduli space of
![]() $\mathfrak{G}$
-covers in terms of the moduli space of
$\mathfrak{G}$
-covers in terms of the moduli space of
![]() $\mathfrak{G}$
-admissible covers, as constructed in [
Reference Abramovich, Corti and VistoliACV03
] and [
Reference Bertin and RomagnyBR11
]. In [
Reference Bertin and RomagnyBR11
, section 7] the authors have already introduced a graph-theoretic gadget to understand the boundary strata of this moduli space: so-called modular graphs with an action of a finite (not necessarily abelian) group
$\mathfrak{G}$
-admissible covers, as constructed in [
Reference Abramovich, Corti and VistoliACV03
] and [
Reference Bertin and RomagnyBR11
]. In [
Reference Bertin and RomagnyBR11
, section 7] the authors have already introduced a graph-theoretic gadget to understand the boundary strata of this moduli space: so-called modular graphs with an action of a finite (not necessarily abelian) group
![]() $\mathfrak{G}$
.
$\mathfrak{G}$
.
This idea seems to have appeared independently in other works as well: Chiodo and Farkas [
Reference Chiodo and FarkasCF17
] study the boundary of the moduli space of level curves, which is equivalent to a component of the moduli space of
![]() $\mathfrak{G}$
-admissible covers for a cyclic group
$\mathfrak{G}$
-admissible covers for a cyclic group
![]() $\mathfrak{G}$
, and look at cyclic covers of an arbitrary graph. Their work has been extended to an arbitrary finite group
$\mathfrak{G}$
, and look at cyclic covers of an arbitrary graph. Their work has been extended to an arbitrary finite group
![]() $\mathfrak{G}$
by Galeotti in [
Reference GaleottiGal19a, Reference GaleottiGal19b
]. Finally, in [
Reference Schmitt and van ZelmSvZ20
], Schmitt and van Zelm apply a graph-theoretic approach to the boundary of the moduli space of
$\mathfrak{G}$
by Galeotti in [
Reference GaleottiGal19a, Reference GaleottiGal19b
]. Finally, in [
Reference Schmitt and van ZelmSvZ20
], Schmitt and van Zelm apply a graph-theoretic approach to the boundary of the moduli space of
![]() $\mathfrak{G}$
-admissible covers (for an arbitrary finite group
$\mathfrak{G}$
-admissible covers (for an arbitrary finite group
![]() $\mathfrak{G}$
) to study their pushforward classes in the tautological ring of
$\mathfrak{G}$
) to study their pushforward classes in the tautological ring of
![]() $\overline{\mathcal{M}}_{g,n}$
.
$\overline{\mathcal{M}}_{g,n}$
.
In [
Reference Cavalieri, Markwig and RanganathanCMR16
] Cavalieri, Markwig and Ranganathan develop a moduli-theoretic approach to the tropicalisation of the moduli space of admissible covers (without a fixed group operation). In [
Reference Caporaso, Melo and PaciniCMP20
], Caporaso, Melo and Pacini study the tropicalisation of the moduli space of spin curves, which, in view of the results in [
Reference Jensen and LenJL18
], is closely related to our story in the case
![]() $\mathfrak{G}=\mathbb{Z}/2\mathbb{Z}$
.
$\mathfrak{G}=\mathbb{Z}/2\mathbb{Z}$
.
The problem of classifying covers of a graph with an action of a given group (not necessarily abelian) was studied by Corry in [ Reference CorryCor11, Reference CorryCor12, Reference CorryCor15 ]. However, Corry considered a different category of graph morphisms, allowing edge contraction but not dilation. To the best of our knowledge, no author has considered the problem of classifying all covers of a given graph with an action of a fixed group.
1. Harmonic covers of metric graphs and tropical curves
In this section, we recall a number of standard definitions concerning graphs, tropical curves, harmonic morphisms and group actions on graphs.
1·1. Finite graphs and harmonic morphisms
We use a modified version of Serre’s definition of a graph [ Reference SerreSer80 ] that allows for legs, which are a type of extremal edge with no end vertex.
Definition 1·1. A graph with legs G, or simply a graph, consists of the following data:
-
(i) a finite set X(G);
-
(ii) an idempotent root map
 $r\;:\;X(G)\to X(G)$
;
$r\;:\;X(G)\to X(G)$
; -
(iii) an involution
 $\iota\;:\;X(G)\to X(G)$
whose fixed set contains the image of r.
$\iota\;:\;X(G)\to X(G)$
whose fixed set contains the image of r.
The set X(G) is the union of the vertices V(G) and half-edges H(G) of the graph G, where V(G) is the image of r and
![]() $H(G)=X(G)\backslash V(G)$
is the complement. The involution
$H(G)=X(G)\backslash V(G)$
is the complement. The involution
![]() $\iota$
preserves H(G) and partitions it into orbits of sizes 1 and 2; we call these respectively the legs and edges of G and denote the corresponding sets by L(G) and E(G). The root map assigns one root vertex to each leg and two root vertices to each edge (each vertex is rooted at itself). A loop is an edge whose root vertices coincide. An orientation on G is a choice of order (h,h
′) on each edge
$\iota$
preserves H(G) and partitions it into orbits of sizes 1 and 2; we call these respectively the legs and edges of G and denote the corresponding sets by L(G) and E(G). The root map assigns one root vertex to each leg and two root vertices to each edge (each vertex is rooted at itself). A loop is an edge whose root vertices coincide. An orientation on G is a choice of order (h,h
′) on each edge
![]() $e=\{h,h'\}$
of G and defines source and target maps
$e=\{h,h'\}$
of G and defines source and target maps
![]() $s,t\;:\;E(G)\to V(G)$
by
$s,t\;:\;E(G)\to V(G)$
by
![]() $s(e)=r(h)$
and
$s(e)=r(h)$
and
![]() $t(e)=r(h')$
. We note that a leg does not have a vertex at its free end and is thus distinct from an extremal edge, and that legs do not require orienting.
$t(e)=r(h')$
. We note that a leg does not have a vertex at its free end and is thus distinct from an extremal edge, and that legs do not require orienting.
Graphs with legs naturally appear in tropical moduli problems, where a leg represents the tropicalisation of a marked point. An extremal edge, on the other hand, represents an irreducible component attached to the rest of the curve at a single node.
The tangent space
![]() $T_v G$
and valency
$T_v G$
and valency
![]() $\textrm{val} (v)$
of a vertex
$\textrm{val} (v)$
of a vertex
![]() $v\in V(G)$
are defined by
$v\in V(G)$
are defined by
so that a leg is counted once for valency, while a loop is counted twice.
A morphism of graphs
![]() $f\;:\;G'\to G$
, is a set map
$f\;:\;G'\to G$
, is a set map
![]() $f\;:\;X(G')\to X(G)$
that commutes with the root and involution maps and that sends vertices to vertices, edges to edges, and legs to legs. By abuse of notation, we denote by f the corresponding maps on the vertices, half-edges, edges, and legs. We note that our graph morphisms are finite and do not allow edges or legs to contract to vertices. Non-finite morphisms are relevant to tropical geometry, but do not occur as quotients by finite group actions; so we do not consider them.
$f\;:\;X(G')\to X(G)$
that commutes with the root and involution maps and that sends vertices to vertices, edges to edges, and legs to legs. By abuse of notation, we denote by f the corresponding maps on the vertices, half-edges, edges, and legs. We note that our graph morphisms are finite and do not allow edges or legs to contract to vertices. Non-finite morphisms are relevant to tropical geometry, but do not occur as quotients by finite group actions; so we do not consider them.
Let G and G
′ be graphs. A harmonic morphism
![]() $(f,d_f)$
consists of a graph morphism
$(f,d_f)$
consists of a graph morphism
![]() $f\;:\;G'\to G$
and a degree assignment
$f\;:\;G'\to G$
and a degree assignment
![]() $d_f\;:\;X(G')\to \mathbb{Z}_{>0}$
such that
$d_f\;:\;X(G')\to \mathbb{Z}_{>0}$
such that
![]() $d_f(h'_{1})=d_f(h'_{2})$
for each edge
$d_f(h'_{1})=d_f(h'_{2})$
for each edge
![]() $e'=\{h'_{1},h'_{2}\}\in E(G')$
(a quantity that we denote by
$e'=\{h'_{1},h'_{2}\}\in E(G')$
(a quantity that we denote by
![]() $d_f(e')$
), and such that
$d_f(e')$
), and such that
for every
![]() $v'\in V(G')$
and every
$v'\in V(G')$
and every
![]() $h\in T_{f(v)}G$
. In particular, the quantity appearing on the right-hand side of (2) does not depend on the choice of
$h\in T_{f(v)}G$
. In particular, the quantity appearing on the right-hand side of (2) does not depend on the choice of
![]() $h\in T_{f(v)}G$
. The degree
$h\in T_{f(v)}G$
. The degree
![]() $d_f$
is also called the dilation factor of f. If G is connected, then the global degree of f is defined as
$d_f$
is also called the dilation factor of f. If G is connected, then the global degree of f is defined as
for any choice of
![]() $v\in V(G)$
,
$v\in V(G)$
,
![]() $e\in E(G)$
or
$e\in E(G)$
or
![]() $l\in L(G)$
. A harmonic morphism
$l\in L(G)$
. A harmonic morphism
![]() $(f,d_f)$
is called free if
$(f,d_f)$
is called free if
![]() $d_f(x)=1$
for all
$d_f(x)=1$
for all
![]() $x\in X(G)$
; a free harmonic morphism is a covering space in the topological sense.
$x\in X(G)$
; a free harmonic morphism is a covering space in the topological sense.
1·2. Group quotients and harmonic Galois covers
An automorphism of a graph G is a morphism
![]() $f\;:\;G\to G$
that has an inverse; such a morphism can be made harmonic by setting
$f\;:\;G\to G$
that has an inverse; such a morphism can be made harmonic by setting
![]() $d_f=1$
everywhere. A priori, a non-trivial automorphism may flip edges, in other words exchange the two half-edges making up an edge. Such automorphisms do not give rise to a quotient, however, since we do not allow an edge to map to a leg. Hence we exclude them from consideration.
$d_f=1$
everywhere. A priori, a non-trivial automorphism may flip edges, in other words exchange the two half-edges making up an edge. Such automorphisms do not give rise to a quotient, however, since we do not allow an edge to map to a leg. Hence we exclude them from consideration.
Definition 1·2. Let G be a graph and
![]() $\mathfrak{G}$
a finite group. A
$\mathfrak{G}$
a finite group. A
![]() $\mathfrak{G}$
-action on G is a homomorphism from
$\mathfrak{G}$
-action on G is a homomorphism from
![]() $\mathfrak{G}$
to the automorphism group
$\mathfrak{G}$
to the automorphism group
![]() $\textrm{Aut} (G)$
, such that, for every
$\textrm{Aut} (G)$
, such that, for every
![]() $g\in \mathfrak{G}$
and every
$g\in \mathfrak{G}$
and every
![]() $e=\{h,h'\}\in E(G)$
, we have
$e=\{h,h'\}\in E(G)$
, we have
![]() $g(h)\neq h'$
(so that either
$g(h)\neq h'$
(so that either
![]() $g(h)=h$
and
$g(h)=h$
and
![]() $g(h')=h'$
, or
$g(h')=h'$
, or
![]() $g(e)\neq e$
).
$g(e)\neq e$
).
Given a
![]() $\mathfrak{G}$
-action on a graph G, we can naturally form the quotient graph
$\mathfrak{G}$
-action on a graph G, we can naturally form the quotient graph
![]() $G/\mathfrak{G}$
in such a way that the quotient map
$G/\mathfrak{G}$
in such a way that the quotient map
![]() $f\;:\;G\to G/\mathfrak{G}$
is harmonic of degree
$f\;:\;G\to G/\mathfrak{G}$
is harmonic of degree
![]() $|\mathfrak{G}|$
.
$|\mathfrak{G}|$
.
Definition 1·3. Let G be a graph and let
![]() $\mathfrak{G}$
be a finite group. Given a
$\mathfrak{G}$
be a finite group. Given a
![]() $\mathfrak{G}$
-action on G, we define the quotient graph
$\mathfrak{G}$
-action on G, we define the quotient graph
![]() $G/\mathfrak{G}$
by setting
$G/\mathfrak{G}$
by setting
![]() $X(G/\mathfrak{G})=X(G)/\mathfrak{G}$
. The root and involution maps on G are
$X(G/\mathfrak{G})=X(G)/\mathfrak{G}$
. The root and involution maps on G are
![]() $\mathfrak{G}$
-invariant and descend to
$\mathfrak{G}$
-invariant and descend to
![]() $X(G/\mathfrak{G})$
. It is clear that
$X(G/\mathfrak{G})$
. It is clear that
![]() $V(G/\mathfrak{G})=V(G)/\mathfrak{G}$
and
$V(G/\mathfrak{G})=V(G)/\mathfrak{G}$
and
![]() $H(G/\mathfrak{G})=H(G)/\mathfrak{G}$
, and by assumption the
$H(G/\mathfrak{G})=H(G)/\mathfrak{G}$
, and by assumption the
![]() $\mathfrak{G}$
-action does not identify the two half-edges of any edge of G. Therefore
$\mathfrak{G}$
-action does not identify the two half-edges of any edge of G. Therefore
![]() $E(G/\mathfrak{G})=E(G)/\mathfrak{G}$
and
$E(G/\mathfrak{G})=E(G)/\mathfrak{G}$
and
![]() $L(G/\mathfrak{G})=L(G)/\mathfrak{G}$
, and the quotient map
$L(G/\mathfrak{G})=L(G)/\mathfrak{G}$
, and the quotient map
is a finite morphism. By the orbit-stabiliser theorem, we can promote f to a harmonic morphism of global degree
![]() $\deg(f)=|\mathfrak{G}|$
by setting
$\deg(f)=|\mathfrak{G}|$
by setting
![]() $d_f(x)=|\mathfrak{G}_x|$
, where
$d_f(x)=|\mathfrak{G}_x|$
, where
![]() $\mathfrak{G}_x$
is the stabiliser subgroup of
$\mathfrak{G}_x$
is the stabiliser subgroup of
![]() $x\in X(G)$
.
$x\in X(G)$
.
We now define a harmonic Galois cover of a graph to be any harmonic morphism obtained in this way.
Definition 1·4. Let G be a graph and let
![]() $\mathfrak{G}$
be a finite group of order d. A harmonic
$\mathfrak{G}$
be a finite group of order d. A harmonic
![]() $\mathfrak{G}$
-cover of G is a harmonic morphism
$\mathfrak{G}$
-cover of G is a harmonic morphism
![]() $f\colon G'\rightarrow G$
of degree d together with a
$f\colon G'\rightarrow G$
of degree d together with a
![]() $\mathfrak{G}$
-action on G
′ such that following axioms hold:
$\mathfrak{G}$
-action on G
′ such that following axioms hold:
-
(i) the harmonic morphism f is
 $\mathfrak{G}$
-invariant, in other words
$\mathfrak{G}$
-invariant, in other words
 $f(g(x'))=f(x')$
and
$f(g(x'))=f(x')$
and
 $d_f(g(x'))=d_f(x')$
for all
$d_f(g(x'))=d_f(x')$
for all
 $x'\in X(G')$
and all
$x'\in X(G')$
and all
 $g\in \mathfrak{G}$
;
$g\in \mathfrak{G}$
; -
(ii) for all
 $x\in X(G)$
, the group
$x\in X(G)$
, the group
 $\mathfrak{G}$
acts transitively on the fiber
$\mathfrak{G}$
acts transitively on the fiber
 $f^{-1}(x)$
.
$f^{-1}(x)$
.
Let
![]() $f\;:\;G'\to G$
be a harmonic
$f\;:\;G'\to G$
be a harmonic
![]() $\mathfrak{G}$
-cover, and pick a vertex or half-edge
$\mathfrak{G}$
-cover, and pick a vertex or half-edge
![]() $x\in X(G)$
. The group
$x\in X(G)$
. The group
![]() $\mathfrak{G}$
acts transitively on the fiber
$\mathfrak{G}$
acts transitively on the fiber
![]() $f^{-1}(x)$
, so we can identify the latter with
$f^{-1}(x)$
, so we can identify the latter with
![]() $\mathfrak{G}/\mathfrak{G}_{x'}$
, where
$\mathfrak{G}/\mathfrak{G}_{x'}$
, where
![]() $\mathfrak{G}_{x'}$
is the stabiliser of some
$\mathfrak{G}_{x'}$
is the stabiliser of some
![]() $x'\in f^{-1}(x)$
. On the other hand, for any
$x'\in f^{-1}(x)$
. On the other hand, for any
![]() $x',x''\in f^{-1}(x)$
we have
$x',x''\in f^{-1}(x)$
we have
![]() $|\mathfrak{G}_{x'}|=|\mathfrak{G}_{x''}|$
and
$|\mathfrak{G}_{x'}|=|\mathfrak{G}_{x''}|$
and
![]() $d_f(x')=d_f(x'')$
. Since the degrees of f on the fiber
$d_f(x')=d_f(x'')$
. Since the degrees of f on the fiber
![]() $f^{-1}(x)$
add up to
$f^{-1}(x)$
add up to
![]() $\deg f=|\mathfrak{G}|$
, it follows that
$\deg f=|\mathfrak{G}|$
, it follows that
![]() $d_f(x')=|\mathfrak{G}_{x'}|$
for any
$d_f(x')=|\mathfrak{G}_{x'}|$
for any
![]() $x'\in X(G')$
. It follows that f is the quotient morphism
$x'\in X(G')$
. It follows that f is the quotient morphism
![]() $G'\to G'/\mathfrak{G}$
.
$G'\to G'/\mathfrak{G}$
.
1·3. Metric graphs
Let G be a graph and let
![]() $\ell\;:\;E(G)\to \mathbb{R}_{>0}$
be an assignment of positive real lengths to the edges of G. The pair
$\ell\;:\;E(G)\to \mathbb{R}_{>0}$
be an assignment of positive real lengths to the edges of G. The pair
![]() $(G,\ell)$
, known as a model for G, determines a metric graph
$(G,\ell)$
, known as a model for G, determines a metric graph
![]() $\Gamma$
by gluing a closed line segment
$\Gamma$
by gluing a closed line segment
![]() $[0,\ell(e)]$
for each edge
$[0,\ell(e)]$
for each edge
![]() $e\in E(G)$
and an open infinite interval
$e\in E(G)$
and an open infinite interval
![]() $[0,\infty)$
for each leg
$[0,\infty)$
for each leg
![]() $l\in L(G)$
in accordance with the structure of G. We equip
$l\in L(G)$
in accordance with the structure of G. We equip
![]() $\Gamma$
with the shortest-path metric. We note that the set of legs does not depend on the choice of model and that the metric graph
$\Gamma$
with the shortest-path metric. We note that the set of legs does not depend on the choice of model and that the metric graph
![]() $\Gamma$
is compact if and only if G has no legs.
$\Gamma$
is compact if and only if G has no legs.
A model
![]() $(G,\ell)$
of a metric graph
$(G,\ell)$
of a metric graph
![]() $\Gamma$
is called simple if G has no loops or multi-edges. Given a simple model
$\Gamma$
is called simple if G has no loops or multi-edges. Given a simple model
![]() $(G,\ell)$
for
$(G,\ell)$
for
![]() $\Gamma$
, we define the star cover
$\Gamma$
, we define the star cover
of
![]() $\Gamma$
as follows. For each leg
$\Gamma$
as follows. For each leg
![]() $l\in L(G)$
, let
$l\in L(G)$
, let
![]() $U_l\subset \Gamma$
be the interior of the corresponding infinite segment in
$U_l\subset \Gamma$
be the interior of the corresponding infinite segment in
![]() $\Gamma$
. For each vertex
$\Gamma$
. For each vertex
![]() $v\in V(G)$
, let
$v\in V(G)$
, let
![]() $U_v\subset \Gamma$
be the union of v and the interiors of all legs and edges incident to v. The distinct
$U_v\subset \Gamma$
be the union of v and the interiors of all legs and edges incident to v. The distinct
![]() $U_l$
have empty intersections, and
$U_l$
have empty intersections, and
![]() $U_l\cap U_v=U_l$
if l is rooted at v and is empty otherwise. Finally, for distinct vertices v and w, the intersection
$U_l\cap U_v=U_l$
if l is rooted at v and is empty otherwise. Finally, for distinct vertices v and w, the intersection
![]() $U_v\cap U_w$
is either the open edge connecting v and w, if there is such an edge, or is empty otherwise. Hence each element of
$U_v\cap U_w$
is either the open edge connecting v and w, if there is such an edge, or is empty otherwise. Hence each element of
![]() $\mathcal{U}(G)$
is contractible, pairwise intersections are open intervals or empty, and all triple intersections are empty, making the star cover convenient for cohomological calculations.
$\mathcal{U}(G)$
is contractible, pairwise intersections are open intervals or empty, and all triple intersections are empty, making the star cover convenient for cohomological calculations.
We now define harmonic morphisms and Galois covers of metric graphs. Let
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma'$
be metric graphs with models G and G
′, respectively. Let
$\Gamma'$
be metric graphs with models G and G
′, respectively. Let
![]() $f\;:\;G'\to G$
be a harmonic morphism of graphs satisfying the condition
$f\;:\;G'\to G$
be a harmonic morphism of graphs satisfying the condition
for all
![]() $e'\in E(G')$
. We define an associated continuous map
$e'\in E(G')$
. We define an associated continuous map
![]() $\phi\;:\;\Gamma'\to \Gamma$
of metric graphs by mapping vertices to vertices, edges to edges, and legs to legs according to f. Along each edge and leg of
$\phi\;:\;\Gamma'\to \Gamma$
of metric graphs by mapping vertices to vertices, edges to edges, and legs to legs according to f. Along each edge and leg of
![]() $\Gamma'$
, the map
$\Gamma'$
, the map
![]() $\phi$
is linear with positive integer slope, or dilation factor, given by the degree
$\phi$
is linear with positive integer slope, or dilation factor, given by the degree
![]() $d_f$
(which we also denote
$d_f$
(which we also denote
![]() $d_{\phi}$
). Condition (3) ensures that
$d_{\phi}$
). Condition (3) ensures that
![]() $\phi$
is continuous, and no condition is required along the infinite legs.
$\phi$
is continuous, and no condition is required along the infinite legs.
A harmonic morphism of metric graphs
![]() $\phi\;:\;\Gamma'\to \Gamma$
is any continuous, piecewise-linear map obtained in this manner, with nonzero integer slopes given by the degree function
$\phi\;:\;\Gamma'\to \Gamma$
is any continuous, piecewise-linear map obtained in this manner, with nonzero integer slopes given by the degree function
![]() $d_f$
of a harmonic morphism of graphs
$d_f$
of a harmonic morphism of graphs
![]() $f\;:\;G'\to G$
(and thus satisfying the balancing condition (2) at each vertex of
$f\;:\;G'\to G$
(and thus satisfying the balancing condition (2) at each vertex of
![]() $\Gamma'$
). This definition is equivalent to requiring that
$\Gamma'$
). This definition is equivalent to requiring that
![]() $\phi$
pulls back harmonic functions on
$\phi$
pulls back harmonic functions on
![]() $\Gamma$
to harmonic functions on
$\Gamma$
to harmonic functions on
![]() $\Gamma'$
. We refer to the datum
$\Gamma'$
. We refer to the datum
![]() $(G,G',f\;:\;G'\to G,d_f)$
as a model for
$(G,G',f\;:\;G'\to G,d_f)$
as a model for
![]() $\phi$
. We say that
$\phi$
. We say that
![]() $\phi$
is free if f is free, or equivalently, if
$\phi$
is free if f is free, or equivalently, if
![]() $\phi$
is a covering isometry.
$\phi$
is a covering isometry.
We similarly define harmonic Galois covers of metric graphs.
Definition 1·5. Let
![]() $\Gamma$
be a metric graph and let
$\Gamma$
be a metric graph and let
![]() $\mathfrak{G}$
be a finite group of order d. A harmonic
$\mathfrak{G}$
be a finite group of order d. A harmonic
![]() $\mathfrak{G}$
-cover of
$\mathfrak{G}$
-cover of
![]() $\Gamma$
is a harmonic morphism
$\Gamma$
is a harmonic morphism
![]() $\phi\colon \Gamma'\rightarrow \Gamma$
of degree d together with an operation of
$\phi\colon \Gamma'\rightarrow \Gamma$
of degree d together with an operation of
![]() $\mathfrak{G}$
on
$\mathfrak{G}$
on
![]() $\Gamma'$
by invertible isometries such that following properties hold:
$\Gamma'$
by invertible isometries such that following properties hold:
-
(i) the harmonic cover
 $\phi$
is
$\phi$
is
 $\mathfrak{G}$
-invariant, i.e.
$\mathfrak{G}$
-invariant, i.e.
 $\phi(g(p'))=\phi(p')$
for all
$\phi(g(p'))=\phi(p')$
for all
 $p'\in \Gamma'$
and all
$p'\in \Gamma'$
and all
 $g\in \mathfrak{G}$
;
$g\in \mathfrak{G}$
; -
(ii) for all
 $p\in\Gamma$
, the group
$p\in\Gamma$
, the group
 $\mathfrak{G}$
operates transitively on the fiber
$\mathfrak{G}$
operates transitively on the fiber
 $\phi^{-1}(p)$
.
$\phi^{-1}(p)$
.
It is clear that a harmonic
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $\phi\;:\;\Gamma'\to\Gamma$
of metric graphs admits a model
$\phi\;:\;\Gamma'\to\Gamma$
of metric graphs admits a model
![]() $f\;:\;G'\to G$
that is a harmonic
$f\;:\;G'\to G$
that is a harmonic
![]() $\mathfrak{G}$
-cover of finite graphs (the models G
′ and G need to be sufficiently fine to avoid edge-flipping). For any
$\mathfrak{G}$
-cover of finite graphs (the models G
′ and G need to be sufficiently fine to avoid edge-flipping). For any
![]() $p'\in \Gamma'$
, the degree
$p'\in \Gamma'$
, the degree
![]() $d_\phi(p')$
is equal to the order of the stabiliser group
$d_\phi(p')$
is equal to the order of the stabiliser group
![]() $\mathfrak{G}_{p'}$
.
$\mathfrak{G}_{p'}$
.
1·4. Weighted graphs, tropical curves and ramification
Graphs and metric graphs that arise as tropicalisations of algebraic curves come equipped with an additional vertex weight function that records local genera. These weights allow us to capture the auxiliary phenomenon of ramification for harmonic morphisms. We recall the definitions.
A weighted graph is a pair (G,g), where G is a finite graph and
![]() $g\;:\;V(G)\to \mathbb{Z}_{\geq 0}$
is a function, where g(v) is called the genus of the vertex v. Similarly, a tropical curve
$g\;:\;V(G)\to \mathbb{Z}_{\geq 0}$
is a function, where g(v) is called the genus of the vertex v. Similarly, a tropical curve
![]() $(\Gamma,g)$
is a metric graph
$(\Gamma,g)$
is a metric graph
![]() $\Gamma$
together with a function
$\Gamma$
together with a function
![]() $g\;:\;\Gamma\to \mathbb{Z}_{\geq 0}$
with finite support. When choosing a model
$g\;:\;\Gamma\to \mathbb{Z}_{\geq 0}$
with finite support. When choosing a model
![]() $(G,\ell)$
for a tropical curve
$(G,\ell)$
for a tropical curve
![]() $(\Gamma,g)$
, we assume that each point
$(\Gamma,g)$
, we assume that each point
![]() $x\in \Gamma$
with
$x\in \Gamma$
with
![]() $g(x)>0$
corresponds to a vertex, and not to an interior point of an edge or a leg, so that (G, g) is a weighted graph. A harmonic morphism of tropical curves is a harmonic map of the underlying metric graphs.
$g(x)>0$
corresponds to a vertex, and not to an interior point of an edge or a leg, so that (G, g) is a weighted graph. A harmonic morphism of tropical curves is a harmonic map of the underlying metric graphs.
Let (G, g) be a weighted graph. We define the Euler characteristic
![]() $\chi(v)$
of a vertex
$\chi(v)$
of a vertex
![]() $v\in V(G)$
as
$v\in V(G)$
as
Now let
![]() $f\;:\;G'\to G$
be a harmonic morphism of weighted graphs (G
′, g
′) and (G, g). We define the ramification degree of f at a vertex
$f\;:\;G'\to G$
be a harmonic morphism of weighted graphs (G
′, g
′) and (G, g). We define the ramification degree of f at a vertex
![]() $v\in V(G')$
to be the quantity
$v\in V(G')$
to be the quantity
We say that f is unramified if it satisfies the local Riemann–Hurwitz condition
![]() $\textrm{Ram}_f(v')=0$
for all
$\textrm{Ram}_f(v')=0$
for all
![]() $v'\in V(G')$
, where we note that, in contrast to the algebraic setting, it is possible for the ramification degree at a vertex to be negative. A harmonic morphism
$v'\in V(G')$
, where we note that, in contrast to the algebraic setting, it is possible for the ramification degree at a vertex to be negative. A harmonic morphism
![]() $\phi\;:\;\Gamma'\to \Gamma$
of tropical curves is unramified if it has an unramified model. Our definition of ramification was introduced in [
Reference Ulirsch and ZakharovUZ19
], and is equivalent to the standard definition found in [
Reference Amini, Baker, Brugallé and RabinoffABBR15a
] or [
Reference Cavalieri, Markwig and RanganathanCMR16
].
$\phi\;:\;\Gamma'\to \Gamma$
of tropical curves is unramified if it has an unramified model. Our definition of ramification was introduced in [
Reference Ulirsch and ZakharovUZ19
], and is equivalent to the standard definition found in [
Reference Amini, Baker, Brugallé and RabinoffABBR15a
] or [
Reference Cavalieri, Markwig and RanganathanCMR16
].
2. Dilated cohomology and finite harmonic abelian covers
In this section, we give a cohomological classification of harmonic covers of a given metric graph with abelian structure group. For the remainder of this section, we fix a finite abelian group
![]() $\mathfrak{A}$
.
$\mathfrak{A}$
.
Let
![]() $\phi\colon \Gamma'\rightarrow \Gamma$
be a harmonic
$\phi\colon \Gamma'\rightarrow \Gamma$
be a harmonic
![]() $\mathfrak{A}$
-cover. For any point
$\mathfrak{A}$
-cover. For any point
![]() $p\in \Gamma$
, the stabiliser subgroups of any two points in the fiber
$p\in \Gamma$
, the stabiliser subgroups of any two points in the fiber
![]() $\phi^{-1}(p)$
are conjugate and hence equal. Therefore this group depends only on p, and we denote it by
$\phi^{-1}(p)$
are conjugate and hence equal. Therefore this group depends only on p, and we denote it by
![]() $D(p)\subseteq \mathfrak{A}$
and call it the dilation group of p. Similarly, choosing a finite graph model
$D(p)\subseteq \mathfrak{A}$
and call it the dilation group of p. Similarly, choosing a finite graph model
![]() $f\;:\;G'\to G$
of
$f\;:\;G'\to G$
of
![]() $\phi$
, we denote by
$\phi$
, we denote by
![]() $D(x)\subseteq \mathfrak{A}$
the stabiliser of any element of
$D(x)\subseteq \mathfrak{A}$
the stabiliser of any element of
![]() $f^{-1}(x)$
. The groups D(x) fulfil the semicontinuity property
$f^{-1}(x)$
. The groups D(x) fulfil the semicontinuity property
![]() $D(h)\subseteq D(v)$
for any half-edge
$D(h)\subseteq D(v)$
for any half-edge
![]() $h\in H(G)$
rooted at a vertex
$h\in H(G)$
rooted at a vertex
![]() $v\in V(G)$
. Furthermore, for any edge
$v\in V(G)$
. Furthermore, for any edge
![]() $e=\{h,h'\}\in E(G)$
we have
$e=\{h,h'\}\in E(G)$
we have
![]() $D(h)=D(h')$
, and we denote this group by D(e).
$D(h)=D(h')$
, and we denote this group by D(e).
This motivates the following definition.
Definition 2·1. An
![]() $\mathfrak{A}$
-dilation datum D on a finite graph G is a choice of a subgroup
$\mathfrak{A}$
-dilation datum D on a finite graph G is a choice of a subgroup
![]() $D(v)\subseteq \mathfrak{A}$
for every
$D(v)\subseteq \mathfrak{A}$
for every
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $D(h)\subseteq \mathfrak{A}$
for every
$D(h)\subseteq \mathfrak{A}$
for every
![]() $h\in H(G)$
, such that
$h\in H(G)$
, such that
![]() $D(h)\subset D(v)$
if h is rooted at v and such that
$D(h)\subset D(v)$
if h is rooted at v and such that
![]() $D(h)=D(h')=D(e)$
for any edge
$D(h)=D(h')=D(e)$
for any edge
![]() $e=\{h,h'\}\in E(G)$
. We note that if
$e=\{h,h'\}\in E(G)$
. We note that if
![]() $e\in E(G)$
is an edge with root vertices
$e\in E(G)$
is an edge with root vertices
![]() $u,v\in V(G)$
, then
$u,v\in V(G)$
, then
![]() $D(e)\subseteq D(u)\cap D(v)$
. An
$D(e)\subseteq D(u)\cap D(v)$
. An
![]() $\mathfrak{A}$
-dilation datum D on a metric graph
$\mathfrak{A}$
-dilation datum D on a metric graph
![]() $\Gamma$
is an
$\Gamma$
is an
![]() $\mathfrak{A}$
-dilation datum on some model G of
$\mathfrak{A}$
-dilation datum on some model G of
![]() $\Gamma$
, which defines a subgroup
$\Gamma$
, which defines a subgroup
![]() $D(p)\in \mathfrak{A}$
for each
$D(p)\in \mathfrak{A}$
for each
![]() $p\in \Gamma$
.
$p\in \Gamma$
.
An
![]() $\mathfrak{A}$
-dilation datum on a metric graph
$\mathfrak{A}$
-dilation datum on a metric graph
![]() $\Gamma$
together with a choice of simple model naturally gives rise to a dual sheaf of abelian groups.
$\Gamma$
together with a choice of simple model naturally gives rise to a dual sheaf of abelian groups.
Definition 2·2. Let D be an
![]() $\mathfrak{A}$
-dilation datum on a simple model G of a metric graph
$\mathfrak{A}$
-dilation datum on a simple model G of a metric graph
![]() $\Gamma$
. We define the codilation sheaf
$\Gamma$
. We define the codilation sheaf
![]() $\mathfrak{A}_D$
on
$\mathfrak{A}_D$
on
![]() $\Gamma$
as follows. For a vertex
$\Gamma$
as follows. For a vertex
![]() $v\in V(G)$
, we denote
$v\in V(G)$
, we denote
![]() $C(v)=D(v)$
. Similarly, for a leg
$C(v)=D(v)$
. Similarly, for a leg
![]() $l\in L(G)$
we denote
$l\in L(G)$
we denote
![]() $C(l)=D(v)$
, where
$C(l)=D(v)$
, where
![]() $v=r(l)$
. Finally, for an edge
$v=r(l)$
. Finally, for an edge
![]() $e\in E(G)$
with root vertices v and w, we denote
$e\in E(G)$
with root vertices v and w, we denote
![]() $C(e)=D(v)+D(w)\subseteq \mathfrak{A}$
. We note that
$C(e)=D(v)+D(w)\subseteq \mathfrak{A}$
. We note that
![]() $D(e)\subseteq C(e)$
for any edge
$D(e)\subseteq C(e)$
for any edge
![]() $e\in E(G)$
and
$e\in E(G)$
and
![]() $D(l)\subseteq C(l)$
for any leg
$D(l)\subseteq C(l)$
for any leg
![]() $l\in L(G)$
. Now let
$l\in L(G)$
. Now let
![]() $\mathcal{U}(G)=\{U_v,U_l\}$
be the star cover of
$\mathcal{U}(G)=\{U_v,U_l\}$
be the star cover of
![]() $\Gamma$
associated to G. The sections of
$\Gamma$
associated to G. The sections of
![]() $\mathfrak{A}_D$
over the open cover and the induced intersections are
$\mathfrak{A}_D$
over the open cover and the induced intersections are
where
![]() $U_e=U_v\cap U_w$
if e is the (unique) edge between v and w. The restriction maps are induced by the inclusions
$U_e=U_v\cap U_w$
if e is the (unique) edge between v and w. The restriction maps are induced by the inclusions
![]() $D(v)=C(v)\subseteq C(e)$
and
$D(v)=C(v)\subseteq C(e)$
and
![]() $D(v)=C(v)=C(l)$
for an edge e or a leg l rooted at a vertex v. Given a connected open set
$D(v)=C(v)=C(l)$
for an edge e or a leg l rooted at a vertex v. Given a connected open set
![]() $U\subseteq \Gamma$
, we set
$U\subseteq \Gamma$
, we set
![]() $\mathfrak{A}_D(U)=\mathfrak{A}_D(U_v)$
if
$\mathfrak{A}_D(U)=\mathfrak{A}_D(U_v)$
if
![]() $v\in U\subseteq U_v$
for some vertex v, while
$v\in U\subseteq U_v$
for some vertex v, while
![]() $\mathfrak{A}_D(U)=\mathfrak{A}_D(U_e)$
and
$\mathfrak{A}_D(U)=\mathfrak{A}_D(U_e)$
and
![]() $\mathfrak{A}_D(U)=\mathfrak{A}_D(U_l)$
respectively if
$\mathfrak{A}_D(U)=\mathfrak{A}_D(U_l)$
respectively if
![]() $U\subseteq U_e$
or
$U\subseteq U_e$
or
![]() $U\subseteq U_l$
. For larger open sets, we define the space of sections via the sheaf axioms.
$U\subseteq U_l$
. For larger open sets, we define the space of sections via the sheaf axioms.
The dilated cohomology group of the pair
![]() $(\Gamma,D)$
is the sheaf cohomology group
$(\Gamma,D)$
is the sheaf cohomology group
![]() $H^1(\Gamma,\mathfrak{A}_D)$
. We note that the sheaf
$H^1(\Gamma,\mathfrak{A}_D)$
. We note that the sheaf
![]() $\mathfrak{A}_D$
depends on the choice of model (see Example 2·4 below), but the group
$\mathfrak{A}_D$
depends on the choice of model (see Example 2·4 below), but the group
![]() $H^1(\Gamma,\mathfrak{A}_D)$
does not.
$H^1(\Gamma,\mathfrak{A}_D)$
does not.
We now show that harmonic
![]() $\mathfrak{A}$
-covers of
$\mathfrak{A}$
-covers of
![]() $\Gamma$
are in natural bijection with
$\Gamma$
are in natural bijection with
![]() $\mathfrak{A}_D$
-torsors. We first recall the definition of torsors over a sheaf of abelian groups, and their description in terms of Čech cocycles. Let
$\mathfrak{A}_D$
-torsors. We first recall the definition of torsors over a sheaf of abelian groups, and their description in terms of Čech cocycles. Let
![]() $\mathcal{F}$
be a sheaf of abelian groups on a topological space X. We may view
$\mathcal{F}$
be a sheaf of abelian groups on a topological space X. We may view
![]() $\mathcal{F}$
as a sheaf of
$\mathcal{F}$
as a sheaf of
![]() $\mathcal{F}$
-sets, with each group acting on itself by translation. An
$\mathcal{F}$
-sets, with each group acting on itself by translation. An
![]() $\mathcal{F}$
-torsor
$\mathcal{F}$
-torsor
![]() $\mathcal{T}$
on X is a locally trivial sheaf of
$\mathcal{T}$
on X is a locally trivial sheaf of
![]() $\mathcal{F}$
-sets, in other words a sheaf of
$\mathcal{F}$
-sets, in other words a sheaf of
![]() $\mathcal{F}$
-sets such that X admits a cover by open sets U with the property that
$\mathcal{F}$
-sets such that X admits a cover by open sets U with the property that
![]() $\mathcal{T}|_U$
and
$\mathcal{T}|_U$
and
![]() $\mathcal{F}|_U$
are isomorphic as sheaves of
$\mathcal{F}|_U$
are isomorphic as sheaves of
![]() $\mathcal{F}$
-sets.
$\mathcal{F}$
-sets.
It is wellknown that the set of isomorphism classes of
![]() $\mathcal{F}$
-torsors on X is the sheaf cohomology group
$\mathcal{F}$
-torsors on X is the sheaf cohomology group
![]() $H^1(X,\mathcal{F})$
. We explicitly calculate this group for a codilation sheaf
$H^1(X,\mathcal{F})$
. We explicitly calculate this group for a codilation sheaf
![]() $\mathfrak{A}_D$
on a metric graph
$\mathfrak{A}_D$
on a metric graph
![]() $\Gamma$
as a Čech cohomology group. Choose an oriented simple model G for
$\Gamma$
as a Čech cohomology group. Choose an oriented simple model G for
![]() $\Gamma$
, then the star cover
$\Gamma$
, then the star cover
![]() $\mathcal{U}(G)=\{U_v,U_l\}$
is acyclic for
$\mathcal{U}(G)=\{U_v,U_l\}$
is acyclic for
![]() $\mathfrak{A}_D$
. Let
$\mathfrak{A}_D$
. Let
![]() $\mathcal{T}$
be an
$\mathcal{T}$
be an
![]() $\mathfrak{A}_D$
-torsor, then we can find trivialisations
$\mathfrak{A}_D$
-torsor, then we can find trivialisations
![]() $g_v\;:\;\mathcal{T}|_{U_v}\to \mathfrak{A}_D|_{U_v}$
. Each edge
$g_v\;:\;\mathcal{T}|_{U_v}\to \mathfrak{A}_D|_{U_v}$
. Each edge
![]() $e\in E(G)$
corresponds to a nonempty intersection
$e\in E(G)$
corresponds to a nonempty intersection
![]() $U_e=U_{s(e)}\cap U_{t(e)}$
, and the composed isomorphism
$U_e=U_{s(e)}\cap U_{t(e)}$
, and the composed isomorphism
![]() $g^e=g_{t(e)}|_{U_e}\circ (g_{s(e)}|_{U_e})^{-1}\;:\;\mathfrak{A}|_{U_e}\to \mathfrak{A}|_{U_e}$
is given by translation by an element of
$g^e=g_{t(e)}|_{U_e}\circ (g_{s(e)}|_{U_e})^{-1}\;:\;\mathfrak{A}|_{U_e}\to \mathfrak{A}|_{U_e}$
is given by translation by an element of
![]() $\mathfrak{A}(U_e)=A/C(e)$
, which we also denote by
$\mathfrak{A}(U_e)=A/C(e)$
, which we also denote by
![]() $g^e$
. Hence the
$g^e$
. Hence the
![]() $\mathfrak{A}_D$
-torsor
$\mathfrak{A}_D$
-torsor
![]() $\mathcal{T}$
determines a tuple
$\mathcal{T}$
determines a tuple
![]() $(g^e)_{e\in E(G)}$
, where
$(g^e)_{e\in E(G)}$
, where
![]() $g^e\in A/C(e)$
. Choosing different trivialisations for
$g^e\in A/C(e)$
. Choosing different trivialisations for
![]() $\mathcal{T}$
over the sets
$\mathcal{T}$
over the sets
![]() $U_v$
determines a different tuple
$U_v$
determines a different tuple
![]() $(\tilde{g}^e)$
, and composing the trivialisations produces elements
$(\tilde{g}^e)$
, and composing the trivialisations produces elements
![]() $g^v\in \mathfrak{A}_D(U_v)=A/C(v)$
for
$g^v\in \mathfrak{A}_D(U_v)=A/C(v)$
for
![]() $v\in V(G)$
such that
$v\in V(G)$
such that
![]() $\tilde{g}^e-g^e=g^{t(e)}-g^{s(e)}$
in the common quotient group
$\tilde{g}^e-g^e=g^{t(e)}-g^{s(e)}$
in the common quotient group
![]() $\mathfrak{A}/C(e)$
. All triple intersections are empty, so the cocycle condition is trivially verified and the tuple
$\mathfrak{A}/C(e)$
. All triple intersections are empty, so the cocycle condition is trivially verified and the tuple
![]() $(g^e)$
determines an element of
$(g^e)$
determines an element of
![]() $\check{H}^1\big(\mathcal{U}(G),\mathfrak{A}_D\big)\cong H^1(\Gamma,\mathfrak{A}_D)$
, and we can reverse the construction to obtain
$\check{H}^1\big(\mathcal{U}(G),\mathfrak{A}_D\big)\cong H^1(\Gamma,\mathfrak{A}_D)$
, and we can reverse the construction to obtain
![]() $\mathcal{T}$
from
$\mathcal{T}$
from
![]() $(g^e)$
.
$(g^e)$
.
We now state our main result, which shows that harmonic
![]() $\mathfrak{A}$
-covers with fixed
$\mathfrak{A}$
-covers with fixed
![]() $\mathfrak{A}$
-dilation datum D are classified by the dilated cohomology group
$\mathfrak{A}$
-dilation datum D are classified by the dilated cohomology group
![]() $H^1(\Gamma,\mathfrak{A}_D)$
.
$H^1(\Gamma,\mathfrak{A}_D)$
.
Theorem 2·3.
Let
![]() $\Gamma$
be a metric graph and let D be an
$\Gamma$
be a metric graph and let D be an
![]() $\mathfrak{A}$
-dilation datum on
$\mathfrak{A}$
-dilation datum on
![]() $\Gamma$
. There is a natural one-to-one correspondence between
$\Gamma$
. There is a natural one-to-one correspondence between
![]() $\mathfrak{A}_D$
-torsors on
$\mathfrak{A}_D$
-torsors on
![]() $\Gamma$
and harmonic
$\Gamma$
and harmonic
![]() $\mathfrak{A}$
-covers of
$\mathfrak{A}$
-covers of
![]() $\Gamma$
with associated
$\Gamma$
with associated
![]() $\mathfrak{A}$
-dilation datum D.
$\mathfrak{A}$
-dilation datum D.
Proof. Choose an oriented simple model G for
![]() $\Gamma$
such that D is defined over G. Let
$\Gamma$
such that D is defined over G. Let
![]() $\phi\colon \Gamma'\rightarrow \Gamma$
be a harmonic
$\phi\colon \Gamma'\rightarrow \Gamma$
be a harmonic
![]() $\mathfrak{A}$
-cover with
$\mathfrak{A}$
-cover with
![]() $\mathfrak{A}$
-dilation datum D and let
$\mathfrak{A}$
-dilation datum D and let
![]() $f\;:\;G'\to G$
be a model for
$f\;:\;G'\to G$
be a model for
![]() $\phi$
. For any vertex
$\phi$
. For any vertex
![]() $v\in V(G)$
, the fiber
$v\in V(G)$
, the fiber
![]() $f^{-1}(v)$
is naturally a torsor over
$f^{-1}(v)$
is naturally a torsor over
![]() $\mathfrak{A}_D(U_v)=\mathfrak{A}/D(v)$
. The fiber
$\mathfrak{A}_D(U_v)=\mathfrak{A}/D(v)$
. The fiber
![]() $f^{-1}(e)$
over an edge e, however, is a torsor over
$f^{-1}(e)$
over an edge e, however, is a torsor over
![]() $\mathfrak{A}/D(e)$
, not over
$\mathfrak{A}/D(e)$
, not over
![]() $\mathfrak{A}_D(U_e)=\mathfrak{A}/C(e)$
. The latter group is a quotient of the former, and we replace
$\mathfrak{A}_D(U_e)=\mathfrak{A}/C(e)$
. The latter group is a quotient of the former, and we replace
![]() $f^{-1}(e)$
by its quotient by
$f^{-1}(e)$
by its quotient by
![]() $C(e)/D(e)$
. Similarly, for each leg
$C(e)/D(e)$
. Similarly, for each leg
![]() $l\in L(G)$
we take the quotient of
$l\in L(G)$
we take the quotient of
![]() $f^{-1}(l)$
by
$f^{-1}(l)$
by
![]() $C(l)/D(l)$
. In this way, we obtain an
$C(l)/D(l)$
. In this way, we obtain an
![]() $\mathfrak{A}_D$
-torsor on
$\mathfrak{A}_D$
-torsor on
![]() $\Gamma$
. We observe that, generally speaking, the espace étalé of this torsor is not Hausdorff, since if
$\Gamma$
. We observe that, generally speaking, the espace étalé of this torsor is not Hausdorff, since if
![]() $D(v)\subsetneq C(e)$
then the vertex v has more preimages than the adjacent edge e.
$D(v)\subsetneq C(e)$
then the vertex v has more preimages than the adjacent edge e.
Conversely, let
![]() $\mathcal{T}$
be an
$\mathcal{T}$
be an
![]() $\mathfrak{A}_D$
-torsor over
$\mathfrak{A}_D$
-torsor over
![]() $\Gamma$
. We construct a harmonic
$\Gamma$
. We construct a harmonic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $f\;:\;G'\to G$
by resolving the espace étalé of
$f\;:\;G'\to G$
by resolving the espace étalé of
![]() $\mathcal{T}$
in a canonical way. Let
$\mathcal{T}$
in a canonical way. Let
![]() $(g^e)\in \check{H}^1(\mathcal{U}(G),\mathfrak{A}_D)$
be a Čech cocycle representing
$(g^e)\in \check{H}^1(\mathcal{U}(G),\mathfrak{A}_D)$
be a Čech cocycle representing
![]() $\mathcal{T}$
. We arbitrarily lift each
$\mathcal{T}$
. We arbitrarily lift each
![]() $g^e\in A/C(e)$
to an element
$g^e\in A/C(e)$
to an element
![]() $\widetilde{g}^e\in\mathfrak{A}/D(e)$
. For each vertex
$\widetilde{g}^e\in\mathfrak{A}/D(e)$
. For each vertex
![]() $v\in V(G)$
, the fiber
$v\in V(G)$
, the fiber
![]() $f^{-1}(v)$
is equal to
$f^{-1}(v)$
is equal to
![]() $\mathfrak{A}/D(v)$
as an
$\mathfrak{A}/D(v)$
as an
![]() $\mathfrak{A}$
-set. For each edge
$\mathfrak{A}$
-set. For each edge
![]() $e\in V(G)$
with source and target vertices
$e\in V(G)$
with source and target vertices
![]() $v=s(e)$
and
$v=s(e)$
and
![]() $w=t(e)$
, the fiber
$w=t(e)$
, the fiber
![]() $f^{-1}(e)$
is
$f^{-1}(e)$
is
![]() $\mathfrak{A}/D(e)$
. The gluing map
$\mathfrak{A}/D(e)$
. The gluing map
![]() $f^{-1}(e)\to f^{-1}(v)$
is the natural quotient map
$f^{-1}(e)\to f^{-1}(v)$
is the natural quotient map
![]() $\mathfrak{A}/D(e)\to \mathfrak{A}/D(v)$
, while the gluing map
$\mathfrak{A}/D(e)\to \mathfrak{A}/D(v)$
, while the gluing map
![]() $f^{-1}(e)\to f^{-1}(w)$
is translation by
$f^{-1}(e)\to f^{-1}(w)$
is translation by
![]() $\widetilde{g}^e$
followed by taking the quotient. Finally, for each leg
$\widetilde{g}^e$
followed by taking the quotient. Finally, for each leg
![]() $l\in L(G)$
with root vertex v, we set
$l\in L(G)$
with root vertex v, we set
![]() $f^{-1}(l)=A/D(l)$
, and the root map
$f^{-1}(l)=A/D(l)$
, and the root map
![]() $f^{-1}(l)\to f^{-1}(v)$
is the quotient map
$f^{-1}(l)\to f^{-1}(v)$
is the quotient map
![]() $\mathfrak{A}/D(l)\to \mathfrak{A}/D(v)$
.
$\mathfrak{A}/D(l)\to \mathfrak{A}/D(v)$
.
One may now verify that these constructions are inverses of each other, thereby completing the proof.
Example 2·4. In the following picture, on the left, we illustrate a harmonic
![]() $\mathbb{Z}/4\mathbb{Z}$
-cover, for which the
$\mathbb{Z}/4\mathbb{Z}$
-cover, for which the
![]() $\mathbb{Z}/4\mathbb{Z}$
-dilation datum is given by
$\mathbb{Z}/4\mathbb{Z}$
-dilation datum is given by
![]() $D(u)=\mathbb{Z}/2\mathbb{Z}$
,
$D(u)=\mathbb{Z}/2\mathbb{Z}$
,
![]() $D(v)=\mathbb{Z}/4\mathbb{Z}$
, and
$D(v)=\mathbb{Z}/4\mathbb{Z}$
, and
![]() $D(e)=0$
. In this case we have
$D(e)=0$
. In this case we have
![]() $C(e)=\mathbb{Z}/4\mathbb{Z}$
and thus
$C(e)=\mathbb{Z}/4\mathbb{Z}$
and thus
![]() $(\mathfrak{A}_D)_u=\mathbb{Z}/2\mathbb{Z}$
,
$(\mathfrak{A}_D)_u=\mathbb{Z}/2\mathbb{Z}$
,
![]() $(\mathfrak{A}_D)_v=0$
, and
$(\mathfrak{A}_D)_v=0$
, and
![]() $(\mathfrak{A}_D)_e=0$
. The (non-Hausdorff) espace étalé of the associated
$(\mathfrak{A}_D)_e=0$
. The (non-Hausdorff) espace étalé of the associated
![]() $\mathcal{A}_D$
-torsor is illustrated on the right.
$\mathcal{A}_D$
-torsor is illustrated on the right.

Consider now a subdivision of the base with extra vertex w. Then the espace étalé of the associated codilation sheaf is given as follows:
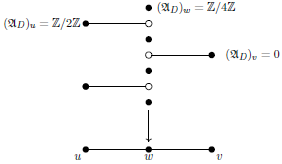
We point out that the dilated cohomology group
![]() $H^1(\Gamma,\mathfrak{A}_D)$
only depends on the dilation factors at vertices and not on the dilation factors along the edges. The interpretation of a class in
$H^1(\Gamma,\mathfrak{A}_D)$
only depends on the dilation factors at vertices and not on the dilation factors along the edges. The interpretation of a class in
![]() $H^1(\Gamma,\mathfrak{A}_D)$
in Proposition 2·3, however, does depend on the dilation along edges. That is, different choices of dilation factors would lead to different edge lengths in the corresponding harmonic covers.
$H^1(\Gamma,\mathfrak{A}_D)$
in Proposition 2·3, however, does depend on the dilation along edges. That is, different choices of dilation factors would lead to different edge lengths in the corresponding harmonic covers.
We now determine when a harmonic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $\phi\;:\;\Gamma'\to \Gamma$
of tropical curves is unramified. Let
$\phi\;:\;\Gamma'\to \Gamma$
of tropical curves is unramified. Let
![]() $f\;:\;G'\to G$
be a model of
$f\;:\;G'\to G$
be a model of
![]() $\phi$
, where G
′ and G are weighted graphs, and let
$\phi$
, where G
′ and G are weighted graphs, and let
![]() $v'\in V(G')$
be a vertex lying over
$v'\in V(G')$
be a vertex lying over
![]() $v=f(v')$
. The number of half-edges
$v=f(v')$
. The number of half-edges
![]() $h'\in T_{v'}(G')$
that are rooted at v
′ and that lie over a given half-edge
$h'\in T_{v'}(G')$
that are rooted at v
′ and that lie over a given half-edge
![]() $h\in T_vG$
is equal to the order of the corresponding quotient
$h\in T_vG$
is equal to the order of the corresponding quotient
![]() $\big|D(v)\big/D(h)\big|$
. A short calculation then shows that
$\big|D(v)\big/D(h)\big|$
. A short calculation then shows that
![]() $\textrm{Ram}_f(v')=0$
if and only if
$\textrm{Ram}_f(v')=0$
if and only if
 \begin{equation}g(v')=1+\big|D(v)\big|\big(g(v)-1\big)+\frac{\big|D(v)\big|}{2}\sum_{h\in T_vG}\left[1-\frac{1}{|D(h)|}\right].\end{equation}
\begin{equation}g(v')=1+\big|D(v)\big|\big(g(v)-1\big)+\frac{\big|D(v)\big|}{2}\sum_{h\in T_vG}\left[1-\frac{1}{|D(h)|}\right].\end{equation}
Since g(v) and g(v
′) are non-negative integers, this condition imposes certain restrictions on the
![]() $\mathfrak{A}$
-dilation datum of an unramified harmonic
$\mathfrak{A}$
-dilation datum of an unramified harmonic
![]() $\mathfrak{A}$
-cover. As an example, we consider the simplest case of a cyclic cover of prime order.
$\mathfrak{A}$
-cover. As an example, we consider the simplest case of a cyclic cover of prime order.
Example 2·5. Let
![]() $\phi\;:\;\Gamma'\to\Gamma$
be an unramified harmonic
$\phi\;:\;\Gamma'\to\Gamma$
be an unramified harmonic
![]() $\mathfrak{A}$
-cover of tropical curves with Galois group
$\mathfrak{A}$
-cover of tropical curves with Galois group
![]() $\mathfrak{A}=\mathbb{Z}/p\mathbb{Z}$
, where
$\mathfrak{A}=\mathbb{Z}/p\mathbb{Z}$
, where
![]() $p\geq 2$
is prime, and let
$p\geq 2$
is prime, and let
![]() $f\;:\;G'\to G$
be a model. For any element
$f\;:\;G'\to G$
be a model. For any element
![]() $x\in X(G)$
we have either
$x\in X(G)$
we have either
![]() $D(x)=\mathbb{Z}/p\mathbb{Z}$
or
$D(x)=\mathbb{Z}/p\mathbb{Z}$
or
![]() $D(x)=1$
, and we say that x is dilated or undilated, respectively. The set of dilated vertices and half-edges forms the dilation subgraph
$D(x)=1$
, and we say that x is dilated or undilated, respectively. The set of dilated vertices and half-edges forms the dilation subgraph
![]() $G_{\textrm{dil}}\subseteq G$
.
$G_{\textrm{dil}}\subseteq G$
.
Now let
![]() $v'\in V(G')$
be a vertex mapping to
$v'\in V(G')$
be a vertex mapping to
![]() $v=f(v')$
. If v is undilated, equation (5) simply reads
$v=f(v')$
. If v is undilated, equation (5) simply reads
![]() $g(v')=g(v)$
. For a dilated vertex
$g(v')=g(v)$
. For a dilated vertex
![]() $v\in V(G_{\textrm{dil}})$
, let
$v\in V(G_{\textrm{dil}})$
, let
![]() $d(v)=\big|\{h\in T_vG\mid D(h)=\mathbb{Z}/p\mathbb{Z}\}\big|$
be the valency of v in
$d(v)=\big|\{h\in T_vG\mid D(h)=\mathbb{Z}/p\mathbb{Z}\}\big|$
be the valency of v in
![]() $G_{\textrm{dil}}$
. Equation (5) then imposes the following conditions on g(v) and d(v):
$G_{\textrm{dil}}$
. Equation (5) then imposes the following conditions on g(v) and d(v):
-
(i) if
 $p=2$
, then
$p=2$
, then
 $d(v)\geq 2$
or
$d(v)\geq 2$
or
 $g(v)\geq 1$
, and in addition d(v) is even;
$g(v)\geq 1$
, and in addition d(v) is even; -
(ii) if
 $p\geq 3$
, then
$p\geq 3$
, then
 $d(v)\geq 2$
or
$d(v)\geq 2$
or
 $g(v)\geq 1$
.
$g(v)\geq 1$
.
In other words, the dilation subgraph
![]() $G_{\textrm{dil}}$
is semistable, and additionally if
$G_{\textrm{dil}}$
is semistable, and additionally if
![]() $p=2$
then each vertex of
$p=2$
then each vertex of
![]() $G_{\textrm{dil}}$
has even valency (see [
Reference Jensen and LenJL18
, lemma 5·4]).
$G_{\textrm{dil}}$
has even valency (see [
Reference Jensen and LenJL18
, lemma 5·4]).
3. Moduli of admissible
 $\mathfrak{G}$
-covers and their tropicalisation
$\mathfrak{G}$
-covers and their tropicalisation
Let
![]() $\mathfrak{\mathfrak{G}}$
be a fixed finite group, which, in this section, does not need to be abelian. In the following, we explain how harmonic
$\mathfrak{\mathfrak{G}}$
be a fixed finite group, which, in this section, does not need to be abelian. In the following, we explain how harmonic
![]() $\mathfrak{G}$
-covers of weighted graphs and tropical curves naturally arise as tropicalisations of algebraic
$\mathfrak{G}$
-covers of weighted graphs and tropical curves naturally arise as tropicalisations of algebraic
![]() $\mathfrak{G}$
-covers from a moduli-theoretic perspective, expanding on [
Reference Abramovich, Caporaso and PayneACP15
] and [
Reference Cavalieri, Markwig and RanganathanCMR16
] (recall that unramified harmonic morphisms of tropical curves are called tropical admissible covers in [
Reference Cavalieri, Markwig and RanganathanCMR16
]). We always work over
$\mathfrak{G}$
-covers from a moduli-theoretic perspective, expanding on [
Reference Abramovich, Caporaso and PayneACP15
] and [
Reference Cavalieri, Markwig and RanganathanCMR16
] (recall that unramified harmonic morphisms of tropical curves are called tropical admissible covers in [
Reference Cavalieri, Markwig and RanganathanCMR16
]). We always work over
![]() $\textrm{Spec} \mathbb{Z}\big[{1}/{\vert \mathfrak{G}\vert}\big]$
to avoid the wild world of non-tame covers.
$\textrm{Spec} \mathbb{Z}\big[{1}/{\vert \mathfrak{G}\vert}\big]$
to avoid the wild world of non-tame covers.
3·1. Compactifying the moduli space of
 $\mathfrak{G}$
-covers
$\mathfrak{G}$
-covers
Let
![]() $X\rightarrow S$
be a family of smooth projective curves of genus
$X\rightarrow S$
be a family of smooth projective curves of genus
![]() $g\geq 2$
with n marked disjoint sections
$g\geq 2$
with n marked disjoint sections
![]() $s_1,\ldots, s_n\in X(S)$
. A
$s_1,\ldots, s_n\in X(S)$
. A
![]() $\mathfrak{G}$
-cover of X is a finite morphism
$\mathfrak{G}$
-cover of X is a finite morphism
![]() $X'\rightarrow X$
together with an operation of
$X'\rightarrow X$
together with an operation of
![]() $\mathfrak{G}$
on X
′ over X that is a principal
$\mathfrak{G}$
on X
′ over X that is a principal
![]() $\mathfrak{G}$
-bundle on the complement of the sections, as well as a marking
$\mathfrak{G}$
-bundle on the complement of the sections, as well as a marking
![]() $s'_{ij}\in X'(S)$
of the disjoint preimages of the
$s'_{ij}\in X'(S)$
of the disjoint preimages of the
![]() $s_i$
, indexed by
$s_i$
, indexed by
![]() $i=1,\ldots, n$
and
$i=1,\ldots, n$
and
![]() $j=1,\ldots, k_i$
. Denote by
$j=1,\ldots, k_i$
. Denote by
![]() $\mathcal{H}_{g,\mathfrak{G}}$
the moduli space of connected
$\mathcal{H}_{g,\mathfrak{G}}$
the moduli space of connected
![]() $\mathfrak{G}$
-covers of smooth curves of genus g (see e.g. [
Reference Romagny and WewersRW06
] for a construction). There is a good notion of a limit object as X degenerates to a stable curve, as introduced in [
Reference Abramovich, Corti and VistoliACV03
].
$\mathfrak{G}$
-covers of smooth curves of genus g (see e.g. [
Reference Romagny and WewersRW06
] for a construction). There is a good notion of a limit object as X degenerates to a stable curve, as introduced in [
Reference Abramovich, Corti and VistoliACV03
].
Definition 3·1. Let
![]() $\mathfrak{G}$
be a finite group and let
$\mathfrak{G}$
be a finite group and let
![]() $X\rightarrow S$
be a family of stable curves of genus
$X\rightarrow S$
be a family of stable curves of genus
![]() $g\geq 0$
with n marked disjoint sections
$g\geq 0$
with n marked disjoint sections
![]() $s_1,\ldots, s_n$
. Let
$s_1,\ldots, s_n$
. Let
![]() $\mu=(r_1,\ldots, r_n)$
be an n-tuple of natural numbers that divide
$\mu=(r_1,\ldots, r_n)$
be an n-tuple of natural numbers that divide
![]() $|\mathfrak{G}|$
, and denote
$|\mathfrak{G}|$
, and denote
![]() $k_i=\vert\mathfrak{G}\vert/r_i$
for
$k_i=\vert\mathfrak{G}\vert/r_i$
for
![]() $i=1,\ldots, n$
. An admissible
$i=1,\ldots, n$
. An admissible
![]() $\mathfrak{G}$
-cover of X consists of a finite morphism
$\mathfrak{G}$
-cover of X consists of a finite morphism
![]() $X'\rightarrow X$
from a family of stable curves
$X'\rightarrow X$
from a family of stable curves
![]() $X'\rightarrow S$
, an action of
$X'\rightarrow S$
, an action of
![]() $\mathfrak{G}$
on X
′, and disjoint sections
$\mathfrak{G}$
on X
′, and disjoint sections
![]() $s'_{ij}$
of X
′ over S for
$s'_{ij}$
of X
′ over S for
![]() $i=1,\ldots,n$
and
$i=1,\ldots,n$
and
![]() $j=1,\ldots,k_i$
, subject to the following conditions:
$j=1,\ldots,k_i$
, subject to the following conditions:
-
(i) the morphism
 $X'\rightarrow X$
is a principal
$X'\rightarrow X$
is a principal
 $\mathfrak{G}$
-bundle away from the nodes and sections of X;
$\mathfrak{G}$
-bundle away from the nodes and sections of X; -
(ii) the preimage of the set of nodes in X is precisely the set of nodes of X ′;
-
(iii) the preimage of a section
 $s_i$
is precisely given by the sections
$s_i$
is precisely given by the sections
 $s'_{i1},\ldots, s'_{ik_i}$
;
$s'_{i1},\ldots, s'_{ik_i}$
; -
(iv) let p be a node in X and p ′ a node of X ′ above p. Then p ′ is étale-locally given by
 $x'y'=t$
for a suitable
$x'y'=t$
for a suitable
 $t\in\mathcal{O}_S$
and p is étale-locally given by
$t\in\mathcal{O}_S$
and p is étale-locally given by
 $xy=t^r$
for some integer
$xy=t^r$
for some integer
 $r\geq 1$
with
$r\geq 1$
with
 $(x')^r=x$
and
$(x')^r=x$
and
 $(y')^r=y$
, and the stabiliser of
$(y')^r=y$
, and the stabiliser of
 $\mathfrak{G}$
at p
′ is cyclic of order r and operates via for an rth root of unity
$\mathfrak{G}$
at p
′ is cyclic of order r and operates via for an rth root of unity \begin{equation*}(x',y')\longmapsto (\zeta x',\zeta^{-1} y')\end{equation*}
\begin{equation*}(x',y')\longmapsto (\zeta x',\zeta^{-1} y')\end{equation*}
 $\zeta\in\mu_r$
;
$\zeta\in\mu_r$
;
-
(v) étale-locally near the sections
 $s_i$
and
$s_i$
and
 $s'_{ij}$
, the morphism
$s'_{ij}$
, the morphism
 $X'\rightarrow X$
is given by
$X'\rightarrow X$
is given by
 $\mathcal{O}_S[t_i]\rightarrow \mathcal{O}_S[t'_{ij}]$
with
$\mathcal{O}_S[t_i]\rightarrow \mathcal{O}_S[t'_{ij}]$
with
 $(t'_{ij})^{r_i}=t_i$
for appropriate choices of
$(t'_{ij})^{r_i}=t_i$
for appropriate choices of
 $t_i$
and
$t_i$
and
 $t'_{ij}$
, and the stabiliser of
$t'_{ij}$
, and the stabiliser of
 $\mathfrak{G}$
along
$\mathfrak{G}$
along
 $s_{ij}$
is cyclic of order
$s_{ij}$
is cyclic of order
 $r_i$
and operates via
$r_i$
and operates via
 $t'_{ij}\mapsto \zeta t'_{ij}$
, for an
$t'_{ij}\mapsto \zeta t'_{ij}$
, for an
 $r_i$
th root of unity
$r_i$
th root of unity
 $\zeta\in \mu_{r_i}$
.
$\zeta\in \mu_{r_i}$
.
We emphasise that the
![]() $\mathfrak{G}$
-action is part of the data; so, in particular, an isomorphism between two admissible
$\mathfrak{G}$
-action is part of the data; so, in particular, an isomorphism between two admissible
![]() $\mathfrak{G}$
-covers has to be a
$\mathfrak{G}$
-covers has to be a
![]() $\mathfrak{G}$
-equivariant isomorphism. As explained in [
Reference Abramovich, Corti and VistoliACV03
], the moduli space
$\mathfrak{G}$
-equivariant isomorphism. As explained in [
Reference Abramovich, Corti and VistoliACV03
], the moduli space
![]() $\overline{\mathcal{H}}_{g,\mathfrak{G}}(\mu)$
of admissible
$\overline{\mathcal{H}}_{g,\mathfrak{G}}(\mu)$
of admissible
![]() $\mathfrak{G}$
-covers of stable n-marked curves of genus g is a smooth and proper Deligne–Mumford stack over
$\mathfrak{G}$
-covers of stable n-marked curves of genus g is a smooth and proper Deligne–Mumford stack over
![]() $\textrm{Spec} \mathbb{Z}[{1}/{\vert \mathfrak{G}\vert}]$
that contains the locus
$\textrm{Spec} \mathbb{Z}[{1}/{\vert \mathfrak{G}\vert}]$
that contains the locus
![]() $\mathcal{H}_{g,\mathfrak{G}}(\mu)$
of
$\mathcal{H}_{g,\mathfrak{G}}(\mu)$
of
![]() $\mathfrak{G}$
-covers of smooth curves of ramification type
$\mathfrak{G}$
-covers of smooth curves of ramification type
![]() $\mu$
as an open substack. The complement of
$\mu$
as an open substack. The complement of
![]() $\mathcal{H}_{g,\mathfrak{G}}(\mu)$
is a normal crossing divisor.
$\mathcal{H}_{g,\mathfrak{G}}(\mu)$
is a normal crossing divisor.
Remark 3·2. Although closely related, the moduli space
![]() $\overline{\mathcal{H}}_{g, \mathfrak{G}}(\mu)$
is actually not quite the same as the one constructed in [
Reference Abramovich, Corti and VistoliACV03
]. The quotient
$\overline{\mathcal{H}}_{g, \mathfrak{G}}(\mu)$
is actually not quite the same as the one constructed in [
Reference Abramovich, Corti and VistoliACV03
]. The quotient
which forgets about the order of the marked sections on
![]() $s'_{ij}$
of X
′ over S for
$s'_{ij}$
of X
′ over S for
![]() $i=1,\ldots,n$
and
$i=1,\ldots,n$
and
![]() $j=1,\ldots,k_i$
, is equivalent to a connected component of the moduli space of twisted stable maps to
$j=1,\ldots,k_i$
, is equivalent to a connected component of the moduli space of twisted stable maps to
![]() $\textbf{B}\mathfrak{G}$
in the sense of [
Reference Abramovich and VistoliAV02, Reference Abramovich, Corti and VistoliACV03
], indexed by ramification profile and decomposition into connected components. Our variant of this moduli space
$\textbf{B}\mathfrak{G}$
in the sense of [
Reference Abramovich and VistoliAV02, Reference Abramovich, Corti and VistoliACV03
], indexed by ramification profile and decomposition into connected components. Our variant of this moduli space
![]() $\overline{\mathcal{H}}_{g, \mathfrak{G}}(\mu)$
, with ordered sections on X
′, has also appeared in [
Reference Schmitt and van ZelmSvZ20
] and in [
Reference Jarvis, Kaufmann and KimuraJKK05
] (the latter permitting admissible covers with possibly disconnected domains).
$\overline{\mathcal{H}}_{g, \mathfrak{G}}(\mu)$
, with ordered sections on X
′, has also appeared in [
Reference Schmitt and van ZelmSvZ20
] and in [
Reference Jarvis, Kaufmann and KimuraJKK05
] (the latter permitting admissible covers with possibly disconnected domains).
An object in
![]() $\overline{\mathcal{H}}_{g, \mathfrak{G}}(\mu)$
is technically not an admissible
$\overline{\mathcal{H}}_{g, \mathfrak{G}}(\mu)$
is technically not an admissible
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $X'\rightarrow X$
but rather a
$X'\rightarrow X$
but rather a
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $X'\rightarrow \mathcal{X}$
of a twisted stable curve
$X'\rightarrow \mathcal{X}$
of a twisted stable curve
![]() $\mathcal{X}$
. A twisted stable curve
$\mathcal{X}$
. A twisted stable curve
![]() $\mathcal{X}\rightarrow S$
is a Deligne–Mumford stack
$\mathcal{X}\rightarrow S$
is a Deligne–Mumford stack
![]() $\mathcal{X}$
with sections
$\mathcal{X}$
with sections
![]() $s_1,\ldots, s_n\colon S\rightarrow \mathcal{X}$
whose coarse moduli space
$s_1,\ldots, s_n\colon S\rightarrow \mathcal{X}$
whose coarse moduli space
![]() $X\rightarrow S$
is a family of stable curves over S with n marked sections (also denoted by
$X\rightarrow S$
is a family of stable curves over S with n marked sections (also denoted by
![]() $s_1,\ldots, s_n$
) such that:
$s_1,\ldots, s_n$
) such that:
-
(1) the smooth locus of
 $\mathcal{X}$
is representable by a scheme;
$\mathcal{X}$
is representable by a scheme; -
(2) the singularities are étale-locally given by
 $\big[\{x'y'=t\}/\mu_r\big]$
for
$\big[\{x'y'=t\}/\mu_r\big]$
for
 $t\in\mathcal{O}_S$
, where
$t\in\mathcal{O}_S$
, where
 $\zeta\in\mu_r$
acts by
$\zeta\in\mu_r$
acts by
 $\zeta\cdot(x',y')=(\zeta x',\zeta^{-1}y')$
. In this case the singularity in X
′ is locally given by
$\zeta\cdot(x',y')=(\zeta x',\zeta^{-1}y')$
. In this case the singularity in X
′ is locally given by
 $xy=t^{r}$
;
$xy=t^{r}$
; -
(3) the stack
 $\mathcal{X}$
is a root stack
$\mathcal{X}$
is a root stack
 $\big[\sqrt[r_i]{s_i/X}\big]$
along the section
$\big[\sqrt[r_i]{s_i/X}\big]$
along the section
 $s_i$
for all
$s_i$
for all
 $i=1,\ldots, n$
;
$i=1,\ldots, n$
;
The two notions are naturally equivalent: given an admissible
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $X'\rightarrow X$
, the associated twisted
$X'\rightarrow X$
, the associated twisted
![]() $\mathfrak{G}$
-cover is given by
$\mathfrak{G}$
-cover is given by
![]() $X'\rightarrow [X'/\mathfrak{G}]$
. Conversely, given a twisted
$X'\rightarrow [X'/\mathfrak{G}]$
. Conversely, given a twisted
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $X'\rightarrow \mathcal{X}$
in the corresponding connected component, the composition
$X'\rightarrow \mathcal{X}$
in the corresponding connected component, the composition
![]() $X'\rightarrow\mathcal{X}\rightarrow X$
with the morphism to the coarse moduli space X is an admissible
$X'\rightarrow\mathcal{X}\rightarrow X$
with the morphism to the coarse moduli space X is an admissible
![]() $\mathfrak{G}$
-cover. We refer the interested reader to [
Reference Bertin and RomagnyBR11
] for an alternative construction.
$\mathfrak{G}$
-cover. We refer the interested reader to [
Reference Bertin and RomagnyBR11
] for an alternative construction.
3·2. From algebraic to tropical
 $\mathfrak{G}$
-covers
$\mathfrak{G}$
-covers
We now explain how to construct unramified harmonic
![]() $\mathfrak{G}$
-covers of weighted graphs and tropical curves from algebraic
$\mathfrak{G}$
-covers of weighted graphs and tropical curves from algebraic
![]() $\mathfrak{G}$
-covers.
$\mathfrak{G}$
-covers.
Definition 3·3. Let
![]() $F_0\;:\;X'_{0}\to X_0$
be an admissible
$F_0\;:\;X'_{0}\to X_0$
be an admissible
![]() $\mathfrak{G}$
-cover of stable nodal curves over an algebraically closed field k with n smooth distinct marked points on
$\mathfrak{G}$
-cover of stable nodal curves over an algebraically closed field k with n smooth distinct marked points on
![]() $X_0$
. The dual harmonic
$X_0$
. The dual harmonic
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $f\;:\;G'\to G$
is defined as follows:
$f\;:\;G'\to G$
is defined as follows:
-
(1) the graph G is the dual graph of
 $X_0$
, namely the irreducible components of
$X_0$
, namely the irreducible components of
 $X_0$
correspond to the vertices of G, the nodes correspond to the edges, and the sections correspond to the legs. Similarly, G
′ is the dual graph of
$X_0$
correspond to the vertices of G, the nodes correspond to the edges, and the sections correspond to the legs. Similarly, G
′ is the dual graph of
 $X'_{0}$
;
$X'_{0}$
; -
(ii) the vertex weights
 $g\;:\;V(G'_0)\to \mathbb{Z}_{\geq 0}$
and
$g\;:\;V(G'_0)\to \mathbb{Z}_{\geq 0}$
and
 $g\;:\;V(G_0)\to \mathbb{Z}_{\geq 0}$
are the genera of the normalisations of the corresponding irreducible components;
$g\;:\;V(G_0)\to \mathbb{Z}_{\geq 0}$
are the genera of the normalisations of the corresponding irreducible components; -
(iii) the legs of
 $G_0$
are marked
$G_0$
are marked
 $l\colon \{1,\ldots n\}\simeq L(G_0)$
according to the full order of the marked points;
$l\colon \{1,\ldots n\}\simeq L(G_0)$
according to the full order of the marked points; -
(iv) the morphism
 $F_0\;:\;X'_{0}\to X_0$
sends components to components, which defines the morphism
$F_0\;:\;X'_{0}\to X_0$
sends components to components, which defines the morphism
 $f\;:\;V(G')\to V(G)$
on the vertices;
$f\;:\;V(G')\to V(G)$
on the vertices; -
(v) every node
 $p_{e'}$
of
$p_{e'}$
of
 $X'_{0}$
has a local equation
$X'_{0}$
has a local equation
 $x'y'=0$
, and maps to a node
$x'y'=0$
, and maps to a node
 $p_e$
of
$p_e$
of
 $X_0$
with local equation
$X_0$
with local equation
 $xy=0$
via
$xy=0$
via
 $(x')^r=x$
and
$(x')^r=x$
and
 $(y')^r=y$
. This defines the map on the half-edges, and
$(y')^r=y$
. This defines the map on the half-edges, and
 $r=d_f(e')$
gives the dilation factor;
$r=d_f(e')$
gives the dilation factor; -
(vi) let
 $u'_{ij}$
be a uniformiser at
$u'_{ij}$
be a uniformiser at
 $s'_{ij}$
on
$s'_{ij}$
on
 $X'_{0}$
. Locally near
$X'_{0}$
. Locally near
 $s'_{ij}$
, the morphism
$s'_{ij}$
, the morphism
 $F_0$
is given by
$F_0$
is given by
 $u'_{ij}=u_i^{r_i}$
for a choice of uniformiser
$u'_{ij}=u_i^{r_i}$
for a choice of uniformiser
 $u_i$
at
$u_i$
at
 $s_i$
. The dilation factor
$s_i$
. The dilation factor
 $d_f(l'_{ij})$
along the leg corresponding to
$d_f(l'_{ij})$
along the leg corresponding to
 $s'_{ij}$
is equal to
$s'_{ij}$
is equal to
 $r_i$
.
$r_i$
.
The operation of
![]() $\mathfrak{G}$
on
$\mathfrak{G}$
on
![]() $X'_{0}$
induces an operation of
$X'_{0}$
induces an operation of
![]() $\mathfrak{G}$
on G
′ for which the map
$\mathfrak{G}$
on G
′ for which the map
![]() $f\;:\;G'\rightarrow G$
is
$f\;:\;G'\rightarrow G$
is
![]() $\mathfrak{G}$
-invariant. By Definition 3·1 (iii) and (iv), the stabiliser of every edge
$\mathfrak{G}$
-invariant. By Definition 3·1 (iii) and (iv), the stabiliser of every edge
![]() $e'_i$
and of every leg
$e'_i$
and of every leg
![]() $l'_{ij}$
is a cyclic group of order
$l'_{ij}$
is a cyclic group of order
![]() $r_i$
and
$r_i$
and
![]() $r_{ij}$
, respectively. Since
$r_{ij}$
, respectively. Since
![]() $F_0\;:\;X'_{0}\rightarrow X_0$
is a principal
$F_0\;:\;X'_{0}\rightarrow X_0$
is a principal
![]() $\mathfrak{G}$
-bundle away from the nodes, the operation of
$\mathfrak{G}$
-bundle away from the nodes, the operation of
![]() $\mathfrak{G}$
on the fiber over each point in
$\mathfrak{G}$
on the fiber over each point in
![]() $X_0$
is transitive and so
$X_0$
is transitive and so
![]() $f\;:\;G'\rightarrow G$
is a harmonic
$f\;:\;G'\rightarrow G$
is a harmonic
![]() $\mathfrak{G}$
-cover. Applying the Riemann–Hurwitz formula to the restriction of
$\mathfrak{G}$
-cover. Applying the Riemann–Hurwitz formula to the restriction of
![]() $F_0$
to each irreducible component of
$F_0$
to each irreducible component of
![]() $X'_{0}$
, we observe that f is unramified.
$X'_{0}$
, we observe that f is unramified.
Definition 3·4. Let X be a smooth projective curve of genus g over a non-Archimedean field K (whose residue characteristic is zero or coprime to
![]() $\vert \mathfrak{G}\vert$
) with n marked points
$\vert \mathfrak{G}\vert$
) with n marked points
![]() $s_1,\ldots, s_n$
over K. Let
$s_1,\ldots, s_n$
over K. Let
![]() $(F\;:\;X'\rightarrow X,s'_{ij})$
be a
$(F\;:\;X'\rightarrow X,s'_{ij})$
be a
![]() $\mathfrak{G}$
-cover of X, where
$\mathfrak{G}$
-cover of X, where
![]() $i=1,\ldots,n$
and
$i=1,\ldots,n$
and
![]() $j=1,\ldots,k_i$
. By the valuative criterion for properness, applied to the stack
$j=1,\ldots,k_i$
. By the valuative criterion for properness, applied to the stack
![]() $\overline{\mathcal{H}}_{g,\mathfrak{G}}(\mu)$
, there is a finite extension L of K such that
$\overline{\mathcal{H}}_{g,\mathfrak{G}}(\mu)$
, there is a finite extension L of K such that
![]() $X'_L\rightarrow X_L$
extends to a family of admissible
$X'_L\rightarrow X_L$
extends to a family of admissible
![]() $\mathfrak{G}$
-covers
$\mathfrak{G}$
-covers
![]() $\mathcal{F}\;:\;\mathcal{X}'\rightarrow\mathcal{X}$
defined over the valuation ring R of L (with marked sections also denoted by
$\mathcal{F}\;:\;\mathcal{X}'\rightarrow\mathcal{X}$
defined over the valuation ring R of L (with marked sections also denoted by
![]() $s_i$
and
$s_i$
and
![]() $s'_{ij}$
). The dual harmonic
$s'_{ij}$
). The dual harmonic
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $\phi\;:\;\Gamma_{X'}\to \Gamma_X$
is defined as follows:
$\phi\;:\;\Gamma_{X'}\to \Gamma_X$
is defined as follows:
-
(1) the graph models of the tropical curves
 $\Gamma_{X'}$
and
$\Gamma_{X'}$
and
 $\Gamma_X$
are the dual graphs
$\Gamma_X$
are the dual graphs
 $G_{\mathcal{X}'}$
and
$G_{\mathcal{X}'}$
and
 $G_{\mathcal{X}}$
of the special fibers
$G_{\mathcal{X}}$
of the special fibers
 $\mathcal{X}'_0$
and
$\mathcal{X}'_0$
and
 $\mathcal{X}_0$
, respectively;
$\mathcal{X}_0$
, respectively; -
(2) the edge length function
 $\ell\colon E(G_{\mathcal{X}})\rightarrow\mathbb{R}_{>0}$
associates to an edge e the positive real number
$\ell\colon E(G_{\mathcal{X}})\rightarrow\mathbb{R}_{>0}$
associates to an edge e the positive real number
 $r\cdot\textrm{val}(t)$
, where the corresponding node of
$r\cdot\textrm{val}(t)$
, where the corresponding node of
 $\mathcal{X}$
is étale-locally given by an equation
$\mathcal{X}$
is étale-locally given by an equation
 $xy=t^r$
for
$xy=t^r$
for
 $t\in R$
. We similarly define the edge length function
$t\in R$
. We similarly define the edge length function
 $\ell\colon E(G_{\mathcal{X}'})\rightarrow\mathbb{R}_{>0}$
;
$\ell\colon E(G_{\mathcal{X}'})\rightarrow\mathbb{R}_{>0}$
; -
(3) the restriction
 $\mathcal{F}_0\;:\;\mathcal{X}'_0\to \mathcal{X}_0$
of
$\mathcal{F}_0\;:\;\mathcal{X}'_0\to \mathcal{X}_0$
of
 $\mathcal{F}$
to the special fibers is an admissible
$\mathcal{F}$
to the special fibers is an admissible
 $\mathfrak{G}$
-cover over k, and the underlying graph model for
$\mathfrak{G}$
-cover over k, and the underlying graph model for
 $\phi$
is the dual harmonic
$\phi$
is the dual harmonic
 $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
 $f\;:\;G_{\mathcal{X}'_0}\to G_{\mathcal{X}_0}$
of
$f\;:\;G_{\mathcal{X}'_0}\to G_{\mathcal{X}_0}$
of
 $\mathcal{F}_0$
.
$\mathcal{F}_0$
.
We note that the models
![]() $G_{\mathcal{X}'}$
and
$G_{\mathcal{X}'}$
and
![]() $G_{\mathcal{X}}$
depend on the choice of extension
$G_{\mathcal{X}}$
depend on the choice of extension
![]() $\mathcal{F}$
, but the tropical curves
$\mathcal{F}$
, but the tropical curves
![]() $\Gamma_{X'}$
and
$\Gamma_{X'}$
and
![]() $\Gamma_X$
do not.
$\Gamma_X$
do not.
The map
![]() $\phi\colon \Gamma_{X'}\rightarrow \Gamma_{X}$
may also seen to be harmonic by [
Reference Amini, Baker, Brugallé and RabinoffABBR15a
, theorem A] upon identifying
$\phi\colon \Gamma_{X'}\rightarrow \Gamma_{X}$
may also seen to be harmonic by [
Reference Amini, Baker, Brugallé and RabinoffABBR15a
, theorem A] upon identifying
![]() $\Gamma_{X'}$
and
$\Gamma_{X'}$
and
![]() $\Gamma_X$
with the non-Archimedean skeletons of
$\Gamma_X$
with the non-Archimedean skeletons of
![]() $(X')^{\textrm{an}}$
and
$(X')^{\textrm{an}}$
and
![]() $X^{\textrm{an}}$
, respectively. The morphism
$X^{\textrm{an}}$
, respectively. The morphism
![]() $\phi\;:\;\Gamma_{X'}\to \Gamma_X$
is unramified because f is unramified.
$\phi\;:\;\Gamma_{X'}\to \Gamma_X$
is unramified because f is unramified.
3·3. A modular perspective on tropicalisation
Following the recipe in [
Reference Cavalieri, Markwig and RanganathanCMR16
, section 3·2·3] one may construct a tropical moduli space
![]() $\mathcal{H}^{{\textrm{trop}}}_{g,\mathfrak{G}}(\mu)$
as a generalised cone complex that parametrises isomorphism classes of unramified harmonic
$\mathcal{H}^{{\textrm{trop}}}_{g,\mathfrak{G}}(\mu)$
as a generalised cone complex that parametrises isomorphism classes of unramified harmonic
![]() $\mathfrak{G}$
-covers with dilation type
$\mathfrak{G}$
-covers with dilation type
![]() $\mu$
along the marked legs.
$\mu$
along the marked legs.
Let us now work over an algebraically closed non-Archimedean field K, whose residue characteristic is either zero or coprime to
![]() $\vert \mathfrak{G}\vert$
. Denote by
$\vert \mathfrak{G}\vert$
. Denote by
![]() $\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
the Berkovich analytic spaceFootnote 1 associated to
$\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
the Berkovich analytic spaceFootnote 1 associated to
![]() $\mathcal{H}_{g,\mathfrak{G}}(\mu)$
. The process described in Section 3·2 above defines a natural tropicalisation map
$\mathcal{H}_{g,\mathfrak{G}}(\mu)$
. The process described in Section 3·2 above defines a natural tropicalisation map
 \begin{equation*}\begin{split}{\textrm{trop}}_{g,\mathfrak{G}}(\mu)\colon \mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)&\longrightarrow H_{g,\mathfrak{G}}^{{\textrm{trop}}}(\mu)\\\big[X'\rightarrow X,s_i,s'_{ij}\big]& \longmapsto \big[(\Gamma_{X'},g')\rightarrow(\Gamma_X,g)\big]\end{split}\end{equation*}
\begin{equation*}\begin{split}{\textrm{trop}}_{g,\mathfrak{G}}(\mu)\colon \mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)&\longrightarrow H_{g,\mathfrak{G}}^{{\textrm{trop}}}(\mu)\\\big[X'\rightarrow X,s_i,s'_{ij}\big]& \longmapsto \big[(\Gamma_{X'},g')\rightarrow(\Gamma_X,g)\big]\end{split}\end{equation*}
that associates to an admissible
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $X'\rightarrow X$
of smooth curves over a non-Archimedean extension L of K an unramified tropical
$X'\rightarrow X$
of smooth curves over a non-Archimedean extension L of K an unramified tropical
![]() $\mathfrak{G}$
-cover
$\mathfrak{G}$
-cover
![]() $\Gamma_{X'}\rightarrow \Gamma_X$
of the dual tropical curve
$\Gamma_{X'}\rightarrow \Gamma_X$
of the dual tropical curve
![]() $\Gamma_X$
of X.
$\Gamma_X$
of X.
Since the boundary of
![]() $\overline{\mathcal{H}}_{g,\mathfrak{G}}(\mu)$
has normal crossings, the open immersion
$\overline{\mathcal{H}}_{g,\mathfrak{G}}(\mu)$
has normal crossings, the open immersion
![]() $\mathcal{H}_{g,\mathfrak{G}}(\mu)\hookrightarrow \overline{\mathcal{H}}_{g,\mathfrak{G}}(\mu)$
is a toroidal embedding in the sense of [
Reference Kempf, Faye Knudsen, Mumford and Saint-DonatKKMSD73
]. Therefore, as explained in [
Reference Abramovich, Caporaso and PayneACP15, Reference ThuillierThu07, Reference UlirschUli21
], there is a natural strong deformation retraction
$\mathcal{H}_{g,\mathfrak{G}}(\mu)\hookrightarrow \overline{\mathcal{H}}_{g,\mathfrak{G}}(\mu)$
is a toroidal embedding in the sense of [
Reference Kempf, Faye Knudsen, Mumford and Saint-DonatKKMSD73
]. Therefore, as explained in [
Reference Abramovich, Caporaso and PayneACP15, Reference ThuillierThu07, Reference UlirschUli21
], there is a natural strong deformation retraction
![]() $\rho_{g,\mathfrak{G}}\colon \mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)\rightarrow \mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
onto a closed subset of
$\rho_{g,\mathfrak{G}}\colon \mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)\rightarrow \mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
onto a closed subset of
![]() $\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
that carries the structure of a generalised cone complex, the non-Archimedean skeleton
$\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
that carries the structure of a generalised cone complex, the non-Archimedean skeleton
![]() $\Sigma_{g,\mathfrak{G}}(\mu)$
of
$\Sigma_{g,\mathfrak{G}}(\mu)$
of
![]() $\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
. Expanding on [
Reference Cavalieri, Markwig and RanganathanCMR16
, theorem 1 and 4], we have:
$\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
. Expanding on [
Reference Cavalieri, Markwig and RanganathanCMR16
, theorem 1 and 4], we have:
Theorem 3·5.
The tropicalisation map
![]() ${\textit{trop}}_{g,\mathfrak{G}}(\mu)\colon\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)\longrightarrow H_{g,\mathfrak{G}}^{{\textit{trop}}}(\mu)$
factors through the retraction to the non-Archimedean skeleton
${\textit{trop}}_{g,\mathfrak{G}}(\mu)\colon\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)\longrightarrow H_{g,\mathfrak{G}}^{{\textit{trop}}}(\mu)$
factors through the retraction to the non-Archimedean skeleton
![]() $\Sigma_{g,\mathfrak{G}}(\mu)$
of
$\Sigma_{g,\mathfrak{G}}(\mu)$
of
![]() $\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
, so that the restriction
$\mathcal{H}_{g,\mathfrak{G}}^{\textrm{an}}(\mu)$
, so that the restriction
to the skeleton is a finite strict morphism of generalised cone complexes. Moreover, the diagram

commutes.
In other words, the restriction of
![]() ${\textrm{trop}}_{g,\mathfrak{G}}(\mu)$
onto a cone in
${\textrm{trop}}_{g,\mathfrak{G}}(\mu)$
onto a cone in
![]() $\Sigma_{g,\mathfrak{G}}(\mu)$
is an isomorphism onto a cone in
$\Sigma_{g,\mathfrak{G}}(\mu)$
is an isomorphism onto a cone in
![]() $H^{{\textrm{trop}}}_{g,\mathfrak{G}}(\mu)$
and every cone in
$H^{{\textrm{trop}}}_{g,\mathfrak{G}}(\mu)$
and every cone in
![]() $H_{g,\mathfrak{G}}^{{\textrm{trop}}}(\mu)$
has at most finitely many preimages in
$H_{g,\mathfrak{G}}^{{\textrm{trop}}}(\mu)$
has at most finitely many preimages in
![]() $\Sigma_{g,\mathfrak{G}}(\mu)$
. Theorem 3·5, in particular, implies that the tropicalisation map
$\Sigma_{g,\mathfrak{G}}(\mu)$
. Theorem 3·5, in particular, implies that the tropicalisation map
![]() ${\textrm{trop}}_{g,\mathfrak{G}}(\mu)$
is well-defined, continuous, and proper.
${\textrm{trop}}_{g,\mathfrak{G}}(\mu)$
is well-defined, continuous, and proper.
The proof is almost word for word the same as the one of [
Reference Cavalieri, Markwig and RanganathanCMR16
, theorems 1 and 4]. We need to observe that the construction in [
Reference Cavalieri, Markwig and RanganathanCMR16
] is compatible with the
![]() $\mathfrak{G}$
-operation on both the algebraic and the tropical side. Moreover, using [
Reference UlirschUli21
, section 4·5], one can extend the construction of a non-Archimedean skeleton from [
Reference Abramovich, Caporaso and PayneACP15, Reference ThuillierThu07
] to a possibly non-trivially valued base field K. We leave the details to the avid reader, since the statement of Theorem 3·5 is not strictly used in the remainder of this paper.
$\mathfrak{G}$
-operation on both the algebraic and the tropical side. Moreover, using [
Reference UlirschUli21
, section 4·5], one can extend the construction of a non-Archimedean skeleton from [
Reference Abramovich, Caporaso and PayneACP15, Reference ThuillierThu07
] to a possibly non-trivially valued base field K. We leave the details to the avid reader, since the statement of Theorem 3·5 is not strictly used in the remainder of this paper.
4. Realisability of abelian harmonic covers
In this section, we return to the abelian case and fix a finite abelian group
![]() $\mathfrak{A}$
. We show that the
$\mathfrak{A}$
. We show that the
![]() $\mathfrak{A}$
-dilation datum of a harmonic
$\mathfrak{A}$
-dilation datum of a harmonic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $\phi\;:\;\Gamma'\to \Gamma$
that is obtained by tropicalizing an algebraic
$\phi\;:\;\Gamma'\to \Gamma$
that is obtained by tropicalizing an algebraic
![]() $\mathfrak{A}$
-cover has a simple cohomological description. Conversely, we show that any harmonic
$\mathfrak{A}$
-cover has a simple cohomological description. Conversely, we show that any harmonic
![]() $\mathfrak{A}$
-cover whose
$\mathfrak{A}$
-cover whose
![]() $\mathfrak{A}$
-dilation datum admits such a description comes from an algebraic
$\mathfrak{A}$
-dilation datum admits such a description comes from an algebraic
![]() $\mathfrak{A}$
-cover. This gives us an elementary necessary condition for realisability (see Corollary 4·5), and other similar conditions can be readily found.
$\mathfrak{A}$
-cover. This gives us an elementary necessary condition for realisability (see Corollary 4·5), and other similar conditions can be readily found.
We begin by giving the definition of realisability for weighted graphs and for tropical curves.
Definition 4·1. Let k be an algebraically closed field.
-
(i) an unramified harmonic
 $\mathfrak{A}$
-cover of weighted graphs
$\mathfrak{A}$
-cover of weighted graphs
 $f\;:\;G'\to G$
is realisable over k if there exists an admissible
$f\;:\;G'\to G$
is realisable over k if there exists an admissible
 $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
 $X'_{0}\to X_0$
of stable nodal curves over k whose dual harmonic
$X'_{0}\to X_0$
of stable nodal curves over k whose dual harmonic
 $\mathfrak{A}$
-cover is f.
$\mathfrak{A}$
-cover is f. -
(ii) an unramified harmonic
 $\mathfrak{A}$
-cover of tropical curves
$\mathfrak{A}$
-cover of tropical curves
 $\phi\;:\;\Gamma'\to \Gamma$
is realisable over k if there exist a non-Archimedean field K whose residue field is k and a Galois
$\phi\;:\;\Gamma'\to \Gamma$
is realisable over k if there exist a non-Archimedean field K whose residue field is k and a Galois
 $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
 $F\;:\;X'\to X$
of smooth projective curves over K such that
$F\;:\;X'\to X$
of smooth projective curves over K such that
 $\phi$
is the tropicalisation of F.
$\phi$
is the tropicalisation of F.
4·1. From Galois covers to extended homology
Let K be a non-Archimedean field with valuation ring R and residue field k, whose characteristic p is either zero or coprime to
![]() $\vert \mathfrak{A}\vert$
. Let
$\vert \mathfrak{A}\vert$
. Let
![]() $F\colon X'\to X$
be a finite
$F\colon X'\to X$
be a finite
![]() $\mathfrak{A}$
-cover of smooth projective curves over K (where X
′ may be disconnected), which is ramified precisely at n
′ marked ramification points
$\mathfrak{A}$
-cover of smooth projective curves over K (where X
′ may be disconnected), which is ramified precisely at n
′ marked ramification points
![]() $p'_{1},\ldots, p'_{n'}\in X'$
over a collection of marked branch points
$p'_{1},\ldots, p'_{n'}\in X'$
over a collection of marked branch points
![]() $p_1,\ldots, p_n\in X$
. Let
$p_1,\ldots, p_n\in X$
. Let
![]() $\mathcal{F}\colon\mathcal{X}'\to \mathcal{X}$
be an extension of
$\mathcal{F}\colon\mathcal{X}'\to \mathcal{X}$
be an extension of
![]() $X'\to X$
to a family of admissible
$X'\to X$
to a family of admissible
![]() $\mathfrak{A}$
-covers over R (where we may have to replace K by a finite extension, as above). Let
$\mathfrak{A}$
-covers over R (where we may have to replace K by a finite extension, as above). Let
![]() $\phi\colon \Gamma_{X'}\rightarrow \Gamma_{X}$
be the induced tropical harmonic
$\phi\colon \Gamma_{X'}\rightarrow \Gamma_{X}$
be the induced tropical harmonic
![]() $\mathfrak{A}$
-cover with model
$\mathfrak{A}$
-cover with model
![]() $f\;:\;G_{\mathcal{X}'}\to G_{\mathcal{X}}$
(which depends on the choice of
$f\;:\;G_{\mathcal{X}'}\to G_{\mathcal{X}}$
(which depends on the choice of
![]() $\mathcal{F}$
extending F).
$\mathcal{F}$
extending F).
Let
![]() $v\in V(G_{\mathcal{X}})$
be a vertex, then the smooth locus
$v\in V(G_{\mathcal{X}})$
be a vertex, then the smooth locus
![]() $X^*_v$
of the irreducible component
$X^*_v$
of the irreducible component
![]() $X_v$
is a genus g(v) curve over k with
$X_v$
is a genus g(v) curve over k with
![]() $\textrm{val}(v)$
punctures. The
$\textrm{val}(v)$
punctures. The
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $\mathcal{F}^{-1}(X^*_v)\to X^*_v$
is determined by a monodromy representation
$\mathcal{F}^{-1}(X^*_v)\to X^*_v$
is determined by a monodromy representation
![]() $m_v\;:\;\pi_1^{{\acute{e}t}}(X^*_v,x_0)\to \mathfrak{A}$
. Since
$m_v\;:\;\pi_1^{{\acute{e}t}}(X^*_v,x_0)\to \mathfrak{A}$
. Since
![]() $\mathfrak{A}$
is abelian, the choice of base point is irrelevant, and the representation can be recorded by a tuple of elements of
$\mathfrak{A}$
is abelian, the choice of base point is irrelevant, and the representation can be recorded by a tuple of elements of
![]() $\mathfrak{A}$
in the following way. Let
$\mathfrak{A}$
in the following way. Let
 \begin{align*}& \Pi_{g(v),\textrm{val}(v)}\\[5pt] &=\big\langle \alpha_1,\ldots,\alpha_{g(v)},\beta_1\ldots,\beta_{g(v)},\gamma_1,\ldots,\gamma_{\textrm{val}(v)}\ \mid \ [\alpha_1,\beta_1]\cdots[\alpha_{g(v)},\beta_{g(v)}]\gamma_1\cdots\gamma_{\textrm{val}(v)}=1\big\rangle\end{align*}
\begin{align*}& \Pi_{g(v),\textrm{val}(v)}\\[5pt] &=\big\langle \alpha_1,\ldots,\alpha_{g(v)},\beta_1\ldots,\beta_{g(v)},\gamma_1,\ldots,\gamma_{\textrm{val}(v)}\ \mid \ [\alpha_1,\beta_1]\cdots[\alpha_{g(v)},\beta_{g(v)}]\gamma_1\cdots\gamma_{\textrm{val}(v)}=1\big\rangle\end{align*}
be the fundamental group of a genus g(v) Riemann surface with
![]() $\textrm{val}(v)$
punctures, where the
$\textrm{val}(v)$
punctures, where the
![]() $\gamma_j$
are small loops around the punctures. By a theorem of Grothendieck (see e.g. [
Reference SzamuelySza09
, theorem 4·9·1]), the étale fundamental group
$\gamma_j$
are small loops around the punctures. By a theorem of Grothendieck (see e.g. [
Reference SzamuelySza09
, theorem 4·9·1]), the étale fundamental group
![]() $\pi_1^{{\acute{e}t}}(X^*_v,x_0)$
is the profinite completion of
$\pi_1^{{\acute{e}t}}(X^*_v,x_0)$
is the profinite completion of
![]() $\Pi_{g(v),\textrm{val}(v)}$
when
$\Pi_{g(v),\textrm{val}(v)}$
when
![]() $p=0$
and the prime-to-p profinite completion of
$p=0$
and the prime-to-p profinite completion of
![]() $\Pi_{g(v),\textrm{val}(v)}$
when
$\Pi_{g(v),\textrm{val}(v)}$
when
![]() $p>0$
. Since
$p>0$
. Since
![]() $\vert \mathfrak{A}\vert$
is coprime to p, every continuous homomorphism
$\vert \mathfrak{A}\vert$
is coprime to p, every continuous homomorphism
![]() $\pi_1^{{\acute{e}t}}(X^*_v,x_0)\rightarrow \mathfrak{A}$
(where
$\pi_1^{{\acute{e}t}}(X^*_v,x_0)\rightarrow \mathfrak{A}$
(where
![]() $\mathfrak{A}$
is equipped with the discrete topology) is uniquely determined by a homomorphism
$\mathfrak{A}$
is equipped with the discrete topology) is uniquely determined by a homomorphism
![]() $\varphi\;:\;\Pi_{g(v),\textrm{val}(v)}\rightarrow \mathfrak{A}$
that factors as
$\varphi\;:\;\Pi_{g(v),\textrm{val}(v)}\rightarrow \mathfrak{A}$
that factors as
Hence the monodromy representation
![]() $m_v\colon \pi_1^{{\acute{e}t}}(X^*_v,x_0)\to \mathfrak{A}$
is uniquely determined by the images
$m_v\colon \pi_1^{{\acute{e}t}}(X^*_v,x_0)\to \mathfrak{A}$
is uniquely determined by the images
of the
![]() $\alpha_i$
and
$\alpha_i$
and
![]() $\beta_i$
, which may be arbitrary, as well as the images
$\beta_i$
, which may be arbitrary, as well as the images
where
![]() $h\in H(G_{\mathcal{X}})$
is the half-edge corresponding to the jth puncture on
$h\in H(G_{\mathcal{X}})$
is the half-edge corresponding to the jth puncture on
![]() $X_v$
. We note that
$X_v$
. We note that
![]() $\eta(h)$
acts by multiplication by a primitive rth root of unity in an étale neighbourhood of
$\eta(h)$
acts by multiplication by a primitive rth root of unity in an étale neighbourhood of
![]() $p_{h'}$
, where
$p_{h'}$
, where
![]() $r=d_{\phi}(h')$
. The unique relation in the group
$r=d_{\phi}(h')$
. The unique relation in the group
![]() $\Pi_{g(v),\textrm{val}(v)}$
implies that the elements
$\Pi_{g(v),\textrm{val}(v)}$
implies that the elements
![]() $\eta(h)$
satisfy
$\eta(h)$
satisfy
 \begin{align*} \sum_{j=1}^{\textrm{val}(v)}\varphi(\gamma_j)=\sum_{h\in T_vG_{\mathcal{X}}}\eta(h)=0.\end{align*}
\begin{align*} \sum_{j=1}^{\textrm{val}(v)}\varphi(\gamma_j)=\sum_{h\in T_vG_{\mathcal{X}}}\eta(h)=0.\end{align*}
Furthermore, for each pair of nodes
![]() $e=\{h,h'\}$
we have
$e=\{h,h'\}$
we have
![]() $\eta(h)+\eta(h')=0$
.
$\eta(h)+\eta(h')=0$
.
In other words, to an algebraic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $X'\to X$
we associate the following data on the graph
$X'\to X$
we associate the following data on the graph
![]() $G_{\mathcal{X}}$
:
$G_{\mathcal{X}}$
:
-
(1) an element
 $\eta(h)\in \mathfrak{A}$
for each
$\eta(h)\in \mathfrak{A}$
for each
 $h\in H(G_{\mathcal{X}})$
, so that
$h\in H(G_{\mathcal{X}})$
, so that
 $\eta(h)+\eta(h')=0$
for any edge
$\eta(h)+\eta(h')=0$
for any edge
 $e=\{h,h'\}$
in
$e=\{h,h'\}$
in
 $E(G_\mathcal{X})$
and
$E(G_\mathcal{X})$
and
 $\sum_{h\in T_v G_\mathcal{X}} \eta(h)=0$
for any vertex
$\sum_{h\in T_v G_\mathcal{X}} \eta(h)=0$
for any vertex
 $v\in V(G_\mathcal{X})$
;
$v\in V(G_\mathcal{X})$
; -
(2) an element
 $\xi(v)\in \mathfrak{A}^{2g(v)}$
for every vertex
$\xi(v)\in \mathfrak{A}^{2g(v)}$
for every vertex
 $v\in V(G_\mathcal{X})$
.
$v\in V(G_\mathcal{X})$
.
The collection of all
![]() $\eta(h)$
is nothing but a class
$\eta(h)$
is nothing but a class
![]() $\eta\in H_1(G_\mathcal{X},\mathfrak{A})$
in the simplicial homology of the graph
$\eta\in H_1(G_\mathcal{X},\mathfrak{A})$
in the simplicial homology of the graph
![]() $G_{\mathcal{X}}$
with coefficients in
$G_{\mathcal{X}}$
with coefficients in
![]() $\mathfrak{A}$
. Similarly, each
$\mathfrak{A}$
. Similarly, each
![]() $\mathfrak{A}^{2g(v)}$
can be thought of as the simplicial homology group (with coefficients in
$\mathfrak{A}^{2g(v)}$
can be thought of as the simplicial homology group (with coefficients in
![]() $\mathfrak{A}$
) of an infinitesimal genus g(v) graph located at the vertex v. This motivates the following definition.
$\mathfrak{A}$
) of an infinitesimal genus g(v) graph located at the vertex v. This motivates the following definition.
Definition 4·2. Let (G,g) be a weighted graph. The extended homology group of G with coefficients in
![]() $\mathfrak{A}$
is the finite abelian group
$\mathfrak{A}$
is the finite abelian group
Given a harmonic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $f\;:\;G_{\mathcal{X}'}\to G_{\mathcal{X}}$
of weighted graphs that is the tropicalisation of an algebraic
$f\;:\;G_{\mathcal{X}'}\to G_{\mathcal{X}}$
of weighted graphs that is the tropicalisation of an algebraic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $F\;:\;X'\to X$
, the datum
$F\;:\;X'\to X$
, the datum
![]() $(\eta,\xi)\in H_1^{\textrm{ext}}(G_{\mathcal{X}},\mathfrak{A})$
defined above is called the
$(\eta,\xi)\in H_1^{\textrm{ext}}(G_{\mathcal{X}},\mathfrak{A})$
defined above is called the
![]() $\mathfrak{A}$
-monodromy datum associated to the cover.
$\mathfrak{A}$
-monodromy datum associated to the cover.
We note that if
![]() $|\mathfrak{A}|$
is coprime to p, then the group of continuous homomorphisms from
$|\mathfrak{A}|$
is coprime to p, then the group of continuous homomorphisms from
![]() $\pi_1^{{\acute{e}t}}(X,x)$
to
$\pi_1^{{\acute{e}t}}(X,x)$
to
![]() $\mathfrak{A}$
is naturally identified with
$\mathfrak{A}$
is naturally identified with
![]() $H^1_{{\acute{e}t}}(X,\mathfrak{A})$
(see [
Reference MilneMil13
, example 11·3]), and hence the discussion above provides us with a natural homomorphism
$H^1_{{\acute{e}t}}(X,\mathfrak{A})$
(see [
Reference MilneMil13
, example 11·3]), and hence the discussion above provides us with a natural homomorphism
Note that we pass from cohomology to homology, as
![]() $G_{\mathcal{X}}$
is the dual graph of the special fiber
$G_{\mathcal{X}}$
is the dual graph of the special fiber
![]() $\mathcal{X}_0$
.
$\mathcal{X}_0$
.
4·2. Extended homology, dilation and realisability
We now observe that the
![]() $\mathfrak{A}$
-dilation datum of a harmonic
$\mathfrak{A}$
-dilation datum of a harmonic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $f\;:\;G_{\mathcal{X}'}\to G_{\mathcal{X}}$
obtained by tropicalising an algebraic
$f\;:\;G_{\mathcal{X}'}\to G_{\mathcal{X}}$
obtained by tropicalising an algebraic
![]() $\mathfrak{A}$
-cover can be read off from the
$\mathfrak{A}$
-cover can be read off from the
![]() $\mathfrak{A}$
-monodromy datum
$\mathfrak{A}$
-monodromy datum
![]() $(\eta,\xi)$
. Indeed, let
$(\eta,\xi)$
. Indeed, let
![]() $v'\in V(G_{\mathcal{X}'})$
be a vertex mapping to
$v'\in V(G_{\mathcal{X}'})$
be a vertex mapping to
![]() $v=f(v')$
. The restricted
$v=f(v')$
. The restricted
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $f^{-1}(X^*_v)\to X^*_v$
corresponds to the monodromy representation
$f^{-1}(X^*_v)\to X^*_v$
corresponds to the monodromy representation
![]() $m_v\;:\;\pi_1^{{\acute{e}t}}(X_v^*,x_0)\to \mathfrak{A}$
, so an element of
$m_v\;:\;\pi_1^{{\acute{e}t}}(X_v^*,x_0)\to \mathfrak{A}$
, so an element of
![]() $\mathfrak{A}$
preserves the irreducible component
$\mathfrak{A}$
preserves the irreducible component
![]() $X^*_{v'}\subseteq f^{-1}(X^*_v)$
(in other words, fixes v
′) if and only if it is in the image of
$X^*_{v'}\subseteq f^{-1}(X^*_v)$
(in other words, fixes v
′) if and only if it is in the image of
![]() $m_v$
, which is generated by the images of the
$m_v$
, which is generated by the images of the
![]() $\alpha_i$
,
$\alpha_i$
,
![]() $\beta_i$
, and
$\beta_i$
, and
![]() $\gamma_j$
. Similarly, the stabiliser of a node
$\gamma_j$
. Similarly, the stabiliser of a node
![]() $p_{h'}\in \mathcal{X}'_0$
mapping to
$p_{h'}\in \mathcal{X}'_0$
mapping to
![]() $p_h\in \mathcal{X}_0$
is generated by
$p_h\in \mathcal{X}_0$
is generated by
![]() $\eta(h)\in \mathfrak{A}$
. Hence we give the following definition.
$\eta(h)\in \mathfrak{A}$
. Hence we give the following definition.
Definition 4·3. Let (G,g) be a weighted graph, and let
![]() $(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
be an element of the extended homology group of G with coefficients in
$(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
be an element of the extended homology group of G with coefficients in
![]() $\mathfrak{A}$
. The associated
$\mathfrak{A}$
. The associated
![]() $\mathfrak{A}$
-dilation datum on G is defined as follows:
$\mathfrak{A}$
-dilation datum on G is defined as follows:
-
(i) for a half-edge
 $h\in H(G)$
, the dilation group D(h) is the cyclic subgroup of
$h\in H(G)$
, the dilation group D(h) is the cyclic subgroup of
 $\mathfrak{A}$
generated by the element
$\mathfrak{A}$
generated by the element
 $\eta(h)$
;
$\eta(h)$
; -
(ii) for a vertex
 $v\in V(G)$
, the dilation group D(v) is the subgroup of
$v\in V(G)$
, the dilation group D(v) is the subgroup of
 $\mathfrak{A}$
generated by
$\mathfrak{A}$
generated by
 $\eta(h)$
for all
$\eta(h)$
for all
 $h\in T_vG$
and by the entries of
$h\in T_vG$
and by the entries of
 $\xi(v)$
.
$\xi(v)$
.
We are now ready to state and prove our realisability criterion.
Theorem 4·4.
Let k be an algebraically closed field whose characteristic is either zero or is relatively prime to
![]() $|\mathfrak{A}|$
.
$|\mathfrak{A}|$
.
-
(i) an unramified harmonic
 $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
 $f\;:\;G'\to G$
of weighted graphs is realisable over k if and only if the
$f\;:\;G'\to G$
of weighted graphs is realisable over k if and only if the
 $\mathfrak{A}$
-dilation datum D of f is associated to some element
$\mathfrak{A}$
-dilation datum D of f is associated to some element
 $(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
of the extended homology group of G with coefficients in
$(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
of the extended homology group of G with coefficients in
 $\mathfrak{A}$
.
$\mathfrak{A}$
. -
(ii) an unramified harmonic
 $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
 $\phi\;:\;\Gamma'\to \Gamma$
of tropical curves is realisable over k if and only if it admits a realisable model
$\phi\;:\;\Gamma'\to \Gamma$
of tropical curves is realisable over k if and only if it admits a realisable model
 $f\;:\;G'\to G$
.
$f\;:\;G'\to G$
.
Proof. Let
![]() $F_0\;:\;X'_{0}\to X_0$
be an admissible
$F_0\;:\;X'_{0}\to X_0$
be an admissible
![]() $\mathfrak{A}$
-cover of stable nodal curves over k, and let
$\mathfrak{A}$
-cover of stable nodal curves over k, and let
![]() $f\;:\;G'\to G$
be the dual cover. The discussion in Section 4.1 produces an
$f\;:\;G'\to G$
be the dual cover. The discussion in Section 4.1 produces an
![]() $\mathfrak{A}$
-monodromy datum
$\mathfrak{A}$
-monodromy datum
![]() $(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
that defines the
$(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
that defines the
![]() $\mathfrak{A}$
-dilation datum of f. Similarly, let
$\mathfrak{A}$
-dilation datum of f. Similarly, let
![]() $F\;:\;X'\to X$
be a
$F\;:\;X'\to X$
be a
![]() $\mathfrak{G}$
-cover of smooth projective curves over a non-Archimedean field K with residue field k, then the dual cover
$\mathfrak{G}$
-cover of smooth projective curves over a non-Archimedean field K with residue field k, then the dual cover
![]() $\phi\;:\;\Gamma_{X'}\to \Gamma_X$
of tropical curves has a realisable model.
$\phi\;:\;\Gamma_{X'}\to \Gamma_X$
of tropical curves has a realisable model.
Conversely, suppose that the
![]() $\mathfrak{A}$
-dilation datum D of an unramified harmonic
$\mathfrak{A}$
-dilation datum D of an unramified harmonic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $f\;:\;G'\to G$
is associated to an element
$f\;:\;G'\to G$
is associated to an element
![]() $(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
. We reverse the procedure and construct an admissible
$(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
. We reverse the procedure and construct an admissible
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $F_0\;:\;X'_{0}\to X_0$
over k tropicalizing to f, as follows. For each vertex
$F_0\;:\;X'_{0}\to X_0$
over k tropicalizing to f, as follows. For each vertex
![]() $v\in V(G)$
, choose a smooth k-curve
$v\in V(G)$
, choose a smooth k-curve
![]() $X^*_v$
of genus g(v) with
$X^*_v$
of genus g(v) with
![]() $|T_vG|$
punctures. The monodromy element
$|T_vG|$
punctures. The monodromy element
![]() $(\eta,\xi)$
induces a monodromy representation
$(\eta,\xi)$
induces a monodromy representation
![]() $m_v\;:\;\pi_1^{{\acute{e}t}}(X^*_v,x_0)\to \mathfrak{A}$
at each
$m_v\;:\;\pi_1^{{\acute{e}t}}(X^*_v,x_0)\to \mathfrak{A}$
at each
![]() $v\in V(G)$
and hence an
$v\in V(G)$
and hence an
![]() $\mathfrak{A}$
-cover of each
$\mathfrak{A}$
-cover of each
![]() $X^*_v$
. We then glue these covers according to the incidence data of the graphs G’ and G to obtain an admissible
$X^*_v$
. We then glue these covers according to the incidence data of the graphs G’ and G to obtain an admissible
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $F_0\;:\;X'_{0}\to X_0$
, where the
$F_0\;:\;X'_{0}\to X_0$
, where the
![]() $X_v$
are the irreducible components of
$X_v$
are the irreducible components of
![]() $X_0$
. Hence f is realisable.
$X_0$
. Hence f is realisable.
If
![]() $f\;:\;G'\to G$
is the underlying model for a harmonic
$f\;:\;G'\to G$
is the underlying model for a harmonic
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $\phi\;:\;\Gamma'\to \Gamma$
, then the admissible
$\phi\;:\;\Gamma'\to \Gamma$
, then the admissible
![]() $\mathfrak{A}$
-cover
$\mathfrak{A}$
-cover
![]() $F_0\;:\;X'_{0}\to X_0$
can be smoothened to a family
$F_0\;:\;X'_{0}\to X_0$
can be smoothened to a family
![]() $\mathcal{F}\;:\;\mathcal{X}'\to \mathcal{X}$
by the smoothness of the moduli space of admissible
$\mathcal{F}\;:\;\mathcal{X}'\to \mathcal{X}$
by the smoothness of the moduli space of admissible
![]() $\mathfrak{A}$
-covers over
$\mathfrak{A}$
-covers over
![]() $\textrm{Spec} \mathbb{Z}[{1}/{\vert \mathfrak{A}\vert}]$
(see [
Reference Abramovich, Corti and VistoliACV03
, theorem 3·0·2]). Alternatively, one may also use the smoothening result for harmonic covers of metrised curve complexes from [
Reference Amini, Baker, Brugallé and RabinoffABBR15a
] and observe that their smoothing is compatible with group operations.
$\textrm{Spec} \mathbb{Z}[{1}/{\vert \mathfrak{A}\vert}]$
(see [
Reference Abramovich, Corti and VistoliACV03
, theorem 3·0·2]). Alternatively, one may also use the smoothening result for harmonic covers of metrised curve complexes from [
Reference Amini, Baker, Brugallé and RabinoffABBR15a
] and observe that their smoothing is compatible with group operations.
This criterion can be used to establish elementary graph-theoretic restrictions on realisable harmonic
![]() $\mathfrak{A}$
-covers. First, we note that if the dilation group of any half-edge is not cyclic, then the cover is not realisable. Now let G be a weighted graph with a bridge edge
$\mathfrak{A}$
-covers. First, we note that if the dilation group of any half-edge is not cyclic, then the cover is not realisable. Now let G be a weighted graph with a bridge edge
![]() $e\in E(G)$
. Any
$e\in E(G)$
. Any
![]() $\mathfrak{A}$
-monodromy datum
$\mathfrak{A}$
-monodromy datum
![]() $(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
vanishes on e, so the dilation group of any realisable
$(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
vanishes on e, so the dilation group of any realisable
![]() $\mathfrak{A}$
-cover is trivial along e. Hence we have established the following necessary condition for realisability.
$\mathfrak{A}$
-cover is trivial along e. Hence we have established the following necessary condition for realisability.
Corollary 4·5.
Let
![]() $\phi\colon \Gamma'\rightarrow\Gamma$
be a harmonic
$\phi\colon \Gamma'\rightarrow\Gamma$
be a harmonic
![]() $\mathfrak{A}$
-cover of metric graphs. If any bridge edge of
$\mathfrak{A}$
-cover of metric graphs. If any bridge edge of
![]() $\Gamma$
is dilated, then f is not realisable.
$\Gamma$
is dilated, then f is not realisable.
In the next section, we show that, for most simple abelian groups, this condition is in fact sufficient. Similarly, if G has a pair of parallel edges
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, then the dilation groups of any realisable
$e_2$
, then the dilation groups of any realisable
![]() $\mathfrak{A}$
-cover are equal on
$\mathfrak{A}$
-cover are equal on
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, since
$e_2$
, since
![]() $\eta(e_2)=\pm \eta(e_1)$
for any
$\eta(e_2)=\pm \eta(e_1)$
for any
![]() $(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
.
$(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathfrak{A})$
.
5. Cyclic covers and the nowhere-zero flow problem
In this section, we discuss unramified harmonic
![]() $\mathfrak{A}$
-covers of a weighted graph (G,g) without legs in the case where
$\mathfrak{A}$
-covers of a weighted graph (G,g) without legs in the case where
![]() $\mathfrak{A}=\mathbb{Z}/p\mathbb{Z}$
is a cyclic group of prime order. We show that the realisability problem for such covers is closely related to a classical problem in graph theory.
$\mathfrak{A}=\mathbb{Z}/p\mathbb{Z}$
is a cyclic group of prime order. We show that the realisability problem for such covers is closely related to a classical problem in graph theory.
Let G be a graph and let
![]() $n\geq 2$
. A nowhere-zero n-flow on G is an element
$n\geq 2$
. A nowhere-zero n-flow on G is an element
![]() $\eta\in H_1(G,\mathbb{Z}/n\mathbb{Z})$
such that
$\eta\in H_1(G,\mathbb{Z}/n\mathbb{Z})$
such that
![]() $\eta(e)\neq 0$
for all
$\eta(e)\neq 0$
for all
![]() $e\in E(G)$
. The problem is to determine sufficient conditions for the existence of a nowhere-zero n-flow on G. It is clear that G admits a nowhere-zero n-flow for any
$e\in E(G)$
. The problem is to determine sufficient conditions for the existence of a nowhere-zero n-flow on G. It is clear that G admits a nowhere-zero n-flow for any
![]() $n\geq 2$
only if G has no bridges, and that it admits a nowhere-zero 2-flow if and only if
$n\geq 2$
only if G has no bridges, and that it admits a nowhere-zero 2-flow if and only if
![]() $\textrm{val}(v)$
is even for all
$\textrm{val}(v)$
is even for all
![]() $v\in V(G)$
. On the other hand, Seymour’s 6-flow Theorem [
Reference SeymourSey81
] states that any bridgeless graph admits a nowhere-zero n-flow for
$v\in V(G)$
. On the other hand, Seymour’s 6-flow Theorem [
Reference SeymourSey81
] states that any bridgeless graph admits a nowhere-zero n-flow for
![]() $n=6$
, and it easily follows that this holds for any
$n=6$
, and it easily follows that this holds for any
![]() $n\geq 7$
as well. The intermediate cases
$n\geq 7$
as well. The intermediate cases
![]() $n=3$
, 4, and 5, however, are not currently known. Tutte’s conjecture states that every bridgeless graph has a nowhere-zero 5-flow [
Reference TutteTut54
, conjecture II].
$n=3$
, 4, and 5, however, are not currently known. Tutte’s conjecture states that every bridgeless graph has a nowhere-zero 5-flow [
Reference TutteTut54
, conjecture II].
Consider an unramified harmonic
![]() $\mathbb{Z}/p\mathbb{Z}$
-cover
$\mathbb{Z}/p\mathbb{Z}$
-cover
![]() $f\;:\;G'\to G$
of weighted graphs, where
$f\;:\;G'\to G$
of weighted graphs, where
![]() $p\geq 2$
is a prime number. Let
$p\geq 2$
is a prime number. Let
![]() $G_{\textrm{dil}}\subseteq G$
be the dilation subgraph, consisting of those vertices and half-edges whose dilation group is
$G_{\textrm{dil}}\subseteq G$
be the dilation subgraph, consisting of those vertices and half-edges whose dilation group is
![]() $\mathbb{Z}/p\mathbb{Z}$
. We now use the theory of nowhere-zero n-flows to show that the realisability of f is determined by the structure of
$\mathbb{Z}/p\mathbb{Z}$
. We now use the theory of nowhere-zero n-flows to show that the realisability of f is determined by the structure of
![]() $G_{\textrm{dil}}$
.
$G_{\textrm{dil}}$
.
Theorem 5·1.
Let p be a prime number, and let
![]() $f\;:\;G'\to G$
be an unramified harmonic
$f\;:\;G'\to G$
be an unramified harmonic
![]() $\mathbb{Z}/p\mathbb{Z}$
-cover of weighted graphs with no legs. If
$\mathbb{Z}/p\mathbb{Z}$
-cover of weighted graphs with no legs. If
![]() $p=2$
, then f is realisable. If
$p=2$
, then f is realisable. If
![]() $p\geq 7$
, then f is realisable if and only if the dilation subgraph
$p\geq 7$
, then f is realisable if and only if the dilation subgraph
![]() $G_{\textrm{dil}}\subseteq G$
has no bridges. If Tutte’s conjecture holds, the same is true for
$G_{\textrm{dil}}\subseteq G$
has no bridges. If Tutte’s conjecture holds, the same is true for
![]() $p=5$
.
$p=5$
.
Proof. We recall the results of Example 2·5. For
![]() $v\in V(G_{\textrm{dil}})$
, denote its valency in
$v\in V(G_{\textrm{dil}})$
, denote its valency in
![]() $G_{\textrm{dil}}$
by d(v). We showed that the dilation subgraph
$G_{\textrm{dil}}$
by d(v). We showed that the dilation subgraph
![]() $G_{\textrm{dil}}\subseteq G$
is semistable: for each
$G_{\textrm{dil}}\subseteq G$
is semistable: for each
![]() $v\in V(G_{\textrm{dil}})$
, either
$v\in V(G_{\textrm{dil}})$
, either
![]() $d(v)\geq 2$
or
$d(v)\geq 2$
or
![]() $g(v)\geq 1$
(in addition, d(v) is even if
$g(v)\geq 1$
(in addition, d(v) is even if
![]() $p=2$
). Unwrapping the definitions, Theorem 4·4 implies that the cover
$p=2$
). Unwrapping the definitions, Theorem 4·4 implies that the cover
![]() $f\;:\;G'\to G$
is realisable if and only if there exists an element
$f\;:\;G'\to G$
is realisable if and only if there exists an element
![]() $(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathbb{Z}/p\mathbb{Z})$
satisfying the following conditions:
$(\eta,\xi)\in H_1^{\textrm{ext}}(G,\mathbb{Z}/p\mathbb{Z})$
satisfying the following conditions:
-
(i)
 $\eta(e)\neq 0$
if and only if
$\eta(e)\neq 0$
if and only if
 $e\in E(G_{\textrm{dil}})$
;
$e\in E(G_{\textrm{dil}})$
; -
(ii) if
 $v\in V(G)$
is a vertex with no adjacent dilated edges, then
$v\in V(G)$
is a vertex with no adjacent dilated edges, then
 $v\in V(G_{\textrm{dil}})$
if and only if
$v\in V(G_{\textrm{dil}})$
if and only if
 $\xi(v)\neq 0$
.
$\xi(v)\neq 0$
.
The first condition is always satisfied when
![]() $p=2$
: setting
$p=2$
: setting
![]() $\eta(e)=1$
if and only if
$\eta(e)=1$
if and only if
![]() $e\in E(G_{\textrm{dil}})$
gives a cycle
$e\in E(G_{\textrm{dil}})$
gives a cycle
![]() $\eta\in H_1(G,\mathbb{Z}/2\mathbb{Z})$
, since d(v) is even for all
$\eta\in H_1(G,\mathbb{Z}/2\mathbb{Z})$
, since d(v) is even for all
![]() $v\in V(G_{\textrm{dil}})$
(see [
Reference Jensen and LenJL18
, lemma 5·9]). For
$v\in V(G_{\textrm{dil}})$
(see [
Reference Jensen and LenJL18
, lemma 5·9]). For
![]() $p\geq 7$
, Seymour’s theorem implies that we can find such an
$p\geq 7$
, Seymour’s theorem implies that we can find such an
![]() $\eta$
if and only if
$\eta$
if and only if
![]() $G_{\textrm{dil}}$
has no bridges, and Tutte’s conjecture implies the same for
$G_{\textrm{dil}}$
has no bridges, and Tutte’s conjecture implies the same for
![]() $p=5$
. The second condition, on the other hand, is trivially satisfied: if
$p=5$
. The second condition, on the other hand, is trivially satisfied: if
![]() $v\in V(G_{\textrm{dil}})$
is a dilated vertex with
$v\in V(G_{\textrm{dil}})$
is a dilated vertex with
![]() $d(v)=0$
, then
$d(v)=0$
, then
![]() $g(v)\geq 1$
and hence we can pick
$g(v)\geq 1$
and hence we can pick
![]() $\xi(v)$
to be any nontrivial element of
$\xi(v)$
to be any nontrivial element of
![]() $(\mathbb{Z}/p\mathbb{Z})^{2g(v)}$
, and similarly we can set
$(\mathbb{Z}/p\mathbb{Z})^{2g(v)}$
, and similarly we can set
![]() $\xi(v)=0$
for all
$\xi(v)=0$
for all
![]() $v\in V(G_{\textrm{dil}})\backslash V(G)$
. This completes the proof.
$v\in V(G_{\textrm{dil}})\backslash V(G)$
. This completes the proof.
We note that our results allow us to restate Tutte’s conjecture in a purely algebraic form. Let G be a bridgeless graph, and let
![]() $X_0$
be a nodal curve whose dual graph is G (over any algebraically closed field of characteristic not equal to 5). Suppose that
$X_0$
be a nodal curve whose dual graph is G (over any algebraically closed field of characteristic not equal to 5). Suppose that
![]() $X_0$
admits an admissible
$X_0$
admits an admissible
![]() $\mathbb{Z}/5\mathbb{Z}$
-cover
$\mathbb{Z}/5\mathbb{Z}$
-cover
![]() $X'_{0}\to X_0$
that is ramified at each node of
$X'_{0}\to X_0$
that is ramified at each node of
![]() $X_0$
. The dual harmonic
$X_0$
. The dual harmonic
![]() $\mathbb{Z}/5\mathbb{Z}$
-cover
$\mathbb{Z}/5\mathbb{Z}$
-cover
![]() $f\;:\;G'\to G$
has
$f\;:\;G'\to G$
has
![]() $G_{\textrm{dil}}=G$
, hence the
$G_{\textrm{dil}}=G$
, hence the
![]() $\mathbb{Z}/5\mathbb{Z}$
-monodromy datum
$\mathbb{Z}/5\mathbb{Z}$
-monodromy datum
![]() $(\eta,\xi)$
satisfies
$(\eta,\xi)$
satisfies
![]() $\eta(e)\neq 0$
for all
$\eta(e)\neq 0$
for all
![]() $e\in E(G)$
. Tutte’s conjecture is now equivalent to the following:
$e\in E(G)$
. Tutte’s conjecture is now equivalent to the following:
Conjecture 5·2.
Let k be an algebraically closed field with
![]() $\textrm{char} k\neq 5$
. Every nodal curve over k with no separating nodes has an admissible
$\textrm{char} k\neq 5$
. Every nodal curve over k with no separating nodes has an admissible
![]() $\mathbb{Z}/5\mathbb{Z}$
-cover that is ramified at each node.
$\mathbb{Z}/5\mathbb{Z}$
-cover that is ramified at each node.
Acknowledgements
The authors would like to thank Matthew Baker, Madeline Brandt, Renzo Cavalieri, Gavril Farkas, Paul Helminck, David Jensen, Andrew Obus, Sam Payne, Dhruv Ranganathan, Felix Röhrle, Matthew Satriano, Johannes Schmitt, Pedro Souza and Jason van Zelm for useful discussions. In addition, the authors thank the anonymous referee(s) for their helpful comments and suggestions.
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie–Skłodowska–Curie Grant Agreement No. 793039. ![]() M.U. has received funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) TRR 326 Geometry and Arithmetic of Uniformized Structures, project number 444845124, by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Sachbeihilfe From Riemann surfaces to tropical curves (and back again), project number 456557832, and from the LOEWE grant Uniformized Structures in Algebra and Geometry. Y.L. has received funding from the EPSRC New Investigator Award (grant number EP/X002004/1).
M.U. has received funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) TRR 326 Geometry and Arithmetic of Uniformized Structures, project number 444845124, by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Sachbeihilfe From Riemann surfaces to tropical curves (and back again), project number 456557832, and from the LOEWE grant Uniformized Structures in Algebra and Geometry. Y.L. has received funding from the EPSRC New Investigator Award (grant number EP/X002004/1).