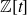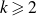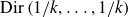Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
9 - Relativistic Field Theory
- from II - Part II
-
- Book:
- Condensed Matter Field Theory
- Published online:
- 24 August 2023
- Print publication:
- 14 September 2023, pp 522-571
-
- Chapter
- Export citation
II - Part II
-
- Book:
- Condensed Matter Field Theory
- Published online:
- 24 August 2023
- Print publication:
- 14 September 2023, pp 419-420
-
- Chapter
- Export citation
Contents
-
- Book:
- Condensed Matter Field Theory
- Published online:
- 24 August 2023
- Print publication:
- 14 September 2023, pp v-viii
-
- Chapter
- Export citation
3 - Path Integral
- from I - Part I
-
- Book:
- Condensed Matter Field Theory
- Published online:
- 24 August 2023
- Print publication:
- 14 September 2023, pp 91-170
-
- Chapter
- Export citation
Appendix D - Lorentz and Poincaré Groups
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 493-508
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp i-vi
-
- Chapter
- Export citation
10 - Electroweak Interaction
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 373-393
-
- Chapter
- Export citation
6 - A Brief Overview of Quantum Electrodynamics
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 167-223
-
- Chapter
- Export citation
12 - Nonequilibrium (Quantum)
- from II - Part II
-
- Book:
- Condensed Matter Field Theory
- Published online:
- 24 August 2023
- Print publication:
- 14 September 2023, pp 697-765
-
- Chapter
- Export citation
Dedication
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp v-vi
-
- Chapter
- Export citation
Preface
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp xv-xvii
-
- Chapter
- Export citation
Index
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 529-532
-
- Chapter
- Export citation
1 - Particle Physics Landscape
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 1-55
-
- Chapter
- Export citation
References
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 524-528
-
- Chapter
- Export citation
4 - Conservation Rules and Symmetries
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 101-116
-
- Chapter
- Export citation
8 - Topological Field Theory
- from II - Part II
-
- Book:
- Condensed Matter Field Theory
- Published online:
- 24 August 2023
- Print publication:
- 14 September 2023, pp 421-521
-
- Chapter
- Export citation
12 - The Standard Model and Beyond
-
- Book:
- Fundamentals of Particle Physics
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 432-459
-
- Chapter
- Export citation

Quantum Mechanics with Concept Maps
-
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023
-
- Textbook
- Export citation
Galois groups and prime divisors in random quadratic sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 95-122
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet law for factorisation of integers, polynomials and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 649-676
- Print publication:
- November 2023
-
- Article
- Export citation