Refine listing
Actions for selected content:
294 results in 14Hxx
Moduli spaces of stable quotients and wall-crossing phenomena
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. 1479-1518
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Gaudin subalgebras and stable rational curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1463-1478
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Braid monodromies on proper curves and pro-ℓ Galois representations
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 01 February 2011, pp. 161-188
- Print publication:
- January 2012
-
- Article
- Export citation
Modular compactifications of the space of pointed elliptic curves I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 877-913
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
The Mordell–Weil sieve: proving non-existence of rational points on curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 272-306
-
- Article
-
- You have access
- Export citation
The elliptic Hall algebra, Cherednik Hecke algebras and Macdonald polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 07 July 2010, pp. 188-234
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Quantum cohomology of [ℂN/μr]
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 1291-1322
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
FINITE GROUPS AS GALOIS GROUPS OF FUNCTION FIELDS WITH INFINITE FIELD OF CONSTANTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 14 May 2010, pp. 301-312
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Geometric realizations of the multiplihedra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 12 May 2010, pp. 1002-1028
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Explicit computations of Serre’s obstruction for genus-3 curves and application to optimal curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 192-207
-
- Article
-
- You have access
- Export citation
Automorphisms of hyperelliptic modular curves X0(N) in positive characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 April 2010, pp. 144-163
-
- Article
-
- You have access
- Export citation
Characteristic foliation on a hypersurface of general type in a projective symplectic manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 497-506
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Characteristic varieties and logarithmic differential 1-forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 129-144
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
Explicit Kummer surface formulas for arbitrary characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 January 2010, pp. 47-64
-
- Article
-
- You have access
- Export citation
Numerical criteria for divisors on
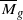 to be ample
to be ample
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 04 September 2009, pp. 1227-1248
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Harmonic and equianharmonic equations in the Grothendieck–Teichmüller group. III
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 431-448
- Print publication:
- April 2010
-
- Article
- Export citation
τ-function of discrete isomonodromy transformations and probability
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 747-772
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
VECTOR BUNDLES OVER A NONDEGENERATE CONIC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 145-154
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
ON THE INTERSECTION OF RATIONAL TRANSVERSAL SUBTORI
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 221-231
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
On the independence of the generators of tautological rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1497-1503
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
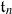 . We show that Gaudin subalgebras form a variety isomorphic to the moduli space
. We show that Gaudin subalgebras form a variety isomorphic to the moduli space 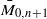 of stable curves of genus zero with
of stable curves of genus zero with 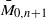 in a Grassmannian of (
in a Grassmannian of (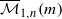 . We also consider weighted variants of these stability conditions, and construct the corresponding moduli stacks
. We also consider weighted variants of these stability conditions, and construct the corresponding moduli stacks 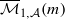 . In forthcoming work, we will prove that these stacks have projective coarse moduli and use the resulting spaces to give a complete description of the log minimal model program for
. In forthcoming work, we will prove that these stacks have projective coarse moduli and use the resulting spaces to give a complete description of the log minimal model program for 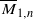 .
.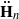 of type GL
of type GL . We prove a closed formula for the total Chern class of
. We prove a closed formula for the total Chern class of 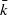 , being a Jacobian over
, being a Jacobian over  of a modular curve
of a modular curve 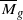 to be ample
to be ample
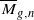 of
of 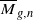
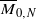 for
for 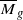 is known to be of general type.
is known to be of general type.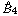 . A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.
. A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.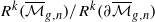 for all
for all 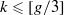 . We also give a simple argument for
. We also give a simple argument for 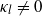 in
in  .
.