Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Smyth, David Ishii
2011.
Modular compactifications of the space of pointed elliptic curves II.
Compositio Mathematica,
Vol. 147,
Issue. 6,
p.
1843.
Smyth, David Ishii
2013.
Towards a classification of modular compactifications of $\mathcal {M}_{g,n}$.
Inventiones mathematicae,
Vol. 192,
Issue. 2,
p.
459.
Deopurkar, Anand
2013.
Modular compactifications of the space of marked trigonal curves.
Advances in Mathematics,
Vol. 248,
Issue. ,
p.
96.
Hall, Jack
2014.
A relative GAGA principle for families of curves.
Journal of the London Mathematical Society,
Vol. 90,
Issue. 1,
p.
29.
Alper, Jarod
Fedorchuk, Maksym
and
Smyth, David Ishii
2016.
Singularities with 𝔾
m
-action and\break the log minimal model program for ℳ¯
g
.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2016,
Issue. 721,
p.
1.
Pagani, Nicola
2016.
Moduli of abelian covers of elliptic curves.
Journal of Pure and Applied Algebra,
Vol. 220,
Issue. 3,
p.
1258.
Polishchuk, Alexander
2017.
Moduli of curves, Gröbner bases, and the Krichever map.
Advances in Mathematics,
Vol. 305,
Issue. ,
p.
682.
Lekili, Yankı
and
Polishchuk, Alexander
2017.
Arithmetic mirror symmetry for genus 1 curves with n marked points.
Selecta Mathematica,
Vol. 23,
Issue. 3,
p.
1851.
Polishchuk, Alexander
2017.
Moduli spaces of nonspecial pointed curves of arithmetic genus 1.
Mathematische Annalen,
Vol. 369,
Issue. 3-4,
p.
1021.
Alper, Jarod
Fedorchuk, Maksym
and
Smyth, David Ishii
2017.
Second flip in the Hassett–Keel program: existence of good moduli spaces.
Compositio Mathematica,
Vol. 153,
Issue. 8,
p.
1584.
Burban, Igor
and
Galinat, Lennart
2018.
Torsion Free Sheaves on Weierstrass Cubic Curves and the Classical Yang–Baxter Equation.
Communications in Mathematical Physics,
Vol. 364,
Issue. 1,
p.
123.
Aprodu, Marian
Farkas, Gavril
Papadima, Ştefan
Raicu, Claudiu
and
Weyman, Jerzy
2019.
Koszul modules and Green’s conjecture.
Inventiones mathematicae,
Vol. 218,
Issue. 3,
p.
657.
Ranganathan, Dhruv
Santos-Parker, Keli
and
Wise, Jonathan
2019.
Moduli of stable maps in genus one and logarithmic geometry, II.
Algebra & Number Theory,
Vol. 13,
Issue. 8,
p.
1765.
Lekili, Yankı
and
Polishchuk, Alexander
2019.
A modular compactification of ℳ1,n
from A
∞-structures.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 755,
p.
151.
Smyth, David
2019.
Intersections of 𝜓-classes on \overline{𝑀}_{1,𝑛}(𝑚).
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 12,
p.
8679.
Ranganathan, Dhruv
Santos-Parker, Keli
and
Wise, Jonathan
2019.
Moduli of stable maps in genus one and logarithmic geometry, I.
Geometry & Topology,
Vol. 23,
Issue. 7,
p.
3315.
Polishchuk, Alexander
2019.
MODULI OF CURVES WITH NONSPECIAL DIVISORS AND RELATIVE MODULI OF -STRUCTURES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 18,
Issue. 06,
p.
1295.
Battistella, Luca
Carocci, Francesca
and
Manolache, Cristina
2020.
Reduced invariants from cuspidal maps.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 9,
p.
6713.
Hamilton, Eloise
2020.
Classifying complete $$\mathbb {C}$$-subalgebras of $$\mathbb {C}[[t]]$$.
manuscripta mathematica,
Vol. 163,
Issue. 3-4,
p.
437.
Bozlee, Sebastian
2021.
Contractions of subcurves of families of log curves.
Communications in Algebra,
Vol. 49,
Issue. 11,
p.
4616.
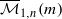 . We also consider weighted variants of these stability conditions, and construct the corresponding moduli stacks
. We also consider weighted variants of these stability conditions, and construct the corresponding moduli stacks 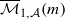 . In forthcoming work, we will prove that these stacks have projective coarse moduli and use the resulting spaces to give a complete description of the log minimal model program for
. In forthcoming work, we will prove that these stacks have projective coarse moduli and use the resulting spaces to give a complete description of the log minimal model program for 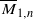 .
.
