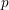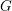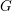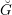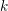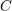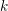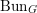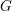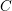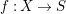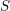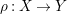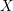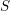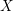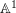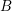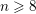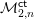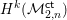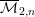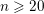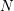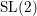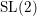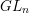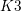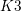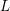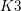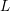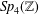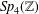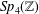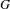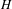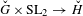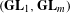Refine listing
Actions for selected content:
240 results in 14Dxx
HOMOGENEOUS SPACE FIBRATIONS OVER SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 03 April 2017, pp. 293-327
- Print publication:
- March 2019
-
- Article
- Export citation
OBSTRUCTION THEORY FOR SUPERMANIFOLDS AND DEFORMATIONS OF SUPERCONFORMAL STRUCTURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 15 March 2017, pp. 512-514
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
The Craighero–Gattazzo surface is simply connected
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 28 February 2017, pp. 557-585
- Print publication:
- March 2017
-
- Article
- Export citation
Geometric Langlands in prime characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 16 February 2017, pp. 395-452
- Print publication:
- February 2017
-
- Article
- Export citation
MIXED HODGE STRUCTURES OF THE MODULI SPACES OF PARABOLIC CONNECTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 225 / March 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 185-206
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
FAMILIES OF AFFINE RULED SURFACES: EXISTENCE OF CYLINDERS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 1-20
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
Tautological rings of spaces of pointed genus two curves of compact type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 17 June 2016, pp. 1398-1420
- Print publication:
- July 2016
-
- Article
- Export citation
MODULI SPACES OF RATIONAL WEIGHTED STABLE CURVES AND TROPICAL GEOMETRY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 03 June 2016, e9
-
- Article
-
- You have access
- Open access
- Export citation
The isotriviality of smooth families of canonically polarized manifolds over a special quasi-projective base
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1421-1434
- Print publication:
- July 2016
-
- Article
- Export citation
Failures of weak approximation in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1435-1475
- Print publication:
- July 2016
-
- Article
- Export citation
A finiteness theorem on symplectic singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1225-1236
- Print publication:
- June 2016
-
- Article
- Export citation
A BOUND ON EMBEDDING DIMENSIONS OF GEOMETRIC GENERIC FIBERS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 20 January 2016, e3
-
- Article
-
- You have access
- Open access
- Export citation
COMPACTIFICATIONS OF PEL-TYPE SHIMURA VARIETIES IN RAMIFIED CHARACTERISTICS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 05 January 2016, e1
-
- Article
-
- You have access
- Open access
- Export citation
Classification of horizontal
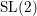 $\text{SL}(2)$s
$\text{SL}(2)$s
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 07 December 2015, pp. 918-954
- Print publication:
- May 2016
-
- Article
- Export citation
Logarithmic abelian varieties, Part IV: Proper models
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 9-63
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Compactifications of reductive groups as moduli stacks of bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 18 August 2015, pp. 62-98
- Print publication:
- January 2016
-
- Article
- Export citation
A Feynman integral via higher normal functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2329-2375
- Print publication:
- December 2015
-
- Article
- Export citation
SOME MONODROMY GROUPS OF FINITE INDEX IN
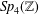 $\mathit{Sp}_{4}(\mathbb{Z})$
$\mathit{Sp}_{4}(\mathbb{Z})$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. 48-62
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Cohomology jump loci of differential graded Lie algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 1499-1528
- Print publication:
- August 2015
-
- Article
- Export citation
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 18 February 2015, pp. 625-671
- Print publication:
- July 2016
-
- Article
- Export citation