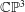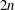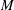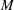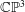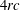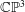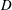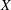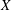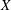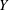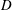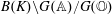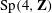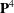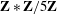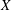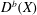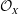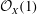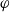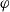Refine listing
Actions for selected content:
240 results in 14Dxx
ADHM CONSTRUCTION OF PERVERSE INSTANTON SHEAVES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 285-321
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
Représentations linéaires des groupes kählériens : factorisations et conjecture de Shafarevich linéaire
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 26 November 2014, pp. 351-376
- Print publication:
- February 2015
-
- Article
- Export citation
DERIVED LOGARITHMIC GEOMETRY I
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 28 October 2014, pp. 367-405
- Print publication:
- April 2016
-
- Article
- Export citation
Trihyperkähler reduction and instanton bundles on
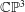 $\mathbb{C}\mathbb{P}^{3}$
$\mathbb{C}\mathbb{P}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1836-1868
- Print publication:
- November 2014
-
- Article
- Export citation
SUR LE COMPTAGE DES FIBRÉS DE HITCHIN NILPOTENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 August 2014, pp. 91-164
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
Stable maps and stable quotients
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1457-1481
- Print publication:
- September 2014
-
- Article
- Export citation
Laurent polynomials, GKZ-hypergeometric systems and mixed Hodge modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 24 April 2014, pp. 911-941
- Print publication:
- June 2014
-
- Article
- Export citation
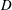 $D$-modules on spaces of rational maps
$D$-modules on spaces of rational maps
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 31 March 2014, pp. 835-876
- Print publication:
- May 2014
-
- Article
- Export citation
Thin monodromy in Sp(4)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 333-343
- Print publication:
- March 2014
-
- Article
- Export citation
Comptage des
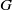 $G$-chtoucas: la partie elliptique
$G$-chtoucas: la partie elliptique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 2169-2183
- Print publication:
- December 2013
-
- Article
- Export citation
Moduli of products of stable varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 06 September 2013, pp. 2036-2070
- Print publication:
- December 2013
-
- Article
- Export citation
On the algebraicity of the zero locus of an admissible normal function
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 28 August 2013, pp. 1913-1962
- Print publication:
- November 2013
-
- Article
- Export citation
PARABOLIC HIGGS BUNDLES AND
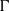 $\Gamma $-HIGGS BUNDLES
$\Gamma $-HIGGS BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 19 August 2013, pp. 315-328
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Families of canonically polarized manifolds over log Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 26 March 2013, pp. 1019-1040
- Print publication:
- June 2013
-
- Article
- Export citation
Computing zeta functions of nondegenerate hypersurfaces with few monomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 9-44
-
- Article
-
- You have access
- Export citation
Descendents on local curves: rationality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 01 November 2012, pp. 81-124
- Print publication:
- January 2013
-
- Article
- Export citation
Test configurations and Okounkov bodies
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 1736-1756
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
On arithmetic families of filtered
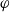 $\varphi $-modules and crystalline representations
$\varphi $-modules and crystalline representations
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 19 September 2012, pp. 677-726
- Print publication:
- October 2013
-
- Article
- Export citation
Hilbert schemes and Betti numbers over Clements–Lindström rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1337-1364
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Strictification of étale stacky Lie groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 807-834
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation