Refine search
Actions for selected content:
106116 results in Materials Science
Nomenclature
-
- Book:
- An Introduction to Composite Materials
- Published online:
- 04 July 2019
- Print publication:
- 11 July 2019, pp xiii-xvi
-
- Chapter
- Export citation
2019 ICDD Spring Meeting 11–15 March – ICDD® Headquarters
-
- Journal:
- Powder Diffraction / Volume 34 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 11 July 2019, pp. 198-202
-
- Article
- Export citation
5 - Elastic Deformation of Laminates
-
- Book:
- An Introduction to Composite Materials
- Published online:
- 04 July 2019
- Print publication:
- 11 July 2019, pp 67-76
-
- Chapter
- Export citation
9 - Fracture Mechanics and the Toughness of Composites
-
- Book:
- An Introduction to Composite Materials
- Published online:
- 04 July 2019
- Print publication:
- 11 July 2019, pp 142-177
-
- Chapter
- Export citation
PDJ volume 34 issue 2 Cover and Front matter
-
- Journal:
- Powder Diffraction / Volume 34 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 11 July 2019, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Calendar of Forthcoming Meetings
-
- Journal:
- Powder Diffraction / Volume 34 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 11 July 2019, pp. 211-212
-
- Article
-
- You have access
- HTML
- Export citation
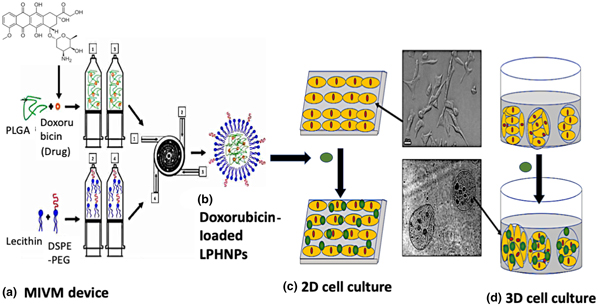
Improving the physiological relevance of drug testing for drug-loaded nanoparticles using 3D tumor cell cultures
-
- Journal:
- MRS Communications / Volume 9 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 1053-1059
- Print publication:
- September 2019
-
- Article
- Export citation
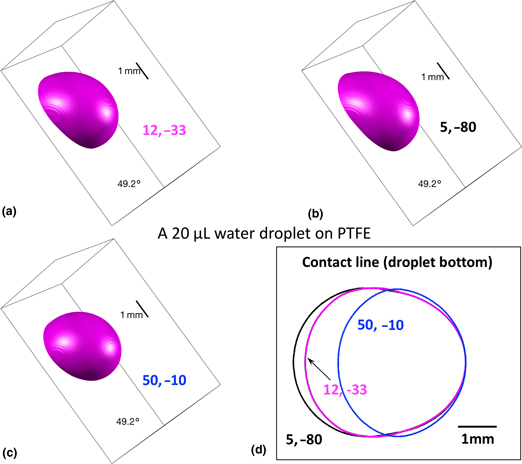
Simulating contact angle hysteresis using pseudo-line tensions
-
- Journal:
- MRS Communications / Volume 9 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 1060-1066
- Print publication:
- September 2019
-
- Article
- Export citation
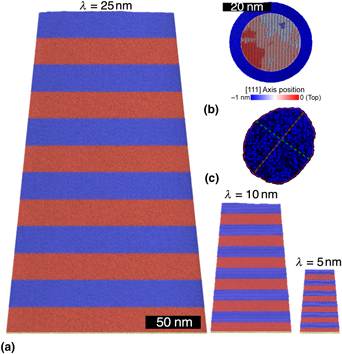
Surface flaws control strain localization in the deformation of Cu|Au nanolaminate pillars
-
- Journal:
- MRS Communications / Volume 9 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 1067-1071
- Print publication:
- September 2019
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
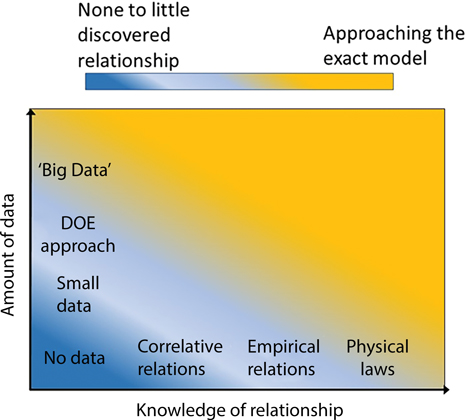
Embedding domain knowledge for machine learning of complex material systems
-
- Journal:
- MRS Communications / Volume 9 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 806-820
- Print publication:
- September 2019
-
- Article
- Export citation

An Introduction to Composite Materials
-
- Published online:
- 04 July 2019
- Print publication:
- 11 July 2019
-
- Textbook
- Export citation
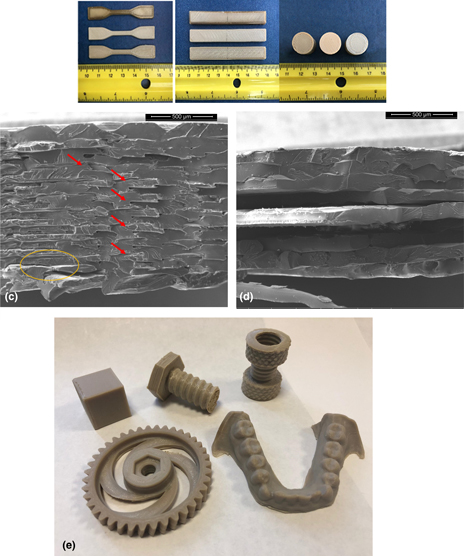
On the thermal processing and mechanical properties of 3D-printed polyether ether ketone
-
- Journal:
- MRS Communications / Volume 9 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 July 2019, pp. 1046-1052
- Print publication:
- September 2019
-
- Article
- Export citation
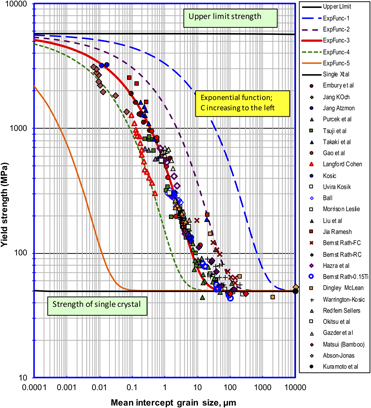
A new exponential function to represent the effect of grain size on the strength of pure iron over multiple length scales
-
- Journal:
- Journal of Materials Research / Volume 34 / Issue 13 / 15 July 2019
- Published online by Cambridge University Press:
- 03 July 2019, pp. 2315-2324
- Print publication:
- 15 July 2019
-
- Article
- Export citation
History of the reciprocal lattice
-
- Journal:
- Powder Diffraction / Volume 34 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 July 2019, pp. 260-266
-
- Article
- Export citation
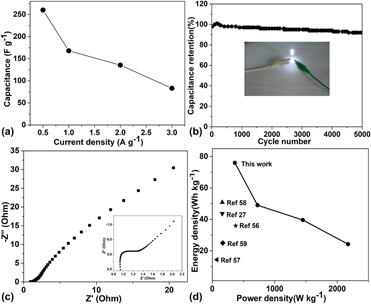
Hierarchical mesoporous Zn–Ni–Co–S microspheres grown on reduced graphene oxide/nickel foam for asymmetric supercapacitors
-
- Journal:
- Journal of Materials Research / Volume 34 / Issue 14 / 28 July 2019
- Published online by Cambridge University Press:
- 02 July 2019, pp. 2445-2455
- Print publication:
- 28 July 2019
-
- Article
- Export citation
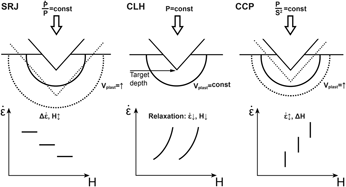
A new nanoindentation creep technique using constant contact pressure
-
- Journal:
- Journal of Materials Research / Volume 34 / Issue 14 / 28 July 2019
- Published online by Cambridge University Press:
- 02 July 2019, pp. 2492-2500
- Print publication:
- 28 July 2019
-
- Article
- Export citation
The machine learning revolution in materials?
-
- Journal:
- MRS Bulletin / Volume 44 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 530-537
- Print publication:
- July 2019
-
- Article
-
- You have access
- HTML
- Export citation
Commercializing colloidal quantum dot photovoltaics
-
- Journal:
- MRS Bulletin / Volume 44 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 524-525
- Print publication:
- July 2019
-
- Article
-
- You have access
- HTML
- Export citation
MRS volume 44 issue 7 Cover and Front matter
-
- Journal:
- MRS Bulletin / Volume 44 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. f1-f6
- Print publication:
- July 2019
-
- Article
-
- You have access
- Export citation
Engaging and inspiring MRS members
-
- Journal:
- MRS Bulletin / Volume 44 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 517-518
- Print publication:
- July 2019
-
- Article
-
- You have access
- HTML
- Export citation