Let $f(X) \in {\mathbb Z}[X]$ be a polynomial of degree $d \ge 2$ without multiple roots and let ${\mathcal F}(N)$ be the set of Farey fractions of order N. We use bounds for some new character sums and the square-sieve to obtain upper bounds, pointwise and on average, on the number of fields ${\mathbb Q}(\sqrt {f(r)})$ for $r\in {\mathcal F}(N)$, with a given discriminant.

We use bounds of character sums and some combinatorial arguments to show the abundance of very smooth numbers which also have very few nonzero binary digits.

We study the double character sum $\sum \limits _{\substack {m\leq X,\\m\mathrm {\ odd}}}\sum \limits _{\substack {n\leq Y,\\n\mathrm {\ odd}}}\left (\frac {m}{n}\right )$ and its smoothly weighted counterpart. An asymptotic formula with power saving error term was obtained by Conrey, Farmer, and Soundararajan by applying the Poisson summation formula. The result is interesting because the main term involves a non-smooth function. In this paper, we apply the inverse Mellin transform twice and study the resulting double integral that involves a double Dirichlet series. This method has two advantages—it leads to a better error term, and the surprising main term naturally arises from three residues of the double Dirichlet series.

This paper explores the existence and distribution of primitive elements in finite field extensions with prescribed traces in several intermediate field extensions. Our main result provides an inequality-like condition to ensure the existence of such elements. We then derive concrete existence results for a special class of intermediate extensions.

For any prime p, let $y(p)$ denote the smallest integer y such that every reduced residue class (mod p) is represented by the product of some subset of $\{1,\dots ,y\}$ . It is easy to see that $y(p)$ is at least as large as the smallest quadratic nonresidue (mod p); we prove that $y(p) \ll _\varepsilon p^{1/(4 \sqrt e)+\varepsilon }$ , thus strengthening Burgess’ classical result. This result is of intermediate strength between two other results, namely Burthe’s proof that the multiplicative group (mod p) is generated by the integers up to $O_\varepsilon (p^{1/(4 \sqrt e)+\varepsilon })$ , and Munsch and Shparlinski’s result that every reduced residue class (mod p) is represented by the product of some subset of the primes up to $O_\varepsilon (p^{1/(4 \sqrt e)+\varepsilon })$ . Unlike the latter result, our proof is elementary and similar in structure to Burgess’ proof for the least quadratic nonresidue.

In this paper, we obtain a variation of the Pólya–Vinogradov inequality with the sum restricted to a certain height. Assume $\chi $ to be a primitive character modulo q, $ \epsilon>0$ and $N\le q^{1-\gamma }$ , with $0\le \gamma \le 1/3$ . We prove that

$$ \begin{align*} |\sum_{n=1}^N \chi(n) |\le c (\tfrac{1}{3} -\gamma+\epsilon )\sqrt{q}\log q \end{align*} $$

$c=2/\pi ^2$

$\chi $

$c=1/\pi $

$\chi $

We prove character sum estimates for additive Bohr subsets modulo a prime. These estimates are analogous to the classical character sum bounds of Pólya–Vinogradov and Burgess. These estimates are applied to obtain results on recurrence $\bmod \,p$ by special elements.

We prove a subconvexity bound for the central value $L(\frac{1}{2},{\it\chi})$ of a Dirichlet 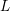$L$-function of a character ${\it\chi}$ to a prime power modulus $q=p^{n}$ of the form $L(\frac{1}{2},{\it\chi})\ll p^{r}q^{{\it\theta}+{\it\epsilon}}$ with a fixed $r$ and ${\it\theta}\approx 0.1645<\frac{1}{6}$, breaking the long-standing Weyl exponent barrier. In fact, we develop a general new theory of estimation of short exponential sums involving $p$-adically analytic phases, which can be naturally seen as a $p$-adic analogue of the method of exponent pairs. This new method is presented in a ready-to-use form and applies to a wide class of well-behaved phases including many that arise from a stationary phase analysis of hyper-Kloosterman and other complete exponential sums.

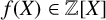
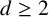
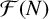
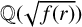
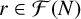
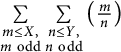
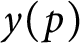
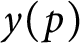
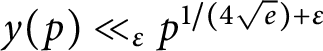
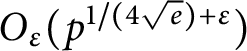
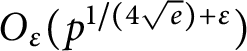
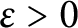
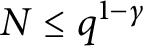
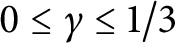
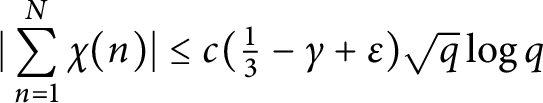
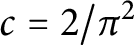
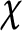
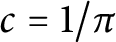
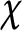
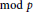
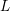
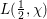
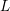
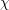
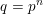
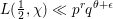
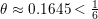
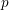
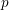
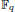Given a finite field of q elements, we consider a trajectory of the map 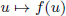associated with a polynomial 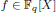]. Using bounds of character sums, under some mild condition on 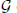f, we show that for an appropriate constant C > 0 no N ⩾ Cq½ distinct consecutive elements of such a trajectory are contained in a small subgroup of 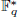, improving the trivial lower bound 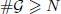. 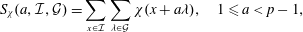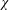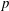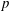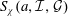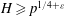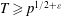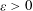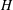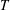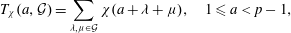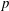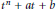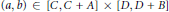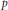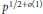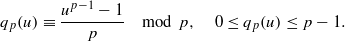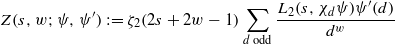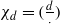Using a different technique, we also obtain a similar result for very small values of N. These results are multiplicative analogues of several recently obtained bounds on the length of intervals containing N distinct consecutive elements of such a trajectory.

We estimate double sums

$$\begin{eqnarray}S_{{\it\chi}}(a,{\mathcal{I}},{\mathcal{G}})=\mathop{\sum }\limits_{x\in {\mathcal{I}}}\mathop{\sum }\limits_{{\it\lambda}\in {\mathcal{G}}}{\it\chi}(x+a{\it\lambda}),\quad 1\leq a<p-1,\end{eqnarray}$$

${\it\chi}$

$p$

${\mathcal{I}}=\{1,\dots ,H\}$

${\mathcal{G}}$

$T$

$p$

$S_{{\it\chi}}(a,{\mathcal{I}},{\mathcal{G}})$

$H\geq p^{1/4+{\it\varepsilon}}$

$T\geq p^{1/2+{\it\varepsilon}}$

${\it\varepsilon}>0$

$H$

$T$

$$\begin{eqnarray}T_{{\it\chi}}(a,{\mathcal{G}})=\mathop{\sum }\limits_{{\it\lambda},{\it\mu}\in {\mathcal{G}}}{\it\chi}(a+{\it\lambda}+{\it\mu}),\quad 1\leq a<p-1,\end{eqnarray}$$

$p$

We give new bounds on sums of the form ∑ n≤NΛ(n)exp (2πiagn/m) and ∑ n≤NΛ(n)χ(gn+a), where Λ is the von Mangoldt function, m is a natural number, a and g are integers coprime to m, and χ is a multiplicative character modulo m. In particular, our results yield bounds on the sums ∑ p≤Nexp (2πiaMp/m) and ∑ p≤Nχ(Mp) with Mersenne numbers Mp=2p−1, where p is prime.

We obtain new results about the number of trinomials ${{t}^{n}}\,+\,at\,+\,b$ with integer coefficients in a box $(a,\,b)\,\in \,[C,\,C\,+\,A]\,\times \,[D,\,D\,+\,B]$ that are irreducible modulo a prime $p$. As a by-product we show that for any $p$ there are irreducible polynomials of height at most ${{p}^{1/2+o(1)}}$, improving on the previous estimate of ${{p}^{2/3+o(1)}}$ obtained by the author in 1989.

Given a prime p, the Fermat quotient qp(u) of u with gcd (u,p)=1 is defined by the conditions We derive a new bound on multiplicative character sums with Fermat quotients qp(ℓ) at prime arguments ℓ.

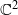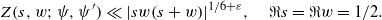
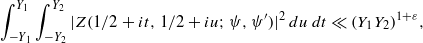
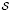For two real characters ψ,ψ′ of conductor dividing 8 define where and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to possessing a group of functional equations isomorphic to D12. The convexity bound for Z(s,w;ψ,ψ′) is |sw(s+w)|1/4+ε for ℜs=ℜw=1/2. It is proved that Moreover, the following mean square Lindelöf-type bound holds: for any Y1,Y2≥1.

Let E be an ordinary elliptic curve over a finite field q of q elements. We improve a bound on bilinear additive character sums over points on E, and obtain its analogue for bilinear multiplicative character sums. We apply these bounds to some variants of the sum-product problem on E.

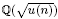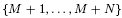Let u(n)=f(gn), where g > 1 is integer and f(X) ∈ ℤ[X] is non-constant and has no multiple roots. We use the theory of -unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among for n ∈ . Fields of this type include the Shanks fields and their generalizations.

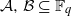Given two sets of elements of the finite field 𝔽q of q elements, we show that the product set contains an arithmetic progression of length k≥3 provided that k<p, where p is the characteristic of 𝔽q, and #𝒜#ℬ≥3q2d−2/k. We also consider geometric progressions in a shifted product set 𝒜ℬ+h, for f∈𝔽q, and obtain a similar result.

In this paper, we consider a family of elliptic curves over ${\open Q}$ with 2-torsion part ${\open Z}_2$. We prove that, for every such elliptic curve, a positive proportion of quadratic twists have Mordell–Weil rank 0.

In this paper we derive a relation between character sums and partial sums of Dirichlet series.