Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Petridis, Yiannis
Raulf, Nicole
and
Risager, Morten
2014.
Double Dirichlet series and quantum unique ergodicity of weight one-half Eisenstein series.
Algebra & Number Theory,
Vol. 8,
Issue. 7,
p.
1539.
Blomer, Valentin
Goldmakher, Leo
and
Louvel, Benoît
2014.
L-Functions with n-th-Order Twists.
International Mathematics Research Notices,
Vol. 2014,
Issue. 7,
p.
1925.
Kıral, Eren Mehmet
2015.
Subconvexity for half integral weight L-functions.
Mathematische Zeitschrift,
Vol. 281,
Issue. 3-4,
p.
689.
Dahl, Alexander
2018.
Subconvexity for a double Dirichlet series and non-vanishing of L-functions.
International Journal of Number Theory,
Vol. 14,
Issue. 06,
p.
1573.
Blomer, Valentin
2020.
EPSTEIN ZETA-FUNCTIONS, SUBCONVEXITY, AND THE PURITY CONJECTURE.
Journal of the Institute of Mathematics of Jussieu,
Vol. 19,
Issue. 2,
p.
581.
Kim, Henry H.
Tsuzuki, Masao
and
Wakatsuki, Satoshi
2022.
The Shintani double zeta functions.
Forum Mathematicum,
Vol. 34,
Issue. 2,
p.
469.
Blomer, Valentin
and
Corbett, Andrew
2022.
A symplectic restriction problem.
Mathematische Annalen,
Vol. 382,
Issue. 3-4,
p.
1323.
Čech, Martin
2023.
Mean value of real Dirichlet characters using a double Dirichlet series.
Canadian Mathematical Bulletin,
Vol. 66,
Issue. 4,
p.
1135.
Gao, Peng
and
Zhao, Liangyi
2023.
Subconvexity of a double Dirichlet series over the Gaussian field.
The Quarterly Journal of Mathematics,
Vol. 74,
Issue. 4,
p.
1237.
Gao, Peng
and
Zhao, Liangyi
2023.
First moment of central values of quadratic Hecke L-functions in the Gaussian field.
International Journal of Number Theory,
Vol. 19,
Issue. 07,
p.
1621.
Čech, Martin
2024.
The ratios conjecture for real Dirichlet characters and multiple Dirichlet series.
Transactions of the American Mathematical Society,

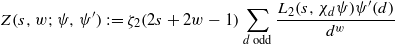
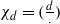 and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to
and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to 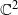 possessing a group of functional equations isomorphic to
possessing a group of functional equations isomorphic to