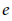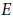Refine search
Actions for selected content:
27 results
TRIANGULATED CHARACTERIZATIONS OF SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 24 February 2025, e3
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTANCY OF THE HILBERT–SAMUEL FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 938-952
- Print publication:
- December 2024
-
- Article
- Export citation
Global Asymptotics of the Sixth Painlevé Equation in Okamoto’s Space
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 13 March 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of singularities of cluster algebras of finite type: the case of trivial coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 170-204
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Newton non-degenerate
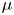 $\mu$-constant deformations admit simultaneous embedded resolutions
$\mu$-constant deformations admit simultaneous embedded resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 1268-1297
- Print publication:
- June 2022
-
- Article
- Export citation
INTERSECTION COHOMOLOGY OF RANK 2 CHARACTER VARIETIES OF SURFACE GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 08 October 2021, pp. 1615-1654
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPACE OF INITIAL VALUES OF A MAP WITH A QUARTIC INVARIANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 438-449
- Print publication:
- June 2021
-
- Article
- Export citation
Constructibilité et modération uniformes en cohomologie étale
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 19 March 2019, pp. 711-757
- Print publication:
- April 2019
-
- Article
- Export citation
COX RINGS OF MINIMAL RESOLUTIONS OF SURFACE QUOTIENT SINGULARITIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 325-355
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
Hodge Theory on Generalized Normal Crossing Varieties
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 17 December 2013, pp. 175-189
-
- Article
-
- You have access
- Export citation
G-GRAPHS AND SPECIAL REPRESENTATIONS FOR BINARY DIHEDRAL GROUPS IN GL(2,ℂ)
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 06 August 2012, pp. 23-57
- Print publication:
- January 2013
-
- Article
-
- You have access
- Export citation
ℤ[1/p]-motivic resolution of singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 01 June 2011, pp. 1434-1446
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Some Numerical Criteria for the Nash Problem on Arcs for Surfaces
-
- Journal:
- Nagoya Mathematical Journal / Volume 191 / 2008
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-19
- Print publication:
- 2008
-
- Article
-
- You have access
- Export citation
Higher Nash blowups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1493-1510
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
Ruled Exceptional Surfaces and the Poles of Motivic Zeta Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 5 / 01 October 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1098-1120
- Print publication:
- 01 October 2007
-
- Article
-
- You have access
- Export citation
Small resolutions of minuscule Schubert varieties
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 5 / September 2007
- Published online by Cambridge University Press:
- 20 September 2007, pp. 1255-1312
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
ON RATIONAL CUSPIDAL PROJECTIVE PLANE CURVES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 92 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 19 December 2005, pp. 99-138
- Print publication:
- January 2006
-
- Article
- Export citation
Three power series techniques
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 89 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 30 June 2004, pp. 1-24
- Print publication:
- July 2004
-
- Article
- Export citation
THE GLOBAL MCKAY–RUAN CORRESPONDENCE VIA MOTIVIC INTEGRATION
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 4 / July 2004
- Published online by Cambridge University Press:
- 14 June 2004, pp. 509-515
- Print publication:
- July 2004
-
- Article
- Export citation
SEIBERG–WITTEN INVARIANTS AND SURFACE SINGULARITIES. II: SINGULARITIES WITH GOOD ${\mathbb C}^*$-ACTION
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 24 May 2004, pp. 593-607
- Print publication:
- June 2004
-
- Article
- Export citation
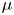

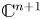
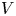
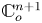

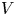
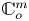
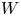
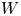
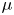
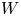
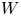
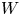
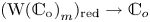
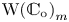
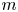
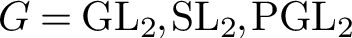
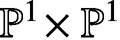
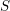
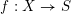
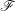
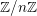
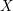
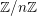
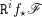
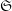
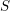
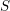
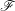
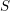
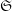
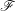
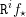
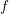
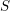
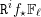
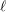
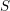
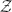
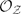
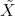 →
→ 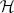 , and defines a map
, and defines a map 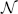 from the set of irreducible components of
from the set of irreducible components of 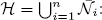
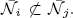 In this paper we prove that (
In this paper we prove that (