Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-31T17:36:02.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Ruled Exceptional Surfaces and the Poles of Motivic Zeta Functions

Published online by Cambridge University Press:  20 November 2018

B. Rodrigues
B. Rodrigues*
Affiliation:
Katholieke Universiteit Leuven, Departement Wiskunde, Celestijnenlaan 200B, 3001 Leuven, Belgium email: bart.rodrigues@wis.kuleuven.ac.be
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study ruled surfaces which appear as exceptional surface in a succession of blowing-ups. In particular we prove that the 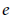$e$ -invariant of such a ruled exceptional surface 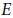$E$ is strictly positive whenever its intersection with the other exceptional surfaces does not contain a fiber (of 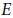$E$ ). This fact immediately enables us to resolve an open problem concerning an intersection configuration on such a ruled exceptional surface consisting of three nonintersecting sections. In the second part of the paper we apply the non-vanishing of 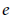$e$ to the study of the poles of the well-known topological, Hodge and motivic zeta functions.

Keywords

14E1514J2614B0514J1732S45

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 5 , 01 October 2007 , pp. 1098 - 1120
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] A’Campo, N., La fonction zêta d’une monodromie. Comment. Math. Helv. 50(1975), 233–248.Google Scholar
[2] Denef, J. and Jacobs, P., On the vanishing of principal value integrals. C. R. Acad. Sci. Paris Sér. I Math. 326(1998), no. 9, 1041–1046.Google Scholar
[3] Denef, J. and Loeser, F., Motivic Igusa zeta functions. J. Algebraic Geom. 7(1998), no. 3, 505–537.Google Scholar
[4] Hartshorne, R., Algebraic Geometry. Graduate Texts in Mathematics 52, Springer-Verlag, New York, 1977.Google Scholar
[5] Hironaka, H., Resolution of an algebraic variety over a field of characteristic zero. I, II. Ann. of Math. 79(1964), no. 2, 109–326.Google Scholar
[6] Rodrigues, B., On the geometric determination of the poles of Hodge and motivic zeta functions. J. Reine Angew. Math. 578(2005), 129–146.Google Scholar
[7] Rodrigues, B. and Veys, W., Poles of zeta functions on normal surfaces. Proc. London Math. Soc. 87(2003), no. 1, 164–196.Google Scholar
[8] Veys, W., Relations between numerical data of an embedded resolution. Amer. J. Math. 113(1991), no. 4, 573–592.Google Scholar
[9] Veys, W., Poles of Igusa's local zeta function and monodromy. Bull. Soc. Math. France 121(1993), no. 4, 545–598.Google Scholar
[10] Veys, W., Determination of the poles of the topological zeta function for curves. Manuscripta Math. 87(1995), no. 4, 435–448.Google Scholar
[11] Veys, W., Zeta functions for curves and log canonical models. Proc. London Math. Soc. 74(1997), no. 2, 360–378.Google Scholar
[12] Veys, W., Structure of rational open surfaces with non-positive Euler characteristic. Math. Ann. 312(1998), no. 3, 527–548.Google Scholar
[13] Veys, W., Vanishing of principal value integrals on surfaces. J. Reine Angew.Math. 598(2006), 139–158.Google Scholar