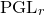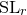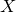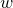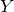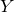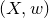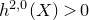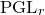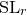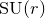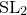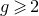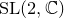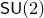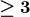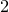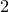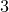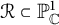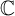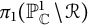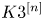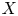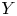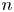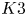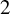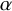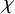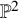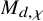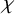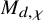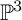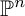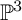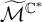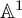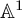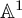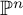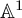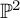Refine search
Actions for selected content:
82 results
MODULI SPACES OF SLOPE-SEMISTABLE SHEAVES WITH REFLEXIVE SESHADRI GRADUATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 22 August 2025, pp. 728-746
- Print publication:
- December 2025
-
- Article
- Export citation
Moduli spaces of rational graphically stable curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 04 August 2025, pp. 649-665
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lagrangian families of Bridgeland moduli spaces from Gushel–Mukai fourfolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 09 October 2025, pp. 2091-2135
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moduli spaces of framed logarithmic and parabolic connections on a Riemann surface
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A virtual
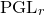 ${\rm PGL}_r$–
${\rm PGL}_r$–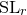 ${\rm SL}_r$ correspondence for projective surfaces
${\rm SL}_r$ correspondence for projective surfaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vector fields and admissible embeddings for quiver moduli
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On quasimap invariants of moduli spaces of Higgs bundles
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic and analytic compactifications of the Hitchin moduli space
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KSB stability is automatic in codimension
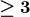 $\boldsymbol{\geq 3}$
$\boldsymbol{\geq 3}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The line bundles on the moduli stack of principal bundles on families of curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 80-127
-
- Article
- Export citation
The Atiyah class on algebraic stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 November 2024, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flags of sheaves, quivers and symmetric polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On irreducible representations of Fuchsian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 27 August 2024, pp. 970-990
- Print publication:
- December 2024
-
- Article
- Export citation
Rational Hodge isometries of hyper-Kähler varieties of
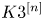 $K3^{[n]}$ type are algebraic
$K3^{[n]}$ type are algebraic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 07 May 2024, pp. 1261-1303
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic Beauville’s Conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological
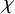 $\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on
$\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on 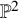 $\mathbb {P}^2$
$\mathbb {P}^2$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 01 April 2024, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NEW MODULI SPACES OF ONE-DIMENSIONAL SHEAVES ON
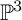 $\mathbb {P}^3$
$\mathbb {P}^3$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 265-314
- Print publication:
- June 2024
-
- Article
- Export citation
On the period of Li, Pertusi, and Zhao’s symplectic variety
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1432-1453
- Print publication:
- August 2024
-
- Article
- Export citation
INTRINSIC STABILIZER REDUCTION AND GENERALIZED DONALDSON–THOMAS INVARIANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 1987-2025
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
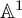 ${\mathbb A}^1$-CONNECTEDNESS OF MODULI OF VECTOR BUNDLES ON A CURVE
${\mathbb A}^1$-CONNECTEDNESS OF MODULI OF VECTOR BUNDLES ON A CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 1019-1027
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation